光学学报, 2018, 38 (12): 1229002, 网络出版: 2019-05-10
基于自相关函数重构的动态光散射偏差加权反演  下载: 904次
下载: 904次
Deviation-Weighted Inversion of Dynamic Light Scattering Based on Autocorrelation Function Reconstruction
散射 反演 粒度分布信息 自相关函数重构 信息偏差 scattering inversion particle size distribution information autocorrelation function reconstruction information deviation
摘要
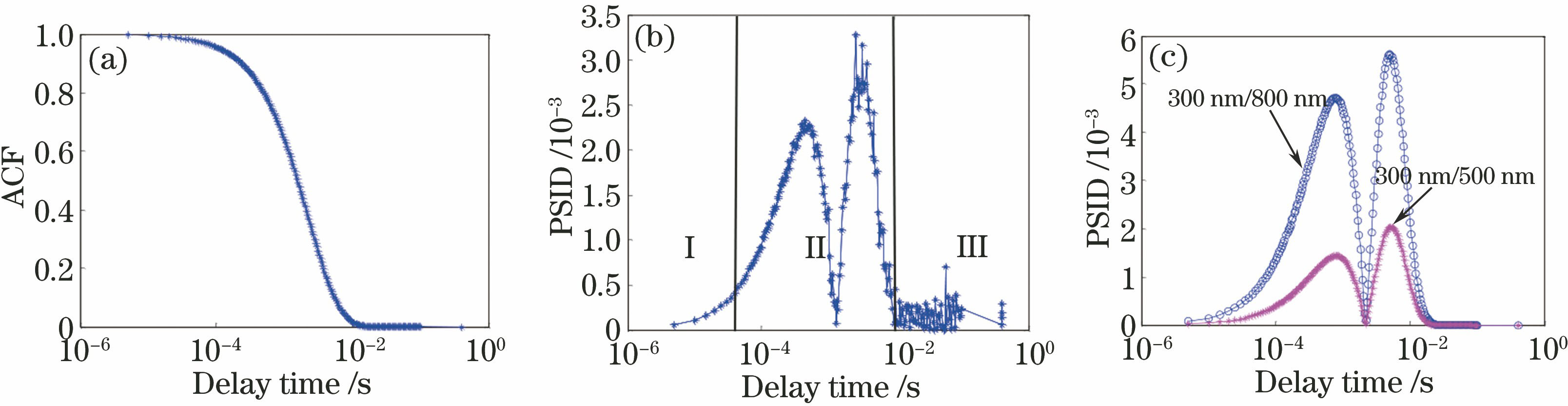
为充分利用自相关函数(ACF)衰减延迟时段的有效粒度分布信息,提出基于光强ACF重构的信息反馈式偏差加权方法,通过逐次利用偏差加权反演减小下一次偏差,直到信息偏差达到限定的最小值,即反演所得分布重构的ACF与光子相关器得到的ACF达到所要求的吻合程度。对不同噪声水平下的宽分布和近双峰分布颗粒体系模拟数据进行反演,结果表明:与常规加权反演方法相比,所提方法可以获得更准确的宽分布和近双峰分布反演结果,并具有更好的抗噪声性能。采用标准聚苯乙烯乳胶颗粒实测数据的反演结果验证了这一结论。
Abstract
An information feedback deviation-weighted method based on light intensity autocorrelation function (ACF) reconstruction is proposed to make full use of the effective particle size distribution (PSD) information in the decay section of ACF. The deviation-weighted inversion is carried out successively and the next deviation is reduced until the defined minimum information deviation is reached, that is, the distribution-reconstructed ACF obtained by inversion tends to be consistent with that obtained from the photon correlator. The inversion of the simulated data of the broad distribution and closely spaced bimodal distribution granular system at different noise levels is conducted. The results show that, compared with the routine weighting inversion methods, the proposed method can be used to obtain more accurate inversion results for the broad distribution and the closely spaced bimodal distribution and a better anti-noise performance is demonstrated, which are verified by the inversion results of the actual measurement data of standard polystyrene latex particles.
徐亚南, 申晋, 徐敏, 吴繁言, 毛帅, 王雅静, 刘伟, 孙贤明. 基于自相关函数重构的动态光散射偏差加权反演[J]. 光学学报, 2018, 38(12): 1229002. Yanan Xu, Jin Shen, Min Xu, Fanyan Wu, Shuai Mao, Yajing Wang, Wei Liu, Xianming Sun. Deviation-Weighted Inversion of Dynamic Light Scattering Based on Autocorrelation Function Reconstruction[J]. Acta Optica Sinica, 2018, 38(12): 1229002.