1 引言

随着现代光通信技术的发展,传统的光学器件已难以满足大容量、高速率的数据通信要求。波导布拉格光栅是一种基于脊状光波导制成的光栅,具有结构简单、易于制造、与互补金属氧化物半导体(CMOS)兼容等特点,广泛应用于光滤波器、光开关、光纤传感器和光学耦合器等集成光子器件中^[1-6]。作为波导的衍生器件,如何实现更高的集成度、更低的传输损耗是波导布拉格光栅目前遇到的瓶颈。表面等离激元(SPPs)作为一种存在于金属表面区域的特殊电磁波^[7],可以使光在模场尺寸上突破衍射极限,获得较长的传输距离。其中,介质/金属/介质(IMI)和金属/介质/金属(MIM)这两类对称型SPPs波导被广泛研究^[8-10]。IMI波导在光传播时具有较低的损耗,从而使得传输距离更长,因此又被称作长程表面等离激元光波导,但其横向光场偏大,导致结构无法更加紧凑。MIM波导虽然可以很好地限制光场,但由于损耗大、传输距离短,难以成为制作波导布拉格光栅的性能优异的基础器件。此外,传统的绝缘体上硅(SOI)波导的传输距离很长,被广泛用于制作波导布拉格光栅^[11-12]。然而,和IMI波导一样,SOI波导存在模场限制能力较弱的缺陷。针对上述器件存在的不足,张翔教授提出了杂化表面等离激元的波导结构^[13]。该结构的光场限制能力强,而且能大幅降低传输损耗,引起了众多研究者的关注^[14-16]。但它仍存在光被限制在金属表面而产生额外能量损耗的问题。例如,1550 nm波段下杂化表面等离激元波导的传播距离约为46.7 μm^[17]。而传输特性的优劣将直接影响波导布拉格光栅的反射滤波特性。

在此基础上,为了使光栅具有更好的反射滤波特性,针对较小的模场面积、较低的传输损耗和较长的光栅长度,本文提出了一种具有双介质层的多层波导布拉格光栅(MWBG)结构。该结构在杂化表面等离激元波导的基础上,于低折射率介质层与高折射率介质层之间添加一层折射率更低的介质层,形成狭缝波导的结构。利用三种介质之间的折射率差可以将光场进行两次压缩,形成一种独特的狭缝波导效应,使光最终被限制在折射率最低的介质层中传输,从而实现了结构的小型化。同时,由于压缩后的光场与金属之间存在一定的间距,因此降低了杂化表面等离激元波导中额外的能量损耗,使传输距离变长。此外,光栅的周期数越多,对于其滤波特性来说越好,所获得的带宽也越窄。因此,该光栅非常适合用于光滤波器、光纤传感器等集成光学器件的设计研究。

2 端面结构的设计与优化

首先针对MWBG的端面结构进行设计,并在分析过程中优化了结构参数和模场限制能力之间的关系。将x轴设定为波的传输方向,y轴和z轴分别为器件的宽度方向和高度方向。MWBG的端面结构如图1(a)所示。从图中可以看出,整个波导是一个以Ag为基底形成的多层叠加的矩形波导结构,自下而上的材料分别为SiO₂、NaF和Si。由于不同波长下的折射率会随之变化,因此该结构中的各层材料在1550 nm波长下的折射率分别为n_NaF=1.319^[18]、 n_Si=3.45、 nSiO2=1.45、n_Ag=0.1453+11.3587i^[19]。对于波导的外覆盖层,假定折射率n₀=1的空气为它的介质。此外,为了方便进行数值计算与说明,对MWBG的端面结构进行了参数定义。其中,W为整个矩形结构的宽度,H_Si为顶层Si的厚度, HSiO2和H_NaF分别为SiO₂层和NaF层的厚度。为了保证以横磁模为传输模式的电磁波在结构中传播,W设定为200 nm^[20]。在以下的设计过程中,通过COMSOL^TM软件,用有限元方法对MWBG端面结构的模态特性进行研究与分析。

图1(b)和图1(c)给出了当SiO₂层和NaF层的厚度分别为120 nm和40 nm时,1550 nm光波垂直入射到MWBG端面后,z向截面电场分量 Ez在(x=0,y=0)上的分布以及y向截面电场分量 Ey在(x=0,z=0)上的分布,右上方的插图为相应的模场图。从图中可以看出,在120 nm≤z≤160 nm和-100 nm≤y≤100 nm范围内的电场强度要高于其他范围的,说明该波导结构可以将电场

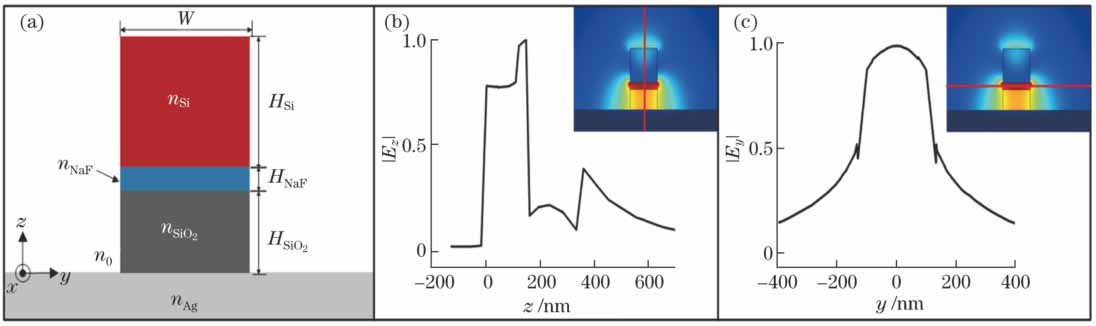
图 1. MWBG端面结构和电场分布。(a)端面结构;(b) z向的电场分布;(c) y向的电场分布

Fig. 1. End face structure of MWBG and electric field distribution. (a) Structure; (b) electric field distribution along z direction; (c) electric field distribution along y direction

下载图片 查看所有图片

限制在200 nm×40 nm的区域内,比其他SPPs波导具有更强的电场约束能力^[21]。为了更好地说明结构中的电场强度分布,通过设置归一化能量(NOP)来计算波导各层的能量与总能量的比值^[16]。电磁能量密度W(r)的表达式为^[17]:

W(r)=12Red[ωε(r)]dωE(r)2+12μ0H(r)2,(1)

式中ω为角频率,ε(r)为相对介电常数,μ₀为真空磁导率,E(r)和H(r)为传输过程中的电场和磁场强度,r为位置矢量。通过计算可知,SiO₂层、NaF层和Si层的NOP值分别为19.9%、15.8%和12.9%,说明能量主要集中在NaF层,这与模场图中的红色部分相吻合。由此说明该器件能够突破光的衍射极限,可以将光紧紧地限制在仅有几十纳米厚的NaF层内。产生这种纳米级限制能力的主要原因是该狭缝波导首先利用Si与SiO₂的高折射率差将光场限制在SiO₂层中,再利用NaF与SiO₂的折射率差对以杂化等离激元模式存在的光场进行进一步压缩,类似于顶部Si与SiO₂相互作用形成的狭缝波导效应,使能量聚集在NaF层内,增强了对模场的限制能力。

有效折射率(n_eff)是反映光传输模式的主要物理量之一,其实部Re(n_eff)表示介质对电磁波的色散,而虚部Im(n_eff)则表示传输过程中电磁波的损耗程度,根据这两个参数可以对结构性能是否优良进行评估。在SiO₂层厚度为120 nm的条件下,以10~60 nm作为NaF层厚度的变化范围,对MWBG端面的有效折射率进行分析。如图2所示,有效折射率的实部和虚部都随着H_NaF的增加呈现出下降的趋势,虚部下降得较快,从8.8073×10^-4减小到6.8492×10^-4,而实部则从1.2567减小到1.1928,下降幅度较为平缓。由此说明当NaF层厚度增加时,光波的传输损耗减小,即结构可以提供较长的传输距离。

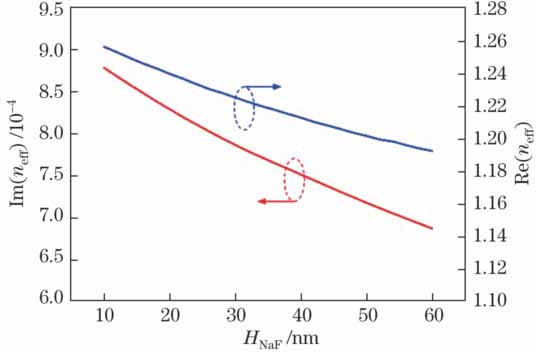
图 2. NaF层厚度与有效折射率虚部和实部的关系

Fig. 2. Relation of Re(n_eff) and Im(n_eff) with the thickness of NaF layer

下载图片 查看所有图片

为了进一步探究MWBG端面结构与模场限制能力、传输距离之间的关系,以有效折射率的虚部Im(n_eff)、传输距离L、归一化有效模场面积A_eff/A₀和品质因子α_FOM作为衡量性能的参数,对芯层中两个介质层的厚度进行研究与优化。其中,传输距离表示当电场强度降至初始值的(1/e)²时的传输距离,一般可以用公式L=λ/[4πIm(n_eff)]计算得出^[13,17]。归一化有效模场面积A_eff/A₀无纲量,其分母指的是有效模场面积(可以由A₀=λ²/4得出),分子则表示衍射极限区域的面积^[13],计算公式如下

Aeff=∫∫W(r)dA/{max[W(r)]}。(2)

此外,通过定义品质因子α_FOM可以更好地理解优化结果,其表达式为α_FOM=L/[A_eff/A₀]^[13]。可以看出,品质因子与传输长度成正比,与归一化模场面积成反比。

图3绘制了性能衡量参数与两个介质层厚度之间的关系。由图3(a)可以看到:当SiO₂层的厚度从40 nm增加到120 nm时,有效折射率的虚部逐渐变小,当NaF层的厚度分别取10,20,30,40 nm时,有效折射率虚部的变化趋势是一样的;当SiO₂层的厚度固定时,有效折射率的虚部随NaF层厚度的增加而减小。图3(b)给出了SiO₂层厚度从40 nm增加到120 nm时传输距离的变化情况,其变化趋势正好和图3(a)相反。从图3(c)可以看出:当归一化有效模场面积小于1时,器件的光场被紧紧限制在亚波长区域中;当NaF层的厚度为10,20,30,40 nm时,归一化有效模场面积随着SiO₂层厚度的增加表现为近乎线性增加。图3(d)描述了在不同NaF层厚度下,品质因子与SiO₂层厚度的变化关系,根据该图能够找到既可以把光场限制在较小区域内又能保持较长传输距离的结构。从数值上看:当SiO₂层的厚度为120 nm且NaF层的厚度为40 nm时,传输距离和归一化有效模场面积分别为178.12 μm和0.3374;当SiO₂层的厚度为40 nm且NaF层的厚度为10 nm时,传输距离和归一化有效模场面积分布达到最小值73.27 μm和0.1532。综上所述,通过对各个数值结果进行研究分析,最终可以获得一个200 nm×360 nm的最优端面结构,其中SiO₂层的厚度为120 nm,NaF层的厚度为40 nm,Si层的厚度为200 nm。在这样的最优端面结构下,传输距离

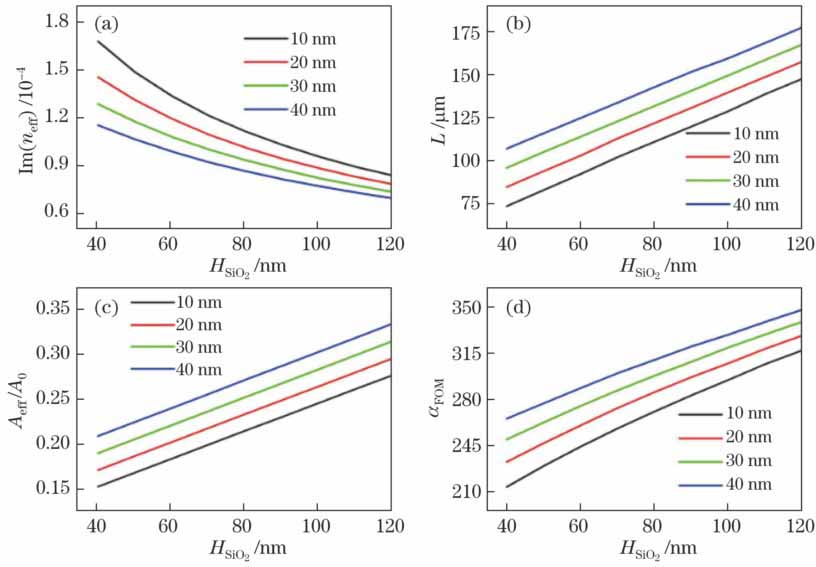
图 3. 不同NaF层厚度下,(a)有效折射率虚部、(b)传输距离、(c)归一化有效模场面积以及(d)品质因子随SiO₂层厚度的变化规律

Fig. 3. Change rule of Im(n_eff), L, A_eff/A₀ and α_FOM with thickness of SiO₂ layer at different thicknesses of NaF layer

下载图片 查看所有图片

和有效模场面积分别为178.12 μm和0.203 μm²。可以看出,在同样亚波长级的模场限制下,该结构的传输距离比同类型杂化等离激元波导的传输距离更长^{[10,16-17,22]}。

3 杂化布拉格光栅的设计与分析

第2节对MWBG的端面结构进行了设计与优化,确定了端面结构的基本尺寸,下面对MWBG进行设计与数值仿真分析。利用电子束光刻技术在Si层顶部沿x轴方向刻蚀出规则的起伏形结构(像一个个凹槽),如图4(a)所示。c和d分别表示槽的宽度和深度。周期长度作为布拉格光栅的重要参数之一,需要满足光栅的相位匹配条件^[16,23],其表达式如下:

Λ=mλc2neff=mλcneff1+neff2,(3)

式中Λ为光栅的周期长度;m为光栅的阶数;λ_c为中心波长或布拉格波长;n_eff1和n_eff2分别是光栅凹凸所在位置截面的有效折射率,它们的平均数等于端面结构的有效折射率。为了使结构更为简单,槽宽c设定为Λ/2。根据以上的研究可以发现,改变整个波导结构的高度可以影响整个结构的有效折射率。因此,为了获得光栅的周期长度,对Si层的上表面进行z轴方向上的刻蚀,刻蚀深度d设为40 nm,以得到凹凸两个截面的有效折射率。为了保证被刻蚀与未被刻蚀的整体平均尺寸与之前确定的最优端面结构尺寸一致( HSiO2=120 nm, H_NaF=40 nm和H_Si=200 nm),光栅凹槽所在部分的截面总高度为340 nm。同理,凸起截面总高度为380 nm。对凹凸截面进行数值仿真可以得知,在1550 nm波长下,二者的有效折射率分别为1.1747和1.2561。因此,通过(3)式可以计算得出周期长度为637.7 nm。这里,采用60个单元作为MWBG的周期数,可以确定沿x轴方向的光栅总长度(38.6 μm)。

通过有限时域差分法(FDTD)对光栅进行仿真分析。在仿真过程中,模式光源的波长范围为1450~1650 nm,其在光栅端面激励的模式如图1(b)所示。为了防止光波未被完全吸收而对目标波长产生影响,选择了完美匹配层(PML)作为边界吸收条件。在网格划分方面,三个坐标维度分别设置了dx=60 nm, dy=50 nm和dz=20 nm的最大网格划分。同时考虑到金属材料的特殊性,在Ag和SiO₂界面处设置了一个二次网格划分区域,其最大网格定义为dx=30 nm, dy=20 nm和dz=5 nm。经过数值模拟运算可以获得MWBG的电磁特性。在xz平面内,1550 nm波长的归一化电场分布如图4(b)所示。从图中可以发现,当光波由光栅端面进入后, 经过不断地振荡耦合,1550 nm光波被光栅反射回来。另外,传输过程中光场主要集中在NaF层传输,同样证实了MWBG对光场的亚波长限制能力。

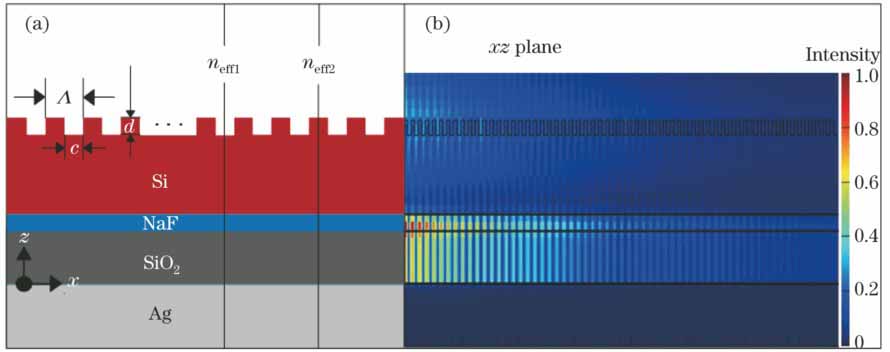
图 4. (a)xz平面内MWBG布拉格光栅结构和(b)归一化电场分布

Fig. 4. (a) Structure of MWBG Bragg grating and (b) normalized electric field distribution in xz plane

下载图片 查看所有图片

根据耦合波理论和耦合模式方程^[24-25]对光栅的反射光谱特性进一步分析。反射率R和反射光谱带宽Δλ可以由下列公式表示:

R=-iκsin(sL')γcosh(sL')+i(β-βc)sinh(sL')2,(4)s=κ2-(β-βc)2,(5)Δλ=λ2cπngκ2+(π/L')2,(6)

式中γ为失调量,κ为耦合系数,L'为光栅总长度,β和β_c分别为某一波长处的传播常数和布拉格波长处的传播常数,n_g为波导群的折射率。当耦合系数κ不变时,在布拉格波长下,光栅的反射率和反射光谱带宽与光栅的总长度相关。因此,为了更好地观察光栅的反射滤波特性,通过减少周期数制作了两个长度不同的布拉格光栅(单元数分别为30和40,相应的光栅总长度为19.36 μm和25.78 μm)。由于仅改变了周期数,所以两个光栅的耦合系数是相同的。用同样的方法来计算其反射光谱,并与所设计的布拉格光栅进行比较。如图5所示,蓝线代表60个周期数的布拉格光栅反射谱,红线代表40个周期数的布拉格光栅反射谱,黑线代表30个周期数的布拉格光栅反射谱。从图中可以看出,它们都是由中心反射区和多级旁瓣组成的,并且关于1550 nm波长的中心线对称。不同之处在于,图中蓝线的最高点即MWBG的最大反射率峰值达到了71.9%,说明所设计的光栅对1550 nm波长具有较强的反射效果,明显高于其余两个布拉格光栅(62.0%和49.2%)。该反射区域的半峰全宽(FWHM)为23.1 nm,小于另外两个布拉格光栅(28.6 nm和34.8 nm)。由此说明,光栅的总长度越长,其反射率越高,获得的带宽也越窄,反映出了良好的反射滤波特性,与耦合波理论相符合。

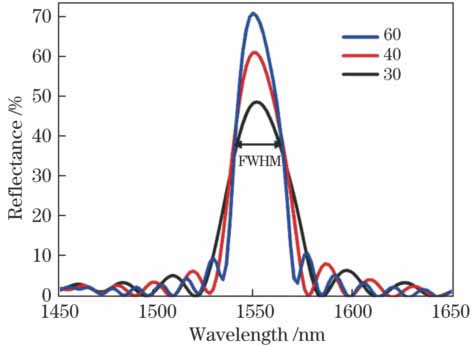
图 5. 不同周期数MWBG布拉格光栅的反射光谱

Fig. 5. Reflection spectra of MWBG Bragg grating with different cycle numbers

下载图片 查看所有图片

4 结论

提出了一种基于杂化表面等离激元的双介质层多层波导布拉格光栅。通过基于有限元方法的仿真软件对其端面结构参数进行优化,实验结果表明所提MWBG结构可以提供较强的电场约束,同时也具有相对低的传播损耗(相对于其他杂化表面等离激元波导器件,可以支持178.12 μm的传输距离)。此外,基于良好的传输性能,该MWBG在1550 nm通信波长下的反射率可以达到71.9%,并且其FWHM为23.1 nm。光栅周期数对反射滤波特性也有非常重要的影响,更多的周期数有助于提升波长的选择效果,实现更窄的带宽。该MWBG有希望成为与其他光子器件相兼容并具有实用性的光滤波器和光纤传感器。