基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建

蒋敏; 曲芝萍; 孙怡

doi:doi:10.3788/AOS201939.0711001

光学学报, 2019, 39 (7): 0711001, 网络出版: 2019-07-11

基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建下载： 1039次

Limited-Angle Computed Tomography Reconstruction Based on Mojette Minimal Redundancy Coverage in Frequency Domain

论文大纲

蒋敏曲芝萍孙怡 ^*

作者单位

大连理工大学信息与通信工程学院, 辽宁大连 116024

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

基于Mojette投影变换的空域与频域性质,提出频域最小冗余覆盖的有限角度计算机断层成像(CT)重建算法。其中频域最小冗余覆盖即空域投影采样最少,也就是重建图像的投影数目最少、效率最高。通过研究发现了Mojette投影数据在其频域上的等效关系,将投影压缩在有限角度范围内,实现了有限角度CT图像重建。实验结果表明利用所提方法可得到较好的重建结果。

Abstract

Based on the properties of Mojette projection transform in spatial and frequency domains, we propose a limited-angle computed tomography (CT)reconstruction algorithm with minimum redundancy coverage in the frequency domain. The minimum redundant coverage corresponds to the minimum spatial projection sampling (i.e., the reconstructed image has minimum number of projections with maximum efficiency). The equivalent relationship of the Mojette projection data in its frequency domain is determined. The limited-angle CT image reconstruction can be achieved by compressing the projections into a limited angular range. Experimental results show that high-quality reconstructed images can be obtained by using the proposed algorithm.

1 引言

在计算机断层成像(CT)领域中,经常遇到不完全数据重建问题,如为了降低辐射剂量采用稀疏角度采样、受扫描空间限制部分角度无法采集等。在CT成像过程中,不完全投影数据可分为两类:1)稀疏投影采样;2)有限角度投影采样。因此,针对特定CT成像问题的不同数据缺失条件,设计与之契合的重建算法,以获得满足需要的重建效果具有重要意义。除了不完全投影数据问题,直接采用近似连续Radon变换为基础的重建方法往往很难在极少角度采样的情况下获得较好的结果,因此需要寻找可以直接应用在离散域上的少角度采样重建方法。1978年Katz^[1]从离散几何的角度出发,给出了Radon变换在离散域上精确重建原信号的理论,它与1995年Herman^[2]提出的迭代算子方法共同构成了Mojette变换^[3]。由于Mojette变换基于离散几何,故可以精确重建数字化的欠采样投影,克服了Radon逆变换所带来的病态性问题。在满足Katz定理的条件下,Mojette变换能够在离散域内精确重建原信号,并能得到精确重建所需的投影方向和最少投影角度的数目。Katz定理也是目前唯一从理论上证明了能够从极少角度的离散投影数据上精确重建原数字图像的数学定理。

为了解决基于Mojette变换的不完全角度CT重建问题,2005年Servières 等^[4]从离散采样几何的角度出发,提出了共轭梯度Mojette重建算法,并通过最小二乘法实现逆问题的求解。共轭梯度Mojette重建算法在每次迭代中更新一次重建图像,但仍然需要大量的投影数据,才能保证较少的图像重建迭代次数,从而可以以更快的收敛速度获得最优解。2006年Normand等^[5]改进了从边角向中间逐步解算的传统Mojette重建算法,该方法定义了从起始点到目的地的不同重建路径,简化了重建过程,但是对投影的方向没有限定。2014年Svalbe等^[6]提出了直接反投影的重建方法,构建了一个与反投影数据相关的权重函数去规则化点扩展函数,该方法的目的是将投影的数目减少到Katz定理限制的最少投影数目。Kingston等^[7-8]基于Mojette投影数据的一维傅里叶变换,利用快速傅里叶逆变换重建图像,得到了复杂度较小的快速重建算法,并给出图像重建的一组投影集,这些投影的一维傅里叶变换能以较小的频谱冗余覆盖图像频域。2017年Jiang等^[9]提出了基于最优重建路径的Mojette重建算法,该方法在Katz定理所约束的最少投影数目的基础上,仅增加了几个投影,极大地减少了图像重建的迭代次数,但稀疏投影角度分布在[0,π]范围内。

综上,目前在基于Mojette变换的不完全角度CT重建方法中,仅有在稀疏角度情况下完成图像重建的算法。作为另一类典型的不完全数据重建问题,有限角度投影采样的缺失程度虽然不比稀疏投影采样严重,但在相等的数据采样量下,其重建的困难性远大于稀疏投影采样的重建困难性。一般地,针对稀疏角度采样问题的重建方法都可以应用到有限角度投影采样问题;然而在连续角度范围内,该方法因数据缺失,求逆问题严重病态,对采样缺失方向上重建图像信息的求解往往十分困难,因此有必要研究特定的求解策略^[10]。

本文提出基于频域最小冗余覆盖的有限角度CT重建算法。该算法首先建立Mojette投影数据的一维傅里叶变换与重建图像的二维傅里叶变换之间的映射关系,推导出Mojette变换的离散傅里叶切片定理。鉴于离散傅里叶切片位于直角坐标系下的二维傅里叶空间,本文利用基于特殊离散几何关系的频点等效方法,有效解决频域中沿切片方向分布的频点冗余的问题,同时避免了在相同频点上的重复采样。由于这种离散几何关系确定了切片方向及切片上频点分布,故本文设计了频域最小冗余覆盖方案,从覆盖频域的最优切片组合中找到空域上最优投影采集的方向,从而减少空域中的采样数量。由于离散频域的周期性,部分切片会经过相同频点,那么所对应的投影可视为等效投影,本文将最优投影矢量集等效到有限角度范围内,以实现有限角度范围内的采样。

2 离散傅里叶切片定理

傅里叶切片定理是基于Radon变换的CT系统实现断层重建的重要理论基础,它给出了Radon变换下投影数据的一维傅里叶变换与重建图像的二维傅里叶变换之间的关系,指出了投影数据的傅里叶变换可以对图像频域进行插值覆盖。傅里叶切片定理表述如下:在投影角度为θ时,重建图像f(x,y)的Radon投影数据的一维傅里叶变换(1D DFT),等于图像f(x,y)二维傅里叶变换(2D DFT)域上方向角为θ的一条直线,如图1所示。其中,R(s,θ)为在投影方向与水平方向夹角为θ时图像f(x,y)的投影,可表示为

R (s, θ) = \overset{\infty}{\int_{- \infty}} \overset{\infty}{\int_{- \infty}} f (x, y) δ (x \sin θ + y \cos θ - s) d x d y, (1)

式中:s为投影射线与探测器的交点位置,s=xcos θ+ysin θ;δ(m)为狄拉克函数,当m=0 时,δ(m)=1,其他为0。投影数据的一维傅里叶变换(1D DFT)可表示为

\begin{array}{r} R (ω, θ) = & \overset{\infty}{\int_{- \infty}} R (s, θ) \exp (- 2 πi sω) d s = \overset{\infty}{\int_{- \infty}} [\overset{\infty}{\int_{- \infty}} \overset{\infty}{\int_{- \infty}} f (x, y) δ (x \cos θ + y \sin θ - s) d x d y] \exp (- 2 πi sω) d s = \overset{\infty}{\int_{- \infty}} \overset{\infty}{\int_{- \infty}} f (x, y) [\overset{\infty}{\int_{- \infty}} δ (x \cos θ + y \sin θ - s) \exp (- 2 πi sω) d s] d x d y = \overset{\infty}{\int_{- \infty}} \overset{\infty}{\int_{- \infty}} f (x, y) \exp [- 2 πi (x \cos θ + y \sin θ) ω] d x d y = \overset{\infty}{\int_{- \infty}} \overset{\infty}{\int_{- \infty}} f (x, y) \exp [- 2 πi (xu + yv)] |_{u = ω \cos θ, v = ω \sin θ} d x d y = F (ω_{x}, ω_{y}) |_{ω_{x} = ω \cos θ, ω_{y} = ω \sin θ} 。 (2) \end{array}

式中:w_x=w·cos θ和w_y=w·sin θ分别表示水平方向和垂直方向的频率分量。从(2)式可知,投影R(s,θ)的一维傅里叶变换等于待重建图像f(x,y)的二维傅里叶变换在角度为θ的方向上的一个切线,在每个投影方向上均可向二维傅里叶平面添加一个切线。如果在[0,π]角度范围内采集足够多的投影,投影所对应的切线就能覆盖重建图像的二维傅里叶平面。

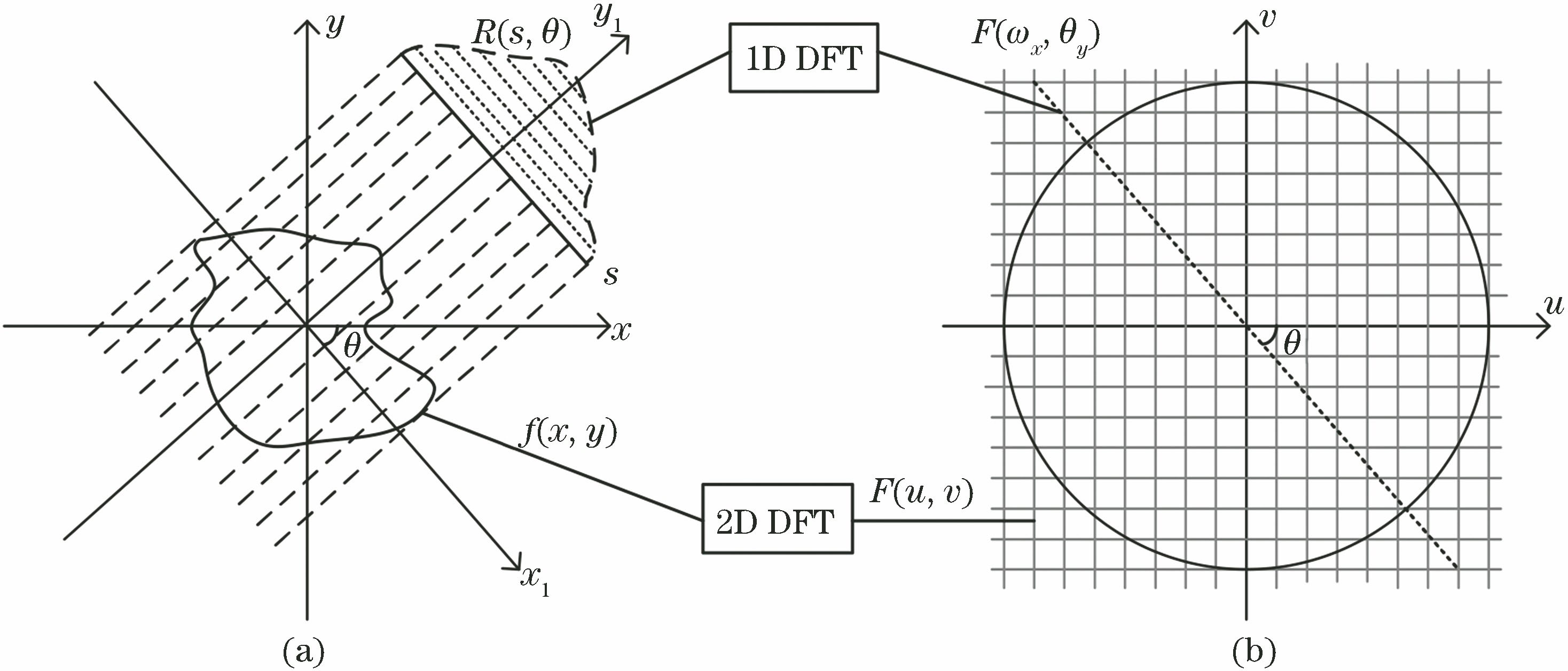
图 1. 傅里叶切片定理。(a)投影方向与水平方向夹角为θ时获得的投影R(s,θ);(b)夹角θ所对应的傅里叶切线

Fig. 1. Fourier slice theorem. (a) Projection R(s,θ) when angle between projection direction and horizontal direction is θ; (b) Fourier slice corresponding to angle θ

下载图片查看所有图片

然而,实际的CT成像系统是数字离散系统,且连续的投影模型无法适用于离散图像,因此投影获取过程中会将沿投影射线上的积分运算转换为离散求和运算。为了简化离散投影表达式中的参数,仅利用直角坐标系中X轴或Y轴参数x或y表示离散图像f(x,y),即通过投影射线所在的直线方程建立离散像素(x,y)的坐标映射关系,记为x=x;y=t+mx或x=2sy+t;y=y。其中t表示投影射线在X轴或Y轴上的截距,参数m和2s表示投影方向上平行射线斜率,m和s的表达式为

\{\begin{array}{l} 0 < m < N \\ 0 < s < N / 2 \end{array}, (3)

式中:N为正方形图像的长度或宽度。为了避免角度重叠,射线斜率m的数值范围0<m<N对应的投影角度为[π/4,π/2),射线斜率2s的数值范围0<2s<N对应的投影角度为[0,π/4)。因此,在X轴或Y轴方向存在不同的离散投影数据的表达方程。为了避免频域插值,利用傅里叶变换的离散周期性质,将离散Radon投影数据^[11]以正方形图像的长或宽N做取模运算<·>_N,即

\begin{array}{l} R (t, m) = \overset{N - 1}{\sum_{x = 0}} f (x, < t + mx >_{N}), (4) \\ R (t, 2 s) = \overset{N - 1}{\sum_{y = 0}} f (< t + 2 sy >_{N}, y) 。 (5) \end{array}

则离散周期投影数据的频域表示为

\begin{array}{r} \overset{N - 1}{\sum_{t = 0}} R (t, m) & \cdot \exp (- j \frac{2 π}{N} vt) = \overset{N - 1}{\sum_{t = 0}} \overset{N - 1}{\sum_{x = 0}} f (x, < t + mx >_{N}) \cdot \exp (- j \frac{2 π}{N} vt) = \overset{N - 1}{\sum_{x = 0}} \overset{N - 1}{\sum_{y = 0}} f (x, y) \cdot \exp [- j \frac{2 π}{N} \cdot (< - mv >_{N} \cdot x + vy)] = F (< - mv >_{N}, v), (6) \\ \overset{N - 1}{\sum_{t = 0}} R (t, 2 s) & \cdot \exp (- j \frac{2 π}{N} ut) = \overset{N - 1}{\sum_{t = 0}} \overset{N - 1}{\sum_{y = 0}} f (< t + 2 sy >_{N}, y) \cdot \exp (- j \frac{2 π}{N} ut) = \overset{N - 1}{\sum_{x = 0}} \overset{N - 1}{\sum_{y = 0}} f (x, y) \cdot \exp [- j \frac{2 π}{N} \cdot (ux + < - 2 su >_{N} \cdot y)] = F (u, < - 2 su >_{N}) 。 (7) \end{array}

因此,若已知投影射线斜率m或2s,则该投影方向上离散傅里叶切线的频点坐标可表示为(<-mv>_N,v)或(u,<-2su>_N),即离散Radon投影数据的一维傅里叶变换能映射到图像频域的一组频点上,构成图像频域的离散切线,如图2所示。

图2中用黑色虚线标记的切线斜率m=4/3,黑色虚线上的一组频点集表示沿着斜率为m=4/3射线方向的Radon投影一维傅里叶变换在图像频域上的映射;用黑色实线标记斜率s=2/3的切线,黑色实线上的一组频点集表示沿着斜率为s=2/3射线方向的Radon投影一维傅里叶变换在图像频域上的映射。

图 2. 离散傅里叶切片定理。(a)不同方向下离散Radon投影数据;(b)离散Radon投影数据的一维傅里叶变换在图像频域上的映射

Fig. 2. Discrete Fourier slice theorem. (a) Discrete Radon projection data in different angles; (b) projection of one-dimensional Fourier transform of discrete Radon projection data in Fourier domain

下载图片查看所有图片

对于离散CT成像系统,同样也存在离散傅里叶切片定理,它展示了基于离散Radon变换的投影数据的一维傅里叶变换和重建图像f(x,y)的离散二维傅里叶变换的映射关系,即投影射线斜率为m或2s的离散Radon投影的一维傅里叶变换等于f(x,y)的二维傅里叶平面上经过一组平行射线的频点集。为了减少投影采样数量并提高重建效率,本文在离散Radon变换的基础上采用了一种采样效率更高的离散Radon变换方法,即Mojette变换。

3 Mojette变换及其性质

基于Mojette变换的采样几何可以最大程度地避免像素点重复采样。类似于空域采样,在Mojette频域中同样能避免频域冗余。因此基于Mojette离散傅里叶切片定理,挑选频域最小冗余覆盖的最优切片组合,以最大程度地减少频域冗余,从而减少空域中投影采样数量。进一步地,本文找到了Mojette投影数据在其频域上的等效关系,从而将投影压缩在有限的角度范围内。

3.1 Mojette变换

Mojette变换中采用一对互质的整数(p,q)来表达投影方向,p表示图像行方向上的整数位移,q表示图像列方向上的整数位移。给定一个投影矢量(p,q),便可以计算出其所对应的投影方向θ=arctan(q/p),如图3(a)所示。基于Mojette变换方法,投影矢量(p,q)不均匀地分布于[0,π]范围内。通常情况下,K阶Mojette投影矢量集F_K={(p₁,q₁),(p₂,q₂),…,(p_k,q_k),…,|p_k|≤K,q_k≤K,k=1,2,…,K}用于界定投影方向和投影数目,它表示任意投影矢量(p_k,q_k)下的整数p_k或q_k的最大值不大于K,即|p_k|≤K,q_k≤K。例如:3阶Mojette投影矢量集为F₃={(0,1),(1,0),(1,1),(1,2),(1,3),(2,1),(2,3),(3,1),(3,2),(-1,1),(-1,2),(-1,3),(-2,1),(-2,3),(-3,1),(-3,2)},其中|p_k|≤3,q_k≤3。对于重建图像f(x,y),某个投影方向上Mojette投影数值等于平行射线上仅穿过离散像素中心的像素和,如图3(b)所示。图3(b)中给出了当投影矢量(p,q)分别为(2,1)、(1,1)和(1,0)时的Mojette投影示意图。

Mojette变换是Radon变换的一种离散形式,对分辨率大小为N×N的离散图像进行Mojette变换,其过程可表示为^[1,3]

M_{p, q} (b) = \overset{N}{\sum_{x = 1}} \overset{N}{\sum_{y = 1}} f (x, y) δ (b - px - qy), (8)

式中:f(x,y)代表待重建图像上索引坐标为(x,y)的离散像素点的灰度值;b的数值代表离散像素(x,y)经过Mojette变换后落在探测器上的像元位置。Mojette变换与Radon变换相比最大的不同在于:每个投影矢量(p,q)下所需的探测器像元数目B(N,N,p,q)不同,这也意味着在覆盖相同直径范围内的待重建图像时,不同投影角度下的投影射线之间的间距h不同,即

\{\begin{array}{l} B (N, N, p, q) = (N - 1) | p | + (N - 1) | q | + 1 \\ h = \frac{1}{\sqrt[]{p^{2} + q^{2}}} \end{array} 。 (9)

综上所述,Mojette变换通过改变不同投影矢量下投影射线的采样间隔,能够最大程度地避免一部分像素点重复和冗余采样以及另一部分像素点欠采样导致的不良效果,从而大大减小了重建断层所需的投影角度,并减少了投影射线数目。此外,Radon变换在连续域上的重建是精确的,在离散域上的重建是近似的,而Mojette变换在离散域上的重建是精确的。这两种变换的对比如表1所示。

图 3. 3×3图像的Mojette正变换示例。(a)投影矢量(p,q);(b)不同投影矢量方向上Mojette投影数据

Fig. 3. Example of Mojette transform for 3×3 image. (a) Projection vector (p,q); (b) Mojette projection data in different projection vector directions

下载图片查看所有图片

表 1. Radon变换和Mojette变换之间的差别

Table 1. Difference between Radon transform and Mojette transform

Transform method	Radon transform	Mojette transform
Difference	Fixed detector resolutionFixed angular steppingAccurate reconstruction in continuous domain, approximate reconstruction in discrete domain	Detector resolution varies with projection vectorsVariable angular steppingAccurate reconstruction in discrete domain

查看所有表

3.2 基于Mojette变换的离散傅里叶切片定理

从Radon变换和Mojette变换之间的差别可知,为了最大程度地避免像素点重复和冗余采样,可采用Mojette投影数据的一维傅里叶变换填满重建图像的频域。因为Mojette变换是一种特殊形式的离散Radon变换,离散傅里叶切片定理同样适用于Mojette变换^[12-13],即投影矢量方向为(p,q)的Mojette投影的一维傅里叶变换等于重建图像f(x,y)的二维傅里叶平面上一组平行射线穿过的频点集。Mojette投影数据的一维傅里叶变换记为

\overset{N - 1}{\sum_{b = 0}} M_{(p, q)} (b) \exp (- j \frac{2 π}{N} wb) = \overset{N - 1}{\sum_{b}} [\overset{N}{\sum_{x = 1}} \overset{N}{\sum_{y = 1}} f (x, y) δ (b - px - qy)] \exp (- j \frac{2 π}{N} wb) = \overset{N}{\sum_{x = 0}} \overset{N}{\sum_{y = 0}} f (x, y) |_{b = \mod ((px + wqy, N)} \exp (j \frac{2 π}{N} wb) = \overset{N}{\sum_{x = 0}} \overset{N}{\sum_{y = 0}} f (x, y) \exp (j \frac{2 π}{N} < wpx + wqy >_{N}) = F (< wp >_{N}, < wq >_{N}) 。 (10)

式中:mod(·)为取模运算;b为修改后探测器分辨率的长度,b=1,2,…,N;(u,v)为频域频点坐标,满足

u = < wp >_{N}, v = < wq >_{N}; w = 0,1, 2, \dots, N - 1 。 (11)

由上可知,每个Mojette投影的一维傅里叶变换包含二维傅里叶平面中的N个不同频点(u,v),每个离散傅里叶切片均是二维傅里叶空间的一组频率分量,不同方向下的傅里叶切片可以填满重建图像的二维傅里叶空间。Mojette投影数据实现频域覆盖的示意图如图4所示,其中图4(a)展示了矢量方向为(-1,1)的投影的一维傅里叶变换在二维图像频域上的切片,与此类似,图4(b)~(f)展示了其他方向投影的傅里叶变换在图像频域上的切片,这些切片叠加在一起覆盖了整个图像频域。与连续域傅里叶切片定理相同,将这些切片沿着投影方向直接放置到二维傅里叶空间中(不需要频域插值),此时可以通过离散傅里叶逆变换实现图像的重建。

图 4. 频域中不同投影方向上频点集的示意图

Fig. 4. Diagram of sets of discrete frequency points along different projection directions in Fourier domain

下载图片查看所有图片

综上所述,Mojette变换是一种特殊形式的离散Radon变换,具有离散傅里叶切片定理等重要性质。不同于极坐标系下传统频域表达方式,离散傅里叶切片位于直角坐标系下的二维傅里叶空间,它不需要插值,能避免频谱混叠现象。理论上,当投影的一维傅里叶变换映射到二维离散傅里叶空间时,对于N×N二维频域需要足够多的切片才能准确地铺满,从而获取高质量的重建图像。然而,满足图像重建的切片组合不是唯一的。因此,需要按照一些准则来覆盖二维傅里叶空间,获取满足要求的傅里叶切片组合,反推出这些切片所对应的空域投影方向,从而在CT成像时能够事先主动选择投影采集的方向。

3.3 基于Mojette频域的有限角度采样方案

Mojette变换能够在空域上最大程度地避免离散像素重复采样,减小重建断层的投影角度和减少投影射线数目。类似于空域采样,在Mojette频域中,整数对(p,q)决定了切线方向及该切线穿过的频点,因此它也能避免离散频域中频点的冗余采样。由于这种特殊的采样几何关系,在稀疏角度采样下基于Mojette频域变换的重建算法能很好地解决CT重建问题。然而,该方法目前并没有针对有限角度采样下的重建方案,而有限角度采样更适合于降低辐射剂量,如受扫描空间限制的情况。另外,本文发现不同Mojette投影提供的频点信息会重叠,甚至完全相同。因此,希望借助Mojette投影变换后的频域等效关系,将其对应的在较大范围内采样的稀疏投影压缩到有限角度范围内。

图 5. 不同投影方向上的频点。(a) θ=arctan 3的切线所经过的一组频点;(b) θ=arctan(5/7)的切线所经过的一组频点

Fig. 5. Discrete frequency points in different projection positions. (a) Frequency points along tangential corresponding to θ=arctan 3; (b) frequency points along tangential corresponding to θ=arctan(5/7)

下载图片查看所有图片

从离散频域角度出发,Du等^[14]给出了基于张量表示的离散频域的频点等效方法,借此减小图像重建所需的采样角度范围。该方法能将相同频点按照不同规律排列,形成不同方向下的切线,且切线方向由水平方向和垂直方向上整数位移p和q构成的整数对(p,q)确定。如,图5(a)表示在16×16频域中从原点沿水平方向平移p=1个频点、沿垂直方向平移q=3个频点,即沿投影方向θ=arctan 3的切线以步长 $\sqrt[]{3^{2} + 1^{2}}$ 遍历整个频域,所经过的一组频点为{(0,0),(1,3),(2,6),(3,9),(4,12),(5,15),(6,2),(7,5),(8,8),(9,11),(10,14),(11,1), (12,4),(13,7), (14,10), (15,13)}。类似地,图5(b)表示p=7和q=5时,即沿投影方向θ=arctan(5/7)的切线以步长 $\sqrt[]{7^{2} + 5^{2}}$ 遍历整个频域,得到相同频点{(0,0),(7,5),(14,10),(5,15),(12,4),(3,9),(10,14),(1,3),(8,8), (15,13), (6,2), (13,7),(4,12),(11,1),(2,6),(9,11)}。该方法使得不同方向下的切线所经过的N个频点是相同的,仅排列顺序不同。

考虑到离散频域的周期性,文献[ 14]将整数对(p,q)中的p和q分别乘以同一个奇数2n+1,然后对N进行取模运算<(2n+1)p>_N和<(2n+1)q>_N,N为二维正方形频域的长或宽,进而构建新的整数对( $\bar{p}$ , $\bar{q}$ ):

{(\bar{p}, \bar{q}) | < (2 n + 1) (p, q) >_{N}, n = 0,1, \dots, N / 2 - 1} 。 (12)

(12)式表示每对(p,q),都有一组投影{( $\bar{p}$ , $\bar{q}$ )|<(2n+1)(p,q)>_N,n=0,1,…,N/2-1}与其对应的频域切线按照不同的步长经过相同频点。此时,这些切片方向下的投影是等效的。为了减小采样角度范围,多个投影可以逐个等效到某一近邻的角度范围内,如表2所示。表2中最左边一栏为16阶Mojette投影矢量集中任意10个投影。这些投影位于0°~172.38°范围内,可以等效到90°附近的小角度范围内。以第1个投影矢量(11,1)为例,依据(12)式可获得一组投影{(1,3),(7,5),(9,11),(11,1)},其中任意2个投影能互相等效。为了使投影矢量(11,1)即投影角度5.19°更接近90°,用投影矢量(9,11)即角度为50.71°的投影等效。依此类推,原投影集将压缩到0°~104.25°有限角度范围内;类似地,也可以等效到最右边一栏48阶Mojette投影方向上,最终压缩的有限角度范围为0°~31.42°。因此,对于满足重建的傅里叶切片组合,反推出这些切片所对应的投影方向,可确保在有限角度范围内采样。本文从频域出发,设计最小冗余覆盖二维频域空间的重建图像准则,进而利用上述等效关系将重建图像的采样范围压缩到有限角度内。

表 2. 任意10个投影等效后的角度范围

Table 2. Angular ranges of ten equivalent projections

Angular range of 172.38°		Equivalent angular range of 104.25°		Equivalent angular range of 31.42°
(16-order sets of Mojette projections)		(16-order sets of Mojette projections)		(48-order sets of Mojette projections)
Projection vector	Angle /(°)	Equivalent projection vector	Equivalent projection angle /(°)	Equivalent projection vector	Equivalent projection angle /(°)
(11,1)			5.19			(9,11)	50.71	(1,3)	71.57
(15,1)			3.81			(9,7)	37.88	(3,13)	77.01
(11,5)			24.43			(7,9)	52.13	(7,41)	80.31
(9,7)			37.87			(5,11)	65.56	(5,43)	83.37
(1,15)			86.19			(1,15)	86.19	(1,47)	88.78
(-1,15)			93.81			(-1,15)	93.81	(-1,47)	91.22
(-5,11)			114.44			(-3,13)	103.00	(-1,15)	93.81
(-9,7)			142.13			(-5,11)	114.45	(-5,43)	96.63
(-13,3)			167.01			(-7,9)	127.88	(-7,41)	99.69
(-15,1)			176.19			(-9,7)	142.13	(-3,13)	102.99

查看所有表

3.4 Mojette频域最小冗余覆盖方案

3.3节从频域的角度出发挑选空域中的投影,为减小空域采样,需要最大程度地减小频域冗余,因此本节将提出Mojette频域最小冗余覆盖方案。由于覆盖频域的每个切片均包含N个频点,为确保覆盖N×N二维频域需要的切片数目尽量少,所有被挑选切片之间的频点应尽量少地重叠,从而找到频域最小冗余覆盖的最优切片组合。因此,在逐个挑选切片的过程中,应保证当前被挑选切片上的频点能够覆盖到最多的未被挑选到的频点。

由于图像轮廓信息主要集中在低频区域,本文更注重低频区域内的频点覆盖情况。在N×N二维频域中,界定低频区域的频点范围为{(u,v)|N/4<u<3N/4,N/4<v<{(u,v)|N/4<u<3N/4},其中频域坐标中心位于(N/2+1,N/2+1)处。按照频域最小冗余覆盖挑选傅里叶切片的过程如下:在当前挑选频域切片的过程中,选择低频区域内频点数目最多的切片,实现部分频域空间覆盖。通常,不止一个切片满足条件,依据(12)式找到与切片具有频域等效关系的一组投影,选择包含投影数最多的一组投影所对应的切片,这意味着投影等效时有更多选择,有利于压缩角度范围;接着,将当前被选中切片所经频点移除,即每挑选一个切片后都要更新一次频域内的频点信息;重复上述步骤,直至不同切片上频点的组合最小冗余地覆盖图像频域,此时所需切片对应的投影数目也是最少的。被挑选切片上频点数目最多,即被挑选的切片能提供的频点信息最多,从而实现覆盖整个N×N频域空间所需切片的数目最少。

综上所述,通过Mojette变换将图像信息映射到投影域,再从投影域转换到频域,需要足够多个切片覆盖整个频域。采用这种基于特殊离散几何的频点组合方法确定最优切片组合,以实现图像频域最小冗余覆盖,从而确定了图像重建的最优投影矢量集,并实现空域中采样数目最少。为了减小空域中的采样角度范围,对于最优投影矢量集,可以按照(12)式计算各投影矢量的等效角度,进而将最优投影矢量集等效到某一角度附近的有限角度范围内。

4 基于Mojette频域的有限角CT重建算法

Mojette变换是一种最小冗余采样的离散Radon变换,在离散图像域转换到投影域的过程中,可以主动选择投影方向,同时避免像素点的重复采样。此外,由离散傅里叶切片定理可知,Mojette投影的傅里叶切片分布在直角坐标系下的二维频域,不需要频域插值,可避免频谱混叠现象。当借助Mojette投影数据从频域重建图像时,本文没有采用以解决频点混叠问题为主的傅里叶逆变换算法,而是应用从高度不完备信息中恢复信号的压缩感知(CS)理论^[15],利用部分频谱信息完成图像重建,更加适合有限角度下的Mojette频域重建。综上所述,所提基于Mojette频域的有限角CT重建算法流程如下:

1) 用K阶Mojette投影矢量集F_K表示图像重建的投影方向和投影数目,阶数K越大,包含投影的数目越多,(12)式中能互相等效的投影越多。

2) 获得Mojette投影数据的频域傅里叶变换。

3) 按照Mojette频域最小冗余覆盖方案,对K阶投影矢量集按照3.4节所述方法进行优选,得到最优投影矢量集,其中频域覆盖冗余最小相当于重建所需投影角度数量最少。

4) 对于投影矢量(p,q),按照3.3节中所述方案找到一组投影{( $\bar{p}$ , $\bar{q}$ )|<(2n+1)(p,q)>_N},它们的切片能提供相同的频点信息,这些投影可以互相等效。

5) 为了减小空域中采样角度的范围,按照步骤4)将投影等效映射,使得映射后的最优投影矢量集分布在有限角度范围内。

6) 利用傅里叶系数压缩感知重建算法重构原始图像^[15],将有限角度内的投影数据映射到二维频域,作为压缩感知中频域一致性的约束项,重构算法采用交替方向乘子法优化求解:

\min_{x} TV (f) + λ ‖Ψ f ‖_{1} + μ ‖ F_{j} - T_{j} ‖^{2}, (13)

式中:‖‖₁为l₁范数,表示向量中各个元素绝对值之和;f为待重建图像;TV(·)为总变分正则项;ψ为稀疏表达基,这里采用小波基作为稀疏表达基; F_j为部分傅里叶矩阵;T_j为感知矩阵,j表示选择矩阵的j行。该压缩感知重建算法减少了恢复图像所需的傅里叶采样数据量,适用于基于Mojette频域的有限角度CT重建。

本文从频域的角度出发选择投影方向,首先按照频域最小冗余覆盖方案挑选最优投影矢量集,能够有效减少投影数目;然后,将最优投影矢量集等效到有限角度范围内,从而减小空域中采样角度范围,实现在有限角度范围内CT图像的重建。

5 实验结果及分析

所提算法从频域出发,以频域最小冗余覆盖为标准挑选切片,利用Mojette频域性质压缩空域中的角度范围,求解目标函数重构图像。通过仿真实验,本节验证了频域最小冗余覆盖方案的有效性及所提算法的重建性能。此外,将所提算法与其他基于频域的有限角CT重建算法和联合代数重建算法(SART)进行了对比,证明利用所提算法可以获得精确的重建结果。

首先,在用最少数目的切片覆盖图像频域情况下验证所提算法的重建性能。为了将图像重建所需的最优投影集等效到有限角度范围内,对集合中的每个投影矢量(p,q),按照3.3节找到一组投影{( $\bar{p}$ , $\bar{q}$ )|<(2n+1)(p,q)>_N},它应该包含足够多的投影数目,即能互相等效的投影角度足够多。统计数据表明:对于重建尺寸为64 pixel×64 pixel的图像,64阶Mojette投影矢量集F₆₄能满足上述要求。依据所提重建算法流程,先将64阶Mojette投影矢量集F₆₄中投影数据的一维傅里叶变换映射到图像频域;按照频域最小冗余覆盖方案挑选出87个投影,这些投影非均匀地分布在[0,π]范围内;找到每个投影方向在空域中对应的一组等效投影{( $\bar{p}$ , $\bar{q}$ )|<(2n+1)(p,q)>_N};考虑到投影矢量( $\bar{p}$ , $\bar{q}$ )中 $\bar{p}$ 为正数或负数,即投影角度θ=arctan( $\bar{q}$ / $\bar{p}$ )分布在[0,π/2]或(π/2,π]范围内,为使压缩后的角度范围较小,将这87个投影分别等效到离90°最近的角度上,最终分布在[82.76°,97.24°]有限角度范围内。随后,将有限角度下投影数据的一维傅里叶变换映射到图像的二维傅里叶空间并输入到目标函数中,求解(13)式优化问题,获得的重建结果如图6所示。图6(a)~(d)为原始图像;图6(e)~(h)为重建图像的二维傅里叶域的覆盖情况,框中区域表示图像频域的低频区域,它集中了图像轮廓的主要信息;图6(i)~(l)为所提算法获得的重建结果。由图6可知,所提算法改善了有限角度范围内较少采样数据导致的重建伪影,可获得高质量的重建结果。

图 6. 所提算法的重建结果。(a)~(d)原始图像;(e)~(h)重建图像的二维频域;(i)~(l)所提算法的重建结果

Fig. 6. Reconstruction results of proposed algorithm. (a)-(d) Original images; (e)-(h) two-dimensional frequency domain of reconstruction images; (i)-(l) reconstruction results of proposed algorithm

下载图片查看所有图片

进一步通过对比实验来证明所提算法的准确性和有效性。对比算法包括文献[ 14]中基于张量表示的有限角CT重建算法和联合代数重建算法SART。为了在相同实验环境中与两种算法进行对比,本文同样采用文献[ 14]中有限角CT重建算法所给出的原始图像进行重建,采样条件如表3所示,实验结果如图7所示。图7(a)(e)(i)是尺寸为256 pixel×256 pixel的原始图像,图7(b)(f)(j)是文献[ 14]中的重建结果,该方法利用频域中一些切片经过相同频点的思想,将填满图像频域的各个切片所对应的投影等效到有限角度范围。获取有限角度范围的投影数据之后,将投影数据直接一一映射到离散图像域的像素上,完成直接反投影重建。该方法采用了384个投影,投影角度分布在[0°,10°]范围。图7(c)(g)(k)是所提算法的重建结果,采用18个投影,投影角度分布在[86.37°,94.01°]范围。类似地,联合代数重建算法SART利用[86.37°,94.01°]范围内的18个均匀投影重建图像,重建结果如图7(d)(h)(l)所示。

表 3. 几种算法的扫描参数区别

Table 3. Comparison of scanning parameters for several algorithms

Algorithm	Proposed algorithm	Literature [14]	SART
Reconstruction results	Figs. 6(c)(g)(k)	Figs. 6(b)(f)(j)	Figs. 6(d)(h)(l)
Angular range	[86.37°,94.01°]	[0°,10°]	[86.37°,94.01°]
Number of projections	18	384	18

查看所有表

图8展示了图7中三个重建结果沿水平方向的28行切面上像素灰度值的变化曲线,可以看出:所提算法的重建结果与原始图像的像素灰度值完全一致,实现了对原始图像的精确重建。从图8可知,所提算法利用有限角度下的少数投影数据获得了更高质量的重建结果,明显改善了文献[ 14]中重建结果的竖条纹伪影现象。此外,SART算法虽然能获得高质量的重建结果,但仅是对原始图像的近似重建。

图 7. 几种算法的重建结果对比。(a)(e)(i)原始图像;(b)(f)(j)文献[ 14]中的重建结果;(c)(g)(k)所提算法的重建结果;(d)(h)(l) SART算法的重建结果

Fig. 7. Comparison of reconstruction results of several algorithms. (a)(e)(i) Original images; (b)(f)(j) reconstruction results in Ref. [14]; (c)(g)(k) reconstruction results of proposed algorithm; (d)(h)(l) reconstruction results of SART algorithm

下载图片查看所有图片

图 8. 水平方向28行切面上像素灰度值的变化曲线。(a)图7中第1排图像灰度值;(b)图7中第2排图像灰度值;(c)图7中第3排图像灰度值

Fig. 8. Image gray values in 28-th row of images in horizontal directions. (a) Image gray value in 1st row of Fig. 7; (b) image gray value in 2nd row of Fig. 7; (c) image gray value in 3rd row of Fig. 7

下载图片查看所有图片

表4给出了利用所提算法和SART算法获得的重建结果的结构相似度(SSIM)和峰值信噪比(PSNR)。因文献[ 14]中的重建结果伪影比较严重,且文献[ 14]中的算法需要的投影数目是所提算法的20倍,所以表4没有列出该重建结果的SSIM和PSNR。通过对比实验结果可以发现:所提算法能够获得与原始图像几乎一样的重建结果。此外,从离散几何出发的Mojette精确重建算法在较小的噪声干扰下能取得优异的性能。然而,当噪声增大时,由于精确重建方法对噪声较为敏感,性能变差,因此其重建结果比基于l₀正则化重建方法^[16]差。

表 4. 对比实验结果的量化指标

Table 4. Quantitative indicators for comparison results

Result
Original image in Fig. 7(a)	Mojette result in Fig. 7(c)	0.9803	28.53
Original image in Fig. 7(a)	SART result in Fig. 7(d)	0.9445	28.34
Original image in Fig. 7(e)	Mojette result in Fig. 7(g)	1.0000	>50.00
Original image in Fig. 7(e)	SART result in Fig. 7(h)	0.9419	34.73
Original image in Fig. 7(i)	Mojette result in Fig. 7(k)	1.0000	>50.00
Original image in Fig. 7(i)	SART result in Fig. 7(l)	0.9337	36.13

查看所有表

6 结论

提出了基于Mojette频域最小冗余覆盖的有限角CT重建算法,按照频域最小冗余覆盖方案选取图像重建所需的最优投影矢量集。将这些投影数据的傅里叶变换映射到重建图像的二维傅里叶空间,不仅能无插值覆盖频域,避免了插值误差对重建结果的影响,而且可以有效减少频点冗余,提高算法的重建性能。采用基于压缩感知的重建算法可减少图像精确重建所需的傅里叶采样数据量,从而改善有限角度范围内较少采样数据所导致的重建伪影。

参考文献

[1] Katz MB. Questions of uniqueness and resolution in reconstruction from projections[M]. Berlin, Heidelberg: Springer, 1978.

[2] Herman GT. Image reconstruction from projections implementation and applications[M]. New York: Springer-Verlag, 1979.

[3] Guédon J V, Barba D, Burger N. Psychovisual image coding via an exact discrete Radon transform[J]. Proceedings of SPIE, 1995, 2501: 562-572.

[4] Servières M, Idier J, Normand N, et al. Conjugate gradient Mojette reconstruction[J]. Proceedings of SPIE, 2005, 5747: 2067-2075.

[5] NormandN, KingstonA, ÉvenouP. A geometry driven reconstruction algorithm for the Mojette transform[M] //Kuba A, Nyúl L G, Palágyi K. Discrete geometry for computer imagery. Lecture notes in computer science. Berlin, Heidelberg: Springer, 2006, 4245: 122- 133.

[6] SvalbeI, KingstonA, NormandN, et al. Back-Projection filtration inversion of discrete projections[M] //Barcucci E, Frosini A, Rinaldi S. Advanced information systems engineering. Berlin, Heidelberg: Springer, 2014: 238- 249.

[7] KingstonA, HeyangL, NormandN, et al. Fourier inversion of the Mojette transform[M] //Barcucci E, Frosini A, Rinaldi S. Discrete geometry for computer imagery. Lecture notes in computer science. Cham: Springer, 2014, 8668: 275- 284.

[8] Thriveni T, Bharati K F. Digital image reconstruction through its projected views by using Discrete Fourier Slice Theorem[J]. International Research Journal of Engineering and Technology, 2015, 2(4): 1040-1044.

[9] Jiang M, Sun Y, Qu Z P, et al. Priority-based Mojette reconstruction from sparse noisy projections[J]. Journal of X-Ray Science and Technology, 2017, 25(6): 993-1006.

[10] 张瀚铭. CT不完全数据重建算法研究[D]. 郑州: 解放军信息工程大学, 2017: 13- 15.

Zhang HM. Computed tomography image reconstruction with incomplete projection data[D]. Zhengzhou: PLA Information Engineering University, 2017: 13- 15.

[11] Hsung T C. Lun D P K, Siu W C. The discrete periodic Radon transform[J]. IEEE Transactions on Signal Processing, 1996, 44(10): 2651-2657.

[12] Hou W, Zhang C S. Parallel-beam CT reconstruction based on Mojette transform and compressed sensing[J]. International Journal of Computer and Electrical Engineering, 2013: 83-87.

[13] Chandra S S, Normand N, Kingston A, et al. Robust digital image reconstruction via the discrete Fourier slice theorem[J]. IEEE Signal Processing Letters, 2014, 21(6): 682-686.

[14] Du N, Feng Y S, Grigoryan A M. Image reconstruction from limited-angle range projections[J]. Proceedings of SPIE, 2013, 8668: 86683I.

[15] Yang JF, ZhangY, Yin W T. A fast TVL1-L2 minimization algorithm for signal reconstruction from partial Fourier data[R]. ( 2008-10)[2019-01-01]. https://scholarship.rice.edu/handle/1911/102105.

[16] Zeng L, Wang C X. Error bounds and stability in the l0 regularized for CT reconstruction from small projections[J]. Inverse Problems and Imaging, 2016, 10(3): 829-853.

3.2 基于Mojette变换的离散傅里叶切片定理

3.3 基于Mojette频域的有限角度采样方案

3.4 Mojette频域最小冗余覆盖方案

4 基于Mojette频域的有限角CT重建算法

5 实验结果及分析

6 结论

蒋敏, 曲芝萍, 孙怡. 基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建[J]. 光学学报, 2019, 39(7): 0711001. Min Jiang, Zhiping Qu, Yi Sun. Limited-Angle Computed Tomography Reconstruction Based on Mojette Minimal Redundancy Coverage in Frequency Domain[J]. Acta Optica Sinica, 2019, 39(7): 0711001.

基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建下载： 1039次

1 引言

2 离散傅里叶切片定理

图 1. 傅里叶切片定理。(a)投影方向与水平方向夹角为θ时获得的投影R(s,θ);(b)夹角θ所对应的傅里叶切线

Fig. 1. Fourier slice theorem. (a) Projection R(s,θ) when angle between projection direction and horizontal direction is θ; (b) Fourier slice corresponding to angle θ

图 2. 离散傅里叶切片定理。(a)不同方向下离散Radon投影数据;(b)离散Radon投影数据的一维傅里叶变换在图像频域上的映射

Fig. 2. Discrete Fourier slice theorem. (a) Discrete Radon projection data in different angles; (b) projection of one-dimensional Fourier transform of discrete Radon projection data in Fourier domain

3 Mojette变换及其性质

3.1 Mojette变换

图 3. 3×3图像的Mojette正变换示例。(a)投影矢量(p,q);(b)不同投影矢量方向上Mojette投影数据

Fig. 3. Example of Mojette transform for 3×3 image. (a) Projection vector (p,q); (b) Mojette projection data in different projection vector directions

表 1. Radon变换和Mojette变换之间的差别

Table 1. Difference between Radon transform and Mojette transform

3.2 基于Mojette变换的离散傅里叶切片定理

图 4. 频域中不同投影方向上频点集的示意图

Fig. 4. Diagram of sets of discrete frequency points along different projection directions in Fourier domain

3.3 基于Mojette频域的有限角度采样方案

图 5. 不同投影方向上的频点。(a) θ=arctan 3的切线所经过的一组频点;(b) θ=arctan(5/7)的切线所经过的一组频点

Fig. 5. Discrete frequency points in different projection positions. (a) Frequency points along tangential corresponding to θ=arctan 3; (b) frequency points along tangential corresponding to θ=arctan(5/7)

表 2. 任意10个投影等效后的角度范围

Table 2. Angular ranges of ten equivalent projections

3.4 Mojette频域最小冗余覆盖方案

4 基于Mojette频域的有限角CT重建算法

5 实验结果及分析

图 6. 所提算法的重建结果。(a)~(d)原始图像;(e)~(h)重建图像的二维频域;(i)~(l)所提算法的重建结果

Fig. 6. Reconstruction results of proposed algorithm. (a)-(d) Original images; (e)-(h) two-dimensional frequency domain of reconstruction images; (i)-(l) reconstruction results of proposed algorithm

表 3. 几种算法的扫描参数区别

Table 3. Comparison of scanning parameters for several algorithms

图 7. 几种算法的重建结果对比。(a)(e)(i)原始图像;(b)(f)(j)文献[ 14]中的重建结果;(c)(g)(k)所提算法的重建结果;(d)(h)(l) SART算法的重建结果

Fig. 7. Comparison of reconstruction results of several algorithms. (a)(e)(i) Original images; (b)(f)(j) reconstruction results in Ref. [14]; (c)(g)(k) reconstruction results of proposed algorithm; (d)(h)(l) reconstruction results of SART algorithm

图 8. 水平方向28行切面上像素灰度值的变化曲线。(a)图7中第1排图像灰度值;(b)图7中第2排图像灰度值;(c)图7中第3排图像灰度值

Fig. 8. Image gray values in 28-th row of images in horizontal directions. (a) Image gray value in 1st row of Fig. 7; (b) image gray value in 2nd row of Fig. 7; (c) image gray value in 3rd row of Fig. 7

表 4. 对比实验结果的量化指标

Table 4. Quantitative indicators for comparison results

6 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建 下载： 1039次

1 引言

2 离散傅里叶切片定理

图 1. 傅里叶切片定理。(a)投影方向与水平方向夹角为θ时获得的投影R(s,θ);(b)夹角θ所对应的傅里叶切线

Fig. 1. Fourier slice theorem. (a) Projection R(s,θ) when angle between projection direction and horizontal direction is θ; (b) Fourier slice corresponding to angle θ

图 2. 离散傅里叶切片定理。(a)不同方向下离散Radon投影数据;(b)离散Radon投影数据的一维傅里叶变换在图像频域上的映射

Fig. 2. Discrete Fourier slice theorem. (a) Discrete Radon projection data in different angles; (b) projection of one-dimensional Fourier transform of discrete Radon projection data in Fourier domain

3 Mojette变换及其性质

3.1 Mojette变换

图 3. 3×3图像的Mojette正变换示例。(a)投影矢量(p,q);(b)不同投影矢量方向上Mojette投影数据

Fig. 3. Example of Mojette transform for 3×3 image. (a) Projection vector (p,q); (b) Mojette projection data in different projection vector directions

表 1. Radon变换和Mojette变换之间的差别

Table 1. Difference between Radon transform and Mojette transform

3.2 基于Mojette变换的离散傅里叶切片定理

图 4. 频域中不同投影方向上频点集的示意图

Fig. 4. Diagram of sets of discrete frequency points along different projection directions in Fourier domain

3.3 基于Mojette频域的有限角度采样方案

图 5. 不同投影方向上的频点。(a) θ=arctan 3的切线所经过的一组频点;(b) θ=arctan(5/7)的切线所经过的一组频点

Fig. 5. Discrete frequency points in different projection positions. (a) Frequency points along tangential corresponding to θ=arctan 3; (b) frequency points along tangential corresponding to θ=arctan(5/7)

表 2. 任意10个投影等效后的角度范围

Table 2. Angular ranges of ten equivalent projections

3.4 Mojette频域最小冗余覆盖方案

4 基于Mojette频域的有限角CT重建算法

5 实验结果及分析

图 6. 所提算法的重建结果。(a)~(d)原始图像;(e)~(h)重建图像的二维频域;(i)~(l)所提算法的重建结果

Fig. 6. Reconstruction results of proposed algorithm. (a)-(d) Original images; (e)-(h) two-dimensional frequency domain of reconstruction images; (i)-(l) reconstruction results of proposed algorithm

表 3. 几种算法的扫描参数区别

Table 3. Comparison of scanning parameters for several algorithms

图 7. 几种算法的重建结果对比。(a)(e)(i)原始图像;(b)(f)(j)文献[ 14]中的重建结果;(c)(g)(k)所提算法的重建结果;(d)(h)(l) SART算法的重建结果

Fig. 7. Comparison of reconstruction results of several algorithms. (a)(e)(i) Original images; (b)(f)(j) reconstruction results in Ref. [14]; (c)(g)(k) reconstruction results of proposed algorithm; (d)(h)(l) reconstruction results of SART algorithm

图 8. 水平方向28行切面上像素灰度值的变化曲线。(a)图7中第1排图像灰度值;(b)图7中第2排图像灰度值;(c)图7中第3排图像灰度值

Fig. 8. Image gray values in 28-th row of images in horizontal directions. (a) Image gray value in 1st row of Fig. 7; (b) image gray value in 2nd row of Fig. 7; (c) image gray value in 3rd row of Fig. 7

表 4. 对比实验结果的量化指标

Table 4. Quantitative indicators for comparison results

6 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于Mojette频域最小冗余覆盖的有限角度计算机层析成像重建下载： 1039次