基于Jeffrey散度相似性度量的加权FCM聚类算法

吴辰文; 马宁; 蒋雨璠

doi:doi:10.3788/LOP202158.0810006

激光与光电子学进展, 2021, 58 (8): 0810006, 网络出版: 2021-04-06

基于Jeffrey散度相似性度量的加权FCM聚类算法下载： 828次

Weighted FCM Clustering Algorithm Based on Jeffrey Divergence Similarity Measure

论文大纲

吴辰文马宁 ^*蒋雨璠

作者单位

兰州交通大学电子与信息工程学院, 甘肃兰州 730070

图像处理聚类算法加权模糊C均值算法 Jeffrey散度 image processing clustering algorithm weighted fuzzy C means algorithm Jeffrey divergence

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

针对模糊C均值(FCM)聚类算法在数据集下聚类效果差的情况,以及基于欧氏距离的相似性度量只考虑数据点之间的局部一致性问题,提出了基于Jeffery散度相似性度量加权FCM聚类算法(JW-FCM)。引入源于Jeffery散度的相似性度量,首先,对于FCM算法进行特征加权,对数据的不同特征值赋予适当的权重,再将Jeffery散度与加权FCM算法进行结合得到JW-FCM算法。将JW-FCM算法与几种相关算法在人工数据集和UCI数据集上进行对比实验,通过实验分析与比较,证明了JW-FCM算法具有更好的收敛性、鲁棒性、准确性。实验结果表明,改进算法表现出较好的聚类效果。

Abstract

In view of the poor clustering effect of the fuzzy C mean (FCM) clustering algorithm under the data set, and the similarity measure based on Euclidean distance only considers the local consistency between data points. This paper presents a weighted FCM clustering algorithm based on Jeffrey divergence similarity measure (JW-FCM), and introduces the similarity measure derived from Jeffery divergence. First, perform feature weighting on the FCM algorithm, assign appropriate weights to different feature values of the data, and then combine the Jeffery divergence with the weighted FCM algorithm to obtain the JW-FCM algorithm. The JW-FCM algorithm is compared with several related algorithms on the artificial data set and UCI data set. Through experimental analysis and comparison, it is proved that the JW-FCM algorithm has better convergence, robustness, and accuracy. The experimental results show that the improved algorithm shows better clustering effect.

1 引言

聚类是模式识别领域的一个重要的研究方向^[1],它是基于某些预先固定的相同或不相同的度量来寻找有意义组的方法,在统计数据分析中被广泛应用^[2]。聚类在有效的数据分析过程中起着关键作用,它从原始数据集提取必要信息和粒度信息(指信息单元的相对大小或粗糙程度)。与监督学习和判别分析不同,它不涉及标记数据或训练集。在数据挖掘、信息检索、机器学习和计算机视觉等领域,聚类分析是一项核心技术。已有大量研究基于不同的假设(如连通性、形心、分布、密度和子空间等)提出了多个聚类算法。由于不同的算法会获得不同的效果,因此很难在实践中确定使用哪种算法^[3]。经典算法有K-means^[4]、模糊C均值(FCM)^[5]、DBSCAN^[6]等。

然而,现如今的聚类算法基本上还存在一些问题:1)聚类结果可能是局部最优解,例如K-means聚类算法类似于爬山法,会在最近的最优点停止迭代,但是这个最优点不一定是全局的最优点;2)聚类过程中容易受到噪声和环境因素的影响等,因此聚类结果比较依赖于相似性度量。一般来说,在聚类算法中,欧氏相似性度量经常被用来最小化每个点到其最近中心的均方距离。欧氏距离不能总是找到更精确的聚类边界,本研究采用加权的FCM聚类方法作为衡量相似性度量方法的基础算法。近年来,研究者们利用非线性相似性度量代替传统的欧氏距离来确定更精确的聚类边界,相对较为熟悉的是三角不等式性质^[7]。Banerjee等^[8]在2005年使用广义Bregman散度作为一种相似性度量方法与K-means方法进行结合,改进了传统K-means方法的性能。

在目前的模糊聚类算法研究中,FCM聚类算法有较为完善的理论基础,同时FCM算法能计算样本对所有类的隶属度,提供了参考该样本结果可靠性的计算方式。但是FCM聚类算法仍然存在如下缺点: 1)FCM算法是一种有效的图像分割算法,但对噪声图像分割效果较差^[9];2)加权指数b的选取;3)目标函数中相似性度量的定义等。因此不仅需要去探究与解决其聚类结果不稳定性及噪声敏感性,同时还需要提高算法的聚类精确性。

FCM在欧氏距离和外界因素的影响下,聚类结果将会出现偏差。对于聚类算法而言,度量方式的选择对最终的聚类效果起着至关重要的作用。特征加权是一种接近个体特征最优影响程度的技术。每个特征值的大小都衡量了该特征的重要程度,本文将此特征值称为特征权重,其值在区间[0,1]中。在相应的算法中通过一个学习机制来适应权重,用较小的权重值来表示噪声特征或低质量特征,因此对于差异性的计算贡献不大。如果权重值只有0或1(即完全消除不良特征),则特征加权就减少了特征选择的过程。特征选择可以显著减少学习机制中的计算复杂程度,同时可以尽可能避免重要信息的丢失。又由于Jeffrey 散度^[10]具备较好的数值稳定性和对噪声的鲁棒性,从Jeffrey散度出发,本文提出相似性度量的概念,解释了基于Jeffrey散度的相似性度量的各种性质,提出基于Jeffrey散度的相似性度量的加权FCM聚类算法,改进后的加权FCM算法的聚类效果有更好的精确性和稳定性。

在模糊聚类中,每个聚类都被视为一个模糊集,所有的数据点都属于不同的模糊集,且有相应的隶属度。2004年,Wang等^[11]使用了FCM的全局特征加权方案,为了对特征进行加权,采用了基于学习的方法和进化适应度函数,并且采用梯度下降算法寻找合适的权值。此外,该方法基于数据分布均匀的假设,而在大多数实际数据集中并非如此。2008年,Hung等^[12]讨论了一种基于FCM的全局特征加权图像分割的算法,但是该算法计算的特征权重不适合某些极端情况,换言之,在一些数据集中,特征的权重不能恰当地表示特征的重要性^[13]。2013年,Nazari等^[14]提出自动加权和FCM集成的概念。2014年,Ferreira等^[15]对局部和全局特征加权进行了普遍的研究,利用基本的FCM和核距离,讨论了一种利用自适应距离提高聚类质量的聚类方法。2016年,Saha等^[16]设计了一种具有可分离几何距离的FCM算法,并证明了其对噪声特征扰动的鲁棒性。2018年,林甲祥等^[17]针对传统 FCM 算法无法获得令人满意的聚类结果的问题,提出了基于样本与特征双加权的自适应 FCM 聚类算法。根据Zhou等^[18]在2018的文章可知,对这种算法进行实验分析,发现大部分实验中局部自适应距离法优于全局自适应距离法,尽管这种方法可以产生比传统FCM更好的结果,但这类算法可能不适用于对大型数据集进行聚类。2020年,赵战民等^[19]针对FCM算法对噪声敏感,且不能有效分割具有类大小不均衡特性的图像的问题, 提出对类大小不敏感的模糊C均值聚类图像分割算法。

2 相关工作

2.1 FCM聚类算法

1973年, Dunn^[20]引入了FCM,随后Bezdek^[21]在1981年扩展了FCM。FCM通过最小化价值函数E_f(D,K)找到群,即

\begin{array}{l} E_{f} (K, D, O) = \\ \overset{m}{\sum_{y = 1}} \overset{c}{\sum_{x = 1}} (λ_{xy})^{f} | v_{y} - k_{x} |^{2}, 1 \leq f < \infty, (1) \end{array}

式中:f为实数,代表模糊系数。此外,成员等级对指标的影响可以通过f来控制。假设增加f,划分就会变得更模糊。研究表明,FCM在1和∞之间对f的任何值都收敛。K为样本个数,K= $U_{i = 1}^{c}$ k_i。λ_xy为样本k_x存储于D(O)_c_×_m的隶属度,在清晰划分的情况下,λ_xy=0。而当 λ_xy=1 时,O_y∈k_x为隶属矩阵元素,能量函数取决于k_x和D,D为样本k_x与聚类中心v_y的欧氏距离,即

\begin{array}{l} \overset{c}{\sum_{x = 1}} λ_{xy} = 1, y = 1,2, \dots, m, λ_{xy} \in [0,1], x = \\ 1,2, \dots, c ⋃ y = 1,2, \dots, m, (2) \\ 0 < \overset{m}{\sum_{y = 1}} λ_{xy} < c, x = 1,2, \dots, c 。 (3) \end{array}

FCM算法采取模糊迭代优化的方法,用隶属度λ_xy和样本k_x方程进行更新,即

\begin{array}{l} λ_{xy}^{i + 1} = {[\sum_{i}^{=} (\frac{v_{y} - k_{x}^{i}}{v_{y} - k_{j}^{(i)}}) \frac{2}{j^{- 1}}]}^{- 1}, (4) \\ k_{x}^{(i + 1)} = v_{y} \cdot \sum_{y}^{=} [(λ_{xy}^{i + 1})^{f}]^{- 1} \sum_{y}^{=} (λ_{xy}^{i + 1})^{f} 。 (5) \end{array}

继续更新,直到 $\{|λ_{xy}^{i + 1} - λ_{xy}^{i}|\}$ <ε,其中,ε为终止条件,ε在0~1之间,满足E_f(D,K)局部最小值^[22]。

FCM算法确定聚类中心v_y和隶属度λ_xy的一般步骤如下。

1) 用值在 $[0,1]$ 之间的随机数来初始化隶属矩阵U,使其满足(2)式;

2) 用(5)式计算聚类中心v_y,y=1,2,…,n;

3) 根据(1)式计算价值函数,如果它小于某个已知的阈值,或者它相对于上个价值函数值的改变量小于某一个阈值,那么算法停止;

4) 根据(4)式计算新的隶属矩阵U,返回步骤2。

2.2 加权的FCM算法

特征加权是在局部进行的,其方法是根据各个属性对于聚类的贡献程度不同,需要对各个属性赋予相应的权重,从而提高聚类质量。2007年,韦相等^[23]对FCM算法进行特征加权,目的是减少迭代次数,提高速度,为了便于对权值进行编码,利用规格化方法进行归一化处理,即

\begin{matrix} \{\begin{array}{l} w_{ij} = \frac{w'_{ij}}{w'_{sum}} \\ w'_{sum} = \overset{p}{\sum_{i = 1}} w'_{ij} \end{array}, 1 \leq i \leq N_{unitynum}, (6) \end{matrix}

式中:p为样本的维数;N_unitynum为遗传算法中每一代群体的个体数;w_ij为i行j列矩阵;w'_ij为对矩阵进行加权;w'_sum为对加权矩阵进行求和计算。

2.3 相似性度量方法及其性质

在聚类分析方法中,对于数据集中每个数据对象之间的关系的分析与判断,需要使用一个相似性度量方法进行测量,例如,欧氏距离、马氏距离、指数距离等经常被用到相似性度量方法中。而它们忽略了全局一致性的特征问题,因此在这一部分,给出所使用的相似性度量的定义及各种性质。

2.4 Jeffrey散度

在传统的相似性度量方法中聚类结果质量会受到加权FCM算法的影响,因此使用根据Kullback-Leibler散度改进之后的Jeffery散度来改进算法,这方种法具有数值稳定性和对噪声鲁棒性,对于方差的不稳定性的影响较小^[24]。它的定义为

\begin{array}{l} J (Y |X) = \\ \int [lo g_{2} \frac{f_{X} (x)}{m (x)} f_{X} (x) + lo g_{2} \frac{f_{Y} (x)}{m (x)} f_{Y} (x)] d x, (7) \end{array}

式中:m(x)为符合条件的概率密度函数,m(x)= $[f_{X} (x) + f_{Y} (x)]$ /2;假设随机变量Z的概率密度函数为m(x),即f_Z(x)=m(x) 。

定义1 估计Jeffrey散度J_n,它是在一组n×n的正定矩阵上定义的,即

\begin{matrix} \partial (C, D) = (C - D) lo g_{2} \frac{C}{D}, (8) \end{matrix}

式中:C= $|C|$ ;D= $|D|$ ;∂(C,D)为对矩阵C和D求偏导。

定义2 任何两个数据点c,d∈ $R_{+}^{n}$ (正实数),之间的相似性可以表示为映射S: $R_{+}^{n}$ × $R_{+}^{n}$ →R₊∪ $\{0\}$ ,可以定义为

\begin{matrix} Z (c, d) = \partial [ψ (c), ψ (d)], (9) \end{matrix}

式中:ψ(O)=diag(o₁,o₂,…,o_m),O=(o₁,o₂,…,o_m)∈ $R_{+}^{n}$ 为实正向量。

所提出的相似性度量包括如下一些属性。

命题1

\begin{matrix} Z (c, d) = Z (d, c), (10) \end{matrix}

式中:c和d为两个数据点,为Z(c,d)=∂ $[ψ (c), ψ (d)]$ 的映射。

命题2

\begin{matrix} Z (c, d) \geq 0 Z (c, d) = 0, if c = d 。 (11) \end{matrix}

定理1 相似性度量不是Bregman散度。

定理2 Z(e。c,e。d)=eZ(c,d)表示e∈ $R_{+}^{n}$ ,其中,e。c为e和c之间的Hadamard积。

定理3 相似性度量是f-散度。

3 算法改进

3.1 将Jeffery散度相似性度量与加权FCM相结合

使用Jeffery散度的相似性度量的加权FCM通过以下公式求解来实现分组。

\begin{array}{l} \min_{K = (k_{1}, k_{2}, \dots, k_{c}) \underset{D \in N}{\in} R^{n \times c}} E_{f} (K, D; O) = \\ \overset{n}{\sum_{y = 1}} \overset{c}{\sum_{x = 1}} (λ_{xy})^{f} Z (o_{y}, k_{x}), 1 \leq s < \infty, (12) \end{array}

式中:o_y为隶属矩阵的元素到样本k_x的映射,即

\begin{array}{l} N = \{D = {[λ_{xy}]}_{\begin{array}{l} x = 1,2 m, \dots, c \\ y = 1,2, \dots, n \end{array}} |λ_{xy} \in [0,1], \overset{c}{\sum_{x = 1}} λ_{xy} = \\ 1, \overset{n}{\sum_{y = 1}} λ_{xy} > 0\} 。 (13) \end{array}

(12)式精确解不存在,文献[ 25]中存在着一种交替优化方法如下所示。

定理4 假设 τ_y= $\{x |x \in [1, c], o_{y} = k_{x}^{i}\}$ ,下式是(4)式的替代式,也是证明算法的收敛性的必要条件,和(5)式是相同的。在交替优化算法中,证明E_f的收敛性。

\begin{matrix} λ_{xy}^{i + 1} = \{\begin{array}{l} \overset{c}{\sum_{i = 1}} [\frac{Z (o_{y}, k_{x}^{(i)})}{Z (o_{y}, k_{j}^{(i)})}], & τ_{y} = 0 \\ {|τ_{y}|}^{- 1}, & τ_{y} \neq 0 and x \in τ_{y} \\ 0, & τ_{y} \neq 0 and x \notin τ_{y} \end{array}, (14) \end{matrix}

式中的FCM准则可用定理5中的优化无约束FCM准则来表述。

定理5 简化FCM标准出现的公式与文献[ 25]相似,即

\begin{array}{l} \min E'_{\underset{K \in R^{n \times c}}{f}} (K; O) = \\ \overset{n}{\sum_{y = 1}} {[\overset{c}{\sum_{x = 1}} Z (o_{y}, k_{x})^{\frac{2}{1 - f}}]}^{1 - f} 。 (15) \end{array}

收敛加权FCM:假设f(γ₁,γ₂,…,γ_c)= ${(\overset{c}{\sum_{x = 1}} γ_{x}^{s})}^{\frac{1}{s}}$ ,z=(1-f)^-1<0,则(15)式表示为

\begin{array}{l} E'_{f} (k_{1}, k_{2}, \dots, k_{c}; O) = \\ \sum_{y}^{=} f (γ_{k_{1}}, γ_{k_{2}}, \dots, γ_{k_{x}}) {|_{γ_{xy}} = z (o_{y}, k_{x})}^{2} 。 (16) \end{array}

引理1 由(15)式定义,E'_f的主项为

\begin{array}{l} ma j^{l} E'_{f} = E'_{f} (k_{1}^{i}, k_{2}^{i}, \dots, k_{c}^{i}; O) + \\ \overset{c}{\sum_{y = 1}} \overset{c}{\sum_{x = 1}} \frac{d f}{d γ_{xy}} |_{(i)} [Z (o_{y,} k_{x})^{2} - Z (o_{y,} k_{x}^{i})^{2}], \\ [E'_{f} (k_{1}, k_{2}, \dots, k_{c}; O)] \leq ma j^{l} E'_{f}, (17) \end{array}

式中:导数取 $k_{1}^{i}$ , $k_{2}^{i}$ ,…, $k_{c}^{i}$ 。

定理6 (交替优化的最速下降法)如果用优化原理调整步长(17)式,则序列 $k_{x}^{i + 1}$ 以等式形式出现在交替优化算法中,(14)式和(5)式以及应用在(15)式的最速下降算法的序列是相同的。

推论1(优化加权FCM的全局收敛性)约化加权FCM算法在(12)式中说明它收敛到一个鞍点。

推论2(优化加权FCM的局部收敛性)如果K=( ${k^{*}}_{1}$ , $k_{2}^{*}$ ,…, $k_{c}^{*}$ )有Z( $k_{1}^{*}$ , $k_{2}^{*}$ ,…, $k_{c}^{*}$ )是E'_f 的局部最小,因此假设起点K⁽⁰⁾= $(k_{1}^{(0)}, k_{2}^{(0)}, \dots, k_{c}^{(0)})$ 在邻域中选取,则加权FCM算法收敛到K^*=( $k_{1}^{*}$ , $k_{2}^{*}$ ,…, $k_{c}^{*}$ )。

推论3(优化加权FCM的收敛速度)FCM在非奇异局部极小值附近与正定Hessian矩阵线性重合。

3.2 改进算法步骤

基于Jeffrey散度相似性度量的加权FCM算法的步骤如下。

1)经过对数据集进行预处理获得聚类数目k,将聚类数目k用作起始聚类中心的代表点,经过初步划分后形成簇;

2)依据预处理获得的数据集,对样本进行初始划分,得到权重向量;

3)将权重向量引入FCM算法,由(6)式对FCM算法进行特征加权,初始化隶属度矩阵u_ij,设置迭代精度参数ε,迭代次数t=0,模糊加权指数m=2;

4)根据新的聚类中心代入Jeffrey散度相似性度量中计算新的距离,重新计算隶属度和聚类中心,进行迭代循环,当聚类中心的结果不再发生变化时,算法结束。

4 实验结果与分析

4.1 实验介绍

实验环境:Windows 7操作系统,CPU i5-2410M 2.30 GHz,内存为4 GB,编程环境为MALAB R2016b。为了对改进算法进行评估和分析,使用UCI数据集和人工数据集进行实验,实验数据集如表1所示。其中UCI数据集包括Wine、Thyroid,人工数据集包括S1、Isquare2、D31、Spiral。对比算法包括:FCM、K-means、GFSFDP和JW-FCM算法。其中:K-means 算法采用欧氏距离建立相似度矩阵,是一种只适用于凸数据的聚类算法。密度峰值聚类(DPC)算法是一种能够快速搜索及查询并且利用决策图来确定聚类中心的算法^[26]。

表 1. 实验数据集属性

Table 1. Experimental data set properties

Data set	Sample number	Attributes	Number of categories
Wine	178	13	3
Thyroid	215	5	3
D31S1Isquare2Spiral	310050001741312	2222	311563

查看所有表

4.2 评价指标

本文使用聚类准确率(ACC)^[27]、调整兰德系数(ARI)^[28]以及鲁棒性(Entropy)对改进算法的聚类效果进行比较与分析。

改进算法的准确率使用ACC来进行评价,即

\begin{matrix} A_{ACC} = \frac{\overset{n}{\sum_{i = 0}} δ [_{i} map (c_{i})]}{n}, (18) \end{matrix}

式中:c_i为所提改进算法的类标签; $_{i}$ 为数据的类标签;δ(x,y)为函数;map(x)为映射函数对所获取的中心和真实的中心进行映射。

调整ARI为

\begin{matrix} A_{ARI} = \frac{2 (ad - bc)}{(a + b) (b + d) + (a + c) (c + d)}, (19) \end{matrix}

式中:a为归属于隶属矩阵U的同类且属于V的同类的数据的对数目;b为归属于U的同类但属于V的不同类的数据的对数目;c为归属于U的不同类而归属于V的同类的数据的对数目;d为归属于U的不同类且归属于V的不同类的数据的对数目。ARI越近似 1 说明聚类效果越好,越临近 0 说明聚类效果越差。

Entropy即熵值,在1854年由Clausius^[29]提出,表示一个系统的内在混乱程度。Entropy的取值在[0,1]间,取值越小表示算法中的混乱程度越低,聚类效果越好。

4.3 实验与分析

在本节中进行了多组实验,并将本文所提基于Jeffery散度的相似性度量加权FCM聚类算法与相关算法(FCM、K-means和DPC算法)进行了对比与分析。所用到的数据集主要包括:D31、Isquare2、S1、Spiral 4个人工数据集以及Wine和Thyroid 2个UCI数据集。其中D31、Isquare2、S1、Spiral均为二维数据集,D31的数据样本数量较多,Wine和Thyroid均为多维数据集。

本组实验分别在D31、Isquare2、S1 、Spiral 4个人工数据集以及Wine和Thyroid 2个UCI数据集上进行,实验数据集属性如表1所示,实验收敛性结果如图1所示。从图1可以看出每个算法的收敛效率的情况,K-means和DPC收敛性较弱,FCM较好,JW-FCM收敛性相对其他几个算法收敛性最好。聚类效果图如图2~4所示。从图2可以看出,FCM、K-means 和 DPC 算法在Spiral数据集上的聚类效果没有正确地划分类别,而JW-FCM算法能将数据正确地划分类别。在图3中FCM、K-means 和 DPC 算法在S1数据集上的聚类效果依然没有正确地聚类,而JW-FCM算法同样能将此数据正确地划分类别。在图4中,对于ISquare2数据集,JW-FCM算法聚类效果是比较好的,FCM 算法仅次之,而K-means 、DPC算法的聚类效果是比较差的。

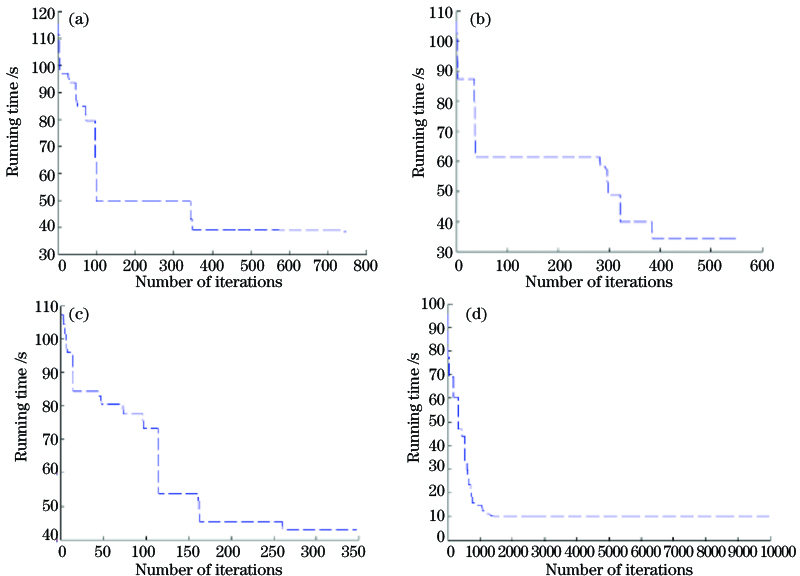
图 1. 四种聚类算法的收敛性分析。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 1. Convergence analysis of four clustering algorithms. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

下载图片查看所有图片

图 2. 四种聚类算法对数据集Spiral聚类结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 2. Clustering results of four clustering algorithms on Spiral data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

下载图片查看所有图片

图 3. 四种聚类算法对数据集S1聚类的结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 3. Clustering results of four clustering algorithms on S1 data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

下载图片查看所有图片

图 4. 四种聚类算法对数据集ISquare2聚类的结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 4. Clustering results of four clustering algorithms on ISquare2 data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

下载图片查看所有图片

通过对图2~4三组实验的可视化对比实验分析可知:JW-FCM算法比K-means、FCM和 DPC 算法更擅长对复杂形状的数据进行聚类。以上四种聚类算法在人工数据集上的性能对比如表2所示,从表2可以看出,JW-FCM算法在Spiral、S1、ISquare2数据集上的聚类指标值都是1,在wine数据集的聚类指标值JW-FCM算法均大于其他算法,聚类效果最好。根据表中聚类指标值来看,JW-FCM算法聚类性能最优,FCM次之,而K-means和DPC相对来说效果一般。加入不同比例的噪声数据后,FCM和K-means的Entropy变化较大,DPC和JW-FCM算法的Entropy指标变化较为接近。综上,JW-FCM算法在保持较高的准确性的同时,还具有较好的鲁棒性。由此可见,用Jeffrey散度相似性度量代替欧氏距离很大程度上提高了加权FCM算法的聚类性能,与此同时,提高了聚类效果的稳定性和准确性,此外为了更直观地展示对比效果,将各个数据进行求均值,如表2最后一行Mean所示,ACC对比图如图5所示,ARI对比图如图6所示。

表 2. 四种聚类算法在数据集上的性能对比

Table 2. Performance comparison of four clustering algorithms on data set

Data set	ACC							ARI								Entropy
Data set	FCM	K-means		DPC		JW-FCM		FCM		K-means		DPC		JW-FCM		FCM		K-means		DPC		JW-FCM
Wine	0.408		0.456		0.441		0.898		0.007		0.006		0.012		0.854		0.150		0.250		0.160		0.100
Thyroid	0.615		0.653		0.524		0.750		0.168		0.196		0.075		0.698		0.600		0.780		0.470		0.420
D31	0.875		0.358		0.846		0.993		0.654		0.324		0.756		0.882		0.320		0.320		0.230		0.180
S1	0.657		0.685		0.876		1.000		0.598		0.698		0.897		1.000		0.760		0.890		0.760		0.630
Isquare2	0.976		0.764		0.985		1.000		0.975		0.708		0.968		1.000		0.080		0.270		0.130		0.060
Spiral	0.356		0.405		0.529		1.000		0.003		0.011		0.276		1.000		0.960		0.960		0.660		0.460
Mean	0.648		0.554		0.700		0.940		0.401		0.324		0.497		0.906		0.478		0.578		0.402		0.308

查看所有表

图 5. ACC指标对比图

Fig. 5. Comparison of ACC indicators

下载图片查看所有图片

图 6. ARI指标对比图

Fig. 6. Comparison of ARI indicators

下载图片查看所有图片

比较了收敛性、准确率、聚类效果之后,在实验中,将噪声数据按照0.1、0.2、0.3、0.4、0.5的比例加入6个数据集中分别聚类,实验结果如图7~12所示,可以看出,在D31、Isquare2、S1、Spiral 、Wine和Thyroid六个数据集下,JW-FCM的Entropy值最低,混乱程度越低,聚类效果最好,证明了本文算法具有较好的噪声鲁棒性。

图 7. 在数据集Wine上的鲁棒性对比

Fig. 7. Robustness comparison on Wine data set

下载图片查看所有图片

图 8. 在数据集Thyroid上的鲁棒性对比

Fig. 8. Robustness comparison on Thyroid data set

下载图片查看所有图片

图 9. 在数据集D31上的鲁棒性对比

Fig. 9. Robustness comparison on D31 data set

下载图片查看所有图片

图 10. 在数据集S1上的鲁棒性对比

Fig. 10. Robustness comparison on S1 data set

下载图片查看所有图片

图 11. 在数据集Isquare2上的鲁棒性对比

Fig. 11. Robustness comparison on Isquare2 data set

下载图片查看所有图片

图 12. 在数据集Spiral上的鲁棒性对比

Fig. 12. Robustness comparison on Spiral data set

下载图片查看所有图片

5 结论

传统的FCM算法在使用欧氏距离相似性度量中,只考虑数据点之间的局部一致性问题,所以聚类效果差,对此本文将FCM算法进行特征加权,引入遗传算法加快算法的收敛速度,再结合Jeffrey散度对算法进行改进,在加权FCM算法中使用Jeffrey相似性度量代替了欧氏距离,所提JW-FCM算法保证了局部极小。通过将FCM、K-means、DPC算法和本文JW-FCM算法在UCI数据集及人工数据集中进行实验比较及分析,验证了改进算法具有较好的聚类效果,较原始算法有所提升,并且具备高效性、鲁棒性及准确性。但是该算法在处理大规模数据时,其时间复杂度相对较高,同时复杂性度量的研究也是算法下一步的主要研究目标。

参考文献

[1] 张静, 付建鹏, 李新慧. 基于低秩正则化异构张量分解的子空间聚类算法[J]. 激光与光电子学进展, 2018, 55(7): 071003.

Zhang J, Fu J P, Li X H. Low-rank regularized heterogeneous tensor decomposition algorithm for subspace clustering[J]. Laser & Optoelectronics Progress, 2018, 55(7): 071003.

[2] Pei X B, Wu T, Chen C B. Automated graph regularized projective nonnegative matrix factorization for document clustering[J]. IEEE Transactions on Cybernetics, 2014, 44(10): 1821-1831.

[3] 童绪军, 吴义春. 数据挖掘中一种改进的谱组合聚类算法[J]. 太赫兹科学与电子信息学报, 2020, 18(3): 497-503.

Tong X J, Wu Y C. An improved spectral ensemble clustering algorithm in data mining[J]. Journal of Terahertz Science and Electronic Information Technology, 2020, 18(3): 497-503.

[4] 王千, 王成, 冯振元, 等. K-means聚类算法研究综述[J]. 电子设计工程, 2012, 20(7): 21-24.

Wang Q, Wang C, Feng Z Y, et al. Review of K-means clustering algorithm[J]. Electronic Design Engineering, 2012, 20(7): 21-24.

[5] Hathaway R J, Bezdek J C, Hu Y K. Generalized fuzzy c-means clustering strategies using Lp norm distances[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(5): 576-582.

[6] 周水庚, 周傲英, 曹晶. 基于数据分区的DBSCAN算法[J]. 计算机研究与发展, 2000, 37(10): 1153-1159.

Zhou S G, Zhou A Y, Cao J. A data-partitioning-based DBSCAN algorithm[J]. Journal of Computer Research and Development, 2000, 37(10): 1153-1159.

[7] Chakraborty S, Das S. K-means clustering with a new divergence-based distance metric: convergence and performance analysis[J]. Pattern Recognition Letters, 2017, 100: 67-73.

[8] BanerjeeA, MeruguS, DhillonI, et al. Clustering with bregman divergences[C] //Proceedings of the 2004 SIAM International Conference on Data Mining, Philadelphia, PA: Society for Industrial and Applied Mathematics, 2004.

[9] 朱占龙, 王军芬. 基于自适应模糊C均值与后处理的图像分割算法[J]. 激光与光电子学进展, 2018, 55(1): 011004.

Zhu Z L, Wang J F. Image segmentation based on adaptive fuzzy C-means and post processing correction[J]. Laser & Optoelectronics Progress, 2018, 55(1): 011004.

[10] PuzichaJ, HofmannT, Buhmann JM. Non-parametric similarity measures for unsupervised texture segmentation and image retrieval[C] //Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, June 17-19, 1997, San Juan, Puerto Rico, USA. New York: IEEE Press, 1997: 267- 272.

[11] Wang X Z, Wang Y D, Wang L J. Improving fuzzy c-means clustering based on feature-weight learning[J]. Pattern Recognition Letters, 2004, 25(10): 1123-1132.

[12] Hung W L, Yang M S, Chen D H. Bootstrapping approach to feature-weight selection in fuzzy c-means algorithms with an application in color image segmentation[J]. Pattern Recognition Letters, 2008, 29(9): 1317-1325.

[13] Xing HJ, Wang XZ, Ha MH. A comparative experimental study of feature-weight learning approaches[C] //2011 IEEE International Conference on Systems, Man, and Cybernetics, October 9-12, 2011, Anchorage, AK, USA. New York: IEEE Press, 2011: 3500- 3505.

[14] NazariM, ShanbehzadehJ, SarrafzadehA. Fuzzy c-means based on automated variable feature weighting[C] //Proceedings of the International MultiConference of Engineers and Computer Scientists, IMECS 2013, March 13 - 15, 2013, Hong Kong.

[15] Ferreira M R P, de Carvalho F D A T. Kernel fuzzy c-means with automatic variable weighting[J]. Fuzzy Sets and Systems, 2014, 237: 1-46.

[16] Saha A, Das S. Geometric divergence based fuzzy clustering with strong resilience to noise features[J]. Pattern Recognition Letters, 2016, 79: 60-67.

[17] 林甲祥, 吴丽萍, 巫建伟, 等. 基于样本与特征双加权的自适应FCM聚类算法[J]. 黑龙江大学自然科学学报, 2018, 35(2): 244-252.

Lin J X, Wu L P, Wu J W, et al. Adaptive FCM clustering algorithm based on sample and feature weights[J]. Journal of Natural Science of Heilongjiang University, 2018, 35(2): 244-252.

[18] Zhou Z P, Zhu S W. Kernel-based multiobjective clustering algorithm with automatic attribute weighting[J]. Soft Computing, 2018, 22(11): 3685-3709.

[19] 赵战民, 朱占龙, 刘永军, 等. 对类大小不敏感的图像分割模糊C均值聚类方法[J]. 激光与光电子学进展, 2020, 57(2): 021001.

Zhao Z M, Zhu Z L, Liu Y J, et al. Fuzzy C-means clustering algorithm for image segmentation insensitive to cluster size[J]. Laser & Optoelectronics Progress, 2020, 57(2): 021001.

[20] Dunn J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1973, 3(3): 32-57.

[21] Bezdek JC. Pattern recognition with fuzzy objective function algorithms[M]. Boston: Springer, 1983, 442: 1- 13.

[22] Seal A, Karlekar A, Krejcar O, et al. Fuzzy c-means clustering using Jeffreys-divergence based similarity measure[J]. Applied Soft Computing, 2020, 88: 106016.

[23] 韦相, 汤兴华. 一种改进了的基于遗传算法的维特征加权改进FCM算法[J]. 红河学院学报, 2007, 5(2): 39-42.

Wei X, Tang X H. Advanced dimension power FCM arithmetic with genetics[J]. Journal of Honghe University, 2007, 5(2): 39-42.

[24] 郑瑾, 尤红建. 基于Radon变换和Jeffrey散度的SAR图像变化检测方法[J]. 雷达学报, 2012, 1(2): 182-189.

Zheng J, You H J. Change detection with SAR images based on radon transform and Jeffrey divergence[J]. Journal of Radars, 2012, 1(2): 182-189.

[25] Groll L, Jakel J. A new convergence proof of fuzzy c-means[J]. IEEE Transactions on Fuzzy Systems, 2005, 13(5): 717-720.

[26] 陈叶旺, 申莲莲, 钟才明, 等. 密度峰值聚类算法综述[J]. 计算机研究与发展, 2020, 57(2): 378-394.

Chen Y W, Shen L L, Zhong C M, et al. Survey on density peak clustering algorithm[J]. Journal of Computer Research and Development, 2020, 57(2): 378-394.

[27] Shang F H, Jiao L C, Shi J R, et al. Fast affinity propagation clustering: a multilevel approach[J]. Pattern Recognition, 2012, 45(1): 474-486.

[28] Vinh NX, EppsJ, BaileyJ. Bibliometrics: information theoretic measures for clusterings comparison[C] //The International Conference on Machine Learning, July 11-14, 2010, Qingdao, China. New York: ACM, 2010: 2837- 2854.

[29] Clausius R. Ueber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie[J]. Annalen Der Physik Und Chemie, 1854, 169(12): 481-506.

3.1 将Jeffery散度相似性度量与加权FCM相结合

吴辰文, 马宁, 蒋雨璠. 基于Jeffrey散度相似性度量的加权FCM聚类算法[J]. 激光与光电子学进展, 2021, 58(8): 0810006. Chenwen Wu, Ning Ma, Yufan Jiang. Weighted FCM Clustering Algorithm Based on Jeffrey Divergence Similarity Measure[J]. Laser & Optoelectronics Progress, 2021, 58(8): 0810006.

基于Jeffrey散度相似性度量的加权FCM聚类算法 下载： 828次

1 引言

2 相关工作

2.1 FCM聚类算法

2.2 加权的FCM算法

2.3 相似性度量方法及其性质

2.4 Jeffrey散度

3 算法改进

3.1 将Jeffery散度相似性度量与加权FCM相结合

3.2 改进算法步骤

4 实验结果与分析

4.1 实验介绍

表 1. 实验数据集属性

Table 1. Experimental data set properties

4.2 评价指标

4.3 实验与分析

图 1. 四种聚类算法的收敛性分析。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 1. Convergence analysis of four clustering algorithms. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

图 2. 四种聚类算法对数据集Spiral聚类结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 2. Clustering results of four clustering algorithms on Spiral data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

图 3. 四种聚类算法对数据集S1聚类的结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 3. Clustering results of four clustering algorithms on S1 data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

图 4. 四种聚类算法对数据集ISquare2聚类的结果。(a) FCM;(b) K-means;(c) DPC;(d) JW-FCM

Fig. 4. Clustering results of four clustering algorithms on ISquare2 data set. (a) FCM; (b) K-means; (c) DPC; (d) JW-FCM

表 2. 四种聚类算法在数据集上的性能对比

Table 2. Performance comparison of four clustering algorithms on data set

图 5. ACC指标对比图

Fig. 5. Comparison of ACC indicators

图 6. ARI指标对比图

Fig. 6. Comparison of ARI indicators

图 7. 在数据集Wine上的鲁棒性对比

Fig. 7. Robustness comparison on Wine data set

图 8. 在数据集Thyroid上的鲁棒性对比

Fig. 8. Robustness comparison on Thyroid data set

图 9. 在数据集D31上的鲁棒性对比

Fig. 9. Robustness comparison on D31 data set

图 10. 在数据集S1上的鲁棒性对比

Fig. 10. Robustness comparison on S1 data set

图 11. 在数据集Isquare2上的鲁棒性对比

Fig. 11. Robustness comparison on Isquare2 data set

图 12. 在数据集Spiral上的鲁棒性对比

Fig. 12. Robustness comparison on Spiral data set

5 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

基于Jeffrey散度相似性度量的加权FCM聚类算法下载： 828次