激光与光电子学进展, 2019, 56 (1): 011503, 网络出版: 2019-08-01
基于正交迭代的参考点不确定相机位姿估计  下载: 1373次
下载: 1373次
Camera Pose Estimation with Uncertain Reference Point Based on Orthogonal Iterative
机器视觉 单目视觉 相机位姿估计 正交迭代 不确定参考点 最大似然估计 machine vision monocular vision camera pose estimation orthogonal iterations uncertain reference point maximum likelihood estimation
摘要
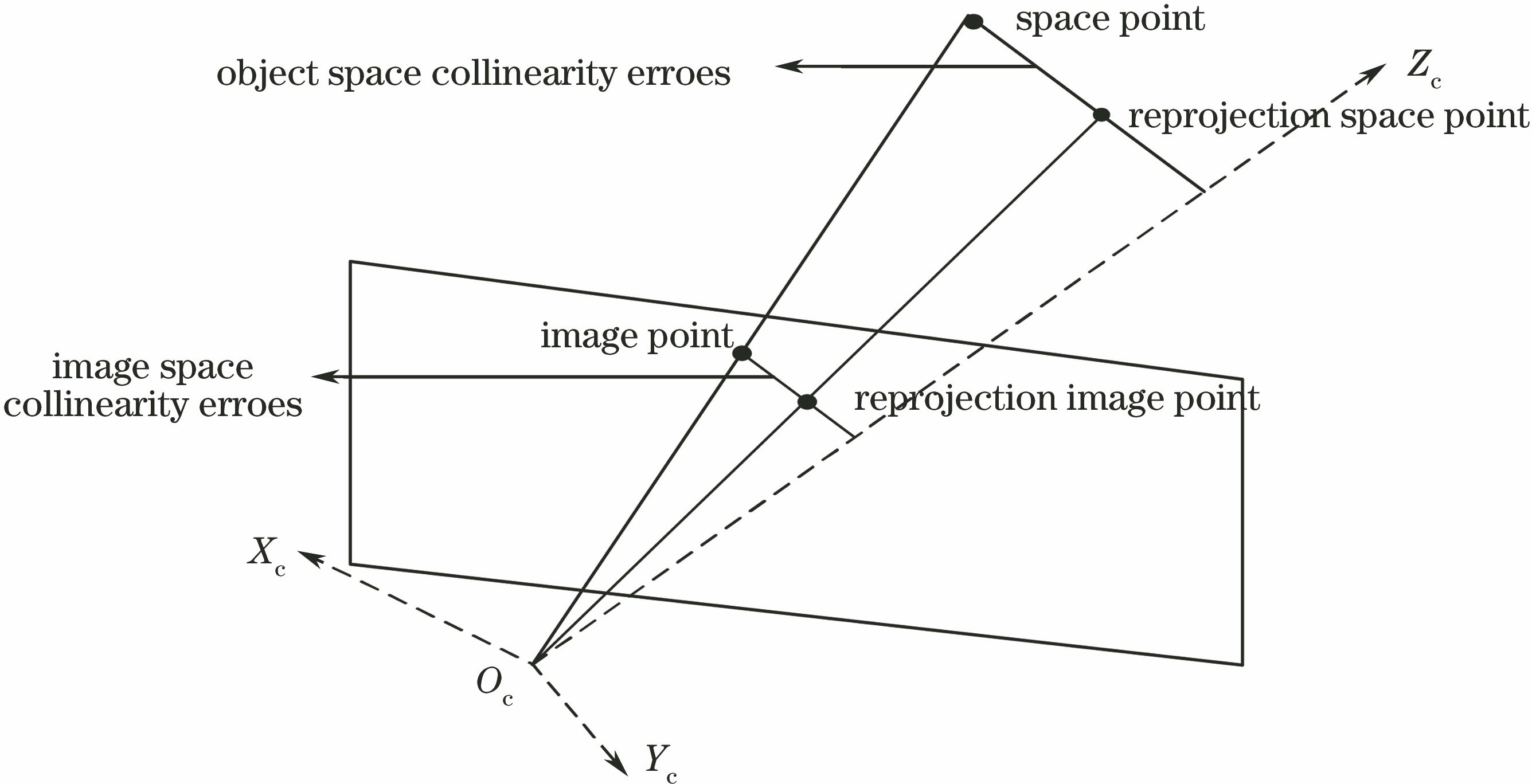
相机的位姿估计广泛应用于计算机视觉和机器人学等领域。针对相机位姿估计的稳定性与实时性,基于正交迭代算法,提出了一种考虑空间参考点不确定性的相机位姿估计算法。该算法的关键思想是在考虑摄像头畸变的情况下,根据参考点的位置特征获得相应权值,并利用加速正交迭代思想对迭代过程中的重复计算进行规整,最小化加权重投影物方残差函数获得相机位姿。模拟数据实验和真实图像实验表明,该算法计算精度更高,速度更快,时间复杂度较低。在空间参考点深度较大或者偏离摄像头光轴的情况下,该算法的时间复杂度和精度均优于现有的正交迭代算法,从而实现了相机位姿估计的实时性。
Abstract
Camera pose estimation is widely used in computer vision and robotics. Aiming at the stability and real-time performance of camera pose estimation, a camera pose estimation algorithm considering the uncertainty of spatial reference points based on orthogonal iterative algorithm is proposed. The key idea of the algorithm is to obtain the weights of the corresponding feature points in consideration of camera distortion and use an accelerated orthogonal iterative algorithm to regularize the repeated calculations in the iterative process. And the camera pose is obtained by minimizing the weighted re-projection object residual function. Results of simulation data experiments and real image experiment show that the proposed algorithm has higher calculation accuracy, faster speed, and lower time complexity. In the case of deep spatial feature points or the feature points deviating from the optical axis of the camera, the time complexity and accuracy of the algorithm are better than the existing orthogonal iterative algorithms, indicating its feasibility in the real-time estimation of camera pose.
李丽媛, 李文韬, 许海燕, 张卓, 谢迎娟, 张学武. 基于正交迭代的参考点不确定相机位姿估计[J]. 激光与光电子学进展, 2019, 56(1): 011503. Liyuan Li, Wentao Li, Haiyan Xu, Zhuo Zhang, Yingjuan Xie, Xuewu Zhang. Camera Pose Estimation with Uncertain Reference Point Based on Orthogonal Iterative[J]. Laser & Optoelectronics Progress, 2019, 56(1): 011503.