Observation of Zeeman splitting effect in a laser-driven coil
1 I. INTRODUCTION
The Zeeman effect was one of the most significant spectroscopic discoveries of the nineteenth century. It has been applied in various research fields since it was observed in 1896.1 In atomic and molecular physics, the Zeeman effect plays a key role in calculating hyperfine atomic structures.2 In materials science, for example, the observed Zeeman splitting and oscillator strengths reveal the symmetry and fine crystal structure of Cr-doped GaAs.3 In fusion research, the Zeeman effect is used not only to measure the magnetic field (B-field) strength, but also to study impurities in particle transport in magnetically confined fusion plasmas through determination of line positions, shapes, and hence species temperatures.4,5 In astrophysics, the Zeeman effect makes it possible to infer the B-field strength in various remote objects from telescope observations.6–9 This is of great help in understanding the evolution of these objects and related astrophysical phenomena, such as jets10 and magnetic reconnection.11,12 In laser–plasma research, the Zeeman effect is a powerful tool for measuring the intensity of strong B-fields at local plasma positions.13,14 It is very helpful in studies of strongly magnetized plasmas, in the context, for example, of magnetized fast ignition15 and magnetohydrodynamic effects.16
In recent years, laser-driven coils have shown promise for laboratory generation of B-fields.17–25 This method of B-field generation has attracted interest in many areas of research owing to the high field amplitudes that it can achieve and its controllable characteristics. A variety of techniques have been used to measure a rapidly rising B-field with small spatial and short temporal scales. One traditional method is to use a differential magnetic probe, also known as a B-dot probe.17,19,20 This probe provides information on both the amplitude and temporal evolution of a B-field. However, it is vulnerable to the electromagnetic noise generated by laser–plasma interactions and cannot measure local B-fields directly. It can only be deployed several centimeters away from the coil center, and consequently the values of smaller B-fields (of the order of 102–103 T) at the coil center have to be extrapolated from measured B-fields of only 10−4–10−1 T. Another new approach to the measurement of laser-generated B-fields is through Faraday rotation,18,20,24 which can also provide both the amplitude and temporal evolution of the B-fields. However, this technique usually requires an external synchronized polarized light probe and a magneto-optical crystal positioned several millimeters away from the coil center. The main limitation of this diagnostic is the opacity of magneto-optical crystals and the consequent blacking out of light signals.18 Another diagnostic for laser-driven B-fields is provided by proton radiography.20–22,26 This measurement method can infer the local B-field distribution, but an additional relativistic laser is needed to generate high-energy protons. The temporal range is usually about 100 ps.
In this study, the Zeeman effect is applied for the first time to measure the B-field generated by a laser-driven coil. The copper plasma expanding from the coil surface to the coil center is used as an emission source. We choose the Cu I 3d104p2P03/2 → 3d94s22D5/2, 3d104d2D3/2 → 3d104p2P01/2, and 3d104d2D5/2 → 3d104p2P03/2 spectral lines emitted from the hot plasma. Their wavelengths are 510.5541, 515.3235, and 521.8202 nm, respectively.
2 II. EXPERIMENTS
The experiments were performed at the Shengguang-II laser facility. An Ω-shaped copper coil was employed, with the configuration is shown in Fig. 1(b). The inner diameter of the coil was 0.8 mm, and its opening width was 0.5 mm. The coil wire had a cross section of 200 × 200 µm2. The diameter of the disk end was ∼1 mm. The coil axis was parallel to the z axis. The experimental setup is illustrated in Fig. 1(a). Eight laser beams with a total energy of ∼2 kJ were divided into two bunches and focused onto two sides of the bottom disk of the Ω-shaped coil target at a wavelength of 351 nm and duration of 1 ns. The focal spot was about 150 µm in full width at half maximum (FWHM). The laser intensity was ∼5.6 × 1015 W/cm2. A strong magnetic field was generated at the coil center due to the cold-electron return current from the focal spot to the top end of the coil. The mechanism is the same as that in our previous studies.19,24–26
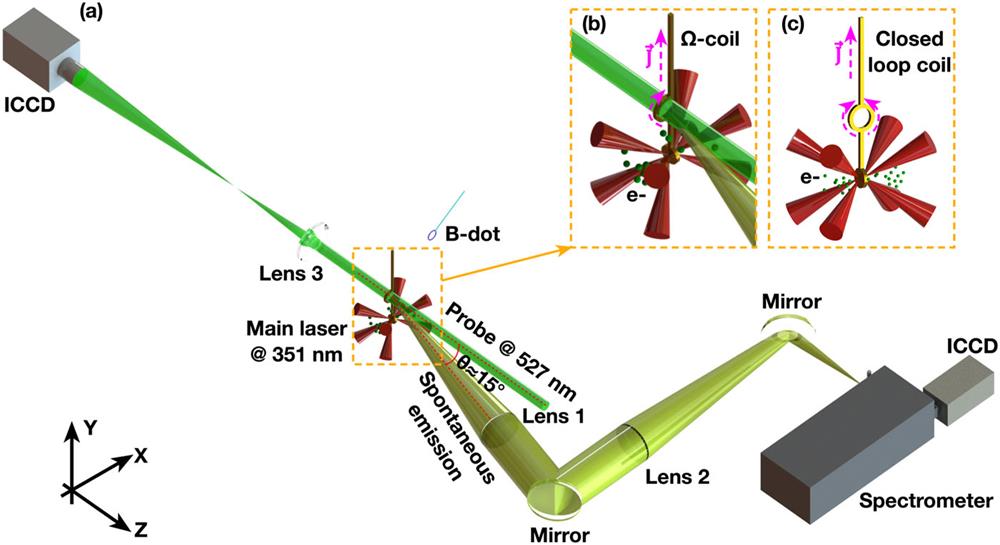
Fig. 1. (a) Experimental setup. (b) Configuration of Ω-shaped coil. (c) Configuration of closed-loop coil.
The coil surface was ionized as a result of simultaneous Joule heating and x-ray radiation from the laser focal spot. The surface plasma expanded toward the coil center. Shadowgraphy with a magnification of ∼4 was used to detect the plasma evolution inside the coil along the −z direction with a synchronized 70 ps probe laser at a wavelength of 527 nm. The Zeeman effect was used to detect the laser-driven B-field strength. The central hot plasma was used as an emission source, and this was imaged onto a spectrometer entrance slit 20 µm wide with a total magnification of ∼1.7. The image was transformed into spectral signals on an intensified charged coupled device (ICCD) after diffraction by a grating with 150 grooves/mm. The spectral resolution was ∼0.39 nm. The axis of the first collection lens was at ∼15° to the axis of the Ω-shaped coil. In addition, a differential B-dot probe was also used to measure the B-field strength for comparison. It was placed ∼3 cm away from the coil center, with the pickup coil plane in the x–y plane at z = 0.
3 III. RESULTS AND DISCUSSION
3.1 A. Magnetic fields measured with B-dot probe
Figure 2 shows the temporal evolution of the average Bz (the z component of the B-field strength) at the B-dot probe position at a laser intensity of ∼5.6 × 1015 W/cm2. The peak magnetic field measured at the local B-dot position, BB-dot, was 0.020 ± 0.002 T. The spatial distribution of the magnetic field was calculated using the three-dimensional magnetostatic code RADIA.27 The whole target geometry, including the open coil and the straight wires, was modeled precisely to allow accurate extrapolation of the magnetic field distribution. The current in the coil was adjusted to match the calculated field strength with the measured value at the position of the B-dot probe. The peak current in the coil target was estimated to be ∼38 kA. Figure 3(a) shows the calculated two-dimensional magnetic field distribution in the x–y plane at z = 0 with the peak current. The B-field strength at the coil center, Bcenter, was estimated to be 22.9 ± 0.1 T.

Fig. 2. Temporal evolution of the measured B-field strength at the position of the B-dot probe. The vertical error bars correspond to the standard deviation of two shots.

Fig. 3. Calculated two-dimensional magnetic field distribution in the x –y plane at z = 0: (a) Ω-shaped coil; (b) closed-loop coil.
3.2 B. Zeeman measurements
Figure 4 shows temporally resolved shadowgraphs before and after a laser shot. Compared with the shadowgraph before the laser shot in Fig. 4(a), Fig. 4(b) at a delay time of 3.5 ns shows an obvious increase in wire width. This demonstrates that the coil surface is ionized. This is probably due to Ohmic heating and x-ray radiation. The ionized plasma has expanded from the coil’s inner surface toward its center. Figure 4(c) at 6.0 ns reveals a higher plasma concentration that has formed a high-density area at the coil center. This central plasma with a width of ∼395 µm along the y axis was employed as an emission source in our experiments using the Zeeman effect to detect the local B-field strength at the coil center.

Fig. 4. Shadowgraphs in the x –y plane: (a) before laser shot; (b) at a delay time t = 3.5 ns; (c) at a delay time t = 6.0 ns. The dark regions demonstrate that the plasma density is so high that the probe light cannot penetrate it.
In our Zeeman measurements, three Cu I transitions were selected: (1) 3d104p2P03/2 → 3d94s22D5/2, (2) 3d104d2D3/2 → 3d104p2P01/2, and (3) 3d104d2D5/2 → 3d104p2P03/2. According to the theory of the Zeeman effect,1,28 two σ components should be detected, because the observation angle is nearly parallel to the magnetic field. By comparing the time-integrated spectrum of the Ω-shaped coil and that obtained from the NIST Atomic Spectra Database29 shown in Fig. 5(a), the Cu I lines at these three transitions exhibit an obvious splitting. The experimental π component was deduced from the center of neighboring pairs of σ peaks. The respective wavelengths were 510.42, 515.16, and 521.47 nm. The splitting distance ΔλB between the σ and π lines was 0.39 nm for all three transitions. In addition, compared with the NIST spectrum,29 the π line shifted owing to Doppler effects. These results demonstrate that the central plasma propagated in the z direction. The velocity was estimated to be ∼129.6 ± 39.8 km/s.
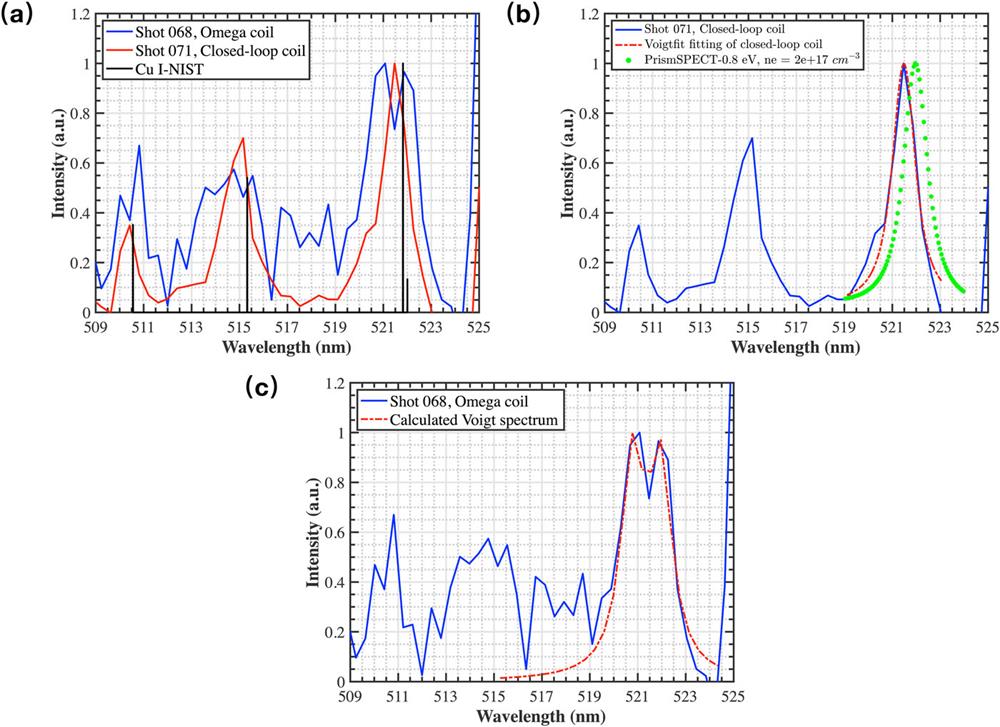
Fig. 5. (a) Comparison between the observed spectra from the Ω-shaped and closed-loop coils and the Cu I spectrum obtained from the NIST Atomic Spectra Database at T e = 0.8 eV. (b) Comparison between the observed spectrum from the closed-loop coil and calculated spectra: the red dashed curve is the Voigt fitting for the closed-loop coil spectrum at 521.47 nm, and the green dotted curve is one typical PrismSPECT Cu I line shape convolved with instrumental broadening computed at T e = 0.8 eV and n e = 2 × 1017 cm−3. (c) Comparison between the observed spectrum from the Ω-shaped coil and the calculated Voigt spectrum.
To verify the role of B-fields, a closed copper loop target was also used in our experiments. The structure of this coil is shown in Fig. 1(c). The inner diameter and cross section of the coil, as well as the experimental setup, were the same as those used for the Ω-shaped coil. The only difference was that the coil was a closed loop, rather than an open configuration. Compared with the Ω-shaped coil, the return current flowed symmetrically along the closed loop. Therefore, the B-field strength at the coil center was, in theory, zero, as shown in Fig. 3(b). The red line in Fig. 5(a) represents the spontaneous emission spectrum of the closed-loop coil. It is obvious that the closed-loop coil did not cause a splitting effect. Therefore, the splitting can be attributed to a B-field effect.
To evaluate the magnetic field strength for linear Zeeman effects, anomalous Zeeman effects and Paschen–Back effects30 should first be distinguished when the spin angular momentum S is nonzero. The fine-structure split distance ΔλLS between transition (3) and the transition 3d104d2D3/2 → 3d104p2P03/2 due to spin–orbit coupling is 0.1868 nm. Because ΔλLS < ΔλB = 0.39 nm, this demonstrates that the magnetic field strength was strong enough to disrupt the spin–orbit coupling, leading to spin angular momentum S and orbital angular momentum L coupling more strongly to the external magnetic field than to each other, i.e., the Paschen–Back effect. Thus, the Paschen–Back effect was dominant in our experiments. The energy shift ΔE in an external magnetic field is
Table 1. Summary of spectra.
|
One advantage of measuring the Zeeman effect compared with other B-field measurements is that the electron temperature Te and density ne can be derived from the line shapes and relative intensities of some atomic lines. In our experiments, the line intensity ratio between transitions (1) and (3), I1/I3, was used to calculate the plasma temperature Te. According to the Boltzmann equation, under the assumption of local thermodynamic equilibrium (LTE),
The spectral width at transition (3) of the closed-loop target was used to derive the electron density ne. The spectral shape of the Cu I multiplet was mainly affected by Stark broadening, Doppler broadening, and instrumental broadening. Because Stark broadening has a Lorentz profile, while Doppler and instrumental broadening have Gaussian profiles, the whole spectral profile should be a convolution of Gaussian (G) and Lorentzian (L) profiles. Therefore, to obtain accurate FWHM values, the Voigt function was applied to fit the experimental spectra shape. The Voigt function is expressed as
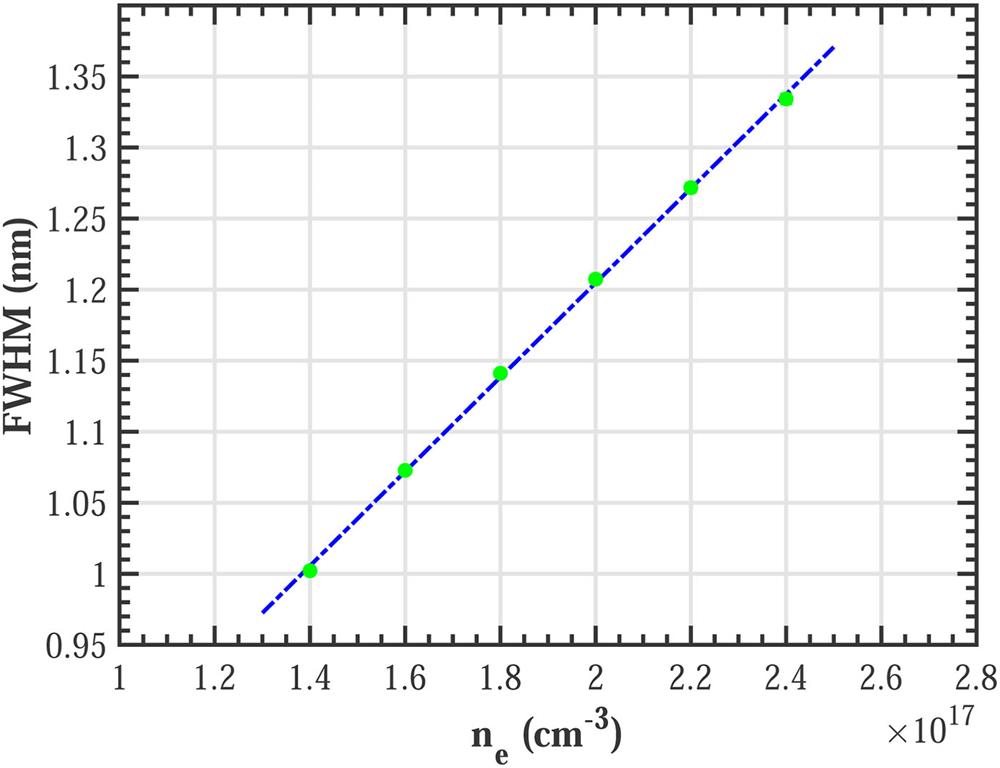
Fig. 6. FWHM of line at transition (3) as a function of electron density n e computed with PrismSPECT at T e = 0.8 eV.
4 IV. CONCLUSIONS
For what we believe to be the first time, the Zeeman effect has been applied to measure the local magnetic field generated by a laser-driven coil. The results show good agreement with B-dot probe measurements. Compared with other common magnetic field diagnostics, much more local plasma information, including plasma temperature and density, can be derived from the Zeeman spectra. In addition, when the magnetic field is strong enough to split ultraviolet or x-ray light, the Zeeman effect will be a very powerful diagnostic tool to detect the magnetic field inside a high-density plasma. Moreover, the rapid development of laser-driven magnetic fields also offers a new opportunity to study nonlinear Zeeman effects in the laboratory. This will open a new approach for studying astrophysical phenomena33,34 and fundamental physics in the future.
5 ACKNOWLEDGMENTS
Acknowledgment. This work was supported in part by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant Nos. XDA25010100, XDA25010300, and XDA25030100), the National Natural Science Foundation of China (Grant Nos. U1930107 and 11827807), and the Japanese Ministry of Education, Science, Sports, and Culture through Grants-in-Aid, KAKENHI (Grant No. 21H04454).
[1] P.Zeeman. XXXII. On the influence of magnetism on the nature of the light emitted by a sub-stance. London, Edinburgh Dublin Philos. Mag. J. Sci., 1897, 43(262): 226-239.
[2] W. L.Virgo. Simultaneous Stark and Zeeman effects in atoms with hyperfine structure. Am. J. Phys., 2013, 81: 936-942.
[3] L.Eaves, C.Uihlein. High-magnetic-field Zeeman spectroscopy of the 0.84-eV Cr-related emission and absorption line in GaAs(Cr): Experiment and theory. Phys. Rev. B, 1982, 26: 4473-4484.
[4] K.Fujii, M.Goto, M.Hasuo, A.Iwamae, K.Mizushiri, S.Morita, T.Shikama. A simultaneous measurement of polarization-resolved spectra of neutral helium 23P–33D, 21P–31D and 23P–33S emissions from the periphery of a Large Helical Device plasma. Plasma Phys. Controlled Fusion, 2011, 53: 105012-105024.
[5] S.Brezinsek, C. C.Chu, J. D.Hey, P.Mertens, B.Unterberg. Oxygen ion impurity in the TEXTOR tokamak boundary plasma observed and analysed by Zeeman spectroscopy. J. Phys. B: At., Mol. Opt. Phys., 2002, 35: 1525-1553.
[6] R. J.Boyle, D.Deming, D. E.Jennings, G.Wiedemann. Solar magnetic field studies using the 12 micron emission lines. I. Quiet-sun time series and sunspot slices: Erratum. Astrophys. J., 1989, 338: 1193.
[7] H. W.Babcock. Zeeman effect in stellar spectra. Astrophys. J., 1947, 105: 105.
[8] R. I.Anderson, A.Reiners, S. K.Solanki. On detectability of Zeeman broadening in optical spectra of F- and G-dwarfs. Astron. Astrophys., 2010, 522: A81.
[9] J. D.Bailey. Measuring the surface magnetic fields of magnetic stars with unresolved Zeeman splitting. Astron. Astrophys., 2014, 568: A38.
[10] J.Ferreira. Magnetically-driven jets from Keplerian accretion discs. Astron. Astrophys., 1997, 319: 340-359.
[11] R. A.Kopp, G. W.Pneuman. Magnetic reconnection in the corona and the loop prominence phenomenon. Sol. Phys., 1976, 50: 85-98.
[12] H.Hara, T.Kosugi, S.Masuda, Y.Ogawara, S.Tsuneta. A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection. Nature, 1994, 371: 495-497.
[13] D. W.Droemer, H. R.Griem, C. K.Manka, E. A.McLean, B. H.Ripin, J. A.Stamper. Observation of magnetic fields in laser-produced plasma using the Zeeman effect. Phys. Fluids, 1984, 27: 1327-1335.
[14] M.Armengaud, C.Arnas, L.Berge, J.Briand, J. P.Dinguirard, M.El Tamer, A.Gomes, J. C.Kieffer, Y.Quemener. Measurements of magnetic fields using the Zeeman effect in laser-produced plasmas. Phys. Fluids, 1987, 30: 2893-2897.
[15] Y.Abe, Y.Arikawa, H.Azechi, M.Bailly-Grandvaux, S.Fujioka, M.Hata, Y.Iwasa, N.Iwata, T.Johzaki, J.Kawanaka, H.Kishimoto, R.Kodama, S.Kojima, K. F. F.Law, S.Lee, K.Matsuo, K.Mima, N.Miyanaga, A.Morace, H.Morita, H.Nagatomo, M.Nakai, Y.Nakata, H.Nishimura, T.Norimatsu, T.Ozaki, H.Sakagami, S.Sakata, J. J.Santos, H.Sawada, Y.Sentoku, H.Shiraga, T.Shiroto, A.Sunahara, A.Syuhada, S.Tokita, K.Yamanoi, A.Yao, A.Yogo. Magnetized fast isochoric laser heating for efficient creation of ultra-high-energy-density states. Nat. Commun., 2018, 9: 3937.
[17] H.Daido, H.Fujita, M.Fujita, Y.Kitagawa, F.Miki, K.Mima, S.Nakai, K.Sawai, C.Yamanaka. Generation of a strong magnetic field by an intense CO2 laser pulse. Phys. Rev. Lett., 1986, 56: 846-849.
[18] H.Azechi, S.Fujioka, Y.Hironaka, K.Ishihara, T.Johzaki, H.Nakashima, H.Nishimura, K.Shigemori, H.Shiraga, A.Sunahara, T.Watanabe, N.Yamamoto, Z.Zhang. Kilotesla magnetic field due to a capacitor-coil target driven by high power laser. Sci. Rep., 2013, 3: 1170.
[19] Y. Q.Gu, B.Han, S. K.He, W.Hong, F.Li, Y. F.Li, Y. T.Li, G. Q.Liao, C.Liu, F.Lu, X. X.Pei, W. M.Wang, W. W.Wang, H. G.Wei, N.Xie, F. B.Xue, L.Yang, D. W.Yuan, B. H.Zhang, F. Q.Zhang, J.Zhang, K.Zhang, Z.Zhang, G.Zhao, J. R.Zhao, Z. Q.Zhao, J. Y.Zhong, K. N.Zhou, B. J.Zhu, J. Q.Zhu. Strong magnetic fields generated with a simple open-ended coil irradiated by high power laser pulses. Appl. Phys. Lett., 2015, 107: 261903.
[21] Y.Arikawa, H.Azechi, M.Bailly-Grandvaux, C.Bellei, S.Fujioka, S.Kojima, K.Kondo, K. F.Law, S.Lee, K.Matsuo, A.Morace, S.Sakata, J. J.Santos, X.Vaisseau, A.Yogo, Z.Zhang. Direct measurement of kilo-tesla level magnetic field generated with laser-driven capacitor-coil target by proton deflectometry. Appl. Phys. Lett., 2016, 108: 091104.
[22] N.Alfonso, M.Evans, G.Fiksel, W.Fox, L.Gao, H.Ji. Ultrafast proton radiography of the magnetic fields generated by a laser-driven coil current. Phys. Plasmas, 2016, 23: 043106.
[23] Z.Fang, B.Han, N.Hua, W.Jiang, Y.Li, G.Liang, C.Wang, F.Wang, H.Wei, D.Yuan, J.Zhang, Z.Zhang, G.Zhao, J.Zhong, B.Zhu, B.Zhu, J.Zhu. Generation of strong magnetic fields with a laser-driven coil. High Power Laser Sci. Eng., 2018, 6: e38.
[24] Y.He, W.Jiang, Y.Li, Y.Li, J.Ma, J.Tan, J.Wang, Y.Zhang, Z.Zhang, B.Zhu, C.Zhu. Ultrafast pulsed magnetic fields generated by a femtosecond laser. Appl. Phys. Lett., 2018, 113: 072405.
[25] Y.He, W.Jiang, Y.Li, Y.Li, J.Ma, J.Tan, J.Wang, Y.Zhang, Z.Zhang, B.Zhu, C.Zhu. Effects of pulse duration on magnetic fields generated with a laser-driven coil. High Energy Density Phys., 2020, 37: 100900.
[26] Y.Gu, S.He, W.Hong, F.Li, M.Li, Y.Li, Y.Li, G.Liao, F.Lu, W.Wang, X.Wang, N.Xie, L.Yang, B.Zhang, F.Zhang, J.Zhang, Z.Zhang, Z.Zhao, K.Zhou, B.Zhu. Proton radiography of magnetic fields generated with an open-ended coil driven by high power laser pulses. Matter Radiat. Extremes, 2016, 1: 187-191.
[27] J.Chavanne, O.Chubar, P.Elleaume. A three-dimensional magnetostatics computer code for insertion devices. J. Synchrotron Radiat., 1998, 5: 481-484.
[29]
[30] E.Back, F.Paschen. Normale und anomale Zeemaneffekte. Ann. Phys., 1912, 344: 897-932.
[31]
[33] N. V.Abrosimov, E. T.Bowyer, S. K.Clowes, H.Engelkamp, I.Galbraith, H. W.Hübers, J.Li, K. L.Litvinenko, B. N.Murdin, P. G.Murdin, M. L.Pang, S. G.Pavlov, C. R.Pidgeon, H.Riemann. Si:P as a laboratory analogue for hydrogen on high magnetic field white dwarf stars. Nat. Commun., 2013, 4: 1469.
[34] S. F.Anderson, J.Brinkmann, M. J.Collinge, C. C.Dahn, D.Eisenstein, X.Fan, P. B.Hall, H. C.Harris, S.Hawley, S. J.Kleinman, G. R.Knapp, J.Krzesiski, D. Q.Lamb, J.Liebert, B.Margon, A.Nitta, G. D.Schmidt, D. P.Schneider, N.Silvestri, J. A.Smith, P.Szkody. SDSS white dwarfs with spectra showing atomic oxygen and/or carbon lines. Astrophys. J., 2003, 126(5): 2521.
Article Outline
Baojun Zhu, Zhe Zhang, Chang Liu, Dawei Yuan, Weiman Jiang, Huigang Wei, Fang Li, Yihang Zhang, Bo Han, Lei Cheng, Shangqing Li, Jiayong Zhong, Xiaoxia Yuan, Bowei Tong, Wei Sun, Zhiheng Fang, Chen Wang, Zhiyong Xie, Neng Hua, Rong Wu, Zhanfeng Qiao, Guiyun Liang, Baoqiang Zhu, Jianqiang Zhu, Shinsuke Fujioka, Yutong Li. Observation of Zeeman splitting effect in a laser-driven coil[J]. Matter and Radiation at Extremes, 2022, 7(2): 024402.



