1. INTRODUCTION

Ghost imaging (GI) has been an active research topic in recent years ^{[1–37" target="_self" style="display: inline;">–37]}. Depending on the spatial correlation properties of fluctuating light fields (either thermal or entangled), researchers can divide the source into two correlated beams and send one of them through a test path, which contains an unknown test object, and the other through a reference path having no interaction with the test object. An image of the object can be obtained from the correlation measurement between the intensity recorded in the test and reference detectors. Historically, entangled two-photon (or biphoton) states were first used to generate a ghost image via coincident measurement, and the entanglement properties are claimed to be the key factor to realize GI. However, further studies revealed that classically incoherent light sources also can be used to realize GI. Since then, there have been a lot of works on classical GI.

Recently, we have followed the idea of GI to investigate light scattering with classically correlated light sources ^[38]. In our work, we use the scatterers to replace the objects in the GI scheme and place the detectors far from the scatterers to collect the scattering data. We also perform nonlocal correlation measurement of the differential scattering cross-section fluctuations in the test and reference paths, and then we find that the scattering information of the test scatterer can be obtained in the reference arm with the help of a fixed point-like detector in the test arm, just like the case in GI. It is natural to ask whether and how entangled light sources can be used in the research of ghost scattering. The purpose of this paper is to present a theoretical analysis of the quantum ghost scattering with biphoton quantum states.

In fact, there already exists some literature on light scattering with quantum light sources ^{[39–43" target="_self" style="display: inline;">–43]}. Notably, Schotland et al. ^[43] used the formal scattering theory to study the scattering of biphoton states from collections of small particles, paying special attention to the variation of quantum correlation properties when the light is scattered by only one scatterer. Instead, here we will use the mathematical tools in ^[43] to study how biphoton ghost scattering patterns can be formed when two optical paths are involved.

The paper is organized into four sections. In Section 2, we give the theoretical description on biphoton ghost scattering from the formal scattering theory. We present numerically simulated results in Section 3. Conclusions are given in Section 4.

2. BIPHOTON GHOST SCATTERING THEORY

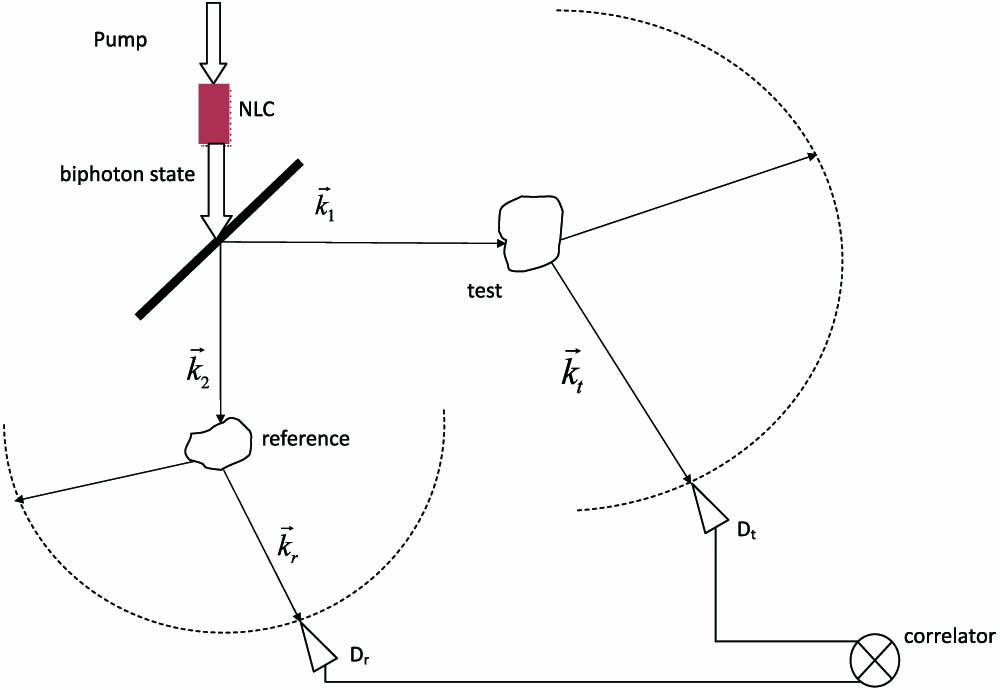
We show a typical biphoton ghost scattering configuration in Fig. 1. Just like in the case of an entangled photon GI, a nonlinear crystal is pumped by an incident laser beam to generate entangled photon pairs. These biphoton states then are separated in space by a beam splitter. The output test and reference photons are entangled in propagating directions and travel in two paths: the test path and reference path. In the test path, the test photons are scattered by an unknown test object and are detected by a point-like detector Dt. In the other reference path, we place a known object as a reference scatterer and measure the scattered reference photons from this scatterer via a point-like detector Dr. As done in the GI experiments, Dt and Dr can be scanned over a large enough space, and we can use the coincidence measurement to obtain the second-order coherence function Γ(2)(x→t,x→r)=⟨ψ|E^−(x→t)E^−(x→r)E^+(x→r)E^+(x→t)|ψ⟩ (with E^± the positive/negative frequency component of the electric-field operator). We will show that the scattering information of the unknown test object can be retrieved from this kind of coherence function.

Fig. 1. Geometry of a biphoton ghost scattering system. A pump beam illuminates a nonlinear crystal (NLC) to generate the biphoton quantum states. The biphoton state is then split by a beam splitter, leading to the separation of the test and reference photons (with wave vectors k→1,2). The test photon illuminates an unknown object and is scattered into the far field, measured by the test detector located at x→t. The other reference photon is scattered by a known reference object and collected by the reference detector Dr at x→r. Corresponding wave vectors of the scattered photons are k→t and k→r. The second-order coherence function can be measured by the correlator.

下载图片 查看所有图片

The initially incident biphoton quantum state can be described by where a^x→† (a^k→†) is the creation operator in the real space (momentum space), Ai(x→,ω;x→′,ω′) and Ai(k→,k→′) are the two-photon amplitude of the incident field in the real space and momentum space, connected by Ai(x→,ω;x→′,ω′)=∫dk→dk→′exp{i(k→·x→+k→′·x→′)}Ai(k→,k→′). For simplicity, we have assumed the test and reference photons are monochromatic, with frequency ω and ω′.

Following ^[43], in the real space, the two-photon amplitude of the scattered field can be obtained by the T-matrix method: where Gt and Gr are the free Green’s function in the test and the reference paths, corresponding to the wavenumber kt=ω/c and kr=ω′/c, with the formula G(x→,x→′)=eik|x→−x→′||x→−x→′|. Tt and Tr are the T-matrices characterizing the light scattering processes in the test and the reference paths and obey the integral equation: where s=r,t corresponding to the reference or test paths, and the susceptibility η relates to the dielectric permittivity ε via ε=1+4πη.

Denote x→=xx^ (x^ is a unit vector to specify the position vector x→), in the far-field limit (x≫x′), G(x→,x→′)∼ejkxxe−jkx^·x→′, then we have in which k→t=ktx^, k→r=krx^′, |k→t|=|k→|=ω/c, |k→r|=|k→′|=ω′/c, and are the T-matrices in the momentum space. We have introduced the symbols to describe the far-zone scattered field.

Suppose the photons scattered by the test object are detected by the test detector at a direction k→t, and the photons scattered by the reference object are detected by the reference detector at another direction k→r, the ghost scattering signals will be proportional to the second-order coherence function of the scattering states, corresponding to the probability of simultaneously detecting one scattered photon at the test detector and a second scattered photon at the reference detector. Because only biphoton states are considered, the second-order coherence function is factorable and can be represented as the modular square of the two-photon amplitude, |As(x→,ω;x→′,ω′)|2. With the help of Eq. (4), in the following parts, we define G(k→t,k→r)=|As(k→t,k→r)|2 as the correlated scattering signal to describe the properties of biphoton ghost scattering, which can be written as

It is clear that, if the incident quantum state is fully entangled, Ai(k→,k→′)∝δ(k→−k→′), then G(k→t,k→r)=|∫dk→T(k→t,k→)R(k→r,k→)|2 is determined by the test and reference scattering channels in a non-separable form. Especially, if the reference object is carefully designed so that R(k→r,k→)≈δ(k→r−k→), then G(k→t,k→r)≈|T(k→t,k→r)|2, which means that, if we fix a test detector in a given direction (k→t), the scattering information of the test object can be obtained from the reference path (as the function of k→r), showing the similar nonlocal feature as in the case of ghost imaging.

To analyze the properties of the ghost scattering with biphoton states, we assume the two-photon amplitude of the incident field Ai takes the form where the δ function means the test and reference photons are strictly entangled in momentum, and the envelop function U represents that the photons have a distribution of propagating directions.

In the following parts, for the incident states in Eq. (6), we can discuss two kinds of correlated scattering signals, Gt and Gr, as in ^[38] corresponding to the scattering in the test path with a fixed detector in the reference path (k→0), which may be called a direct scattering pattern because the scattering signal seems to emerge directly from the path in which the unknown test scatterer exists, and corresponding to the scattering in the reference path with a fixed detector in the test path (k→0), so that we call it a ghost scattering pattern because now the scattering signal is a function of the reference directions, which seem to have no relation to the test object.

3. NUMERICAL SIMULATIONS

When the susceptibility distributions of the test and reference objects are known, we can directly solve Eq. (3) and Eqs. (7) and (8) to simulate the biphoton ghost scattering patterns. It is well known that rigorous results exist for the T-matrix of certain objects, such as the point-like scatterers or the homogeneous spherical scatterers. Just like in ^[43], we will use these two kinds of objects to demonstrate our biphoton ghost scattering theory.

In the following simulations, we place a collection of identical small point-like scatterers as the reference object in the reference path, and a homogeneous spherical scatterer as the test object in the test path. For simplicity, we suppose the photons in both test and reference have the same frequency, ω=ω′. The test sphere is assumed to have a radius ka=5 centered at the origin of the test path and the index of refraction n=1.5, so that the T-matrix can be calculated from the Mie coefficients ^[43]. The reference object is composed by 2D 27×27 point scatterers, with radius ka=0.2 and refractive index n=1.5. The T-matrix of such an object can be obtained from the formulas in ^[43]. In our case, the point scatterers are periodically placed with the nearby distances in both x and y directions kd=1. We further assume the incident biphoton state is described by Eq. (6), with the envelop function for three different values of α=0.04,0.2,0.6, corresponding to small-, medium-, and large-sized incident states.

For the test sphere object, choosing k→i=(0,0,k) and k→=(kx,ky,k2−kx2−kz2), the forward distribution of the corresponding T-matrix, |T(k→,k→i)|2, has been shown in Fig. 2(a). It is clear to see the symmetry of the scattering signals around the central direction. In Fig. 2(b), we plot the forward T-matrix distribution of the reference object, |R(k→,k→i)|2 (with k→i=(0,0,k) and k→=(kx,ky,k2−kx2−kz2)). The periodically distributed 2D point scatterers lead to some sharp peaks, just like in the case of the Bragg diffraction. Actually, if we increase the number of point scatterers used in this example, the size of these scattering peaks will be decreased, and R(k→r,k→) will be close to a set of δ functions with a maximum central peak, i.e., R(k→r,k→)≈δ(k→r−k→).

Fig. 2. (a) T-matrix of the test object |T(k→,k→i)|2. (b) T-matrix of the reference object |R(k→,k→i)|2. (c), (e), and (g) Direct scattering patterns Gt(k→) for the small-, medium-, and large-sized incident states. (d), (f), and (h) Ghost scattering patterns Gr(k→) for the small-, medium-, and large-sized incident states. Detailed explanations and parameters are given in the main text.

下载图片 查看所有图片

In Figs. 2(c), 2(e), and 2(g), for three kinds of incident states (corresponding to α=0.04,0.2,0.6), we present the direct scattering patterns Gt(k→) [defined by Eq. (7)] as the function of (kx,ky) with a fixed reference direction k→0=(0,0,k). We find for all three kinds of envelop functions we used in simulations, the direct scattering patterns Gt(k→) have almost the same structures and are close to the T-matrix of the test object in Fig. 2(a). The reason can be seen in Eq. (7). Because we can approximate R(k→0,k→i) as a function δ(k→0−k→i) and k→0 is a fixed vector, then in the integral U(k→i)δ(k→0−k→i)=U(k→0)δ(k→0−k→i), so that the size of envelop function has little effect on the structures of the direct scattering patterns Gt(k→).

On the other hand, in Figs. 2(d), 2(f), and 2(h), we plot the ghost scattering patterns Gr(k→) [defined by Eq. (8)] as the function of (kx,ky) with a fixed test direction k→0=(0,0,k). Clearly we see the change of the structures with the variation of the size of the incident states. For a small-sized state [α=0.04 in Fig. 2(d)], the ghost scattering pattern looks similar to the original T-matrix of the reference object [Fig. 2(b)]; even the tiny outer spots can be resolved, though there are certain quantitative differences. This figure can be interpreted from Eq. (8). Here, U(k→i) is not zero only at a very small region; thus we may regard it as a function δ(k→i−k→0). Also k→0 is fixed, so that the integral will lead to |T(k→0,k→0)|2·|R(k→,k→0)|2, proportional to the T-matrix of the reference object, as shown in Fig. 2(d).

For a large-sized state [α=0.6 in Fig. 2(h)], the ghost scattering pattern looks like the T-matrix of the reference object [Fig. 2(a)]. Here, because U(k→i) is very large, we may approximate it as 1 and approximate R(k→,k→i) as δ(k→−k→i). Then from Eq. (8), we find the ghost scattering pattern Gr should be proportional to the T-matrix of the test object. Of course, due to the imperfections of these approximations, some detailed structures may be lost in Fig. 2(h), such as the outer-most ring. For the medium-sized state [α=0.2 in Fig. 2(f)], there does not exist an intuitive explanation. From the numerical results, we can say now that the ghost scattering pattern Gr lies between Figs. 2(d) and 2(h) and represents a kind of crossover.

Finally, we would like to compare the quantum ghost scattering scheme in this work with the classical ghost scattering theory in ^[38]. Although the thermal light field and biphoton states can be used in a ghost scattering scheme to obtain the scattering information of the test scatters, there are two main distinctions. First, in classical ghost scattering, there exists background terms, so that we need to calculate the fluctuation correlation to retrieve the scattering information. On the other hand, due to the structure of the biphoton wave function [Eq. (1)], there is no background in the biphoton ghost scattering scheme. Second, the correlated scattering signal [Eq. (5)] in the biphoton scattering scheme is related to the product T(k→t,k→)R(k→r,k→′), while for the classical ghost scattering scheme, it should be T(k→t,k→)R*(k→r,k→′). This difference of the conjugate term can be contributed to the different statistical properties of the thermal light field and biphoton states and may be found in applications in the study of phase-sensitive scatterers.

4. CONCLUSION

In conclusion, we have performed a theoretical analysis of the quantum ghost scattering scheme in which the biphoton quantum states have been used. Our work generalizes the previously reported ghost scattering theory with classically incoherent sources. We have derived exact formulas for the correlated scattering signals based on the formal quantum scattering theory. We find that the scattering information of a test object can be obtained in either the test arm or the reference arm. For a carefully designed reference object, numerical results show that the scattering patterns obtained in the reference arm may be changed from the T-matrix of the test object to the T-matrix of the reference object by adjusting the size of the biphoton states.