具有2<i>n</i>+1次非线性的薛定谔方程暗孤子特性

周昱; 张远; 王颖; 赵明琳; 闫东广

doi:doi:10.3788/AOS202040.0927001

光学学报, 2020, 40 (9): 0927001, 网络出版: 2020-05-06

具有2n+1次非线性的薛定谔方程暗孤子特性下载： 934次

Dark Soliton Properties of Nonlinear Schrödinger Equation with (2n+1)-th Order Nonlinearity

论文大纲

周昱 ^1,*张远 ¹王颖 ¹赵明琳 ¹闫东广 ²

作者单位

¹ 江苏科技大学理学院, 江苏镇江 212003

² 江苏科技大学材料科学与工程学院, 江苏镇江 212003

量子光学孤子非线性薛定谔方程相位 quantum optics soliton nonlinear Schr?dinger equation; phase

AI 词云图 AI语音精读 AI语音超短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

研究了具有2n+1次非线性的薛定谔方程暗孤子特性。首先,给出了静态暗孤子解的统一解析表达式,发现静态暗孤子的宽度随非线性幂次的增大而减小,其深度保持不变。其次,研究了运动暗孤子的演化行为,给出了运动暗孤子波函数随空间和时间变化的普适表达式,发现对于给定的暗孤子运动速度,孤子的密度和相移都随非线性幂次的增加而减小。研究结果表明,对于给定的非线性多方指数,运动暗孤子的能量随运动速度的增加而减小。最后,通过数值模拟验证了所得解析结果。

Abstract

We study the properties of dark solitons of the nonlinear Schr?dinger equation with (2n+1)-th order nonlinearity. We give the uniform analytical expression for a static dark soliton and find that the width of the static dark soliton decreases with the increase of the nonlinear power index, and its depth remains unchanged. The evolution behavior of the moving gray soliton is studied, and the general expression of the wave function of the moving gray soliton as a function of space and time is given. It is found that if we give the speed of a moving gray soliton, the density and phase shift decrease as the nonlinear power index increases. The energy of the moving gray soliton decreases with the increase of its speed for a given nonlinear power index. Finally, the numerical simulation is given to verify the analytical results.

1 引言

非线性薛定谔方程(NLSE)是描述物理系统中非线性问题的一个重要工具,被广泛地应用于各种非线性现象研究中,例如光纤和波导中的非线性光脉冲、锁模激光、光折变材料中的光传播、超冷原子体系(包括超冷玻色气体和费米气体)中的非线性物质波、等离子体中的非线性电磁脉冲等,具有重要的科学意义和应用价值^[1-2]。对NLSE的研究,不仅有助于研究者从物理层面揭示体系内在的物理机制并给出有关数学结论的合理解释,还有助于研究者通过从数学上得到的某些结论来预言新的物理现象或结果^[3-5]。

NLSE涉及种类丰富的非线性局域解,在这些解中,最重要的一类是孤子解。孤子是一类能在传播过程中保持波形和运动速度不变的波包,是由方程中的色散或衍射与非线性相互作用所产生的^[6]。孤子的特性一直受到人们的广泛关注。孤子的分类有很多种,通常把孤子中心密度大于系统背景密度的称为亮孤子,小于背景密度的称为暗孤子。对于暗孤子,如果其中心密度为零,可称为黑孤子,中心密度不为零的则为灰孤子。一般认为黑孤子是静态的,位置不随时间改变,而灰孤子的位置随时间变化^[7]。

随着实验技术的发展,人们已经观察到单个孤子^[8-12]、涡旋孤子^[13-16]、环状孤子^[17-19]、X-型孤子等不同类型的孤子。除单个孤子外,研究者可以一次性制备多个孤子,例如孤子对^[20]、孤子链^[21]、孤子分子^[22]等。以超冷原子气体为例,人们利用相位刻印技术^[23-24],通过调节磁场,在原子玻色-爱因斯坦凝聚体(BEC)和超流费米气体中相继实现了亮、暗孤子^[25-28] 。此外,在多组分(具有不同自旋分量)BEC中也实现了矢量孤子^[29-31]。

随着研究的深入,人们发现对于某些物理体系而言,常用的立方非线性薛定谔方程已经难以描述或预言有关物理现象,例如超冷原子气体中两体以上的相互作用,光脉冲在里德堡共振原子介质中的传播等。在这些情况下低阶非线性效应不足以描述体系的物理机制,需要引入高阶非线性。事实上,将非线性薛定谔方程的形式在数学上进行一般性推广,使非线性项不只是3次方形式,而是任意2n+1次多方形式,这样该方程就可以描述某些特殊情况下普通的立方非线性薛定谔方程所不能描述的物理现象^[32-36],在这些情况下,针对不同体系,不同的非线性多方指数可代表不同的物理过程。

本文利用推广的具有2n+1次非线性的薛定谔方程来描述暗孤子的演化,分静态孤子和运动孤子两种情况分别讨论。给出了理论框架并考察了静态孤子的波函数和密度分布;给出了运动孤子动力学并进行了密度计算和相位演化。研究结果表明,运动孤子的表达式在不同的多方指数下可以用一个统一的形式来表达。并给出了孤子能量随多方指数和孤子运动速度的变化关系。

2 非线性薛定谔方程和静态暗孤子

非线性薛定谔方程不仅可以用于求解基态问题,也可以用于处理激发态问题。如果外势的径向束缚足够强,该方向的激发被抑制,则孤子只能在轴向上产生和运动,这时,NLSE可写为准一维形式:

i ћ \frac{\partial Ψ_{1 D} (x, t)}{\partial t} = - \frac{ћ^{2}}{2 M} \frac{\partial^{2} Ψ_{1 D} (x, t)}{\partial x^{2}} + V_{ext} (x) Ψ_{1 D} (x, t) + g | Ψ_{1 D} (x, t) |^{2 n} Ψ_{1 D} (x, t), (1)

式中:Ψ_1D(x,t)为波函数;x为坐标;t为时间;n为多方指数;M, ћ是常数;g是描述非线性相互作用的参量,一般与正整数n有关;V_ext(x)是谐振子外势,一般不含时。如果n=1,则(1)式变为普通的NLSE。如前述,不同的n代表不同的非线性物理过程。 (1)式孤子解的稳定性已由Vakhitov-Kolokolov判据给出^[37-38]。准一维要求激发的尺度远小于体系的轴向尺度,径向无能量跃迁,也就是在y和z方向只存在基态而没有激发态。反之,如果轴向激发的尺度和体系本身的轴向尺度可比拟,那么就必须考虑涨落因素。如果外势很弱,可以忽略,则(1)式变为

i ћ \frac{\partial Ψ_{1 D} (x, t)}{\partial t} = - \frac{ћ^{2}}{2 m} \frac{\partial^{2} Ψ_{1 D} (x, t)}{\partial x^{2}} + g | Ψ_{1 D} (x, t) |^{2 n} Ψ_{1 D} (x, t), (2)

式中:m是常数。如果波函数可写成Ψ_1D(x,t)=ψ(x)exp(-iμt/ћ)(ψ(x)为不含时波函数,μ为化学势),且μ由归一化条件决定,则(2)式又可简化。

静态暗孤子即黑孤子,其波函数不含时,是一种静态结构,取ћ=m=1,可将(2)式重写为

- \frac{1}{2} \frac{\partial^{2} ψ (x)}{\partial x^{2}} + g ψ^{2 n + 1} (x) = μψ (x), (3)

(3)式的本征能量最低值对应基态。如果限定(3)式解的形式为实函数,则黑孤子解在拓扑上是稳定的,波函数解的形式是一个纽结,且零点处的密度为零、具有-π跃变相位。从物理角度来看,如果x→±¥,则实函数ψ(x)具有有限值± $\sqrt[]{ρ_{0}}$ ,其中ρ₀为原子数密度。对于无外势的均匀体系,由(3)式易得出μ=g|ψ(x)|²ⁿ=g $ρ_{0}^{n}$ 。

将(3)式改写为

\frac{1}{2} \frac{\partial^{2} ψ}{\partial x^{2}} = - μψ + g ψ^{2 n + 1}, (4)

(4)式在形式上等同于在外势V(ψ)中运动的质量为1/2的质点的牛顿方程。(4)式等号右边对ψ直接积分,可以得到V(ψ)=μψ²/2-gψ²ⁿ⁺²/(2n+2)+C,其中C是积分常数。可以发现,运动常数E为

E = \frac{1}{4} {(\frac{\partial ψ}{\partial x})}^{2} + V (ψ) 。 (5)

当ψ趋近于 $\sqrt[]{ρ_{0}}$ 时,∂V/∂ψ的值应该等于零,所以可定出积分常数 C=-μρ₀/2+g $ρ_{0}^{n + 1}$ /(2n+2),这便要求E=0。重新整理(5)式并化简可得

\frac{\partial ψ}{\partial x} = \sqrt[]{\frac{2 g}{n + 1}} (ψ - \sqrt[]{ρ_{0}}) (ψ + \sqrt[]{ρ_{0}}) \sqrt[]{p_{2 n} (ψ)}, (6)

式中:多项式p₂_n(ψ)= $\overset{n - 1}{\sum_{j = 0}}$ (n-j)ψ²^jρⁿ^-1-^j总是大于零;ψ(x)在x=0处有一个节点,是一个实的奇函数,并且有0<ψ< $\sqrt[]{ρ_{0}}$ ,这里粒子数密度ρ(x)=ψ²(x)。需要注意的是,把ψ取为实函数的目的是为了在物理上保证不出现粒子流。

现在考虑最简单的n=1和n=2的暗孤子情况。对于n=1,V(ψ)的表达式是V(ψ)=-g(ψ- $\sqrt[]{ρ_{0}}$ )²(ψ+ $\sqrt[]{ρ_{0}}$ )²/4,且波函数ψ应该满足方程∂ψ/∂x= $\sqrt[]{g}$ (ψ- $\sqrt[]{ρ_{0}}$ )(ψ+ $\sqrt[]{ρ_{0}}$ ), 如果考虑边界条件ψ(0)=0和ψ(¥)= $\sqrt[]{ρ}$ ,则可以通过直接积分给出ψ的表达式为

ψ (x) = \sqrt[]{ρ_{0}} \tanh (\sqrt[]{g ρ_{0}} x) 。 (7)

(7)式是一个静态解,其对应的孤子速度为零。解的空间形式是一个纽结,波函数的相位在原点有一个-π跃变。

对于n=2,可以看出(3)式具有五次非线性,V(ψ)=-g(ψ- $\sqrt[]{ρ_{0}}$ )²(ψ+ $\sqrt[]{ρ_{0}}$ )²(ψ²+2ρ₀)/6,且波函数ψ随x的变化满足∂ψ/∂x= $\sqrt[]{2 g / 3}$ (ψ- $\sqrt[]{ρ_{0}}$ )(ψ+ $\sqrt[]{ρ_{0}}$ ) $\sqrt[]{ψ^{2} + 2 ρ_{0}}$ 。通过直接积分并考虑边界条件,可得

ψ (x) = \sqrt[]{2 ρ_{0}} \frac{\tanh (\sqrt[]{2 g} ρ_{0} x)}{\sqrt[]{3 - \tan h^{2} (\sqrt[]{2 g} ρ_{0} x)}} 。 (8)

这里得到的孤子性质可类比为上述n=1的情况。

进而考虑n=3的情况,得到一个关于ψ的方程:

\frac{\partial ψ}{\partial x} = \sqrt[]{\frac{g}{2}} (ψ - \sqrt[]{ρ_{0}}) (ψ + \sqrt[]{ρ_{0}}) \sqrt[]{ψ^{4} + 2 ρ_{0} ψ^{2} + 3 ρ_{0}^{2}} 。 (9)

明显看出,(9)式在数学上无法通过直接积分得到一个关于ψ的初等函数表达式。与n=3的情况类似,n>3时也无法通过直接积分给出一个初等函数表达式。

现在尝试用一个统一的形式来研究n≥3的情况。由(6)式可写出积分

\overset{ψ (x)}{\int_{0}} \frac{d ψ}{(ψ - \sqrt[]{ρ_{0}}) (ψ + \sqrt[]{ρ_{0}}) \sqrt[]{p_{2 n} (ψ)}} = x \sqrt[]{\frac{2 g}{n + 1}}, (10)

(10)式在形式上是一个超椭圆积分,无法直接给出积分值^[39]。现令b(x)≡ψ(x)/ $\sqrt[]{ρ_{0}}$ ,得到

x \sqrt[]{\frac{2 g ρ_{0}^{n}}{n + 1}} = \overset{b}{\int_{0}} \frac{d b}{\sqrt[]{n - [(n + 1) b^{2} - b^{2 n + 2}]}} 。 (11)

计算并整理可得到有关x的表达式:

\begin{array}{r} x = f (b) = & \frac{1}{2 \sqrt[]{n + 1}} \overset{\infty}{\sum_{k = 0}} \frac{1}{k!} \frac{Γ (q_{k} + k)}{Γ (q_{k} + 1)} {[\frac{n^{n}}{{(n + 1)}^{n + 1}}]}^{k} {[\frac{(n + 1 - b^{2 n}) b^{2}}{n}]}^{q_{k}} \times_{2} F_{1} [q_{k}, \frac{1}{2}, q_{k} + 1; \frac{(n + 1 - b^{2 n}) b^{2}}{n}], (12) \end{array}

式中:k为求和指标;Γ(·)为伽马函数;₂F₁(·)为高斯超几何函数;q_k为与n有关的参数,q_k=(2nk+1)/2。(12)式等号右边最后一项是高斯超几何函数^[40], 通过(12)式可以写出波函数ψ(x)的解析式为ψ(x)= $\sqrt[]{ρ_{0}}$ f^-1(x),f^-1(x)为f(x)的反函数,可以看出,ψ(x)仅在n<3的情况下是初等函数表达式,并且很容易证明,当n为1、2时,ψ(x)的解析表达式正是(7)式和(8)式。

图1给出了波函数ψ(x)和孤子的密度ψ²(x)随空间x的变化关系,这里取g=1和ρ₀=1。我们发现孤子的波函数及密度有一个渐近行为。波函数纽结在通过点x=0时改变了符号,相位跃变-π,且密度的最小值总是为零。进一步计算发现,孤子的宽度随着多方指数的增加而减小,这表明体系非线性效应的增强使得孤子的密度分布变得更加集中。将这里的结论和由Bogoliubov-de Gennes方程得到的超流费米气体的有关结论^[41]进行对比,发现两者计算的结果一致。研究表明,文献[ 41]考虑了体系非凝聚部分的量子耗尽效应,得到的波函数和密度在尾部有一个振荡行为且最小密度在某些区域不为零,而本文非线性薛定谔方程的使用前提条件是所有的粒子都处于宏观相干态。

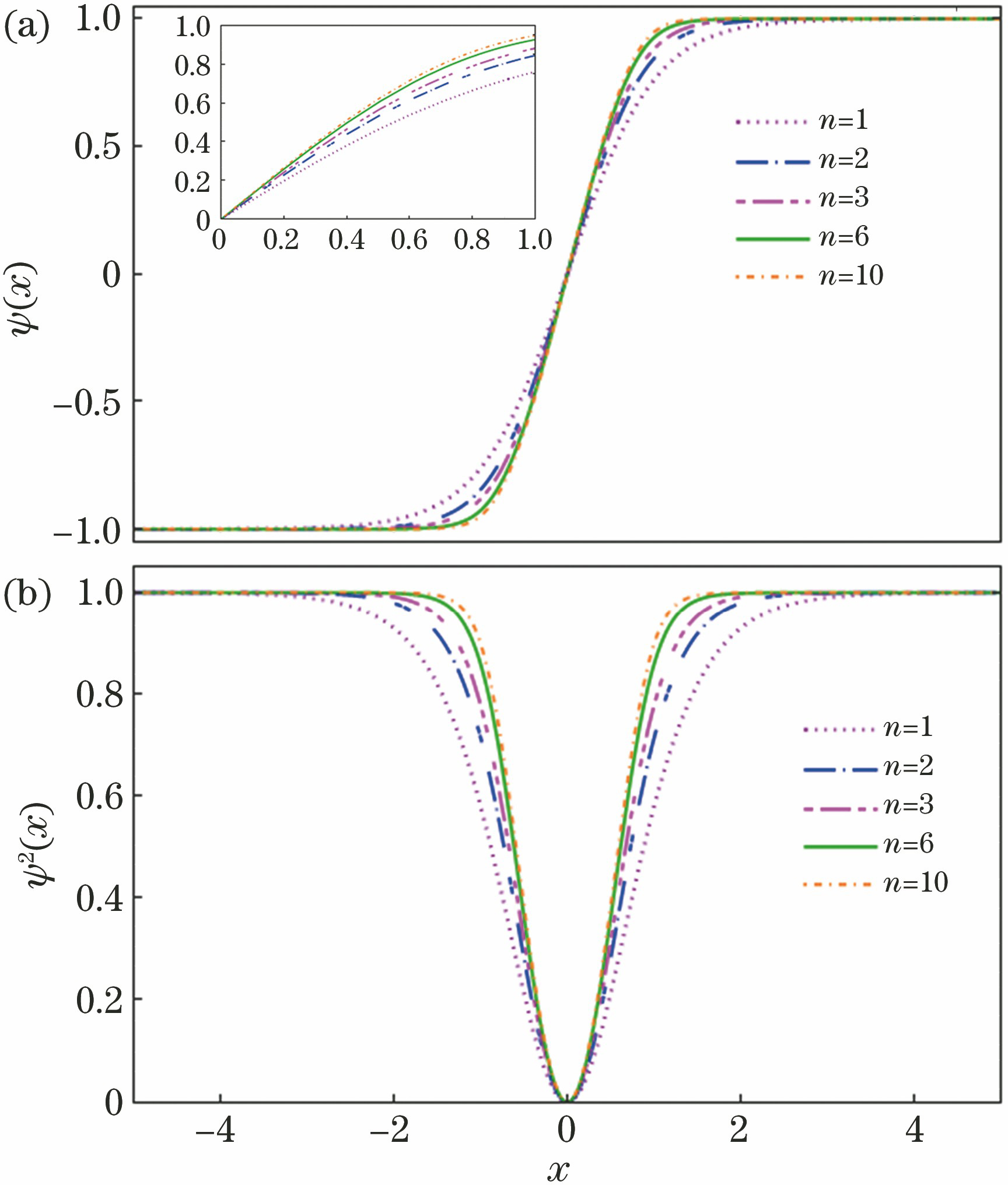
图 1. 静态暗孤子的波函数和粒子数密度在不同n下随x的变化。(a)波函数,插图是孤子波函数的局部放大;(b)粒子数密度

Fig. 1. Evolution of wave function and particle number density of static dark soliton with x for different n. (a) Wave function with its local magnification shown in inset; (b) particle number density

下载图片查看所有图片

进一步研究发现,波函数在x=0处的斜率随多方指数变化,也就是n越大,斜率就越大并最终趋近于固定值。这个结论很有趣,在数学上多方指数虽然可以一直增加,但x=0处的波函数斜率却并未随之线性增加,这是由于体系粒子间的非线性相互作用。

3 运动暗孤子

除了上一节研究的静态孤子解之外,含时(2)式还允许具有速度v的孤子解,其随空间和时间演化,定义ζ=x-vt,ћ=M=1,(2)式变为

- i \frac{\partial Ψ_{1 D}}{\partial ζ} = - \frac{1}{2} \frac{\partial^{2} Ψ_{1 D}}{\partial ζ^{2}} + g | Ψ_{1 D} |^{2 n} Ψ_{1 D} 。 (13)

记波函数Ψ_1D(x,t)=ψ(ζ)exp(-iμt)=ϕexp(iθ)·exp(-iμt),ζ依赖于实函数振幅ϕ和相位θ,代入(13)式可得一组关于振幅ϕ和相位θ的耦合方程,即

\{\begin{array}{l} \frac{1}{2} ϕ ″ = - μϕ - vϕθ' + \frac{1}{2} ϕθ'^{2} - g ϕ^{2 n + 1} \\ vϕ' = ϕ' θ' + \frac{1}{2} ϕθ ″ \end{array} 。 (14)

当ϕ非零时,(14)式中的第二个方程可写为

v (ϕ^{2})' = (ϕ^{2} θ')', (15)

可得关于相位θ的导数为

θ' = v (1 - \frac{c}{ϕ^{2}}), (16)

式中:c是积分常数。将(16)式代入(14)式中的第一个方程,得到

\frac{1}{2} ϕ ″ = - μϕ - v^{2} ϕ (1 - \frac{c}{ϕ^{2}}) + \frac{1}{2} v^{2} ϕ {(1 - \frac{c}{ϕ^{2}})}^{2} + g ϕ^{2 n + 1} 。 (17)

(17)式也可描述质量为1/2的粒子在外势中的运动。因此

V (ϕ) = \int (μϕ + \frac{1}{2} v^{2} ϕ - \frac{v^{2} c^{2}}{2 ϕ^{3}} - g ϕ^{2 n + 1}) d ϕ = \frac{1}{2} μ ϕ^{2} + \frac{v^{2}}{4} (ϕ^{2} + \frac{c^{2}}{ϕ^{2}}) - \frac{g}{2 n + 2} ϕ^{2 n + 2} + C_{g}, (18)

式中:积分常数C_g待确定。与处理(5)式的思路类似,可得到E=0。令原子数密度ρ₀=1,则V(1)=0,可给出C_g=-μ/2-v²(1+c²)/4+g/(2n+2)。

由前述n=1的情况可知,在ζ=0处的暗孤子解是一个纯虚数iv/s,其中声速s和愈合长度 ξ=ћ/ $\sqrt[]{2 mg ρ_{0}}$ 的关系是mvξ/ћ=v/ $\sqrt[]{2}$ s。可以算出,当波函数振幅ϕ取两个值的时候可满足V(ϕ)=0,其中一个值ϕ= $\tilde{ϕ}$ = $\sqrt[]{ρ_{0}}$ ,且当 ρ₀=1时 $\tilde{ϕ}$ 为1。对于n=1的情况,得到

V_{n = 1} (\tilde{ϕ}) = \frac{1}{4} (v^{2} - g) (1 - c^{2}), (19)

可得常数c=±1,取c=1并进而求出常数C_g。这里给出V(ϕ)的表达式为

V (ϕ) = \frac{1}{2} μ ϕ^{2} + \frac{v^{2}}{4} (ϕ^{2} + \frac{1}{ϕ^{2}}) - \frac{g}{2 n + 2} ϕ^{2 n + 2} - \frac{1}{2} μ - \frac{v^{2}}{2} + \frac{g}{2 n + 2} 。 (20)

由于

\frac{1}{4} {(\frac{\partial ϕ}{\partial ζ})}^{2} + V (ϕ) = 0, (21)

可以得到积分

\overset{ϕ (t)}{\int_{\tilde{ϕ}}} \frac{d ϕ}{\sqrt[]{- 4 V (ϕ)}} = \overset{ζ}{\int_{0}} d ζ 。 (22)

考虑到已经选取μ=g,则得

ζ = \overset{ϕ}{\int_{\tilde{ϕ}}} \frac{d ϕ}{\sqrt[]{2 (\frac{ng}{n + 1} + v^{2}) - 2 g ϕ^{2} - v^{2} (ϕ^{2} + \frac{1}{ϕ^{2}}) + \frac{2 g}{n + 1} ϕ^{2 n + 2}}} 。 (23)

当v=0时,(23)式为上一节静态孤子解,且根号下的表达式为2g{n-[(n+1)ϕ²]-ϕ²ⁿ⁺²}/(n+1),此时的积分下限为零。

图2给出了灰孤子密度ϕ²和相位θ在不同n下随ζ的变化,选取v/s=0.8。从图2可知:1)随着n的增加,孤子中心密度增加;2)孤子的宽度在n=1时最小且随n的增大而增大,这反映出粒子间的非线性相互作用的变化;3)当ζ=0时,相位有一个连续变化但不是跃变,这与黑孤子的情况相反,随着n的增加,ζ=0点附近的相位变化逐渐减小;4)n越大,相位变化越不明显,这与密度的变化趋势是一致的。

图 2. v=0.8s时灰孤子的粒子数密度和相位在不同n下随ζ的变化。(a)粒子数密度;(b)相位

Fig. 2. Variation of particle number density and phase of gray soliton with ζ for different n at v=0.8s. (a) Particle number density; (b) phase

下载图片查看所有图片

孤子可以具有不同的运动速度,这和体系中的声速是直接相关的。研究结果表明:1)v=0时孤子的中心密度为零,而除此之外中心密度皆不为零,当v=s时,孤子和背景融为一体;2)孤子宽度随v的增加而增加,当v=s时,孤子的宽度无穷大,此时在物理上认为孤子已经消失,因为孤子的性质保证了体系中产生的孤子的速度不能超过体系的声速;3)相位变化随孤子速度的增加而逐渐减小, v=0时ζ=0处的孤子相位有-π的跃变,v=s时孤子消失。

对于n=1的情况,灰孤子解已知,形如

Ψ_{1 D} (x, t) = \sqrt[]{ρ_{0}} [i \frac{v}{s} + β \tanh (βsζ)] \exp (- i μt), (24)

式中:β为系数,β= $\sqrt[]{1 - v^{2} / s^{2}}$ 。假设任意n时的灰孤子解为

Ψ_{1 D} (x, t) = ψ_{ans} (ζ) \exp (- i μt) = \sqrt[]{ρ_{0}} f_{n} (ζ) [i \frac{v}{s} λ_{n} + \sqrt[]{1 - \frac{v^{2}}{s^{2}} λ_{n}^{2}} Φ_{n} (βsζ)] \exp (- i μt), (25)

式中:ψ_ans(ζ)为拟设的波函数;f_n(ζ)和Φ_n(ζ)是实函数;λ_n是不依赖于ζ的参数。 n=1时,(25)式可以约化为(24)式,且λ₁=1,f₁=1, Φ₁=tanh(βsζ),v=0时黑孤子解为 $\sqrt[]{ρ_{0}}$ Φ₁。(25)式中的参数λ_n由相位差确定,即

θ (ζ) = \arctan \frac{\frac{v}{s} λ_{n}}{\sqrt[]{1 - \frac{v^{2}}{s^{2}} λ_{n}^{2}} Φ_{n}} - \frac{π}{2} 。 (26)

当ζ→±¥时Φ_n为1,故

λ_{n}^{2} = \frac{s^{2}}{v^{2}} \frac{ta n^{2} (θ + π / 2)}{1 + ta n^{2} (θ + π / 2)} 。 (27)

当ζ→¥时,θ有一个渐近值。利用λ_n,可以立刻得出 $f_{n}^{2}$ 和 $Φ_{n}^{2}$ 。利用f_n和Φ_n,可把任意多方指数下的灰孤子解表示为一个统一的形式,含λ_n的虚部可以利用相位差求解。计算结果表明, $Φ_{n}^{2}$ 的宽度随n的增加而减小,且中心密度为零,其原因与前述一致;当n=1时, $f_{n}^{2}$ 在ζ=0处有一个最大值1,且最大值随n的增加而逐渐减小。

基于上面的假设,通过(25)式,利用存在和不存在孤子时的巨正则能量差,可算出单位面积的孤子能量。不存在孤子时的体系能量是g $ρ_{0}^{n + 1}$ /(n+1)-μρ₀,所以存在和不存在孤子时的能量差为

E_{n} = \overset{+ \infty}{\int_{- \infty}} [\frac{ћ^{2}}{2 m} {|\frac{\partial ψ_{ans}}{\partial x}|}^{2} + \frac{g}{n + 1} (| ψ_{ans} |^{2 n + 2} - ρ_{0}^{n + 1}) - μ (| ψ_{ans} |^{2} - ρ_{0})] d x 。 (28)

注意到不存在孤子时的非线性相互作用为g $ρ_{0}^{n}$ 。

图3给出了不同n和v时的孤子能量。可以看出,在静态孤子状态,即v=0时,孤子能量随着n的增加而逐渐变大; 随着v的增加,孤子的能量逐渐减小,当孤子的运动速度趋近于声速时孤子的能量为零,孤子消失。因此,对于给定的非线性指数n,速度越小,孤子能量越大;当孤子速度增加时,n越大,能量下降也越快。这里考虑的是暗孤子,其密度曲线上有一个凹陷,研究表明,暗孤子在能量上不稳定,这个不稳定性对孤子的加速运动有贡献,但不会使孤子塌缩^[42-43]。

图 3. 不同速度下孤子能量随n的变化关系

Fig. 3. Variation of soliton energy with n for different speeds

下载图片查看所有图片

4 结论

分析了推广的具有2n+1次非线性的薛定谔方程的暗孤子激发态,从静态和动态两个方面分别研究了黑孤子和灰孤子的演化行为,给出了具有不同多方指数的静态孤子波函数的解析表达式。研究结果显示,对于静态暗孤子,随着多方指数的增加,孤子宽度越来越小但最低深度保持不变。分析了n和v对灰孤子动力学的影响,研究了孤子速度从零开始增加直至体系声速过程中的孤子演化。计算结果表明,借助一个含空间变量的因子,可以给出一个描述灰孤子波函数的统一表达式,此时波函数的虚部是一个常数。特别地,立方非线性薛定谔方程所给出的暗孤子解可以看成是具有2n+1次非线性的薛定谔方程的暗孤子解在n=1时的特殊情况。此外,在任意非线性相互作用强度下,当孤子速度趋近于声速时,孤子能量均趋于零。根据已有的物理结论,对非线性薛定谔方程进行了推广,研究了相应的暗孤子特性,以期为高次非线性相关问题的研究提供思路。

参考文献

[1] Liu WM, KengneE. Schrödinger equations in nonlinear systems[M]. Singapore: Springer, 2019.

[2] Kevrekidis PG, Frantzeskakis DJ, Carretero-GonzálezR. The defocusing nonlinear Schrödinger equation[M]. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2015.

[3] FibichG. The nonlinear Schrödinger equation: singular solutions and optical collapse[M]. New York: Springer, 2015.

[4] Chen ZJ. Solutions of nonlinear Schrödinger systems[M]. Heidelberg: Springer, 2015.

[5] SulemC, Sulem PL. The nonlinear Schrödinger equation: self-focusing and wave collapse[M]. New York: Springer, 2004.

[6] DauxoisT, PeyrardM. Physics of solitons[M]. Cambridge: Cambridge University Press, 2006.

[7] Williams MC. Solitons[M]. Hauppauge: Nova Science Publishers, 2013.

[8] Hu X H, Zhang X F, Zhao D, et al. Dynamics and modulation of ring dark solitons in two-dimensional Bose-Einstein condensates with tunable interaction[J]. Physical Review A, 2009, 79(2): 023619.

[9] Liang Z X, Zhang Z D, Liu W M. Dynamics of a bright soliton in Bose-Einstein condensates with time-dependent atomic scattering length in an expulsive parabolic potential[J]. Physical Review Letters, 2005, 94(5): 050402.

[10] Wu B, Liu J, Niu Q. Controlled generation of dark solitons with phase imprinting[J]. Physical Review Letters, 2002, 88(3): 034101.

[11] Huang G X, Makarov V A, Velarde M G. Two-dimensional solitons in Bose-Einstein condensates with a disk-shaped trap[J]. Physical Review A, 2003, 67(2): 023604.

[12] Triki H, Zhou Q, Liu W J. W-shaped solitons in inhomogeneous cigar-shaped Bose-Einstein condensates with repulsive interatomic interactions[J]. Laser Physics, 2019, 29(5): 055401.

[13] Brand J, Reinhardt W P. Solitonic vortices and the fundamental modes of the “snake instability”: possibility of observation in the gaseous Bose-Einstein condensate[J]. Physical Review A, 2002, 65(4): 043612.

[14] Donadello S, Serafini S, Tylutki M, et al. Observation of solitonic vortices in Bose-Einstein condensates[J]. Physical Review Letters, 2014, 113(6): 065302.

[15] Ku M J, Ji W J, Mukherjee B, et al. Motion of a solitonic vortex in the BEC-BCS crossover[J]. Physical Review Letters, 2014, 113(6): 065301.

[16] Sakaguchi H. New models for multi-dimensional stable vortex solitons[J]. Frontiers of Physics, 2019, 14: 12301.

[17] Anderson B P, Haljan P C, Regal C A, et al. Watching dark solitons decay into vortex rings in a Bose-Einstein condensate[J]. Physical Review Letters, 2001, 86(14): 2926-2929.

[18] Yang S J, Wu Q S, Zhang S N, et al. Generating ring dark solitons in an evolving Bose-Einstein condensate[J]. Physical Review A, 2007, 76(6): 063606.

[19] Becker C, Sengstock K, Schmelcher P, et al. Inelastic collisions of solitary waves in anisotropic Bose-Einstein condensates: sling-shot events and expanding collision bubbles[J]. New Journal of Physics, 2013, 15(11): 113028.

[20] Qi Y, Sun H, Niu Y, et al. Ultraslow solitons and soliton pairs in asymmetric quantum wells[J]. Chinese Journal of Lasers, 2009, 36(s1): 96-99.

[21] Dutta S, Mueller E J. Collective modes of a soliton train in a fermi superfluid[J]. Physical Review Letters, 2017, 118(26): 260402.

[22] Herink G, Kurtz F, Jalali B, et al. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules[J]. Science, 2017, 356(6333): 50-54.

[23] Spuntarelli A, Carr L D, Pieri P, et al. Gray solitons in a strongly interacting superfluid Fermi gas[J]. New Journal of Physics, 2011, 13(3): 035010.

[24] Reichl M D, Mueller E J. Core filling and snaking instability of dark solitons in spin-imbalanced superfluid Fermi gases[J]. Physical Review A, 2017, 95(5): 053637.

[25] Burger S, Bongs K, Dettmer S, et al. Dark solitons in Bose-Einstein condensates[J]. Physical Review Letters, 1999, 83(25): 5198-5201.

[26] Denschlag J, Simsarian J E, Feder D L, et al. Generating solitons by phase engineering of a Bose-Einstein condensate[J]. Science, 2000, 287(5450): 97-101.

[27] Khaykovich L, Schreck F, Ferrari G, et al. Formation of a matter-wave bright soliton[J]. Science, 2002, 296(5571): 1290-1293.

[28] Kevrekidis PG, Frantzeskakis DJ, Carretero-GonzálezR. Emergent nonlinear phenomena in Bose-Einstein condensates[M]. Heidelberg: Springer, 2008.

[29] Zhang X F, Hu X H, Liu X X, et al. Vector solitons in two-component Bose-Einstein condensates with tunable interactions and harmonic potential[J]. Physical Review A, 2009, 79(3): 033630.

[30] Liu X X, Pu H, Xiong B, et al. Formation and transformation of vector solitons in two-species Bose-Einstein condensates with a tunable interaction[J]. Physical Review A, 2009, 79(1): 013423.

[31] 赵岩, 宋丽军, 王艳. 多组分耦合非线性薛定谔方程的3-孤子解及其相互作用[J]. 光学学报, 2019, 39(4): 0419001.

Zhao Y, Song L J, Wang Y. 3-soliton solutions of multi-component coupled nonlinear Schrödinger equation and their interaction[J]. Acta Optica Sinica, 2019, 39(4): 0419001.

[32] Köhler T. Three-body problem in a dilute Bose-Einstein condensate[J]. Physical Review Letters, 2002, 89(21): 210404.

[33] Huang T W, Zhou C T, He X T. Propagation of femtosecond terawatt laser pulses in N2 gas including higher-order Kerr effects[J]. AIP Advances, 2012, 2(4): 042190.

[34] Kolomeisky E B, Newman T J, Straley J P, et al. Low-dimensional Bose liquids: beyond the Gross-Pitaevskii approximation[J]. Physical Review Letters, 2000, 85(6): 1146-1149.

[35] Zhan C L, Zhang D Q, Zhu D B, et al. Third- and fifth-order optical nonlinearities in a new stilbazolium derivative[J]. Journal of the Optical Society of America B, 2002, 19(3): 369-375.

[36] 杜英杰, 杨战营, 谢小涛, 等. 电磁感应透明的高阶非线性效应对光孤子的影响[J]. 光学学报, 2015, 35(2): 0227002.

Du Y J, Yang Z Y, Xie X T, et al. Influence of higher nonlinearity to optical solitons in electromagnetically induced transparency medium[J]. Acta Optica Sinica, 2015, 35(2): 0227002.

[37] Vakhitov N G, Kolokolov A A. Stationary solutions of the wave equation in a medium with nonlinearity saturation[J]. Radiophysics and Quantum Electronics, 1973, 16(7): 783-789.

[38] Weinstein M I. Lyapunov stability of ground states of nonlinear dispersive evolution equations[J]. Communications on Pure and Applied Mathematics, 1986, 39(1): 51-67.

[39] ViolaC. An introduction to special functions[M]. Cham: Springer, 2016.

[40] Seaborn JB. Hypergeometric functions and their applications[M]. New York: Springer, 1991.

[41] Antezza M, Dalfovo F, Pitaevskii L P, et al. Dark solitons in a superfluid Fermi gas[J]. Physical Review A, 2007, 76(4): 043610.

[42] Pethick CJ, SmithH. Bose-Einstein condensation in dilute gases[M]. 2nd ed. Cambridge: Cambridge University Press, 2008.

[43] PitaevskiiL, StringariS. Bose-Einstein condensation and superfluidity[M]. Oxford: Oxford University Press, 2016.

周昱, 张远, 王颖, 赵明琳, 闫东广. 具有2n+1次非线性的薛定谔方程暗孤子特性[J]. 光学学报, 2020, 40(9): 0927001. Yu Zhou, Yuan Zhang, Ying Wang, Minglin Zhao, Donguang Yan. Dark Soliton Properties of Nonlinear Schrödinger Equation with (2n+1)-th Order Nonlinearity[J]. Acta Optica Sinica, 2020, 40(9): 0927001.

具有2n+1次非线性的薛定谔方程暗孤子特性下载： 934次

1 引言

2 非线性薛定谔方程和静态暗孤子

图 1. 静态暗孤子的波函数和粒子数密度在不同n下随x的变化。(a)波函数,插图是孤子波函数的局部放大;(b)粒子数密度

Fig. 1. Evolution of wave function and particle number density of static dark soliton with x for different n. (a) Wave function with its local magnification shown in inset; (b) particle number density

3 运动暗孤子

图 2. v=0.8s时灰孤子的粒子数密度和相位在不同n下随ζ的变化。(a)粒子数密度;(b)相位

Fig. 2. Variation of particle number density and phase of gray soliton with ζ for different n at v=0.8s. (a) Particle number density; (b) phase

图 3. 不同速度下孤子能量随n的变化关系

Fig. 3. Variation of soliton energy with n for different speeds

4 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

具有2n+1次非线性的薛定谔方程暗孤子特性 下载： 934次

1 引言

2 非线性薛定谔方程和静态暗孤子

图 1. 静态暗孤子的波函数和粒子数密度在不同n下随x的变化。(a)波函数,插图是孤子波函数的局部放大;(b)粒子数密度

Fig. 1. Evolution of wave function and particle number density of static dark soliton with x for different n. (a) Wave function with its local magnification shown in inset; (b) particle number density

3 运动暗孤子

图 2. v=0.8s时灰孤子的粒子数密度和相位在不同n下随ζ的变化。(a)粒子数密度;(b)相位

Fig. 2. Variation of particle number density and phase of gray soliton with ζ for different n at v=0.8s. (a) Particle number density; (b) phase

图 3. 不同速度下孤子能量随n的变化关系

Fig. 3. Variation of soliton energy with n for different speeds

4 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

具有2n+1次非线性的薛定谔方程暗孤子特性下载： 934次