Bosonic discrete supersymmetry for quasi-two-dimensional optical arrays

Q. Zhong; S. Nelson; M. Khajavikhan; D. N. Christodoulides; R. El-Ganainy

doi:doi:10.1364/PRJ.7.001240

Photonics Research, 2019, 7 (11): 11001240, Published Online: Oct. 22, 2019

Bosonic discrete supersymmetry for quasi-two-dimensional optical arrays

论文大纲

Q. Zhong ^1,2S. Nelson ^1,2M. Khajavikhan ³D. N. Christodoulides ³R. El-Ganainy ^1,2,*

Author Affiliations

¹ Department of Physics, Michigan Technological University, Houghton, Michigan 49931, USA

² Henes Center for Quantum Phenomena, Michigan Technological University, Houghton, Michigan 49931, USA

³ College of Optics & Photonics-CREOL, University of Central Florida, Orlando, Florida 32816, USA

Abstract

We apply the notion of discrete supersymmetry based on matrix factorization to quantum systems consisting of coupled bosonic oscillators to construct isospectral bosonic quantum networks. By using the algebra that arises due to the indistinguishability of bosonic particles, we write down the Schr dinger equations for these oscillators in the different boson-number sectors. By doing so, we obtain, for every partner quantum network, a system of coupled differential equations that can be emulated by classical light propagation in optical waveguide arrays. This mathematical scheme allows us to build quasi-two-dimensional optical arrays that are either isospectral or share only a subset of their spectrum after deliberately omitting some chosen eigenstates from the spectrum. As an example, we use this technique (which we call bosonic discrete supersymmetry or BD-SUSY) to design two optical, silica-based waveguide arrays consisting of six and three elements, respectively, with overlapping eigenspectrum.

1. INTRODUCTION

Supersymmetry (SUSY) was first proposed in the context of high energy physics to relate fermionic and bosonic particles ^{[13" target="_self" style="display: inline;">–3]}. Later, SUSY was introduced in quantum mechanics ^{[46" target="_self" style="display: inline;">–6]}. By using the mathematical analogy between the single particle Schrödinger and the electromagnetic wave equation, the SUSY notion was recently extended to the field of photonics ^[7,8] with possible applications in optical communications ^[9], building new metamaterials ^[10], optical circuits ^[11], Bragg gratings ^[12], and mode selection ^[13], to mention a few examples. From a technological perspective, implementing continuous supersymmetry requires precise control of the refractive index profile at a subwavelength scale. Additionally, it may also require refractive index values beyond those obtained by current photonic material systems. To overcome these difficulties, a discrete version of SUSY (D-SUSY) that relies on matrix factorization schemes can be used ^[9,14]. In this case, a waveguide (or resonator) array described by a matrix Hamiltonian obtained by using coupled mode formalism can be used to construct a supersymmetric partner array that exhibits the same spectrum or a chosen subset of it ^[9,14]. The advantage of D-SUSY is that the supersymmetric partner array can be implemented by using the standard photonic materials. The tuning parameters here are the width/height of the waveguides as well as their separations, which can be well-controlled during the fabrication processes. This technique, together with non-Hermitian engineering, was recently used to propose ^[15,16] and later demonstrate ^[17] a universal solution for a long-standing problem in laser engineering, namely to build on-chip phase-locked laser arrays ^[17,18]. In most of these works, however, the D-SUSY construction was one-dimensional. The reason is that the various factorization techniques (i.e. Cholesky or QR ^[19]) preserve the structure of the original matrix only if it is tridiagonal. Within the next-neighbor approximation, tridiagonal matrices describe one-dimensional arrays. On the other hand, if the array is two-dimensional, then it is described by a more complex matrix structure. In this case, matrix factorization techniques introduce new long-range couplings which are not easy to implement using planar photonic technology. To alleviate some of these difficulties, recent works proposed a different route to D-SUSY based on Householder algorithm ^[16,20], which in effect reduces the array dimensionality.

Here we introduce a new approach towards building two-dimensional supersymmetric photonic structures. Essentially, we apply the notion of D-SUSY not directly to the classical array but to a quantum version made of one-dimensional coupled bosonic oscillators. By applying D-SUSY to this quantum array, we obtain a supersymmetric quantum array that shares the same eigenvalues but different eigenvectors. By properly shifting the eigenvalues of the original array, one can also eliminate some chosen eigenvalues from the SUSY array. The next step is to use the Schrödinger equation in order to expand the associated Hamiltonians in the relevant boson-number sectors. By doing so, we obtain a system of coupled differential equations for every partner quantum network. These classical equations can be emulated by light propagation in optical waveguide arrays ^[21,22]. Interestingly, when an $M$ -boson sector is considered in a quantum array having more than two oscillators, then the resultant optical arrays are two-dimensional for $M > 1$ . This powerful mathematical tool (which we call bosonic discrete SUSY, or BD-SUSY for short) thus opens the door for engineering a wide range of two-dimensional geometries with well-specified spectral relations — a task that is not possible using conventional D-SUSY method.

2. RESULTS AND DISCUSSION

In order to demonstrate the power of this new technique, we consider a system of one-dimensional three coupled bosonic oscillators (extension to larger systems is mathematically straightforward; though, it can lead to challenges in implementations): where $β_{o}$ (we use this symbol in anticipation of the implementation using waveguide arrays where $β_{o}$ will play the role of the propagation constant of isolated channels) and $κ$ are the on-site energy and next neighbor coupling, respectively, and H.c. denotes the Hermitian conjugate. Equivalently, the system in Eq. (1) can be expressed using the Heisenberg equation of motions for the operators ${\hat{a}}_{n}$ , $i d {\hat{a}}_{n} / d z = - \frac{1}{ℏ} [\hat{H}, {\hat{a}}_{n}]$ (again, we used the distance $z$ instead of time $t$ to relate these equations directly to waveguide structures ^[21,22]): where $\vec{\hat{a}} = {({\hat{a}}_{1}, {\hat{a}}_{2}, {\hat{a}}_{3})}^{T}$ . We can now perform D-SUSY mapping on the matrix $M$ as follows: where $Q$ and $R$ are the matrices obtained from the $Q R$ decomposition, $I$ is a unitary matrix, and $β_{S}$ is a constant. It is easy to verify that the matrices $H$ and $H^{S}$ are isospectral. Importantly, the matrix $H^{S}$ is tridiagonal and symmetric. Consequently, one can construct a one-dimensional quantum network that is isospectral with that of $\hat{H}$ via the Hamiltonian: In other words, the diagonal forms of both $\hat{H}$ and ${\hat{H}}^{S}$ are given by where $(λ_{n} - β_{o}) \in {0, \pm \sqrt{2} κ}$ are the eigenvalues of the matrix $H$ and also $H^{S}$ . The operators $\hat{A}$ and $\hat{B}$ are related to $\hat{a}$ by linear transformations defined by the eigenvectors of the matrices $H$ and $H^{S}$ , respectively.

Let us now assume that the bosonic networks described by $\hat{H}$ are populated by $M$ bosons. They can be distributed according to $| m_{1}, m_{2}, m_{3} ⟩$ (indicating $m_{n}$ bosons in site $n$ ) where $M = m_{1} + m_{2} + m_{3}$ . These states can be arranged in any order and expressed in terms of one index, say $m = 1, 2, \dots, w$ , where $w = \frac{1}{2} (M + 2) (M + 1)$ ^[23]. The general wavefunction can be thus written as $| ψ ⟩ = \sum_{m = 1}^{w} c_{m} | m ⟩$ . Similarly, for ${\hat{H}}^{S}$ , we obtain $| ψ^{S} ⟩ = \sum_{m = 1}^{w} c_{m}^{S} | m^{S} ⟩$ . By substituting $\hat{H}$ and ${\hat{H}}^{S}$ back in and projecting on the states $| m ⟩$ and $| m^{S} ⟩$ , respectively, we obtain two different sets of coupled ordinary differential equations (ODEs): one for the coefficients $c_{m}$ and another for $c_{m}^{S}$ . Each of these coupled ODEs can be emulated by a classical waveguide array.

Particularly, for concreteness, we will consider an example with $M = 2$ . Additionally, we will use this example to illustrate how one can build a partner network after eliminating some of the eigenvalues. To do so, we make the choice $β_{s} = β_{o}$ . As a result, we find that We can thus consider only the $2 \times 2$ block diagonal, which is equivalent to omitting the state with eigenvalue $β_{o}$ : The subscript $R$ indicates that this is a reduced Hamiltonian, which has the diagonal form: here $(μ_{n} - β_{0}) \in {\pm \sqrt{2} κ}$ . Figure 1 shows the corresponding classical networks of these quantum oscillators when populated with two bosons. In this case, the main and partner arrays have eigenvalues that correspond to their optical super modes given by $(β_{m} - β_{o}) \in {0, \pm \sqrt{2} κ, \pm 2 \sqrt{2} κ}$ and $(β_{m}^{S} - β_{o}) \in {0, \pm 2 \sqrt{2} κ}$ , respectively. In other words, the partner array shares all the eigenvalues of the main array except $\pm \sqrt{2} κ$ . Importantly, by inspecting Eq. (7), we note that the waveguides in the main and partner arrays are identical, which simplify the implementation significantly.

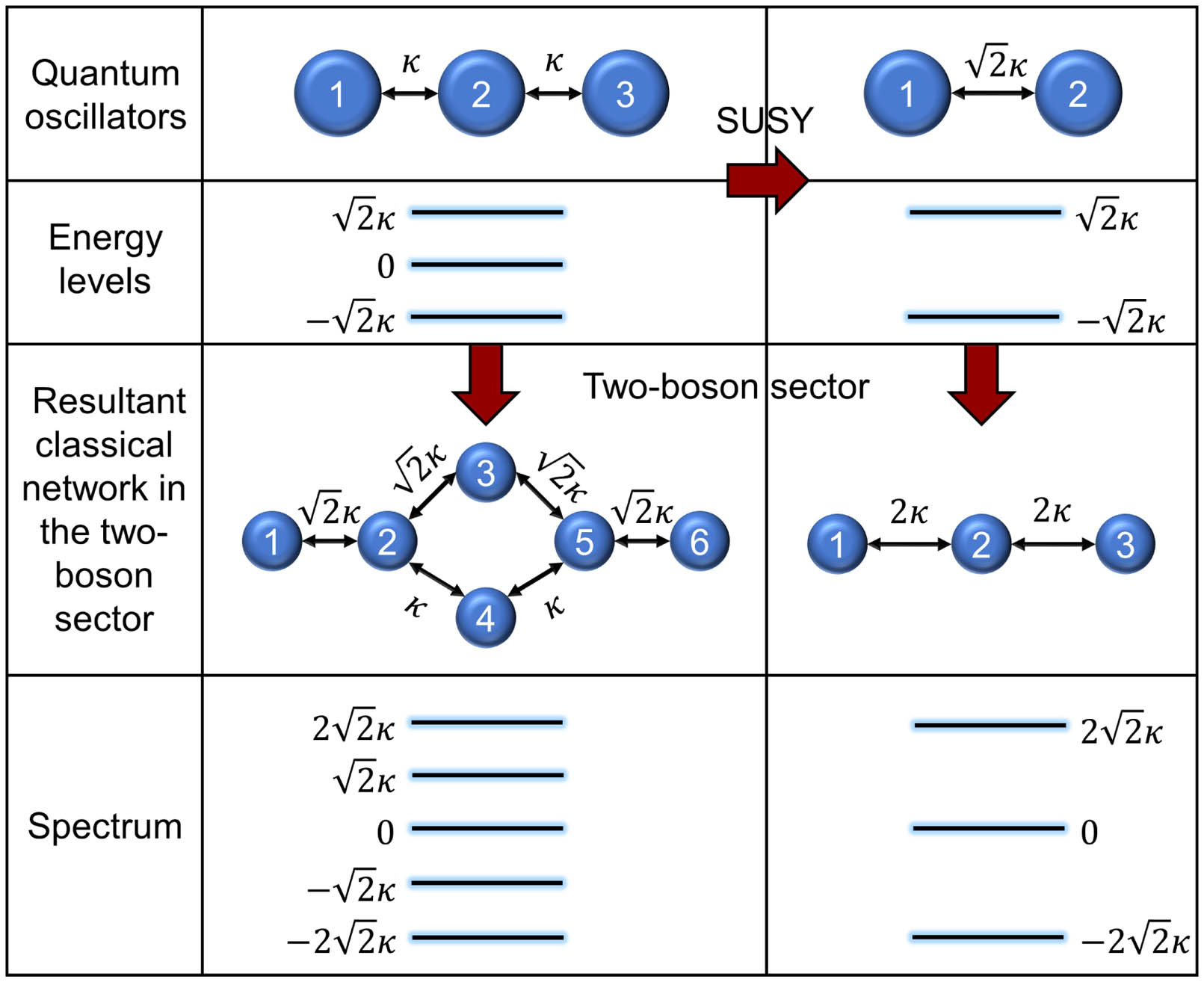
Summary of our proposed approach. A discrete SUSY transformation is applied to a set of N coupled quantum oscillators (for demonstration, we take N=3). The resultant partner network made of N−1 elements exhibits a subset of the spectrum of the original system. By populating both quantum networks with multiple bosons (2 bosons in the example shown here), we can construct classical arrays that exhibit partial spectral overlap.

Fig. 1. Summary of our proposed approach. A discrete SUSY transformation is applied to a set of $N$ coupled quantum oscillators (for demonstration, we take $N = 3$ ). The resultant partner network made of $N - 1$ elements exhibits a subset of the spectrum of the original system. By populating both quantum networks with multiple bosons (2 bosons in the example shown here), we can construct classical arrays that exhibit partial spectral overlap.

下载图片查看所有图片

Figure 2 plots a realistic implementation of these networks in silica-glass-based waveguide systems. The design parameters along with the resultant coupling coefficients are all listed in the figure caption.

$Optical implementation of the SUSY arrays example shown in Fig. 1 using a waveguide platform. The left panel shows the original array while right panel shows the BD-SUSY partner obtained as described in the text. The waveguides are all identical, having an elliptic geometry with main/minor diameters of 12 and 6 μm, respectively. The core and cladding refractive indices are taken to be ncore=1.461 and nclad=1.46, respectively [24,25]. Each waveguide supports only one optical mode for each polarization direction. Finally, the distances shown in panel (a) are: d1=23.765 μm, d2=18.275 μm, and d3=16.190 μm. These design parameters result in the following coupling coefficients: κ12=14.143 m−1, κ23=13.141 m−1, and κ24=10.000 m−1. The second order nearest next neighbor coupling is found to be below 10% of the above values. Similarly, in panel (b) we have: d4=22.425 μm and κ12=20.012 m−1. Note that we list the above values with high precision as per our numerical simulations; however, in practice the weakly guiding nature of the structure provides reasonable robustness against fabrication tolerance.$

Fig. 2. Optical implementation of the SUSY arrays example shown in Fig. 1 using a waveguide platform. The left panel shows the original array while right panel shows the BD-SUSY partner obtained as described in the text. The waveguides are all identical, having an elliptic geometry with main/minor diameters of 12 and 6 μm, respectively. The core and cladding refractive indices are taken to be $n_{core} = 1.461$ and $n_{clad} = 1.46$ , respectively [24,25]. Each waveguide supports only one optical mode for each polarization direction. Finally, the distances shown in panel (a) are: $d_{1} = 23.765 μm$ , $d_{2} = 18.275 μm$ , and $d_{3} = 16.190 μm$ . These design parameters result in the following coupling coefficients: $κ_{12} = 14.143 m^{- 1}$ , $κ_{23} = 13.141 m^{- 1}$ , and $κ_{24} = 10.000 m^{- 1}$ . The second order nearest next neighbor coupling is found to be below 10% of the above values. Similarly, in panel (b) we have: $d_{4} = 22.425 μm$ and $κ_{12} = 20.012 m^{- 1}$ . Note that we list the above values with high precision as per our numerical simulations; however, in practice the weakly guiding nature of the structure provides reasonable robustness against fabrication tolerance.

下载图片查看所有图片

Figure 3 depicts the eigenmodes and eigenvalues associated with the photonic networks in Fig. 2 as obtained by full-wave finite element simulations. These results clearly illustrate the partial spectral overlap as predicted exactly by the discrete model.

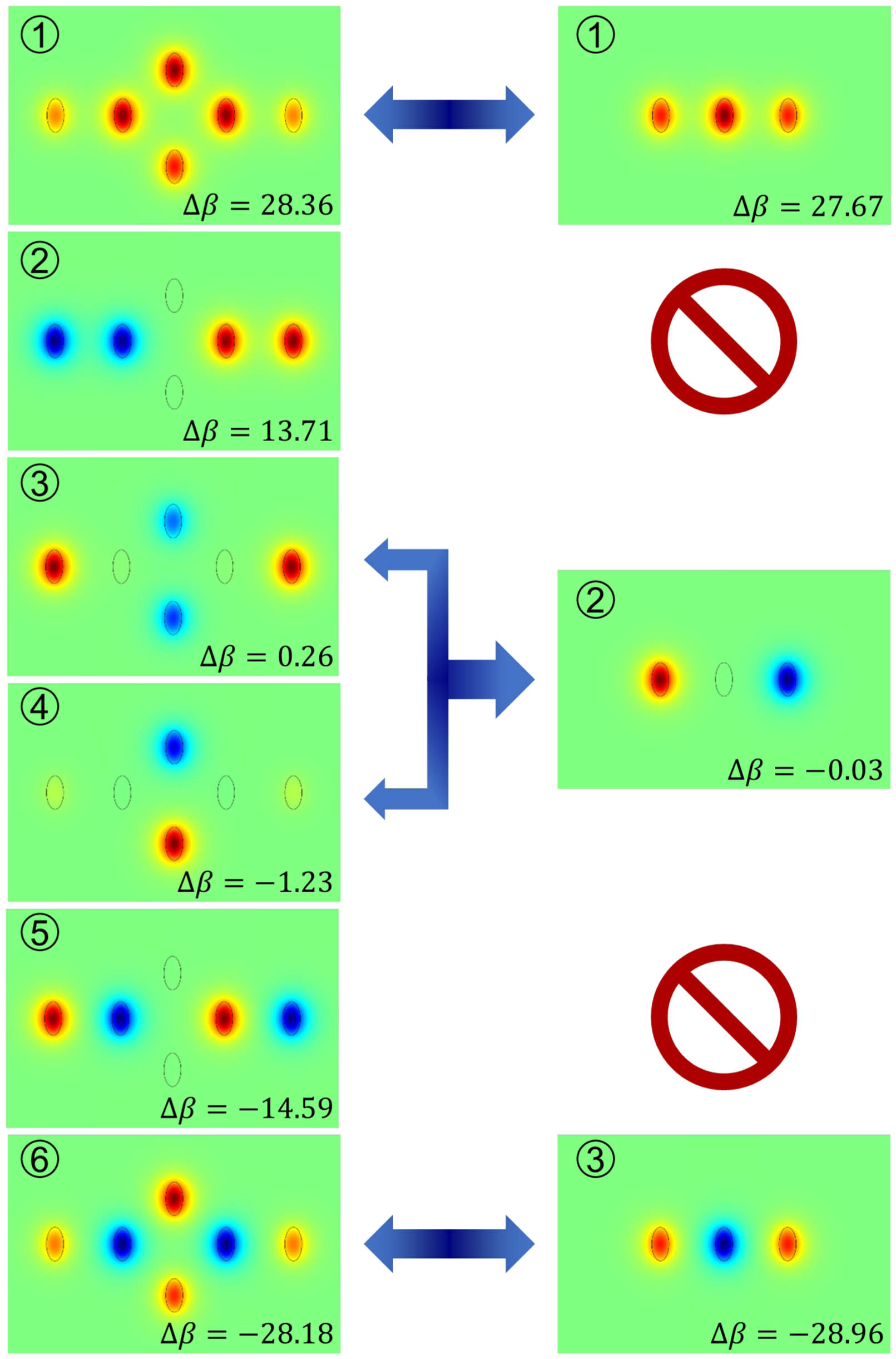
Eigenmode structure of the waveguide arrays shown in Figs. 2(a) and 2(b) are depicted in the left and right panels, respectively (obtained by full-wave finite element simulations). The figures also indicate the values of the associated propagation constants as measured from the isolated waveguide value, i.e., Δβ=βm−βo (in units of m−1), where βm,o are the propagation constants of array mode m and the isolated waveguide mode, correspondingly. As anticipated from the coupled mode analysis, modes ② and ⑤ in the main array have no partner modes in the BD-SUSY partner array. Moreover, mode ② of the partner array corresponds to two degenerate states in the main array. These results confirm the feasibility of our approach for building quasi-2D supersymmetric optical systems.

Fig. 3. Eigenmode structure of the waveguide arrays shown in Figs. 2(a) and 2(b) are depicted in the left and right panels, respectively (obtained by full-wave finite element simulations). The figures also indicate the values of the associated propagation constants as measured from the isolated waveguide value, i.e., $Δ β = β_{m} - β_{o}$ (in units of $m^{- 1}$ ), where $β_{m, o}$ are the propagation constants of array mode $m$ and the isolated waveguide mode, correspondingly. As anticipated from the coupled mode analysis, modes ② and ⑤ in the main array have no partner modes in the BD-SUSY partner array. Moreover, mode ② of the partner array corresponds to two degenerate states in the main array. These results confirm the feasibility of our approach for building quasi-2D supersymmetric optical systems.

下载图片查看所有图片

Finally, we also study the evolutionary dynamics of light in these waveguide arrays when a small coupling ( $κ = 1 m^{- 1}$ ) is introduced between the rightmost waveguide of the main array and the leftmost channel of the partner array. Figures 4(a)–4(e) plot the optical intensity profiles at different propagation cross sections when only mode ① of the main array is excited (i.e., there is zero input in the partner array). Clearly, at a distance that corresponds to a full period (which in the current design corresponds to $z = 4 π$ in units of meter), the total power is transferred to mode ① of the partner array with an efficiency $\sim 100 %$ as can be seen from Fig. 4(f). On the other hand, when mode ② of the main array is excited, we observe almost no power transfer to the partner array, as expected to due to the phase mismatch (see Fig. 3). Importantly, we note that similar designs with scaled parameters can be implemented using shorter structures ^[26] or even in resonators where propagation distance is replaced by time.

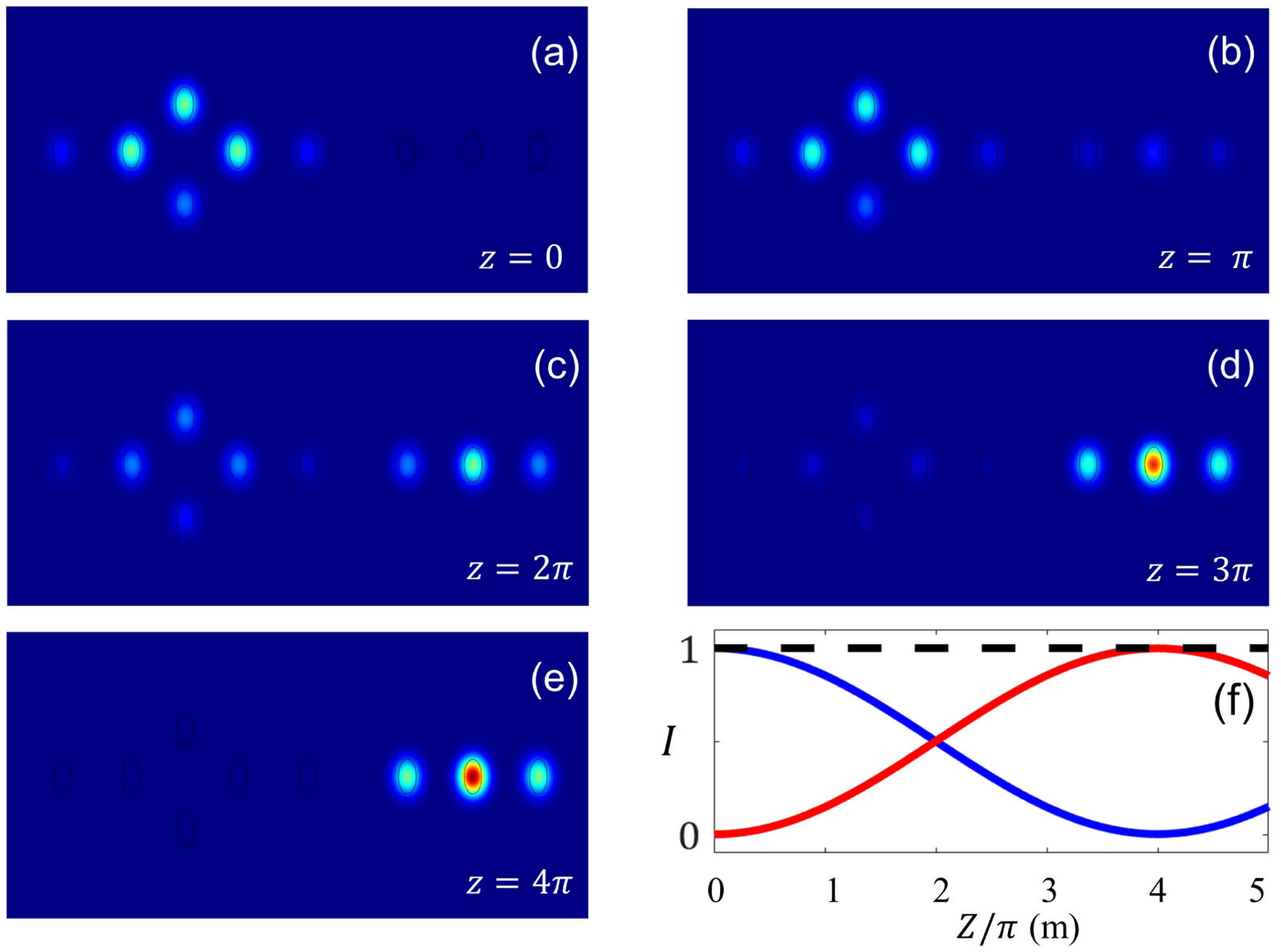
Light propagation dynamics in a waveguide array formed by introducing a weak coupling between the main structure and its partner, as shown in (a)–(e). When mode ① of the main array is excited, we observe an efficient optical power transfer to the partner array after a propagation distance corresponding to z=4π (in units of meter). On the other hand, if mode ② of the main array is excited, no appreciable power transfer to the partner array is observed (not shown here). The power transfer efficiency between the modes is illustrated in (f) where near perfect transfer is observed. The blue and red lines are the total power in the main and pattern arrays, respectively.

Fig. 4. Light propagation dynamics in a waveguide array formed by introducing a weak coupling between the main structure and its partner, as shown in (a)–(e). When mode ① of the main array is excited, we observe an efficient optical power transfer to the partner array after a propagation distance corresponding to $z = 4 π$ (in units of meter). On the other hand, if mode ② of the main array is excited, no appreciable power transfer to the partner array is observed (not shown here). The power transfer efficiency between the modes is illustrated in (f) where near perfect transfer is observed. The blue and red lines are the total power in the main and pattern arrays, respectively.

下载图片查看所有图片

3. CONCLUSIONS

In conclusion, to the best of our knowledge, we have introduced a new approach for engineering two-dimensional optical arrays that exhibit complete or partial spectral overlap. Our method relies on the bosonic algebra of coupled quantum oscillators, essentially applying the D-SUSY to the corresponding Heisenberg equation of motions followed by expanding the relevant Hamiltonians in their Fock space. The resultant ODEs can be then emulated by classical waveguide arrays. When considering a certain boson sector that has more than one photon, this technique gives rise to optical arrays that have two-dimensional connectivities (i.e., are not represented by tridiagonal matrices). We have demonstrated our technique by designing two different arrays having six and three waveguides, with the spectrum of the latter being a subset of that of the former. We have also presented an implementation for these structures based on waveguide arrays in glass platforms. Our full-wave simulations using the finite element method and coupled mode theory confirm our theoretical predictions. Finally, we emphasize that our technique can in principle be applied to any 1D network structure in order to obtain a quasi 2D SUSY partner. However, implementing more complex arrangements using optical platforms maybe challenging, mainly due to the geometric restrictions imposed by the waveguides (or resonators). In this regard, a platform that can be of potential interest is superconducting circuits which was shown recently to provide more degrees of freedom for implementing hyperbolic lattices ^[27]. We will investigate how D-SUSY can benefit from this promising platform in future work.

References

[1] P. Ramond. Dual theory for free fermions. Phys. Rev. D, 1971, 3: 2415-2418.

[2] A. Neveu, J. H. Schwarz. Factorizable dual model of pions. Nucl. Phys. B, 1971, 31: 86-112.

[3] E. Witten. Dynamical breaking of supersymmetry. Nucl. Phys. B, 1981, 188: 513-554.

[4] F. Cooper, B. Freedman. Aspects of supersymmetric quantum mechanics. Ann. Phys., 1983, 146: 262-288.

[5] A. Lahiri, P. K. Roy, B. Bagchi. Supersymmetry in quantum mechanics. Int. J. Mod. Phys. A, 1990, 05: 1383-1456.

[6] F. Cooper, A. Khare, U. Sukhatme. Supersymmetry and quantum mechanics. Phys. Rep., 1995, 251: 267-385.

[7] R. El-Ganainy, K. G. Makris, D. N. Christodoulides. Local PT invariance and supersymmetric parametric oscillators. Phys. Rev. A, 2012, 86: 033813.

[8] M.-A. Miri, M. Heinrich, R. El-Ganainy, D. N. Christodoulides. Supersymmetric optical structures. Phys. Rev. Lett., 2013, 110: 233902.

[9] M. Heinrich, M.-A. Miri, S. Stützer, R. El-Ganainy, S. Nolte, A. Szameit, D. N. Christodoulides. Supersymmetric mode converters. Nat. Commun., 2014, 5: 3698.

[10] M.-A. Miri, M. Heinrich, D. N. Christodoulides. SUSY-inspired one-dimensional transformation optics. Optica, 2014, 1: 89-95.

[11] S. Longhi. Supersymmetric transparent optical intersections. Opt. Lett., 2015, 40: 463-466.

[12] S. Longhi. Supersymmetric Bragg gratings. J. Opt., 2015, 17: 045803.

[13] W. Walasik, B. Midya, L. Feng, N. M. Litchinitser. Supersymmetry-guided method for mode selection and optimization in coupled systems. Opt. Lett., 2018, 43: 3758-3761.

[14] M. Heinrich, M.-A. Miri, S. Stützer, S. Nolte, D. N. Christodoulides, A. Szameit. Observation of supersymmetric scattering in photonic lattices. Opt. Lett., 2014, 39: 6130-6133.

[15] R. El-Ganainy, L. Ge, M. Khajavikhan, D. N. Christodoulides. Supersymmetric laser arrays. Phys. Rev. A, 2015, 92: 033818.

[16] M. H. Teimourpour, L. Ge, D. N. Christodoulides, R. El-Ganainy. Non-Hermitian engineering of single mode two dimensional laser arrays. Sci. Rep., 2016, 6: 33253.

[17] M. P. Hokmabadi, N. S. Nye, R. El-Ganainy, D. N. Christodoulides, M. Khajavikhan. Supersymmetric laser arrays. Science, 2019, 363: 623-626.

[18] B. Midya, H. Zhao, X. Qiao, P. Miao, W. Walasik, Z. Zhang, N. M. Litchinitser, L. Feng. Supersymmetric microring laser arrays. Photon. Res., 2019, 7: 363-367.

[19] StrangG., Introduction to Linear Algebra, 5th ed. (Wellesley-Cambridge, 2016).

[20] S. Yu, X. Piao, J. Hong, N. Park. Interdimensional optical isospectrality inspired by graph networks. Optica, 2016, 3: 836-839.

[21] M. H. Teimourpour, R. El-Ganainy, A. Eisfeld, A. Szameit, D. N. Christodoulides. Light transport in PT-invariant photonic structures with hidden symmetries. Phys. Rev. A, 2014, 90: 053817.

[22] TeimourpourM. H.ZhongQ.KhajavikhanM.El-GanainyR., Higher Order Exceptional Points in Discrete Photonics Platforms (Springer, 2018), pp. 261–275.

[23] SchieveW. C.HorwitzL. P., Quantum Statistical Mechanics (Cambridge University, 2009).

[24] L. Shah, A. Y. Arai, S. M. Eaton, P. R. Herman. Waveguide writing in fused silica with a femtosecond fiber laser at 522 nm and 1 MHz repetition rate. Opt. Express, 2005, 13: 1999-2006.

[25] A. Szameit, J. Burghoff, T. Pertsch, S. Nolte, A. Tünnermann, F. Lederer. Two-dimensional soliton in cubic fs laser written waveguide arrays in fused silica. Opt. Express, 2006, 14: 6055-6062.

[26] T. Meany, M. Gräfe, R. Heilmann, A. Perez-Leija, S. Gross, M. J. Steel, M. J. Withford, A. Szameit. Laser written circuits for quantum photonics. Laser Photon. Rev., 2015, 9: 363-384.

[27] A. J. Kollár, M. Fitzpatrick, A. A. Houck. Hyperbolic lattices in circuit quantum electrodynamics. Nature, 2019, 571: 45-50.

1. INTRODUCTION

2. RESULTS AND DISCUSSION

3. CONCLUSIONS

Q. Zhong, S. Nelson, M. Khajavikhan, D. N. Christodoulides, R. El-Ganainy. Bosonic discrete supersymmetry for quasi-two-dimensional optical arrays[J]. Photonics Research, 2019, 7(11): 11001240.

Bosonic discrete supersymmetry for quasi-two-dimensional optical arrays

1. INTRODUCTION

2. RESULTS AND DISCUSSION

3. CONCLUSIONS

Article Outline

关于本站 Cookie 的使用提示

全站搜索

Bosonic discrete supersymmetry for quasi-two-dimensional optical arrays

1. INTRODUCTION

2. RESULTS AND DISCUSSION

3. CONCLUSIONS

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索