旋光效应对Bi<sub>12</sub>SiO<sub>20</sub>晶体中光动量及角动量的影响

陈舒婷; 郭昊旭; 邱晓东; 陈理想

doi:doi:10.3788/LOP56.132601

激光与光电子学进展, 2019, 56 (13): 132601, 网络出版: 2019-07-11

旋光效应对Bi₁₂SiO₂₀晶体中光动量及角动量的影响下载： 1002次

Influence of Optical Activity on Optical Momentum and Angular Momentum in Bi₁₂SiO₂₀ Crystals

论文大纲

陈舒婷郭昊旭邱晓东陈理想 ^*

作者单位

厦门大学物理科学与技术学院, 福建厦门 361005

物理光学晶体光学旋光效应光动量角动量 physical optics crystal optics optical activity optical momentum angular momentum

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

从Maxwell方程组出发,将与旋光效应相关的二阶非线性电极化作为线性电极化的微扰项,并结合角谱表示理论,以傍轴高斯光束作为入射光场,研究了光束在具有自然旋光性的Bi₁₂SiO₂₀晶体中的传播问题,并分别采用Minkowski和Abraham两种形式的光动量,得出Bi₁₂SiO₂₀晶体中的光动量及角动量表达式。结果表明,旋光性的存在使得晶体中的Minkowski动量和Abraham动量的比值不再是晶体折射率的平方。采用Minkowski角动量密度形式,可以发现,光场与晶体之间的角动量会发生耦合,虽然光场自身的角动量不守恒,但光场和晶体的总角动量守恒。

Abstract

Beginning from Maxwell's equations and by considering the second-order nonlinear polarization related to the optical activity as the perturbation of linear polarization, we investigate the propagation behavior of the paraxial Gaussian light which acts as incident light in the optically active medium Bi12SiO20 and utilize the Minkowski and Abraham momenta to obtain the expressions of optical momentum and angular momentum in Bi12SiO20 crystals. Further, we obtain that the ratio of Minkowski momentum to Abraham momentum is not equal to the square of the refractive index of the crystal because of the existence of optical activity. In the Minkowski picture, because of the coupling of the angular momentum between the light and the crystal, the angular momentum of the light field is not conserved, whereas the total angular momentum of the light and crystal is conserved.

1 引言

介质中光动量的正确形式持续争议了一个多世纪,争议起源于Minkowski^[1]和Abraham^[2]。多数理论研究表明,Abraham动量为介质中光子自身的动量,对应于物质的动力学动量,而Minkowski动量对应于物质的正则动量^[3-5]。对于各向同性透明介质,Minkowski动量与介质折射率成正比,而Abraham动量与介质折射率成反比。近年来,光动量问题被拓展到新的领域,人们开始研究电磁场在各向异性介质以及介电响应更复杂的介质中的能量、动量、角动量、辐射压力等问题。Antonoyiannakis等^[6]通过Maxwell应力张量的面积分来确定GaP小球组成的三维光子晶体中的光力,发现光对相邻GaP小球产生的是吸引力还是排斥力取决于光的频率。从经典Maxwell方程组出发,Mansuripur^[7]采用新形式的洛伦兹力研究介质中的光动量,提出光动量为Abraham和Minkowski动量之和的平均,并将其推广应用于分析色散介质^[8]、磁性介质^[9],以及具有亚波长结构介质中的光动量问题^[10]。在考虑色散和吸收的条件下,Kemp等^[11]研究了电磁场在相对介电常数ε_r和相对磁导率μ_r同时为负值的左手介质中的能量、动量、辐射压力,发现电磁场的动量密度和能流密度在无吸收的左手介质中方向相反,而在有吸收的左手介质中方向可能相同也可能相反,其方向取决于电磁场的频率。Feigel^[12]利用Blount和Nelson的经典场理论方法来研究量子真空对磁电介质的作用,预言了类似于Casimir力的现象。李东华等^[13]分析了透明介质平板在高斯光束照射下的受力情况,由动量守恒定理推导得出透明介质平板的受力表达式。此外,Ciattoni等^[14-15]采用角谱表示方法研究了光在单轴晶体中传播时的角动量特性,将晶体中光的角动量分为自旋角动量和轨道角动量^[16]两部分,发现晶体中光场的自旋-轨道角动量会发生耦合,沿光轴方向上晶体与光场的角动量各自守恒。之后,Lu等^[17]将角谱表示方法推广应用于分析光在双轴晶体中的角动量特性,发现在双轴晶体中光的自旋-轨道角动量同样发生耦合,但不同于单轴晶体,双轴晶体和光场之间角动量发生传递,因此晶体中光场自身的角动量不守恒。

硅酸铋晶体Bi₁₂SiO₂₀(BSO)是一种各向同性的自然旋光晶体,线偏振光在其间传播时偏振面会发生旋转,该现象被称为旋光效应^[18],与电极化率的空间色散相关^[19]。已有文献采用不同理论分析了光在旋光晶体中的传播^[20-21],但目前为止还没有相关文献研究旋光效应对光动量、角动量的具体影响。本文从Maxwell方程组出发,结合平面波角谱表示方法^[14,16,22],采用三阶赝张量 $\begin{matrix} κ_{jkl}^{(2)} \end{matrix}$ 描述晶体的旋光效应^[21,23],分析了傍轴高斯光束在BSO晶体中的传播行为,并就旋光性对晶体中的光动量及角动量特性的影响进行了定量分析。

2 理论

2.1 傍轴高斯光束在BSO晶体中的光电场和光动量

从Maxwell方程组出发,可以推导得出光在介质中的传播方程为^[13,17,24]

\begin{matrix} \nabla^{2} E (r) - \nabla [\nabla \cdot E (r)] + k_{0}^{2} ε \cdot E (r) = - μ_{0} ω^{2} P^{(2)} (r), (1) \end{matrix}

式中:ε为相对介电张量;μ₀为真空中磁导率;ω为光的圆频率;k₀=2π/λ为真空中光波数,λ为真空中波长;E(r)为光电场矢量;P⁽²⁾(r)为二阶非线性电极化强度;r为介质空间中的位置矢量。本文只考虑与旋光性相关的非线性电极化强度^[19] $\begin{matrix} P_{j}^{(2)} \end{matrix}$ =2ε₀ $\begin{matrix} κ_{jkl}^{(2)} \end{matrix} \begin{matrix} \nabla_{l} \end{matrix}$ E_k,其中ε₀为真空中介电常数, $\begin{matrix} \nabla_{l} \end{matrix}$ 为梯度算符的l分量,E_k为光电场矢量的k分量。与旋光性相关的三阶赝张量^[19,23]为 $\begin{matrix} κ_{jkl}^{(2)} \end{matrix}$ =- $\begin{matrix} \frac{ε_{jkm} g_{ml}}{2 n_{0} k_{0}} \end{matrix}$ ,其中ε_jkm和g_ml分别为Levi-Civita张量元素和旋光张量元素^[25],n₀为旋光介质的折射率。各向同性的硅酸铋旋光晶体BSO的三阶赝张量κ⁽²⁾可以表示为

\begin{matrix} κ^{(2)} = [\begin{matrix} 0 & 0 & 0 & - \frac{g}{2 n_{0} k_{0}} & \frac{g}{2 n_{0} k_{0}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & - \frac{g}{2 n_{0} k_{0}} & \frac{g}{2 n_{0} k_{0}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{g}{2 n_{0} k_{0}} & \frac{g}{2 n_{0} k_{0}} \end{matrix}], (2) \end{matrix}

式中:g=g₁₁=g₂₂=g₃₃,g₁₁、g₂₂、g₃₃为硅酸铋旋光晶体的旋光张量g的三个对角元。考虑一束光沿着z轴传播,入射到BSO晶体中的情形。利用平面波角谱表示方法可以将光电场表示为傅里叶积分的形式^[17,22],即

\begin{matrix} E (r_{⊥}, z) = \int d^{2} k_{⊥} \exp (i k_{⊥} \cdot r_{⊥}) \tilde{E} (k_{⊥}, z), (3) \end{matrix}

式中:r_⊥为横向坐标矢量;k_⊥为横向波矢量; $\begin{matrix} \tilde{E} \end{matrix}$ (k_⊥,z)为平面波的角谱。

将(3)式代入到传播方程(1)式当中,忽略反向传播的光波影响,可以推导出

\begin{matrix} \tilde{E} (k_{⊥}, z) = (\begin{matrix} c_{1} \\ c_{3} \\ c_{5} \end{matrix}) \exp (λ_{1} z) + (\begin{matrix} c_{2} \\ c_{4} \\ c_{6} \end{matrix}) \exp (λ_{2} z), (4) \end{matrix}

式中:λ₁、λ₂分别代表BSO旋光晶体中两独立传播的光波的纵向传播常数;c₁~c₆为相应平面波分量的权重系数。

忽略与三阶赝张量元 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ 有关的高阶小量,结合傍轴近似可得λ_1,2=i $\begin{matrix} (\sqrt[]{α - k_{⊥}^{2}} \mp δ) \end{matrix}$ ,其中参数α= $\begin{matrix} k_{0}^{2} \end{matrix} \begin{matrix} n_{0}^{2} \end{matrix}$ ,δ= $\begin{matrix} k_{0}^{2} \end{matrix} \begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ ,k_⊥代表横向波矢量的大小(即横向波数)。(4)式中的c₁~c₆可以表示为

\begin{matrix} \begin{matrix} [\begin{matrix} c_{1} \\ c_{3} \end{matrix}] = P_{1} \cdot {\tilde{E}}_{⊥} (0), [\begin{matrix} c_{2} \\ c_{4} \end{matrix}] = P_{2} \cdot {\tilde{E}}_{⊥} (0), (5) \\ [\begin{matrix} c_{5} \\ c_{6} \end{matrix}] = \frac{i}{α - k_{⊥}^{2}} \cdot [\begin{matrix} (λ_{1} k_{x} - 2 δ k_{y}) c_{1} + (λ_{1} k_{y} + 2 δ k_{x}) c_{3} \\ (λ_{2} k_{x} - 2 δ k_{y}) c_{2} + (λ_{2} k_{y} + 2 δ k_{x}) c_{4} \end{matrix}], (6) \end{matrix} \end{matrix}

式中: $\begin{matrix} {\tilde{E}}_{⊥} \end{matrix}$ (0)为初始入射平面z=0处横向电矢量的二维傅里叶变换;P₁和P₂为联系c₁~c₄系数与 $\begin{matrix} {\tilde{E}}_{⊥} \end{matrix}$ (0)的矩阵;k_x为横向波矢量的x分量;k_y为横向波矢量的y分量。上述的P₁和P₂矩阵为

\begin{matrix} P_{1,2} = \frac{1}{2} [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] \pm \frac{i}{2 \sqrt[]{α (α - k_{⊥}^{2})}} [\begin{matrix} - k_{x} k_{y} & - (α - k_{x}^{2}) \\ α - k_{y}^{2} & k_{x} k_{y} \end{matrix}] 。 (7) \end{matrix}

以左旋圆偏振傍轴高斯光束为入射光,初始光电场为E_⊥(r_⊥,0)=E₀exp{-[r²/(2s)²]}e₊,其中E₀为高斯光束的初始电矢量振幅,s为光束的束腰半径,e₊=(1/ $\begin{matrix} \sqrt[]{2} \end{matrix}$ )(e_x-ie_y)表示光束的偏振态为左旋圆偏振,其中e_x为水平线偏振态的单位矢量,e_y为竖直线偏振态的单位矢量。对初始光电场作傅里叶变换,可得初始条件 $\begin{matrix} {\tilde{E}}_{⊥} \end{matrix}$ (0)=[E₀s²/(2π)]·exp[-( $\begin{matrix} k_{⊥}^{2} \end{matrix}$ s²/2)]e₊。在坐标表象中,横向坐标矢量为r_⊥=r_⊥(cosφe_x+sinφe_y),其中φ为横向坐标矢量r_⊥与x轴的夹角;在动量表象中,横向波矢为k_⊥=k_⊥(cosθe_x+sinθe_y)^[26],其中θ为横向波矢量k_⊥与x轴的夹角。进一步可推导得傍轴高斯光束在BSO旋光晶体中的光电场为

\begin{matrix} \begin{matrix} E_{+} (r, φ, z) = \frac{E_{0} s^{2}}{s^{(2)} (z)} \exp (i k_{0} n_{0} z) \cdot \exp (- iσ) \exp [- \frac{r^{2}}{2 s^{(2)} (z)}], (8) \\ E_{-} (r, φ, z) = - \frac{E_{0} s^{2}}{2 α} \exp (i k_{0} n_{0} z) (isinσ) \cdot \frac{r^{2}}{{[s^{(2)} (z)]}^{3}} \exp [- \frac{r^{2}}{2 s^{(2)} (z)}] \exp (i 2 φ), (9) \\ E_{z} (r, φ, z) = - i \frac{E_{0} s^{2}}{\sqrt[]{2 α}} \frac{r}{{[s^{(2)} (z)]}^{2}} \cdot \exp (i k_{0} n_{0} z) \exp [- \frac{r^{2}}{2 s^{(2)} (z)}] (1 + \frac{σ}{z \sqrt[]{α}}) \cdot \\ \exp (- iσ) ex p (iφ), (10) \end{matrix} \end{matrix}

式中:E₊为电矢量的左旋圆偏振分量;E_-为电矢量的右旋圆偏振分量;E_z 为电矢量的z分量;r为旋光晶体中某点的极坐标;z为光在旋光晶体中的传播距离;参数α= $\begin{matrix} k_{0}^{2} \end{matrix} \begin{matrix} n_{0}^{2} \end{matrix}$ ;s⁽²⁾(z)=s²+iz/ $\begin{matrix} \sqrt[]{α} \end{matrix}$ 为随传播距离z变化的光场束腰半径的平方;σ= $\begin{matrix} κ_{xyz}^{(2)} \end{matrix} \begin{matrix} k_{0}^{2} \end{matrix}$ z描述了晶体的旋光性对光波纵向传播常数的影响。若忽略BSO晶体旋光性的影响,可令描述旋光性强弱的三阶赝张量元 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ =0,即σ=0,则E_-(r,φ,z)=0,左旋圆偏振高斯光束在晶体中传播时仍然只有左旋圆偏振分量;若考虑BSO晶体的旋光性对二阶非线性电极化的微扰作用,则由于 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ ≠0,E_-(r,φ,z)≠0,此时晶体中出现了E_-右旋圆偏振分量,且从(9)式可以看出E_-分量携带2 $\begin{matrix} \bar{h} \end{matrix}$ ( $\begin{matrix} \bar{h} \end{matrix}$ 为约化普朗克常量)的轨道角动量,说明晶体中光场的自旋-轨道角动量发生了耦合。从(8)~(10)式可以看出,左旋圆偏振傍轴高斯光束在BSO晶体中的传播特性和在锗酸铋磁光晶体(BGO晶体)中的传播特性非常类似^[24]。

本文以波长λ=0.633 μm的光为入射光,光束束腰半径设为s=1 μm,BSO晶体^[27]的折射率为n₀=2.54,晶体的三阶赝张量元 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ =-3.897×10^-12 m/V。图1为BSO晶体中光电场的振幅和相位分布。从图1(c2)、(c3)的相位图中可以看出,E_-、E_z分量分别携带2 $\begin{matrix} \bar{h} \end{matrix}$ 、 $\begin{matrix} \bar{h} \end{matrix}$ 的轨道角动量。

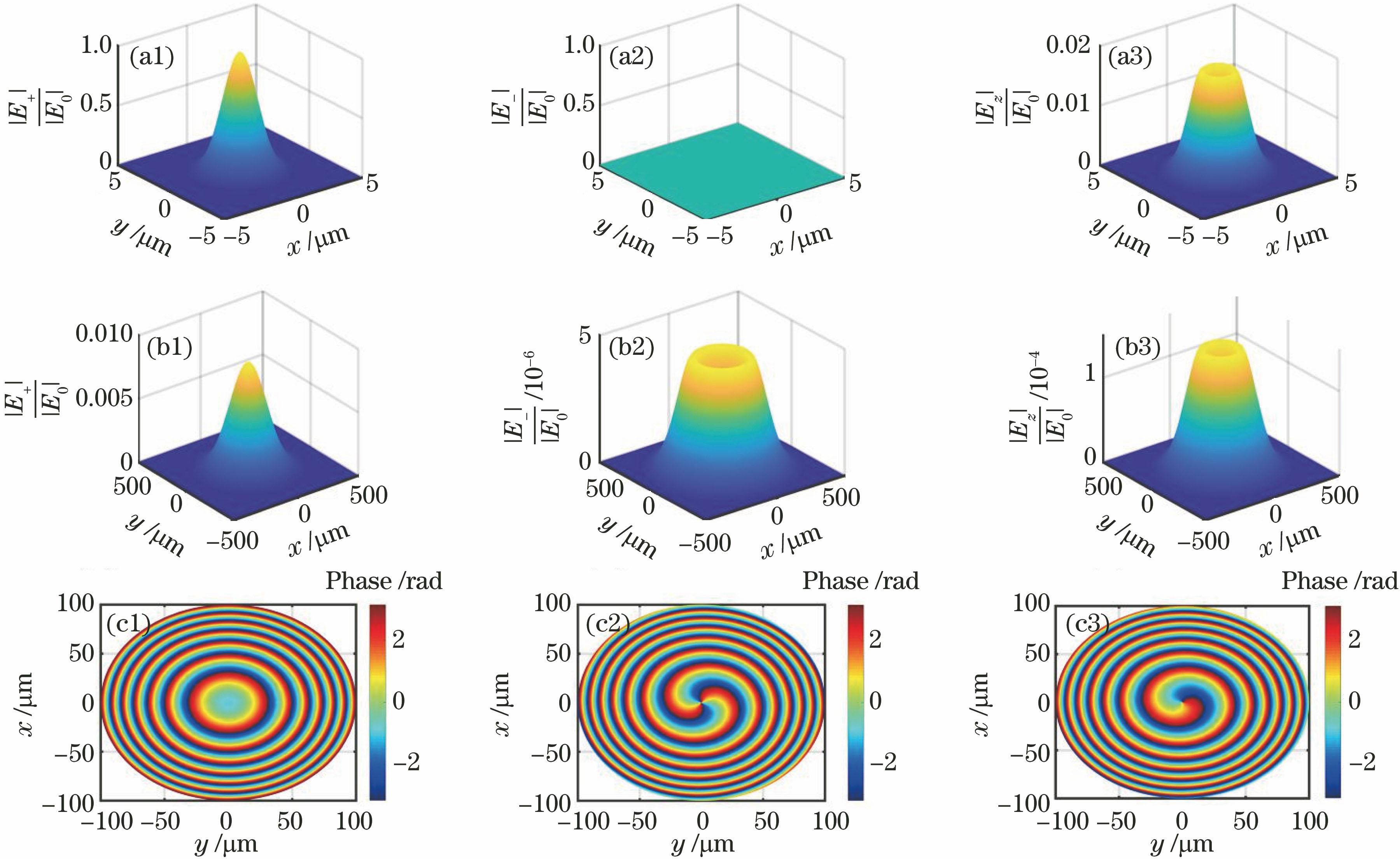
图 1. BSO晶体中光电场的振幅和相位分布。 (a1-a3)在z=0 μm平面上E+、E-和Ez的振幅分布;(b1-b3)在z=3000 μm平面上E+、E-和Ez的振幅分布;(c1-c3)在z=3000 μm平面上E+、E-和Ez的相位分布

Fig. 1. Plots of amplitudes and phases of electric field in BSO crystals. (a1)-(a3) Amplitudes of E+, E-, and Ez on plane of z=0 μm; (b1)-(b3) amplitudes of E+, E-, and Ez on plane of z=3000 μm; (c1)-(c3) phases of E+, E-, and Ez on plane of z=3000 μm

下载图片查看所有图片

在推导出BSO晶体中光电场的基础上,可以研究晶体的旋光性对晶体中光动量的影响。分别采用Minkowski光动量密度g_M=D×B和Abraham光动量密度g_A= $\begin{matrix} \frac{1}{c^{2}} \end{matrix}$ E×H两种形式,其中c为真空中光速,D为电位移矢量,B为磁感应强度矢量,E为电场强度矢量,H为磁场强度矢量。BSO晶体中电位移矢量元为D_μ=ε_μαE_α+ $\begin{matrix} P_{μ}^{(2)} \end{matrix}$ ,磁感应强度为B_j=- $\begin{matrix} \frac{i}{ω} \end{matrix}$ ε_jkl∂_kE_l,磁场强度为H_j=- $\begin{matrix} \frac{i}{μ_{0} ω} \end{matrix}$ ε_jkl∂_kE_l,其中ε_μα为晶体的介电张量元,E_α为光电矢量的α分量, $\begin{matrix} P_{μ}^{(2)} \end{matrix}$ 为二阶非线性电极化强度的μ分量,∂_k为对坐标x_k分量的偏微分,E_l为光电矢量的l分量。结合前面推导出的BSO晶体中的光电场(8)~(10)式,可得

\begin{matrix} \begin{matrix} {g^{A}}_{j} = - \frac{ε_{0}}{2 ω} Im [ε_{jkl} E_{k} ε_{lmn} (\partial_{m} E_{n})^{*}], (11) \\ {g^{M}}_{j} = n_{0}^{2} {g^{A}}_{j} + Δ g_{j}, (12) \\ Δ g_{j} = \frac{ε_{0}}{ω} κ_{xyz}^{(2)} ε_{jkl} Im [ε_{kmn} (\partial_{m} E_{n}) ε_{lpq} (\partial_{p} E_{q})^{*}] 。 (13) \end{matrix} \end{matrix}

式中: $\begin{matrix} g_{j}^{A} \end{matrix}$ 、 $\begin{matrix} g_{j}^{M} \end{matrix}$ 为代表Abraham和Minkowski动量密度的j分量;Δg_j为与旋光性相关的动量密度的j分量;E_k、E_q分别为光电矢量的k、q分量,ε_lmn、ε_lmn及ε_lpq均为Levi-Civita张量元素。

若忽略BSO晶体旋光性的影响,令 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ =0,由(11)~(13)可知,晶体中两种形式的动量密度之间满足g_M= $\begin{matrix} n_{0}^{2} \end{matrix}$ g_A,即Minkowski动量密度与Abraham动量密度的比值为晶体折射率n₀的平方;若将BSO晶体的旋光性视为二阶非线性电极化的微扰,由于 $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ ≠0,则Minkowski动量密度中增加了一项与旋光性相关的动量密度Δg,该项的出现使g_M≠ $\begin{matrix} n_{0}^{2} \end{matrix}$ g_A。由于BSO晶体的旋光性( $\begin{matrix} κ_{xyz}^{(2)} \end{matrix}$ ≠0)会影响到晶体中的光电场,因此旋光性对Abraham动量密度和Minkowski动量密度均有影响。图2给出了Abraham动量密度和Minkowski动量密度及Δg_j在z=3000 μm面上的分布。值得注意的是,Abraham动量密度和Minkowski动量密度的横向分量,即 $\begin{matrix} g_{x}^{A} \end{matrix}$ 、 $\begin{matrix} g_{y}^{A} \end{matrix}$ 、 $\begin{matrix} g_{x}^{M} \end{matrix}$ 、 $\begin{matrix} g_{y}^{M} \end{matrix}$ 的积分值为零,纵向分量 $\begin{matrix} g_{z}^{A} \end{matrix}$ 和 $\begin{matrix} g_{z}^{M} \end{matrix}$ 的体积分即为BSO晶体中的总光动量,Abraham动量 $\begin{matrix} P_{z}^{A} \end{matrix}$ = $\begin{matrix} \int g \end{matrix} \begin{matrix} _{z}^{A} \end{matrix}$ dV,Minkowski动量 $\begin{matrix} P_{z}^{M} \end{matrix}$ = $\begin{matrix} \int g \end{matrix} \begin{matrix} _{z}^{M} \end{matrix}$ dV,总动量沿传播方向z轴正方向,V为晶体体积。Δg_j的横向分量Δg_x和Δg_y的积分结果也均为零,纵向分量Δg_z的积分记为ΔP_z= $\begin{matrix} \int \end{matrix}$ _VΔg_zdV。旋光效应的存在导致Minkowski动量 $\begin{matrix} P_{z}^{M} \end{matrix}$ 和Abraham动量 $\begin{matrix} P_{z}^{A} \end{matrix}$ 的比值不再是晶体折射率n₀的平方,而是满足 $\begin{matrix} P_{z}^{M} \end{matrix}$ = $\begin{matrix} n_{0}^{2} \end{matrix} \begin{matrix} P_{z}^{A} \end{matrix}$ +ΔP_z。

2.2 傍轴高斯光束在BSO晶体中的角动量

在已推导出BSO晶体中光动量的基础上,可以研究光在BSO晶体中的角动量特性。将位置矢量r叉乘动量密度矢量可以得到相应的角动量密度矢量^[28] ,即

\begin{matrix} \begin{matrix} j_{M} = r \times (D \times B), (14) \\ j_{A} = \frac{1}{c^{2}} r \times (E \times H), (15) \end{matrix} \end{matrix}

图 2. 动量密度gjA、gjM及Δgj在z=3000 μm面上的分布。(a1-a3) Abraham动量密度gjA;(b1-b3) Minkowski动量密度gjM;(c1-c3) Δgj

Fig. 2. Plots of momentum density gjA, gjM, and Δgj on plane of z=3000 μm. (a1)-(a3) Abraham momentum density gjA; (b1)-(b3) Minkowski momentum density gjM; (c1)-(c3) Δgj

下载图片查看所有图片

式中:j_M为Minkowski角动量密度;j_A为Abraham角动量密度。将Minkowski和Abraham动量密度代入(14)式和(15)式,即可得高斯光束在BSO晶体中的角动量密度。

从Maxwell方程组出发可以推导得出^[15]

\begin{matrix} \begin{matrix} \frac{d}{dt} \int r \times (D \times B) dV = \int r \times (E \nabla \cdot D - D \times \nabla \times E) dV + \\ \int r \times (H \nabla \cdot B - B \times \nabla \times H) dV, (16) \\ E \nabla \cdot D - D \times \nabla \times E + H \nabla \cdot B - B \times \nabla \times H = \nabla \cdot T, (17) \end{matrix} \end{matrix}

式中:t为时间;T为介质中电磁场动量流密度张量。本文采用Maxwell和赫维赛德(Heaviside)提出的不对称形式 $\begin{matrix} T_{ij}^{M} \end{matrix}$ =E_iD_j- $\begin{matrix} \frac{1}{2} \end{matrix}$ (E·D)δ_ij+H_iB_j- $\begin{matrix} \frac{1}{2} \end{matrix}$ (H·B)δ_ij,其中E_i为光电矢量i分量,D_j为电位移矢量j分量,H_i为磁场强度矢量i分量,B_j为磁感应强度矢量j分量,δ_ij为克罗内克函数。将(16)式改写为^[15,17]

\begin{matrix} \frac{d L_{f}}{dt} = \int Fn dS + \int g dV, (18) \end{matrix}

式中:S为包围体积V的表面;n=n_xe_x+n_ye_y+n_ze_z为垂直表面S向外指出的单位矢量,其中e_x、e_y、e_z为沿坐标轴的三个单位矢量,(n_x,n_y,n_z)为n的方向余弦;L_f= $\begin{matrix} \int \end{matrix}$ _Vr×(D×B)dV为体积V内Minkowski形式的电磁场总角动量;F为角动量流密度张量。当对g的体积分为零时,(18)式为角动量流的连续性方程。可以推导得BSO晶体中

\begin{matrix} g_{j} = - ε_{0} κ_{xyz}^{(2)} ε_{jkl} Re [E_{k} ε_{lmn} (\partial_{m} E_{n})^{*}] 。 (19) \end{matrix}

图3给出了两种形式的角动量密度j_A和j_M及g在z=3000 μm面上的分布。两种角动量密度的横向分量 $\begin{matrix} j_{x}^{A} \end{matrix}$ 、 $\begin{matrix} j_{y}^{A} \end{matrix}$ 、 $\begin{matrix} j_{x}^{M} \end{matrix}$ 、 $\begin{matrix} j_{y}^{M} \end{matrix}$ 的积分结果均为0,因此总角动量也是沿传播方向z轴正方向。同样地,g的横向分量g_x、g_y的积分也均为零。

将BSO晶体的厚度记为Z,晶体的出射端面可以分为z=Z^-和z=Z⁺内外两面,(18)式对时间求平均可以改写为^[17]

\begin{matrix} < \frac{d L_{fz}}{dt} > = Φ (0^{+}) - Φ (Z^{-}) + \int < g_{z} > dV, (20) \end{matrix}

图 3. 角动量密度j及g的各个分量在z=3000 μm平面上的分布。(a1)-(a3) Abraham角动量密度jA的各个分量;(b1)-(b3) Minkowski角动量密度jM的各个分量;(c1)-(c3) g的各个分量

Fig. 3. Plots of components of angular momentum density j and g on plane of z=3000 μm. (a1)-(a3) Components of Abraham angular momentum density jA; (b1)-(b3) components of Minkowski angular momentum density jM; (c1)-(c3) components of g

下载图片查看所有图片

式中:0⁺代表位于晶体内侧的入射端面;Z^-代表位于晶体内侧的出射端面;Φ(z)=- $\begin{matrix} \int \end{matrix}$ _S<F_zz(r_⊥,z,t)>dS表示对时间求平均后流过任意z平面的角动量流,角动量流在晶体出射端的内外表面上是连续的,即Φ(Z^-)=Φ(Z⁺)=Φ(z),其中F_zz(r_⊥,z,t)为角动量流密度张量元。对时间求平均得< $\begin{matrix} \frac{d L_{fz}}{dt} \end{matrix}$ >=0,即光场和晶体的总角动量守恒。对g_z的积分 $\begin{matrix} \int \end{matrix}$ <g_z>dV≠0,说明傍轴高斯光场与BSO晶体之间的角动量发生耦合,J_c(z)=- $\begin{matrix} \int \end{matrix}$ _V<g_z>dV为光场传递给BSO晶体的角动量,因此,光场自身的角动量并不守恒。

3 结论

基于Bi₁₂SiO₂₀晶体研究了高斯光束在旋光晶体中的旋光现象。采用角谱理论推导得出左旋圆偏振傍轴高斯光束在晶体中的光电场表达式;在此基础上,采用Minkowski和Abraham两种动量形式研究了旋光效应的存在对BSO晶体中光动量和角动量的影响。考虑旋光性后的Minkowski动量中包含一项与三阶赝张量 $\begin{matrix} κ_{jkl}^{(2)} \end{matrix}$ 相联系的动量ΔP_z,该项的存在使得Minkowski动量 $\begin{matrix} P_{z}^{M} \end{matrix}$ 和Abraham动量 $\begin{matrix} P_{z}^{A} \end{matrix}$ 的比值不再是晶体折射率n₀的平方,而是满足 $\begin{matrix} P_{z}^{M} \end{matrix}$ = $\begin{matrix} n_{0}^{2} \end{matrix} \begin{matrix} P_{z}^{A} \end{matrix}$ +ΔP_z这一关系式。采用Maxwell和赫维赛德提出的电磁场动量流密度张量和Minkowski形式的动量,分析了BSO晶体中的角动量流,发现光场和BSO晶体的总角动量守恒,但光场与BSO晶体之间角动量发生耦合,J_c(z)=- $\begin{matrix} \int \end{matrix}$ <g_z>dV为光场传递给晶体的角动量。

参考文献

[1] Minkowski H. The fundamental equations for electromagnetic processes in moving bodies[J]. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1908: 53-111.

[2] Abraham M. On the electrodynamics of moving bodies[J]. Rendiconti del Circolo Matematico di Palermo, 1909, 28: 1-28.

[3] Baxter C, Babiker M, Loudon R. Canonical approach to photon pressure[J]. Physical Review A, 1993, 47(2): 1278-1287.

[4] Hinds E A, Barnett S M. Momentum exchange between light and a single atom: Abraham or Minkowski?[J]. Physical Review Letters, 2009, 102(5): 050403.

[5] Barnett S M, Loudon R. The enigma of optical momentum in a medium[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2010, 368(1914): 927-939.

[6] Antonoyiannakis M I, Pendry J B. Electromagnetic forces in photonic crystals[J]. Physical Review B, 1999, 60(4): 2363-2374.

[7] Mansuripur M. Radiation pressure and the linear momentum of the electromagnetic field[J]. Optics Express, 2004, 12(22): 5375-5401.

[8] Mansuripur M. Radiation pressure and the linear momentum of light in dispersive dielectric media[J]. Optics Express, 2005, 13(6): 2245-2250.

[9] Mansuripur M. Radiation pressure and the linear momentum of the electromagnetic field in magnetic media[J]. Optics Express, 2007, 15(21): 13502-13518.

[10] Moloney J V. Interaction of light with subwavelength structures[J]. Optics & Photonics News, 2003, 14(3): 56-61.

[11] Kemp B A, Kong J A, Grzegorczyk T M. Reversal of wave momentum in isotropic left-handed media[J]. Physical Review A, 2007, 75(5): 053810.

[12] Feigel A. Quantum vacuum contribution to the momentum of dielectric media[J]. Physical Review Letters, 2004, 92(2): 020404.

[13] 李东华, 蒲继雄, 王喜庆. 透明平板在高斯光束照射下辐射压力的研究[J]. 中国激光, 2011, 38(s1): s102008.

Li D H, Pu J X, Wang X Q. Investigation on the radiation forces upon a transparent plate by a Gaussian beam[J]. Chinese Journal of Lasers, 2011, 38(s1): s102008.

[14] Ciattoni A. Crosignani B, di Porto P. Vectorial theory of propagation in uniaxially anisotropic media[J]. Journal of the Optical Society of America A, 2001, 18(7): 1656-1661.

[15] Ciattoni A, Cincotti G, Palma C. Angular momentum dynamics of a paraxial beam in a uniaxial crystal[J]. Physical Review E, 2003, 67(3): 036618.

[16] 魏功祥, 刘晓娟, 刘云燕, 等. 光的自旋和轨道角动量[J]. 激光与光电子学进展, 2014, 51(10): 100004.

Wei G X, Liu X J, Liu Y Y, et al. Spin and orbital angular momentum of light[J]. Laser & Optoelectronics Progress, 2014, 51(10): 100004.

[17] Lu X C, Chen L X. Spin-orbit interactions of a Gaussian light propagating in biaxial crystals[J]. Optics Express, 2012, 20(11): 11753-11766.

[18] YarivA, YehP. Optical waves in crystal: propagation and control of laser radiation[M]. Hoboken: John Wiley & Sons, Inc., 1984: 94- 103.

[19] 过巳吉. 非线性光学[M]. 西安: 西北电讯工程学院出版社, 1986: 157- 161.

Guo SJ. Nonlinear optics[M]. Xi'an: Northwest Telecommunication Engineering Institute Press, 1986: 157- 161.

[20] Yariv A, Lotspeich J F. Coupled-mode analysis of light propagation in optically active crystals[J]. Journal of the Optical Society of America, 1982, 72(2): 273-277.

[21] 许婕, 陈理想, 郑国梁, 等. 双折射晶体中旋光效应的耦合波理论[J]. 物理学报, 2007, 56(8): 4615-4621.

Xu J, Chen L X, Zheng G L, et al. Wave coupling theory of optical activity in birefringent crystal[J]. Acta Physica Sinica, 2007, 56(8): 4615-4621.

[22] Ciattoni A, Palma C. Optical propagation in uniaxial crystals orthogonal to the optical axis: paraxial theory and beyond[J]. Journal of the Optical Society of America A, 2003, 20(11): 2163-2171.

[23] Laudau LD, Lifshitz EM. Electrodynamics of continuous media[M]. Oxford: Pergamon Press, 1984: 363.

[24] Lu X C, Chen L X. Vortex generation and inhomogeneous Faraday rotation of a nonparaxial Gaussian beam in isotropic magneto-optic crystals[J]. Optics Letters, 2014, 39(13): 3728-3731.

[25] 陈纲, 廖理几. 晶体物理学基础[M]. 北京: 科学出版社, 1992: 474- 492.

ChenG, Liao LJ. Foundation of crystal physics[M]. Beijing: Science Press, 1992: 474- 492.

[26] Ciattoni A, Cincotti G, Palma C. Circularly polarized beams and vortex generation in uniaxial media[J]. Journal of the Optical Society of America A, 2003, 20(1): 163-171.

[27] Petrov MP, Stepanov SI, Khomenko AV. Photo refractive crystals in coherent optical systems[M]. Berlin, Heidelberg: Springer, 1991, 59: 233.

[28] Barnett S M. Optical angular-momentum flux[J]. Journal of Optics B: Quantum and Semiclassical Optics, 2002, 4(2): S7-S16.

1 引言

2 理论

2.1 傍轴高斯光束在BSO晶体中的光电场和光动量

2.2 傍轴高斯光束在BSO晶体中的角动量

3 结论

陈舒婷, 郭昊旭, 邱晓东, 陈理想. 旋光效应对Bi₁₂SiO₂₀晶体中光动量及角动量的影响[J]. 激光与光电子学进展, 2019, 56(13): 132601. Shuting Chen, Haoxu Guo, Xiaodong Qiu, Lixiang Chen. Influence of Optical Activity on Optical Momentum and Angular Momentum in Bi₁₂SiO₂₀ Crystals[J]. Laser & Optoelectronics Progress, 2019, 56(13): 132601.

旋光效应对Bi₁₂SiO₂₀晶体中光动量及角动量的影响下载： 1002次

1 引言

2 理论

2.1 傍轴高斯光束在BSO晶体中的光电场和光动量

图 1. BSO晶体中光电场的振幅和相位分布。 (a1-a3)在z=0 μm平面上E+、E-和Ez的振幅分布;(b1-b3)在z=3000 μm平面上E+、E-和Ez的振幅分布;(c1-c3)在z=3000 μm平面上E+、E-和Ez的相位分布

Fig. 1. Plots of amplitudes and phases of electric field in BSO crystals. (a1)-(a3) Amplitudes of E+, E-, and Ez on plane of z=0 μm; (b1)-(b3) amplitudes of E+, E-, and Ez on plane of z=3000 μm; (c1)-(c3) phases of E+, E-, and Ez on plane of z=3000 μm

2.2 傍轴高斯光束在BSO晶体中的角动量

图 2. 动量密度gjA、gjM及Δgj在z=3000 μm面上的分布。(a1-a3) Abraham动量密度gjA;(b1-b3) Minkowski动量密度gjM;(c1-c3) Δgj

Fig. 2. Plots of momentum density gjA, gjM, and Δgj on plane of z=3000 μm. (a1)-(a3) Abraham momentum density gjA; (b1)-(b3) Minkowski momentum density gjM; (c1)-(c3) Δgj

图 3. 角动量密度j及g的各个分量在z=3000 μm平面上的分布。(a1)-(a3) Abraham角动量密度jA的各个分量;(b1)-(b3) Minkowski角动量密度jM的各个分量;(c1)-(c3) g的各个分量

Fig. 3. Plots of components of angular momentum density j and g on plane of z=3000 μm. (a1)-(a3) Components of Abraham angular momentum density jA; (b1)-(b3) components of Minkowski angular momentum density jM; (c1)-(c3) components of g

3 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

旋光效应对Bi12SiO20晶体中光动量及角动量的影响 下载： 1002次

1 引言

2 理论

2.1 傍轴高斯光束在BSO晶体中的光电场和光动量

图 1. BSO晶体中光电场的振幅和相位分布。 (a1-a3)在z=0 μm平面上E+、E-和Ez的振幅分布;(b1-b3)在z=3000 μm平面上E+、E-和Ez的振幅分布;(c1-c3)在z=3000 μm平面上E+、E-和Ez的相位分布

Fig. 1. Plots of amplitudes and phases of electric field in BSO crystals. (a1)-(a3) Amplitudes of E+, E-, and Ez on plane of z=0 μm; (b1)-(b3) amplitudes of E+, E-, and Ez on plane of z=3000 μm; (c1)-(c3) phases of E+, E-, and Ez on plane of z=3000 μm

2.2 傍轴高斯光束在BSO晶体中的角动量

图 2. 动量密度gjA、gjM及Δgj在z=3000 μm面上的分布。(a1-a3) Abraham动量密度gjA;(b1-b3) Minkowski动量密度gjM;(c1-c3) Δgj

Fig. 2. Plots of momentum density gjA, gjM, and Δgj on plane of z=3000 μm. (a1)-(a3) Abraham momentum density gjA; (b1)-(b3) Minkowski momentum density gjM; (c1)-(c3) Δgj

图 3. 角动量密度j及g的各个分量在z=3000 μm平面上的分布。(a1)-(a3) Abraham角动量密度jA的各个分量;(b1)-(b3) Minkowski角动量密度jM的各个分量;(c1)-(c3) g的各个分量

Fig. 3. Plots of components of angular momentum density j and g on plane of z=3000 μm. (a1)-(a3) Components of Abraham angular momentum density jA; (b1)-(b3) components of Minkowski angular momentum density jM; (c1)-(c3) components of g

3 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

旋光效应对Bi₁₂SiO₂₀晶体中光动量及角动量的影响下载： 1002次