Electromagnetic chirality induced by graphene inclusions in multilayered metamaterials

Carlo Rizza; Elia Palange; Alessandro Ciattoni

doi:doi:10.1364/PRJ.2.000121

Photonics Research, 2014, 2 (5): 05000121, Published Online: Nov. 5, 2014

Electromagnetic chirality induced by graphene inclusions in multilayered metamaterials Download： 833次

论文大纲

Carlo Rizza ^1,2Elia Palange ³Alessandro Ciattoni ^2,*

Author Affiliations

¹ Dipartimento di Scienza e Alta Tecnologia, Università dell’Insubria, via Valleggio 11, 22100 Como, Italy

² Consiglio Nazionale delle Ricerche, CNR-SPIN, 67100 Coppito L’Aquila, Italy

³ Dipartimento di Scienze fisiche e chimiche, Università di L’Aquila, via Vetoio, 67100 Coppito L’Aquila, Italy

Metamaterials Multilayers Plasmonics

Abstract

We theoretically investigate the electromagnetic response of a novel class of multilayered metamaterials obtained by alternating graphene sheets and dielectric layers, the whole structure not exhibiting a plane of reflection symmetry along the stacking direction. We show that the electromagnetic response of the structure is characterized by a magneto-electric coupling described by an effective chiral parameter. Exploiting the intrinsic tunability of graphene–light coupling, we prove that one can tune both the dielectric and the chiral electromagnetic response by varying the graphene chemical potential through external voltage gating.

1. INTRODUCTION

Graphene, a one-atom-thick layer of carbon atoms arranged in a honeycomb lattice, shows a wide range of unique properties. For example, graphene exhibits high thermal and electric conductivity, a high optical damage threshold, and high third-order optical nonlinearities ^[1]. Recently, many graphene-based photonic and optoelectronic devices have been proposed and developed, such as plasmonic waveguides ^{[24" target="_self" style="display: inline;">–4]}, frequency multipliers ^[5], modulators ^[6,7], photodetectors ^[8], and polarizers ^[9]. In the context of metamaterials, Vakil and Engheta ^[10] have theoretically proposed a setup in which a graphene sheet is a one-atom-thick platform for achieving the desired infrared metamaterials and transformation optical devices. On the other hand, several researchers have investigated multilayer structures composed of stacked graphene sheets separated by thin dielectric layers ^{[11–15" target="_self" style="display: inline;">–15]}. A noteworthy advantage of such proposed metamaterials is the overall tunability of the electromagnetic response, which is entailed by the dependence of the graphene conducibility on the chemical potential. For example, the graphene-based metamaterial response can be tailored from elliptic birefringent to hyperbolic by varying the graphene chemical potential through an external gate voltage ^[12].

In this paper, we propose a novel class of graphene-based metamaterials exhibiting a marked chiral electromagnetic response, and we demonstrate that such a nonlocal effect can be tuned by varying the chemical potential of graphene sheets. More precisely, we consider propagation of transverse magnetic (TM) waves through a multilayer periodic structure not exhibiting a plane of reflection symmetry whose unit cell comprises $N$ layers of different dielectric materials alternated with $N$ graphene sheets. Exploiting a suitable multiscale approach in which the period-to-wavelength ratio is the small expansion parameter, we obtain the constitutive equations describing the spatially nonlocal metamaterial response. Specifically, we refine the standard effective medium theory (EMT) by deriving higher-order contributions predicting, in particular, an overall medium chiral response for those layer thicknesses not fully assuring homogenization. Generally, a reciprocal or chiral magneto-electric coupling is a consequence of the medium 3D or 2D chirality; namely, the underlying constituents (organic molecules, proteins, “meta-molecules,” etc.) exhibit mirror asymmetry ^[16]. Chirality can produce noteworthy effects such as optical rotation and negative refraction ^[17]. On the other hand, the configuration we consider in this paper lacks a plane of mirror symmetry, causing an overall chiral medium response that is tunable due to the presence of graphene sheets. It is worth stressing that usually considered bilayer metal–dielectric structures ^[18,19] and graphene-based metamaterials (considered in Refs. ^{[1214" target="_self" style="display: inline;">–14]}, where the metamaterial unit cell consists of a graphene sheet placed on top of a dielectric material) show electromagnetic response strongly affected by second-order spatial dispersion, which, however, does not yield electromagnetic chirality since the structure geometry admits a plane of mirror symmetry.

The paper is organized as follows. In Section 2 we develop an effective medium approach up to the first order in the homogenization parameter for investigating effective spatial dispersion produced by incomplete homogenization. In Section 3 we discuss the electromagnetic chirality produced by the effective spatial dispersion in the presence of medium mirror asymmetry. In Section 4 we show that graphene can both break the mirror symmetry of a layered medium and provide tunability for the so-induced effective electromagnetic chiral response. In Section 5 we draw our conclusions.

2. EFFECTIVE MEDIUM APPROACH

Let us consider TM waves propagating in a graphene-based metamaterial whose underlying multilayered structure has a unit cell obtained by stacking, along the $z$ axis, $N$ graphene sheets separated by $N$ layers of different media of thicknesses $d_{j}$ ( $j = 1,2, 3, \dots, N$ ) (see Fig. 1, where the case in which $N = 2$ is reported). The electromagnetic field amplitudes $E = E_{x} (x, z) {\hat{e}}_{x} + E_{z} (x, z) {\hat{e}}_{z}$ , $H = H_{y} (x, z) {\hat{e}}_{y}$ associated with monochromatic TM waves (the time dependence $\exp (- i ω t)$ has been assumed where $ω$ is the angular frequency) satisfy Maxwell’s equations where $ϵ_{x}$ and $ϵ_{z}$ are the $x$ component and the $z$ component of the dielectric permittivity tensor, respectively, and both are periodic functions of period $d = \sum_{j = 1}^{N} d_{j}$ . Here, the $j$ th graphene sheet response is described by the surface conductivity $σ_{j}$ so that the surface current $K_{x j} = σ_{j} E_{x}$ yields a delta-like contribution to $ϵ_{x}$ , which is $i σ_{j} / (ω ϵ_{0}) δ (z - z_{j})$ , $z_{j}$ being the sheet position ^[13] (see below). Note that the surface conductivities $σ_{j}$ can assume different values in order to encompass the relevant situation in which the graphene can be locally tuned or substituted with more general bidimensional hetero-structures.

Sketch of graphene-based metamaterial unit cell. ϵj and dj (j=1,2) are the relative dielectric permittivities and the thicknesses of the dielectric layers, respectively.

Fig. 1. Sketch of graphene-based metamaterial unit cell. $ϵ_{j}$ and $d_{j}$ ( $j = 1,2$ ) are the relative dielectric permittivities and the thicknesses of the dielectric layers, respectively.

下载图片查看所有图片

In order to obtain an effective medium description of the electromagnetic propagation in the regime in which the ratio between the period $d$ and the wavelength $λ$ is small, we exploit a standard and rather general multiscale technique ^[20,21] holding for very general $ϵ_{x} (z)$ and $ϵ_{z} (z)$ periodic profiles (which we will later specialize to the considered graphene-based multilayer). Accordingly we introduce the parameter $η = d / λ ≪ 1$ and the fast coordinate $Z = z / η$ , and, aimed at isolating the slowly and rapidly varying contributions, we consider the Fourier series of $ϵ_{x}$ and $ϵ_{z}^{- 1}$ , namely $ϵ_{x} = 〈 ϵ_{x} 〉 + δ ϵ_{x}$ , $ϵ_{z}^{- 1} = 〈 ϵ_{z}^{- 1} 〉 + δ ϵ_{z}^{(- 1)}$ , where $〈 f 〉$ is the mean value of the function $f$ and where $k_{0} = 2 π / λ$ . The basic Ansatz of our approach is given by where $\bar{A} (x, z)$ and $δ A (x, z, Z)$ are the slowly (averaged) and rapidly varying parts of each electromagnetic field component $A$ , respectively ( $A = E_{x}, E_{z}, H_{y}$ ). The considered Ansatz, where each field component is a Taylor expansion up to first order in $η$ , has been suitably chosen to self-consistently assure that finite and nontrivial results are obtained in the asymptotic $η \to 0$ limit. Substituting the Fourier series of $ϵ_{x}$ and $ϵ_{z}^{- 1}$ and the Ansatz of Eqs. (3) into Maxwell equations (1), after separating the slowly and rapidly varying contributions, we obtain the coupled equations and It is important to stress that no terms have been neglected when deriving Eqs. (4), whereas only the leading contributions (the lowest powers of $η$ ) has been retained to obtain Eqs. (5). After integration on $Z$ and using Eqs. (2), Eqs. (5) yield the rapidly varying parts of the field amplitudes as functions of the slow ones, i.e., Finally, substituting Eqs. (6) into Eqs. (4), we get where $Z_{0} = \sqrt{μ_{0} / ϵ_{0}}$ is the vacuum impedance, and $ϵ_{x}^{(eff)} = 〈 ϵ_{x} 〉$ , $ϵ_{z}^{(eff)} = {〈 ϵ_{z}^{- 1} 〉}^{- 1}$ and It is evident that in the limit $η \to 0$ the parameter $τ^{(eff)}$ vanishes and the multiscale approach considered in this paper reproduces the results of the well-known standard EMT ^[18]. Furthermore, it is worth noting that in the case in which the structure admits mirror symmetry with respect a specific plane $z = z_{0}$ , i.e., the relations $ϵ_{x} (z) = ϵ_{x} (- z + z_{0})$ and $ϵ_{z} (z) = ϵ_{z} (- z + z_{0})$ hold, it is straightforward to prove that the dielectric Fourier coefficients are such that $a_{- n} = \exp (i 2 π n z_{0} / d) a_{n}$ and $b_{- n} = \exp (i 2 π n z_{0} / d) b_{n}$ so that $a_{- n} b_{n} = a_{n} b_{- n}$ and the series of Eq. (8) provides a vanishing $τ^{(eff)}$ . Therefore, the slowly varying and leading electromagnetic field can experience the effect of the novel terms proportional to $τ^{(eff)}$ in the effective Maxwell equations of Eq. (7) only if the multilayer does not exhibit an inversion center.

3. SPATIAL DISPERSION AND CHIRALITY

Comparing the second and the third of Eqs. (7) with the standard equations $\partial_{z} {\bar{H}}_{y} = i ω {\bar{D}}_{x}$ , $\partial_{x} {\bar{H}}_{y} = - i ω ϵ_{0} {\bar{D}}_{z}$ and using the third of Eqs. (7) to substitute for the magnetic field derivative, we obtain which are the structure effective constitutive relations. Note that Eqs. (9) contain terms proportional to the first and second $x$ -spatial derivatives of the field components, terms usually arising when dealing with a weakly spatially nonlocal medium. Exploiting the fact that the effective Maxwell’s equations are invariant with respect to transformation ${\bar{D}}_{x}^{'} = {\bar{D}}_{x} - \partial_{z} Q$ , ${\bar{D}}_{z}^{'} = {\bar{D}}_{z} + \partial_{x} Q$ , and ${\bar{H}}_{y}^{'} = {\bar{H}}_{y} - i ω Q$ (where $Q (x, z)$ is an arbitrary function), after setting $Q = - ϵ_{0} τ^{(eff)} / k_{0} {\bar{E}}_{x}$ , we obtain the equivalent effective constitutive relations Therefore, for $η ≪ 1$ (quasi-homogenization regime), the terms proportional to $τ^{(eff)}$ in Eqs. (10) yield an effective bianisotropic medium response (i.e., of the form $D = ϵ_{0} ϵ E + (1 / c) (χ^{T} - i κ^{T}) H$ , $B = μ_{0} μ H + (1 / c) (χ + i κ) E$ ^[22]) with nonreciprocity dyadic $χ = 0$ and chirality dyadic $κ$ not vanishing (with only nonvanishing component $κ_{21} = - τ^{(eff)}$ ). Therefore, for TM waves, the multilayer mirror asymmetry provides the medium an effective anisotropic chiral response.

4. GRAPHENE-INDUCED TUNABLE ELECTROMAGNETIC CHIRALITY

Graphene sheets can both break the mirror symmetry and provide the structure electromagnetic tunability. In order to discuss this point, we consider a bilayer structure whose unit cell comprises two dielectric layers separated by a graphene sheet. The dielectric permittivities of such a structure can be written, within the unit cell $0 \leq z < d$ , as $ϵ_{x} = Ξ (z) + (i σ_{1} / ω ϵ_{0}) δ (z - d_{1})$ and $ϵ_{z} = Ξ (z)$ , where $Ξ (z) = ϵ_{1} Π ((z - d_{1} / 2) / d_{1}) + ϵ_{2} Π ((z - d_{2} / 2 - d_{1}) / d_{2})$ , $Π (ζ)$ is the rectangular function ( $Π (ζ) = 0$ if $| ζ | > 1 / 2$ , $Π (ζ) = 1 / 2$ if $| ζ | = 1 / 2$ , and $Π (ζ) = 1$ if $| ζ | < 1 / 2$ ), $δ (ζ)$ is the Dirac delta function, and $σ_{1}$ is the surface conductivity of the graphene layer. In this model, the graphene sheet is infinitesimally thin, and the current it supports is along the $x$ direction, thus solely affecting the bilayer $x$ component of the permittivity tensor. In addition, it is evident that the positioning of the graphene sheets provides the structure the lack of a mirror symmetry plane along the stacking direction. The structure effective parameters are easily evaluated and are where the expression of $τ^{(eff)}$ is obtained after the straightforward summation of the series in Eq. (8). Evidently $τ^{(eff)}$ vanishes if there is no graphene ( $σ_{1} = 0$ , discussed in Refs. ^[18,19]) or if the dielectrics are identical ( $ϵ_{1} = ϵ_{2}$ , discussed in Refs. ^{[1214" target="_self" style="display: inline;">–14]}) since in both situations the structure does show a mirror symmetry plane. It is worth noting that the proposed method for producing electromagnetic chirality using graphene sheets is very efficient since the parameter $τ^{(eff)}$ of Eqs. (11) can easily be tuned and enhanced by acting on $ϵ_{z}^{(eff)}$ (which can be set to have a large magnitude through tailoring the multilayer structure) and on the dielectric inhomogeneity $((1 / ϵ_{2}) - (1 / ϵ_{1}))$ .

In the following numerical examples, we choose the wavelength $λ = 10.71 μm$ and the layer dielectric permittivities $ϵ_{1} = - 1.87 + 0.16 i$ and $ϵ_{2} = 2.25$ associated to silicon carbide (SiC) ^[23] and PMMA ^[24], respectively. In addition we adopt the semiclassical expression for the graphene conductivity $σ_{1}$ holding if $| μ_{c} | ≫ K_{b} T$ ( $μ_{c}$ is the chemical potential, $K_{b}$ is the Boltzmann’s constant, and $T$ is the temperature) and obtained by taking into account the inter- and intra-band contributions (see Eqs. (4) and (5) in Ref. ^[25]). Note that the graphene surface conductivity depends on the frequency $ω$ , the chemical potential $μ_{c}$ , the temperature $T$ , and the phenomenological scattering rate $Γ$ . Here we assume $T = 300 K$ and $Γ = 0.43 meV$ . In addition, setting $d_{1} = d_{2}$ , the effective permittivity $z$ component is $ϵ_{z}^{(eff)} = - 18.43 + 9.60 i$ , and it is not affected by the chemical potential, whereas the effective permittivity $x$ component $ϵ_{x}^{(eff)}$ and the chiral parameter $τ^{(eff)}$ can be tuned by varying the graphene chemical potential through external voltage gating.

In Fig. 2, we report the real (solid line) and imaginary (dashed line) parts of $ϵ_{x}^{(eff)}$ and $τ^{(eff)}$ , respectively, as functions of $μ_{c}$ for $η = 1 / 15$ . The tunability of the overall electromagnetic response is evident, and it is also remarkable that in this case a transition from a hyperbolic behavior to an anisotropic negative dielectric one occurs: the real part of the $x$ component of the dielectric permittivity $ϵ_{x}^{(eff)}$ is positive in the region $0.1 eV < μ_{c} < 0.2 eV$ [shadow area in Fig. 2(a)], and it is negative in the region $μ_{c} > 0.2 eV$ , whereas $Re (ϵ_{z}^{(eff)})$ is negative everywhere.

Fig. 2. Effective parameters (a) $ϵ_{x}^{(eff)}$ and (b) $τ^{(eff)}$ as functions of the graphene chemical potential $μ_{c}$ .

下载图片查看所有图片

In order to check and discuss the predictions of our multiscale approach, we here consider the scattering process of TM waves by a graphene-based metamaterial slab lying in the region $0 < z < L$ , which, using the standard transfer matrix method, admits full analytical description. Accordingly we evaluate the exact optical transfer function (OTF) defined as $OTF = H_{y}^{(t)} / H_{y}^{(i)}$ , where $H_{y}^{(i)}$ and $H_{y}^{(t)}$ are the amplitudes of the incident and transmitted magnetic fields evaluated at $z = 0$ and $z = L$ , respectively, and where the $x$ dependence $\exp (i k_{x} x)$ has been assumed ( $k_{x}$ is the transverse component of the wave vector). On the other hand, the system of Eqs. (7) together with Eqs. (6) can be solved to obtain the OTF in the quasi-homogenized regime. In Fig. 3 we compare the exact OTF (solid lines) with those predicted by our multiscale approach (dashed lines) and by the standard EMT (dash-circle lines) for $L = 4.01 μm$ , $η = 1 / 8$ , and $μ_{c} = 0.3 eV$ . In this example, the $x$ component of dielectric permittivity and the chiral coefficient are $ϵ_{x}^{(eff)} = 0.095 + 0.079 i$ and $τ^{(eff)} = 0.17 - 0.079 i$ , respectively. We note that our nonlocal multiscale approach is in good agreement with the exact OTF [both predict a resonance at $k_{x} = 1.55 k_{0}$ as shown in Fig. 3(a)], whereas the discrepancies between EMT and exact approach predictions (evidently expected in the not fully homogenized regime at $η = 1 / 8$ ) prove that the predicted nonlocal mechanisms do affect the electromagnetic medium response. Note also that such discrepancies are more pronounced around the resonance peak typical of the chosen background hyperbolic metamaterial ^[26], which is shifted and squeezed by the novel nonlocal mechanisms.

Comparison among the OTFs as evaluated from the exact matrix method (solid lines), from the standard EMT (dashed-circle lines), and from the nonlocal multiscale EMT (dashed lines). The functions MTF and PTF are related to the OTF by the relation OTF(kx)=MTF(kx) exp[iPTF(kx)] (i.e., MTF and PTF are the modulus and phase of OTF).

Fig. 3. Comparison among the OTFs as evaluated from the exact matrix method (solid lines), from the standard EMT (dashed-circle lines), and from the nonlocal multiscale EMT (dashed lines). The functions MTF and PTF are related to the OTF by the relation $OTF (k_{x}) = MTF (k_{x}) \exp [i PTF (k_{x})]$ (i.e., MTF and PTF are the modulus and phase of OTF).

下载图片查看所有图片

5. CONCLUSION

In conclusion we have shown that a multilayer structure not exhibiting mirror symmetry along the stacking direction, in the quasi-homogenized regime, provides anisotropic chiral response, which is generally absent in standard bilayer metamaterials, in turn tunable through the graphene chemical potential.

References

[1] Q. Bao, K. P. Loh. Graphene photonics, plasmonics, and broadband optoelectronic devices. ACS Nano, 2012, 6: 3677-3694.

[2] S. A. Mikhailov, K. Ziegler. New electromagnetic mode in graphene. Phys. Rev. Lett., 2007, 99: 016803.

[3] M. Jablan, H. Buljan, M. Soljacic. Plasmonics in graphene at infrared frequencies. Phys. Rev. B, 2009, 80: 245435.

[4] F. H. L. Koppens, D. E. Chang, F. J. G. de Abajo. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett., 2011, 11: 3370-3377.

[5] S. A. Mikhailov, K. Ziegler. Nonlinear electromagnetic response of graphene: frequency multiplication and the self-consistent-field effects. J. Phys. Condens. Matter, 2008, 20: 384204.

[6] M. Liu, X. Yin, E. Ulin-Avila, B. Geng, T. Zentgraf, L. Ju, F. Wang, X. Zhang. A graphene-based broadband optical modulator. Nature, 2011, 474: 64-67.

[7] M. Tamagnone, A. Fallahi, J. R. Mosig, J. Perruisseau-Carrier. Fundamental limits and near-optimal design of graphene modulators and non-reciprocal devices. Nat. Photonics, 2014, 8: 556-563.

[8] T. Mueller, F. N. Xia, P. Avouris. Graphene photodetectors for high-speed optical communications. Nat. Photonics, 2010, 4: 297-301.

[9] Q. Bao, H. Zhang, B. Wang, Z. Ni, C. H. Y. X. Lim, Y. Wang, D. Y. Tang, K. P. Loh. Broadband graphene polarizer. Nat. Photonics, 2011, 5: 411-415.

[10] A. Vakil, N. Engheta. Transformation optics using graphene. Science, 2011, 332: 1291-1294.

[11] A. Andryieuski, A. V. Lavrinenko, D. N. Chigrin. Graphene hyperlens for terahertz radiation. Phys. Rev. B, 2012, 86: 121108(R).

[12] I. V. Iorsh, I. S. Mukhin, I. V. Shadrivov, P. A. Belov, Y. S. Kivshar. Hyperbolic metamaterials based on multilayer graphene structures. Phys. Rev. B, 2013, 87: 075416.

[13] M. A. K. Othman, C. Guclu, F. Capolino. Graphene-based tunable hyperbolic metamaterials and enhanced near-field absorption. Opt. Express, 2013, 21: 7614-7632.

[14] M. A. K. Othman, C. Guclu, F. Capolino. Graphene–dielectric composite metamaterials: evolution from elliptic to hyperbolic wavevector dispersion and the transverse epsilon-near-zero condition. J. Nanophoton., 2013, 7: 073089.

[15] A. Madani, S. Zhong, H. Tajalli, S. R. Entezar, A. Namdar, Y. Ma. Tunable metamaterials made of graphene-liquid crystal multilayers. Prog. Electromagn. Res., 2013, 143: 545-558.

[16] LandauL. D.LifshitzE. M., Electrodynamics of Continuous Media (Pergamon, 1960).

[17] ZouhdiS.SihvolaA.VinogradovA. P., Metamaterials and Plasmonics: Fundamentals, Modelling, Applications (Springer-Verlag, 2008).

[18] J. Elser, V. A. Podolskiy, I. Salakhutdinov, I. Avrutsky. Nonlocal effects in effective-medium response of nanolayered metamaterials. Appl. Phys. Lett., 2007, 90: 191109.

[19] A. A. Orlov, P. M. Voroshilov, P. A. Belov, Y. S. Kivshar. Engineered optical nonlocality in nanostructured metamaterials. Phys. Rev. B, 2011, 84: 045424.

[20] C. Rizza, A. Ciattoni. Effective medium theory for Kapitza stratified media: diffractionless propagation. Phys. Rev. Lett, 2013, 110: 143901.

[21] C. Rizza, A. Ciattoni. Kapitza homogenization of deep gratings for designing dielectric metamaterials. Opt. Lett., 2013, 38: 3658-3660.

[22] I. V. Semchenkoy, S. A. Khakhomovy, S. A. Tretyakovzx, A. H. Sihvola, E. A. Fedosenkoy. Reflection and transmission by a uniaxially bi-anisotropic slab under normal incidence of plane waves. J. Phys. D, 1998, 31: 2458-2464.

[23] PalikE. D., Handbook of Optical Constants of Solids (Academic, 1985).

[24] R. T. Graf, F. Eng, J. L. Koenig, H. Ishida. Polarization modulation Fourier transform infrared ellipsometry of thin polymer films. Appl. Spectrosc., 1986, 40: 498-503.

[25] G. W. Hanson. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys., 2008, 103: 064302.

[26] X. Li, S. He, Y. Jin. Subwavelength focusing with a multilayered Fabry–Perot structure at optical frequencies. Phys. Rev. B, 2007, 75: 045103.

1. INTRODUCTION

2. EFFECTIVE MEDIUM APPROACH

3. SPATIAL DISPERSION AND CHIRALITY

4. GRAPHENE-INDUCED TUNABLE ELECTROMAGNETIC CHIRALITY

5. CONCLUSION

Carlo Rizza, Elia Palange, Alessandro Ciattoni. Electromagnetic chirality induced by graphene inclusions in multilayered metamaterials[J]. Photonics Research, 2014, 2(5): 05000121.

Electromagnetic chirality induced by graphene inclusions in multilayered metamaterials Download： 833次

1. INTRODUCTION

2. EFFECTIVE MEDIUM APPROACH

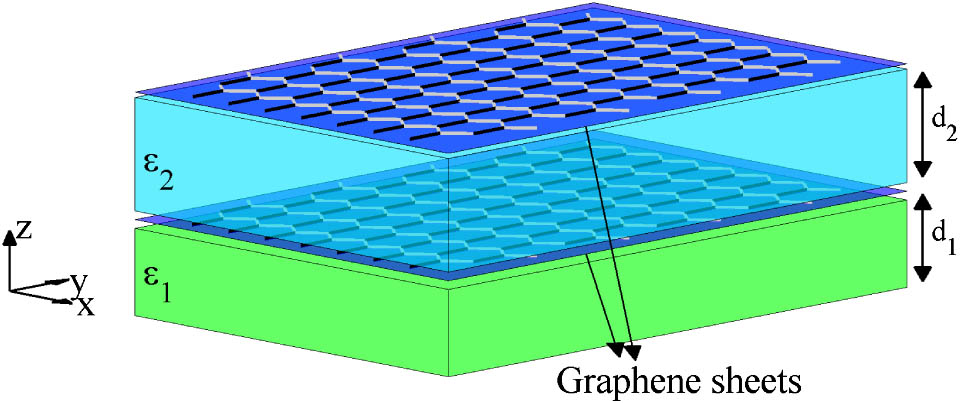
Fig. 1. Sketch of graphene-based metamaterial unit cell. $ϵ_{j}$ and $d_{j}$ ( $j = 1,2$ ) are the relative dielectric permittivities and the thicknesses of the dielectric layers, respectively.

3. SPATIAL DISPERSION AND CHIRALITY

4. GRAPHENE-INDUCED TUNABLE ELECTROMAGNETIC CHIRALITY

Fig. 2. Effective parameters (a) $ϵ_{x}^{(eff)}$ and (b) $τ^{(eff)}$ as functions of the graphene chemical potential $μ_{c}$ .

5. CONCLUSION

Article Outline

关于本站 Cookie 的使用提示

全站搜索

Electromagnetic chirality induced by graphene inclusions in multilayered metamaterials Download： 833次

1. INTRODUCTION

2. EFFECTIVE MEDIUM APPROACH

Fig. 1. Sketch of graphene-based metamaterial unit cell. ϵj and dj (j=1,2) are the relative dielectric permittivities and the thicknesses of the dielectric layers, respectively.

3. SPATIAL DISPERSION AND CHIRALITY

4. GRAPHENE-INDUCED TUNABLE ELECTROMAGNETIC CHIRALITY

Fig. 2. Effective parameters (a) ϵx(eff) and (b) τ(eff) as functions of the graphene chemical potential μc.

5. CONCLUSION

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

Fig. 1. Sketch of graphene-based metamaterial unit cell. $ϵ_{j}$ and $d_{j}$ ( $j = 1,2$ ) are the relative dielectric permittivities and the thicknesses of the dielectric layers, respectively.

Fig. 2. Effective parameters (a) $ϵ_{x}^{(eff)}$ and (b) $τ^{(eff)}$ as functions of the graphene chemical potential $μ_{c}$ .