3D trajectory planning for gliding vehicle using linear pseudospectral model predictive control
0 引 言
滑翔飞行器在再入过程中要经历复杂的环境条件,因此再入制导律的设计至关重要[1]。再入制导方法通常可分为两类:标称轨迹制导和预测校正制导。经典的标称轨迹制导算法为航天飞机再入制导律[2],Shen和Lu利用拟平衡滑翔假设将路径约束简化为倾侧角约束,完成了三维再入轨迹在线快速规划[3],随后为了改进侧向制导的精度,Shen采用横程参数替代航天飞机制导算法的航向瞄准误差,提出了新的倾侧角反转判定方法[4]。尽管标称轨迹制导算法得到广泛应用,但是该类算法太依赖于参考轨迹的设计,为了提高再入制导算法的灵活性和鲁棒性,研究者们转向预测校正制导方法。该算法不依赖预先设计的轨迹,而是通过在线预测终端误差修正控制参数完成任务。
目前的预测校正算法需要利用数值计算的方式求解控制参数的梯度信息,计算效能消耗随控制参数数量成倍增加,因此该类制导算法的控制参数通常很少,这样只能满足部分终端约束。此外,基于航向角误差走廊的传统侧向制导方法,不仅减弱了高升阻比飞行器的横向机动能力,同时横向误差较大,倾侧角反转次数较多。Yu和Chen利用弹道阻尼和谱分解方法,基于解析的在线轨迹规划提出了一种预测制导算法[5],Yang利用线性伪谱方法预测终端误差设计了模型预测制导方法[6]。
前述研究中攻角都是事先规划,没有在线调整能力,终端位置通过倾侧角幅值调整和符号反转完成,横向机动的调节能力还可增强。此外,为了实现一些特殊任务,还需考虑更多的终端约束,例如为了实现特殊的攻击角度,需要考虑特定的航向角约束。因此在Yang提出的线性伪谱再入制导方法的基础上,借鉴如今在导航、制导和控制里得到广泛运用的神经网络技术[7-9],从神经网络泛化的角度出发[10],通过引入高维多项式代理技术,研究将攻角纳入规划控制变量的再入轨迹规划方法。该方法能供快速规划所需要的再入弹道,并通过调整攻角达到对横向机动轨迹进行调整的目的,从而保证能够获得所需的终端航向角约束,开展了多个不同状态的算例测试,得到了满意的仿真结果。
1 再入问题数学模型
1.1 动力学方程
基于圆球模型的质点再入动力学方程为:
$\begin{split} &\dot r = v\sin \gamma {\rm{ ;}}\dot \theta = \dfrac{{v\cos \gamma \sin \psi }}{{r\cos \phi }};\dot \phi = \dfrac{{v\cos \gamma \cos \psi }}{r} \\ & \dot v = - \dfrac{D}{m} - g\sin \gamma + {\omega ^2}r\cos \phi \left( \begin{array}{l} \sin \gamma \cos \phi \\ - \cos \gamma \cos \psi \sin \phi \\ \end{array} \right){\rm{ }} \\ & \dot \gamma = \dfrac{{L\cos \sigma }}{{mv}} - \left( {\dfrac{g}{v} - \dfrac{v}{r}} \right)\cos \gamma + 2\omega \sin \psi \cos \phi + \\ & {\rm{ }}\dfrac{{{\omega ^2}r}}{v}\cos \phi \left( {\cos \gamma \cos \phi + \sin \gamma \cos \psi \sin \phi } \right){\rm{ }} \\ & \dot \psi = \dfrac{{L\sin \sigma }}{{vm\cos \gamma }} + \dfrac{v}{r}\cos \gamma \sin \psi \tan \phi - \\ & {\rm{ }}2\omega \left( {\tan \gamma \cos \psi \cos \phi - \sin \phi } \right) + \\ & {\rm{ }}\dfrac{{{\omega ^2}r}}{{v\cos \gamma }}\sin \psi \sin \phi \cos \phi {\rm{ }} \\ \end{split} $ (1)
式中:
$r = {R_e} + h$,h为飞行器质心高度,
${R_e}$为地球半径,6 378 245 m;θ和ϕ分别为经度和纬度;v为飞行器相对地球的速度值,m/s;γ为航迹角,表示飞行器相对地球的速度与当地水平面的夹角;ψ为航向角,表示飞行器相对地球的速度在当地水平面的投影与正北方向的夹角,顺时针为正;m为飞行器质量,kg;
$g = \mu /{r^2}$表示当地重力加速度,m/s2,μ为地球重力常数;σ为倾侧角,表示飞行器沿速度方向旋转的角度;ω为地球自转角速度,7.292 1×10−5 rad/s;L和D分别表示飞行器受的升力和阻力:
$L = \frac{1}{2}\rho {v^2}{C_l}{S_{ref}};D = \frac{1}{2}\rho {v^2}{C_d}{S_{ref}}$ (2)
$\rho = {\rho _0}\exp \left( { - h/H} \right)$为大气密度,
${\rho _0}$为海平面标准大气压,1.225 kg/m3,H为大气密度常数,7200;Sref为飞行器特征面积;Cl和Cd分别表示飞行器的升力、阻力系数,是关于马赫数和攻角的函数。
1.2 过程约束
路径约束包括热流密度[11-12]、动压和过载约束:
$\begin{array}{l} \dot Q = {K_Q}{\left( \rho \right)^{0.5}}{V^{3.15}} \leqslant {{\dot Q}_{\max }} \\ q = 0.5\rho {V^2} \leqslant {q_{\max }} \\ n = \dfrac{{\sqrt {{L^2} + {D^2}} }}{{m{g_0}}} \leqslant {n_{\max }} \\ \end{array} $ (3)
式中:
$\dot Q$为热流密度;KQ为常数;
$q$为动压;
$n$为过载;
${g_0}$为海平面重力加速度;
${\dot Q_{\max }}$、
${q_{\max }}$和
${n_{\max }}$分别为飞行器能承受的最大热流、动压和过载。
终端状态约束如下,新的航向角约束是为了实现特殊的飞行任务:
$\left\{ \begin{array}{l} h\left( {{E_f}} \right) = {h_f},v\left( {{E_f}} \right) = {v_f},\sigma \left( {{E_f}} \right) = 0 \\ \lambda \left( {{E_f}} \right) = {\lambda _f},\phi \left( {{E_f}} \right) = {\phi _f},\psi \left( {{E_f}} \right) = {\psi _f} \\ \end{array} \right.$ (4)
Ef为终端能量,
$E = - \mu /r + {v^2}/2$;其余以f为下标的状态量为终端状态,终端倾侧角为后面的飞行保留调整余量。
1.3 飞行器模型
以CAV-H作为研究模型,质量为907 kg,特征面积为0.483 9 m2,最大升阻比接近3.5[13]。Cl和Cd用高阶多项式拟合,攻角的调节范围是5 ~ 20°。最大热流、动压和过载分别为500 W/cm2、100 kPa和2。攻角为分段函数:
$\left\{ \begin{array}{l} \alpha = {\alpha _{\rm{b}}},E > {E_{{\rm{mid}}}} \\ \alpha = f\left( E \right)\left( {{\alpha _{\rm{b}}} - {\alpha _f}} \right) + {\alpha _f},{E_f} \leqslant E \leqslant {E_{{\rm{mid}}}} \\ \end{array} \right.$ (5)
$f\left( E \right) = \left( {\frac{{2\left( {E - {E_f}} \right)}}{{\left( {{E_{{\rm{mid}}}} - {E_f}} \right)}} - \frac{{{{\left( {E - {E_f}} \right)}^2}}}{{{{\left( {{E_{{\rm{mid}}}} - {E_f}} \right)}^2}}}} \right)$ (6)
式中:Emid以高度35 km和速度3 500 m/s计算,接近
${E_f}$;
${\alpha _{\rm{b}}}$为控制参数;为了充分发挥攻角的调节能力,
${\alpha _f}$为5°。
1.4 不同攻角下的总升阻比估算与拟合
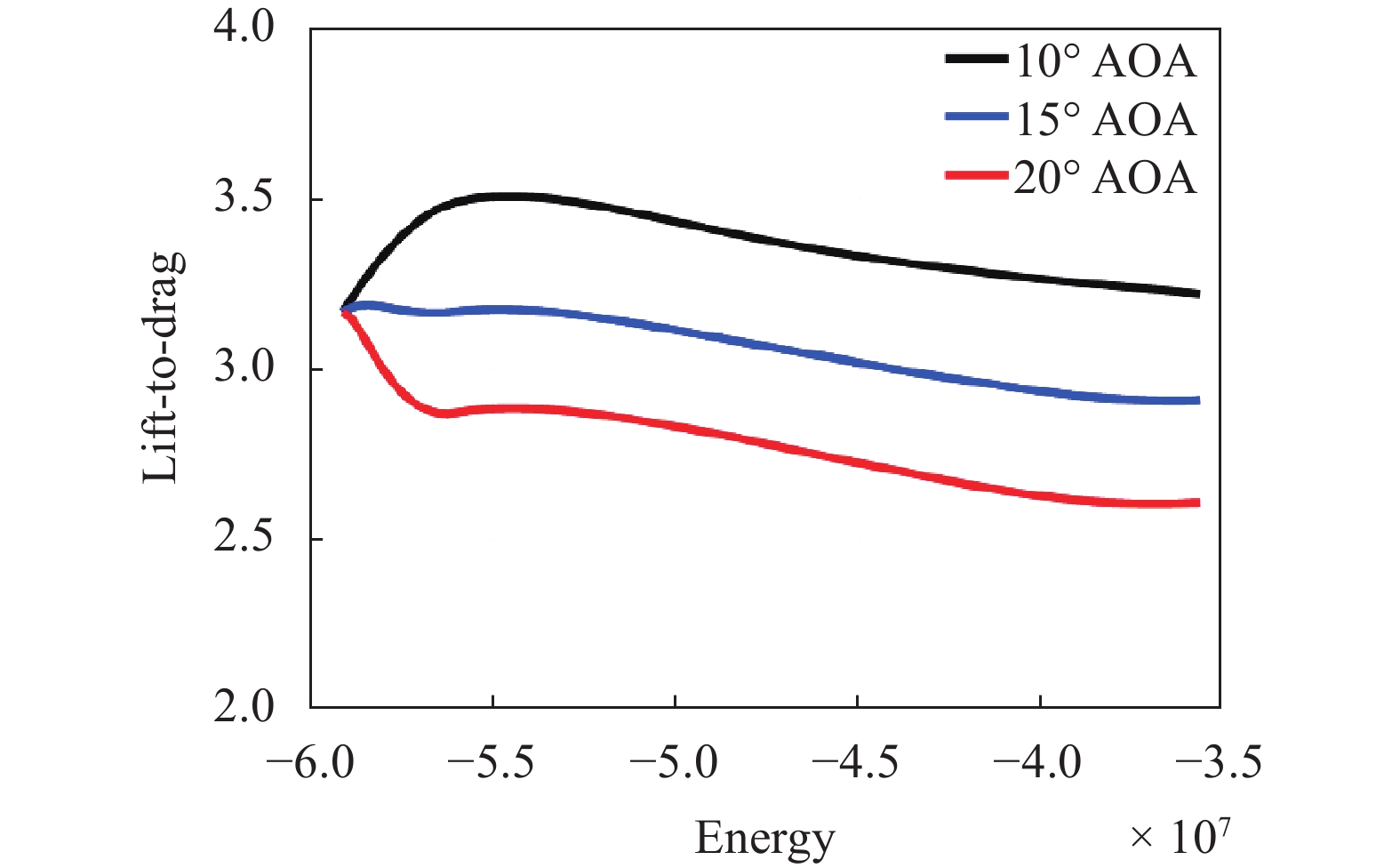
针对不同的常值攻角,结合能量方程和平衡滑翔条件,联立求解可获得高度速度曲线和升阻比能量曲线。
${\sigma _{\rm{0}}} = {30^ \circ }$,倾侧角留有调节余量。
$\left\{ \begin{array}{l} E{\rm{ = }} - \mu {\rm{/}}r + {v^2}/2 \\ 0 = L\cos {\sigma _{\rm{0}}}{\rm{/}}\left( {mv} \right) - \left( {g{\rm{/}}v - v/r} \right) \\ \end{array} \right.$ (7)
分别对攻角在
${10^ \circ }$,
${15^ \circ }$和
${20^ \circ }$的情况进行仿真计算,如图1,图2所示。
图 1. 升阻比曲线
Fig. 1. Lift to drag ratio curves
下载图片 查看所有图片
图 2. 高度速度曲线
Fig. 2. Height-vs-velocity histories
下载图片 查看所有图片
升阻比可表示为以能量E和攻角α为自变量的函数,采用高维多项式拟合获得满足精度的解析函数:
$F\left( {\alpha ,E} \right) = {\left[ {\begin{array}{*{20}{c}} 1 \\ \alpha \\ {{\alpha ^2}} \end{array}} \right]^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}& \cdots &{{p_{16}}} \\ {{p_{21}}}&{{p_{22}}}& \cdots &{{p_{26}}} \\ {{p_{31}}}&{{p_{32}}}& \cdots &{{p_{36}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 \\ \vdots \\ {{E^5}} \end{array}} \end{array}} \right]$ (8)
2 线性伪谱模型预测三维在线轨迹规划
高升阻比飞行器再入飞行分为下降段和滑翔段。每个阶段的制导策略在后文详述。
2.1 下降段
下降段从初始高度开始,到飞行器能够产生足够的升力保持滑翔时结束。此阶段飞行器速度很快,大气密度急速增加,为了限制最大热流,选择最大容许攻角和零倾侧角的控制指令。
${\alpha _{{\rm{cmd}}}} = {\alpha _{\max }};{\sigma _{{\rm{cmd}}}} = 0$ (9)
当
$\dot h = v\sin \gamma = 0$时,下降段结束,滑翔段开始。
2.2 滑翔段
滑翔段以多段线性伪谱法更新倾侧反转点和控制量,引导飞行器飞向交班点,并为后续飞行保留足够的能量。
2.2.1 降阶动力学方程
根据平衡滑翔假设简化动力学方程得到如下方程,航向角方程中第一项的符号随倾侧角反转而改变。记
${{x}} = {\left[ {\theta ,\phi ,\varphi } \right]^{\rm{T}}}$,
$\dot {{x}} = {{f}}$,根据符号的变化可将降阶动力学方程分为三段,分别记作
${{{f}}_1}$,
${{{f}}_2}$和
${{{f}}_3}$。
$\left\{ \begin{array}{l} \dfrac{{\rm{d}\theta }}{{{\rm{d}}E}}{\rm{ = }} - \dfrac{{\sin \psi }}{{{\varTheta }\left( {E,\psi ,\phi } \right)r\cos \phi }}F\left( {\alpha ,E} \right)u;{\rm{ }} \\ \dfrac{{\rm{d}\phi }}{{{\rm{d}}E}}{\rm{ = }} - \dfrac{{\cos \psi }}{{{\varTheta }\left( {E,\psi ,\phi } \right)r}}F\left( {\alpha ,E} \right)u; \\ \dfrac{{\rm{d}\psi }}{{{\rm{d}}E}}{\rm{ = }} \mp \dfrac{1}{{2\left( {E + \mu /r} \right)}}F\left( {\alpha ,E} \right)\sqrt {1 - {u^2}} - \\ \left( \begin{array}{l} \dfrac{{\sin \psi \tan \phi }}{{{\varTheta }\left( {E,\psi ,\phi } \right)r}}{\rm{ + }}\dfrac{{2{\omega _e}\sin \phi }}{{{\varTheta }\left( {E,\psi ,\phi } \right)\sqrt {2\left( {E + \mu /r} \right)} }}{\rm{ + }} \\ \dfrac{{\omega _e^2r\sin \psi \sin \phi \cos \phi }}{{2\left( {E + \mu /r} \right){\varTheta }\left( {E,\psi ,\phi } \right)}} \\ \end{array} \right)F\left( {\alpha ,E} \right)u \\ \end{array} \right.$ (10)
$\begin{split} {\varTheta }\left( {E,\psi ,\phi } \right) =& - \left( {\dfrac{{2E}}{r} + \frac{\mu }{{{r^2}}}} \right) - \omega _e^2r{\cos ^2}\phi - \\ &2\sqrt {2\left( {E + \dfrac{\mu }{r}} \right)} {\omega _e}\sin \psi \cos \phi \\ \end{split} $ (11)
其中
$u = \cos \sigma $,升阻比为F,
$h$的取值为当前高度与
${h_f}$的平均值。
${\varTheta }$关于
$\phi $、
$\psi $的偏导数如下:
$\begin{array}{l} \dfrac{{\rm{d}{\varTheta }}}{{\rm{d}\phi }} = 2\sqrt {2\left( {E + \dfrac{\mu }{r}} \right)} {\omega _e}\sin \psi \sin \phi + 2\omega _e^2r\sin \phi \cos \phi \\ \dfrac{{\rm{d}{\varTheta }}}{{\rm{d}\psi }} = - 2\sqrt {2\left( {E + \dfrac{\mu }{r}} \right)} {\omega _e}\cos \psi \cos \phi \\ \end{array} $ (12)
2.2.2 控制参数化
为了既能消除终端误差又能保持较大的横向机动能力,设置两个倾侧反转点Ere1和Ere2。先令
${E_{re2}} = {E_{mid}}$,计算Ere1;第一次反转完成后,再计算Ere2。
$u$用分段函数来表征:
$\left\{ \begin{array}{l} u = {u_{\rm{b}}},E > {E_{{\rm{mid}}}} \\ u = f\left( E \right)\left( {{u_{\rm{b}}} - 1} \right) + 1,{E_f} \leqslant E \leqslant {E_{{\rm{mid}}}} \\ \end{array} \right.$ (13)
因此全段的控制就可以用参数
${u_{\rm{b}}}$,
${\alpha _{\rm{b}}}$,
${E_{re{\rm{1}}}}$和
${E_{re2}}$来表征。
2.2.3 线化动力学方程
对于降阶动力学系统,给定初始控制参数,可以通过数值积分预测飞行轨迹,从而得到相对终端状态约束的偏差
$\delta {x_f} = x({E_f}) - {x_f}$。将降阶动力学方程在标称轨迹附近泰勒展开,忽略高阶项,令
${U_{\rm{b}}} = {\left[ {{u_{\rm{b}}},{\alpha _{\rm{b}}}} \right]^{\rm{T}}}$得到以状态偏差为自变量的线性动力学方程如下:
$\left\{ \begin{array}{l} \delta {\dot{ x}} = {{{A}}_1}\left( E \right)\delta {{x}} + {{{B}}_1}\left( E \right)\delta {U_{\rm{b}}},E > {E_{re1}} \\ \delta {\dot{ x}} = {{{A}}_2}\left( E \right)\delta {{x}} + {{{B}}_2}\left( E \right)\delta {U_{\rm{b}}},{E_{re2}} \leqslant E \leqslant {E_{re1}} \\ \delta {\dot{ x}} = {{{A}}_3}\left( E \right)\delta {{x}} + {{{B}}_3}\left( E \right)\delta {U_{\rm{b}}},{E_f} \leqslant E \leqslant {E_{re2}} \\ \end{array} \right.$ (14)
其中
${{x}} = {{{x}}_{ref}} - \delta {{x}}$,
${U_{\rm{b}}} = {U_{ref}} - \delta {U_{\rm{b}}}$。
${{{B}}_i}\left( E \right) = \left\{ \begin{array}{l} {{B}}\left( E \right),E > {E_{{\rm{mid}}}}\\ {{B}}\left( E \right)f\left( E \right)\left( {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right),\;{E_f} \le E \le {E_{{\rm{mid}}}} \end{array} \right.$ (15)
${{{A}}_i}\left( E \right)$是一个3×3的矩阵,
${{B}}\left( E \right)$是一个3×2的矩阵。与参考文献[6]中系数不同,此处的系数考虑了攻角变化,
${{{A}}_i}\left( E \right)$和
${{B}}\left( E \right)$的表达式表示为:
${{{A}}_i}\left( E \right) = \left[ {\begin{array}{*{20}{c}} 0&{{a_{12}}}&{{a_{13}}}\\ 0&{{a_{22}}}&{{a_{23}}}\\ 0&{{a_{32}}}&{{a_{33}}} \end{array}} \right],\;{{B}}\left( E \right) = \left[ {\begin{array}{*{20}{c}} {{b_{{\rm{1}}1}}}&{{b_{{\rm{12}}}}}\\ {{b_{2{\rm{1}}}}}&{{b_{{\rm{22}}}}}\\ {{b_{3{\rm{1}}}}}&{{b_{3{\rm{2}}}}} \end{array}} \right]$ (16)
${a_{12}} = \dfrac{{\sin \psi }}{r}\left( {\dfrac{{\partial {\varTheta }}}{{\partial \phi }}/\left( {{{\varTheta }^2}\cos \phi } \right) - \dfrac{{\sin \phi }}{{{\varTheta }{{\cos }^2}\phi }}} \right)F\left( \alpha \right)u$ (17)
${a_{13}} = - \dfrac{1}{{r\cos \phi }}\left( {\dfrac{{\cos \psi }}{{\varTheta }} - \dfrac{{\partial {\varTheta } }}{{\partial \psi }}\dfrac{{\sin \psi }}{{{{\varTheta } ^2}}}} \right)F\left( \alpha \right)u$ (18)
${b_{{\rm{1}}1}} = - \dfrac{{\sin \psi }}{{{\varTheta }r\cos \phi }}F\left( \alpha \right)$ (19)
${b_{{\rm{12}}}} = - \frac{{\sin \psi }}{{{\varTheta } r\cos \phi }}\frac{{\partial F}}{{\partial \alpha }}u$ (20)
${a_{22}} = \frac{{\cos \psi }}{{r{{\varTheta }^2}}}\frac{{\partial {\varTheta } }}{{\partial \phi }}F\left( \alpha \right)u$ (21)
${a_{23}} = \dfrac{1}{r}\left( {\dfrac{{\sin \psi }}{{\varTheta }} + \dfrac{{\cos \psi }}{{{{\varTheta }^2}}}\dfrac{{\partial {\varTheta } }}{{\partial \psi }}} \right)F\left( \alpha \right)u$ (22)
${b_{2{\rm{1}}}} = - \dfrac{{\cos \psi }}{{{\varTheta }r}}F\left( \alpha \right)$ (23)
${b_{2{\rm{2}}}} = - \dfrac{{\cos \psi }}{{{\varTheta }r}}\frac{{\partial F}}{{\partial \alpha }}u$ (24)
${a_{32}} = \left( \begin{array}{l} \left( \begin{array}{l} \dfrac{{\sin \psi }}{{r\cos \phi }} + \dfrac{{2{\omega _e}}}{{\sqrt {2\left( {E + \mu {\rm{/}}r} \right)} }} + \\ \dfrac{1}{2}\dfrac{{\omega _e^2r\sin \psi \cos \phi }}{{\left( {E + \mu {\rm{/}}r} \right)}} \end{array} \right)\dfrac{{\sin \phi }}{{{{\varTheta } ^2}}}\dfrac{{\partial {\varTheta }}}{{\partial \phi }}\\ - \left( \begin{array}{l} \dfrac{{\sin \psi }}{{r{{\cos }^2}\phi }}{\rm{ + }}\dfrac{{2{\omega _e}\cos \phi }}{{\sqrt {2\left( {E + \mu {\rm{/}}r} \right)} }}、{\rm{ + }}\\ \dfrac{1}{2}\dfrac{{\omega _e^2r\sin \psi \cos 2\phi }}{{\left( {E + \mu {\rm{/}}r} \right)}} \end{array} \right)\dfrac{1}{{\varTheta }} \end{array} \right)F\left( \alpha \right)u$ (25)
${a_{33}} = \left( \begin{array}{l} \left( \begin{array}{l} \dfrac{{\sin \psi }}{{\cos \phi r}} + \dfrac{{2{\omega _e}}}{{\sqrt {{\rm{2}}\left( {E + \mu {\rm{/}}r} \right)} }} \\ \dfrac{{\omega _e^2r\cos \phi \sin \psi }}{{2\left( {E + \mu {\rm{/}}r} \right)}} \\ \end{array} \right)\dfrac{{\sin \phi }}{{{{\varTheta } ^2}}}\dfrac{{\partial {\varTheta }}}{{\partial \psi }} \\ - \left( {\dfrac{1}{{r\cos \phi }} + \dfrac{{\omega _e^2r\cos \phi }}{{2\left( {E + \mu {\rm{/}}r} \right)}}} \right)\dfrac{{\sin \phi \cos \psi }}{{\varTheta } } \\ \end{array} \right)F\left( \alpha \right)u$ (26)
$\begin{array}{l} {b_{3{\rm{1}}}} = \pm \dfrac{{F\left( \alpha \right)u}}{{2\left( {E + \mu /r} \right)\sqrt {{\rm{1}} - {u^2}} }} - \\ {\rm{ }}\left( \begin{array}{l} \dfrac{{\sin \psi \tan \phi }}{{{\varTheta }r}}{\rm{ + }}\dfrac{{2{\omega _e}\sin \phi }}{{{\varTheta }\sqrt {2\left( {E + \mu {\rm{/}}r} \right)} }} \\ {\rm{ + }}\dfrac{{\omega _e^2r\sin \psi \sin \phi \cos \phi }}{{2\left( {E + \mu /r} \right){\varTheta }}} \\ \end{array} \right)F\left( \alpha \right) \\ \end{array} $ (27)
$\begin{array}{l} {b_{3{\rm{2}}}} = \mp \dfrac{{\sqrt {1 - {u^2}} }}{{2\left( {E + \mu /r} \right)}}\dfrac{{\partial F}}{{\partial \alpha }}\sqrt {{\rm{1}} - {u^2}} -\\ \left( \begin{array}{l} \dfrac{{\sin \psi \tan \phi }}{{{\varTheta }r}}{\rm{ + }}\dfrac{{2{\omega _e}\sin \phi }}{{{\varTheta }\sqrt {2\left( {E + \mu {\rm{/}}r} \right)} }} \\ {\rm{ + }}\dfrac{{\omega _e^2r\sin \psi \sin \phi \cos \phi }}{{2\left( {E + \mu /r} \right){\varTheta }}} \\ \end{array} \right)\dfrac{{\partial F}}{{\partial \alpha }}u \\ \end{array} $ (28)
2.2.4 多段线性伪谱模型预测控制
终端状态可以表示为控制参数的函数:
$\begin{array}{l} {{x}}\left( {{E_f}} \right) = {{g}}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right) = {{{x}}_0} + \\ \displaystyle\int_{{E_0}}^{{E_{re1}}} {{{{f}}_1}\left( {{{x}},{U_{\rm{b}}}} \right){\rm{d}}E + } \int_{{E_{re1}}}^{{E_{re2}}} {{{{f}}_2}\left( {{{x}},{U_{\rm{b}}}} \right){\rm{d}}E + } \int_{{E_{re2}}}^{{E_f}} {{{{f}}_3}\left( {{{x}},{U_{\rm{b}}}} \right){\rm{d}}E} \\ \end{array} $ (29)
令
$\delta U = {\left[ {\delta {U_{\rm{b}}},\delta {E_{re1}},\delta {E_{re2}}} \right]^{\rm{T}}}$,假设
$\delta U$为小量,将终端状态在标称轨迹附近泰勒展开并忽略高阶项可得:
$\delta {{{x}}_f} = \frac{{\partial {{g}}}}{{\partial U}}\delta U$ (30)
$\dfrac{{\partial {{g}}}}{{\partial U}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {g_\theta }}}{{\partial {u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\theta }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\theta }}}{{\partial {E_{re1}}}}}&{\dfrac{{\partial {g_\theta }}}{{\partial {E_{re2}}}}} \\ {\dfrac {\partial {g_\phi }}{{\partial{u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\phi }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\phi }}}{{\partial {E_{re1}}}}}&{\dfrac{{\partial {g_\phi }}}{{\partial {E_{re2}}}}} \\ {\dfrac{{\partial {g_\psi }}}{{\partial {u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\psi }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\psi }}}{{\partial {E_{re1}}}}}&{\dfrac{{\partial {g_\psi }}}{{\partial {E_{re2}}}}} \end{array}} \right]$ (31)
$\delta U = {\left( {\frac{{\partial {{g}}}}{{\partial U}}} \right)^{ - 1}}\delta {{{x}}_f}$ (32)
根据公式(29)直接计算控制量的修正值需要积分运算,很难得到解析解。用拉格朗日插值多项式来拟合状态量和控制量,可将微分动力学方程转化为一组线性代数方程,从而简化计算过程[6]。结合偏差微分方程(14)与高斯伪谱法得到终端偏差的表达式为:
$\begin{split} \delta {{{x}}_f} =& {{K}}_3^x{{K}}_2^x{{K}}_1^x\delta {x_0} + {{K}}_3^x{{K}}_2^x\delta {{{x}}_{re1}} + {{K}}_3^x\delta {{{x}}_{re2}}+\\ & \left( {{{K}}_3^x{{K}}_2^x{{K}}_1^u + {{K}}_3^x{{K}}_2^u + {{K}}_3^u} \right)\delta {U_{\rm{b}}} \\ \end{split} $ (33)
$\delta {{{x}}_0}$为初始状态偏差,轨迹规划从当前状态开始,因此
$\delta {{{x}}_0} = 0$。关于控制参量的偏导数为:
${\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {{g}}}}{{\partial {u_{\rm{b}}}}}}&{\dfrac{{\partial {{g}}}}{{\partial {\alpha _{\rm{b}}}}}} \end{array}} \right]^{\rm{T}}} = {{K}}_3^x{{K}}_2^x{{K}}_1^u + {{K}}_3^x{{K}}_2^u + {{K}}_3^u$ (34)
$\delta {E_{re1}}$和
$\delta {E_{re2}}$分别引起
${E_{re1}}$和
${E_{re2}}$时刻的状态偏差
$\delta {{{x}}_{re1}}$和
$\delta {{{x}}_{re2}}$,结合公式(29)由变分法得到:
$\delta {{{x}}_{re1}} = \left[ {{{{f}}_1}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right.\left. { - {{{f}}_2}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right]\delta {E_{re1}}$ (35)
$\delta {{{x}}_{re2}} = \left[ {{{{f}}_2}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right.\left. { - {{{f}}_3}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right]\delta {E_{re2}}$ (36)
$\frac{{\partial {{g}}}}{{\partial {E_{re1}}}} = {{K}}_3^x{{K}}_2^x\left[ {{{{f}}_1}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right.\left. { - {{{f}}_2}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right]$ (37)
$\frac{{\partial {{g}}}}{{\partial {E_{re2}}}} = {{K}}_3^x\left[ {{{{f}}_2}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right.\left. { - {{{f}}_3}\left( {{U_{\rm{b}}},{E_{re1}},{E_{re2}}} \right)} \right]$ (38)
$\begin{array}{l} {{K}}_i^x = \left\{ {{{1}} - {\rm{d}}{E_i}{{{1}}^{\rm{T}}}{{{A}}_i}{{{W}}_i}{{\left[ {{{{D}}_{2:n}} - {\rm{d}}{E_i}{{{A}}_i}} \right]}^{ - 1}}{{{D}}_1}} \right\} \\ {{K}}_i^u = \left\{ \begin{array}{l} {\rm{d}}{E_i}^2{{{1}}^{\rm{T}}}{{{A}}_i}{{{W}}_i}{\left[ {{{{D}}_{2:n}} - {\rm{d}}{E_i}{{{A}}_i}} \right]^{ - 1}}{{{B}}_i} \\ + {\rm{d}}{E_i}{{B}}_i^{\rm{T}}{{{W}}_i}{{1}} \\ \end{array} \right\} \\ \end{array} $ (39)
${{{A}}_i} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_i}\left( {{E_1}} \right)}& \cdots &0 \\ \vdots & \ddots & \vdots \\ 0& \cdots &{{{{A}}_i}\left( {{E_n}} \right)} \end{array}} \right],{{{B}}_i} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_i}\left( {{E_1}} \right)} \\ \vdots \\ {{{{B}}_i}\left( {{E_n}} \right)} \end{array}} \right]$ (40)
${E_{i{\rm{ - 1}}}}$与
${E_i}$为该段初始与终端能量,
${\rm{d}}{E_i}{\rm{ = }}\left( {{E_i} - {E_{i - 1}}} \right)/2$,
${E_1}$~
${E_n}$为配点处能量,
${{{W}}_i}$为高斯积分权重矩阵,
${{{D}}_1},{{{D}}_{2:n}}$为高斯微分近似矩阵。控制修正量为:
$\left[ {\begin{array}{*{20}{c}} {\delta {u_{\rm{b}}}} \\ {\delta {\alpha _{\rm{b}}}} \\ {\delta {E_{rei}}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {g_\theta }}}{{\delta {u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\theta }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\theta }}}{{\partial {E_{rei}}}}} \\ {\dfrac{{\partial {g_\phi }}}{{\delta {u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\phi }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\phi }}}{{\partial {E_{rei}}}}} \\ {\dfrac{{\partial {g_\psi }}}{{\delta {u_{\rm{b}}}}}}&{\dfrac{{\partial {g_\psi }}}{{\partial {\alpha _{\rm{b}}}}}}&{\dfrac{{\partial {g_\psi }}}{{\partial {E_{rei}}}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\delta {\theta _f}} \\ {\delta {\psi _f}} \end{array}} \right]$ (41)
其中i=1,2,迭代更新控制参数直至满足终端约束,调节
${E_{re1}}$时,
${E_{re2}} = {E_{{\rm{mid}}}}$。
2.2.5 过程约束管理策略
路径约束可以转化为对倾侧角大小的约束:
$\begin{array}{l} \sigma \left( v \right) \leqslant {\sigma _{\max }}\left( v \right) = \\ \arccos \left( {\dfrac{{m\left( {g\left( {{r_{\min }}} \right) - {v^2}{\rm{/}}{r_{\min }}} \right)}}{{{k_L}L\left( {{r_{\min }}} \right)}} + {k_{cst}}\left( {\dfrac{{{\rm{d}}r}}{{{\rm{d}}v}} - {{\left. {\dfrac{{{\rm{d}}r}}{{{\rm{d}}v}}} \right|}_{\dot Q,q,n}}} \right)} \right) \\ \end{array} $ (42)
式中:
${r_{\min }}$为给定速度下满足约束的最小高度;
${k_L} = \tilde L/L$,
$L$为根据模型计算出的升力,
$\tilde L$为测量得到的升力;
${\rm{d}}r/{\rm{d}}v$和
$\left. {\left( {{\rm{d}}r/{\rm{d}}v} \right)} \right|\dot Q,q,n$分别为再入动力学和过程约束方程中高度对速度的导数;kcst是一个常数,当存在约束没有满足时大于零,其余情况下等于零[6]。
3 仿真结果
新的轨迹规划方法考虑了包含地球自转项在内的多种非线性项,通过将攻角引入规划变量,极大地增强了飞行器的调节能力,下面结合不同的初始和终端条件,开展仿真验证。初始状态为:高度55 km,速度 7 000 m/s;终端约束为:高度30 km,速度2 500 m/s,初始航向角、终端位置和航向角根据任务需求具体确定,其具体取值参考表1。
表 1.
Initial and terminal states
初始终端状态
Table 1.
Initial and terminal states
初始终端状态
| Case | Initial heading angle/(°) | Terminal heading angle/(°) | Terminal longitude/(°) | Terminal latitude/(°) | | 1 | 90 | 65 | 120 | 0 | | 2 | 90 | 70 | 120 | 0 | | 3 | 90 | 75 | 120 | 0 | | 4 | 110 | 135 | 110 | 0 | | 5 | 110 | 130 | 110 | 0 | | 6 | 110 | 125 | 110 | 0 |
|
查看所有表
值得注意的是CASE-1,2,3选择初始倾侧角符号为1,而CASE-4,5,6,选择初始倾侧角符号为−1。所有算例的计算时间均小于0.1 s,运行环境为频率3.3 GHz、内存16 G计算机下的MATLAB2016b。图3为地面轨迹曲线,两类算例具有不同的初始航向角和飞行方向,但均满足终端位置要求,飞行路径具有较大的横向机动轨迹,通过调节攻角能够对横向轨迹进行一定的调整。图4为航向角曲线,两类算例的初始航向角相同,经过两次倾侧反转都满足所需要的终端航向角,从航向角曲线也能清晰的看出各算例具有不同的倾侧反转时刻。
图 4. 航向角曲线
Fig. 4. Heading angle histories
下载图片 查看所有图片
计算所获得控制变量如表2所示,攻角都在5 ~ 20°内变化,且根据终端航向角的需求不同,将攻角的调节能力完全发挥出来,航向角和第一次反转时刻也都确定。
表 2.
Control variables
控制变量
Table 2.
Control variables
控制变量
| Case | Angle of attack/(°) | Bank angle/(°) | Reversal energy | | 1 | 9.091 | 0.6514 | −4.559 5E7 | | 2 | 13.53 | 0.7008 | −4.564 6E7 | | 3 | 18.55 | 0.7661 | −4.572 3E7 | | 4 | 11.82 | 0.6876 | −4.258 8E7 | | 5 | 15.81 | 0.7970 | −4.223 8E7 | | 6 | 20.64 | 0.7661 | −4.170 40E7 |
|
查看所有表
终端误差如表3所示,可见该算法具有很高的计算精度。综合而言,所提出的方法将攻角纳入控制量,能有效的调节横向机动轨迹,在保证终端位置的条件下,有效调节终端航向角。
表 3.
Terminal error
终端误差
Table 3.
Terminal error
终端误差
| Case | Longitude/(°) | Latitude/(°) | Heading angle/(°) | | CASE-1 | 2.92E-10 | 1.53E-6 | 2.42E-10 | | CASE-2 | 2.07E-10 | 2.70E-7 | 3.39E-10 | | CASE-3 | 7.37E-11 | 7.00E-7 | 5.48E-11 | | CASE-4 | 4.31E-10 | 1.07E-7 | 1.29E-10 | | CASE-5 | 8.99E-9 | 4.21E-8 | 1.63E-10 | | CASE-6 | 5.39E-9 | 6.65E-7 | 5.43E-7 |
|
查看所有表
4 结 论
为了满足特定的终端航向角约束,基于线性伪谱模型预测控制技术研究了将攻角纳入控制变量的三维再入轨迹规划算法。该方法首先采用高维多项式代理技术,并结合拟平衡滑翔条件泛化升阻比,获得升阻比关于攻角和能量的泛化函数。随后对再入动力学方程进行降阶处理,保留地球自转等非线性影响因素,并对降阶后的动力学方程进行线性化处理获得误差传播方程,推导了在伪谱离散条件下关于终端位置和航向角偏差的攻角、倾侧角和倾侧角时刻解析修正关系,最终实现轨迹的在线解算。同时由于攻角参与调节,极大增强了再入轨迹的横向机动调整能力。几类典型算的仿真结果表明:该方法不仅能够保证终端和航向角,还具有很快的求解速度和很高的计算精度,适合在线应用。
孙建波, 潘幸华, 杨良, 陈万春, 赵育善. 滑翔飞行器线性伪谱模型预测控制三维轨迹规划[J]. 红外与激光工程, 2020, 49(9): 20200279. Jianbo Sun, Xinghua Pan, Liang Yang, Wanchun Chen, Yushan Zhao. 3D trajectory planning for gliding vehicle using linear pseudospectral model predictive control[J]. Infrared and Laser Engineering, 2020, 49(9): 20200279.
 下载: 615次
下载: 615次