Zeta电位计算过程中Henry函数的优化表达式

秦福元; 刘伟; 王文静; JohnC.Thomas; 王雅静; 申晋

doi:doi:10.3788/AOS201737.1029003

光学学报, 2017, 37 (10): 1029003, 网络出版: 2018-09-07

Zeta电位计算过程中Henry函数的优化表达式下载： 837次

An Optimal Expression for Henry Function for the Calculation of Zeta Potential

论文大纲

秦福元 ¹刘伟 ^1,*王文静 ¹JohnC.Thomas ^1,2王雅静 ¹申晋 ¹

作者单位

¹ 山东理工大学电气与电子工程学院, 山东淄博, 255049

² Group Scientific Pty Ltd., 南澳大利亚州, 葛兰许 5022

散射 Henry函数最小二乘法 Zeta电位双电层 scattering Henry function least squares algorithm Zeta potential electric double layer

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

利用电泳光散射法可以确定带电颗粒的电泳迁移率,由电泳迁移率计算颗粒的Zeta电位需要准确确定Henry函数的数值。为此,利用最小二乘算法对精确Henry函数值进行拟合,获得优化Henry函数表达式;基于Gouy-Chapman-Stern双电层模型理论,求解不同浓度、不同类型电解质溶液中颗粒的双电层厚度,从而获得准确的颗粒半径a与双电层厚度k ^-¹的比值ka;最后利用优化的函数表达式获得准确的Henry函数值。使用该方法分别计算4种不同浓度电解质下颗粒的Zeta电位,实验结果表明,利用优化的Henry函数可以有效提高颗粒Zeta电位的计算精度,计算结果的相对误差小于1.0%。

Abstract

The electrophoretic mobility of a charged particle can be determined using the electrophoretic light scattering method. To accurately determine the particle's Zeta potential from the mobility requires the use of Henry function. An optimal expression for Henry function can be fitted by using the least squares algorithm. The thickness of the electric double layer in different concentrations and different types of electrolyte can be calculated using the Gouy-Chapman-Stern double layer model. An accurate value of ka is obtained, here k -1 is the thickness of the double layer and a is the particle radius. The value of ka can be used in the optimal expression to determine an accurate value of Henry function. The particle's Zeta potentials for four different concentrations are measured using this approach. The experimental results show that the optimal Henry function can be used to improve the calculation precision of particle's Zeta potential, and the relative error of the calculation results is less than 1.0%.

1 引言

分散在液体中的颗粒做电泳运动时,固定吸附层和部分溶剂分子会随之一起移动,与液体之间形成滑动面,定义滑动面与液体内部的电位差为Zeta电位^[1]。Zeta电位是衡量胶体稳定性的重要参数,其绝对值越高,表明颗粒间的静电排斥力越大,胶体越稳定;反之,胶体越不稳定。因此,Zeta电位的测量对确定和调节胶体系统的稳定性具有重要意义。但滑动面是一个假想面,Zeta电位无法直接测量,使用电泳光散射的方法,可以测量出带电颗粒在电场中的电泳速度,进而计算出其电泳迁移率^[2]。研究表明,颗粒的Zeta电位与其电泳迁移率间存在着正比例关系,比例系数为Henry函数,只有确定了Henry函数的数值,才可以计算出确切的颗粒Zeta电位,因此,准确确定Henry函数对测量Zeta电位极其重要。

1921年,von Smoluchowski^[3]考虑了电渗,假设电场均匀且平行于颗粒表面,双电层厚度远远小于颗粒的半径,即ka≫1,得出近似比例系数为1.5。1924年,Hückel^[4]针对双电层厚度远远大于颗粒半径的情况,即ka≪1,得出近似比例系数为1.0。1931年,Henry^[5]发现并解决了颗粒使电场变形的问题,分别建立了ka<1和ka>1两种情况下的Henry函数。但是,Henry没有考虑颗粒周围电场变形失真导致的弛豫效应,因此,当ka≈1时,比例系数的相对误差高达100%。1950年,Overbeek^[6]考虑到ka≈1时,电场力、摩擦阻力、电泳阻滞和弛豫效应大小相等,对Henry函数做出了改进,并分别得出了对称和非对称电解质电泳迁移率与Zeta电位的关系式。结果显示,当Zeta电位较高或0.2<ka<50时,改进Henry函数的近似结果都过度补偿了弛豫效应。1966年,Wiersema等^[7]解决了Overbeek近似微分方程造成弛豫效应过度补偿的问题,得到了更加精确的比例系数,但是其处理过程过于复杂冗长。1978年,O'Brien等^[8]基于Wiersema理论,考虑了颗粒之间力的平衡关系,推导出一系列耦合非线性偏微分方程。1983年,Ohshima等^[9]根据O'Brien和White理论,推导出了一个半经验公式,在ka>10时,其相对误差不大于3%。

本文利用最小二乘算法对精确Henry函数值进行拟合,获得优化Henry函数表达式,并在Gouy-Chapman-Stern双电层模型^[10]的基础上,给出双电层厚度的计算方法,从而获得准确的ka值,以便求解Henry函数,从而使所计算的颗粒Zeta电位更精确。

2 Henry函数的优化近似表达式

电泳光散射方法测量颗粒的电泳速度后,电泳迁移率可以通过电泳速度计算出来,而Zeta电位的计算与双电层模型有关,选择的双电层模型不同,计算得到的Zeta电位就不同。应用Gouy-Chapman-Stern双电层模型进行分析,对于刚性球体颗粒,其电泳迁移率与Zeta电位的关系可表示为

\begin{matrix} μ = \frac{2 ε_{r} ε_{0} ζ}{3 η} f (ka), (1) \end{matrix}

式中ζ为颗粒的Zeta电位,μ为颗粒电泳迁移率,ε₀为真空介电常数,ε_r为电解质溶液相对介电常数,η为电解质溶液黏度,f(ka)为Henry函数,ka表示颗粒半径a与双电层厚度k^-1之比。

带电颗粒在电场力作用下运动,同时,作用在颗粒上的液体黏滞力阻止颗粒运动;颗粒表面双电层中的反离子向着电场力反方向移动,产生电泳阻滞力;电场导致颗粒周围离子氛中心落后于颗粒中心,产生的弛豫效应进一步阻止颗粒的运动^[11]。当这4个力处于平衡状态时,颗粒在液体中以恒定速度运动。但是,电泳阻滞力和弛豫效应对双电层厚度的影响难以准确确定,也导致Henry函数无法准确确定。

Henry^[5]根据颗粒使电场变形的条件,给出了Henry函数的分段表达式

\begin{matrix} \begin{matrix} f (ka) = 1 + \frac{{(ka)}^{2}}{16} - \frac{5 {(ka)}^{3}}{48} - \frac{{(ka)}^{4}}{96} + \frac{{(ka)}^{5}}{96} - [\frac{{(ka)}^{4}}{8} - \frac{{(ka)}^{6}}{96}] \exp (ka) E_{n} (ka), ka < 1, \end{matrix} (2) \end{matrix}

式中E_n(ka)是n阶积分形式,E_n(ka)=(ka)^n-¹ $\begin{matrix} \int_{ka}^{\infty} \end{matrix} \begin{matrix} \frac{\exp (- t)}{t^{n}} \end{matrix}$ dt=a^n-¹ $\begin{matrix} \int_{a}^{\infty} \end{matrix} \begin{matrix} \frac{\exp (- ka)}{a^{n}} \end{matrix}$ da。

当ka→0时,f(ka)=1,即Hückel近似,此时μ=2ε_rε₀ζ/3η。

\begin{matrix} f (ka) = \frac{3}{2} - \frac{9}{2 ka} + \frac{75}{2 {(ka)}^{2}} - \frac{330}{{(ka)}^{3}} + \dots, ka > 1 。 (3) \end{matrix}

当ka→¥时,f(ka)=1.5,即Smoluchowski近似,此时μ=ε_rε₀ζ/η。

一般情况下,被测颗粒的ka≫1,故通常采用Smoluchowski近似;当颗粒半径及浓度都很小时,才会出现ka≪1的情况,故Hückel近似应用较少,但适用于非极性溶液中颗粒Zeta电位的测量;当1<ka<20时,上述两个分段表达式所求得的f(ka)值误差较大,Henry函数不再适用。

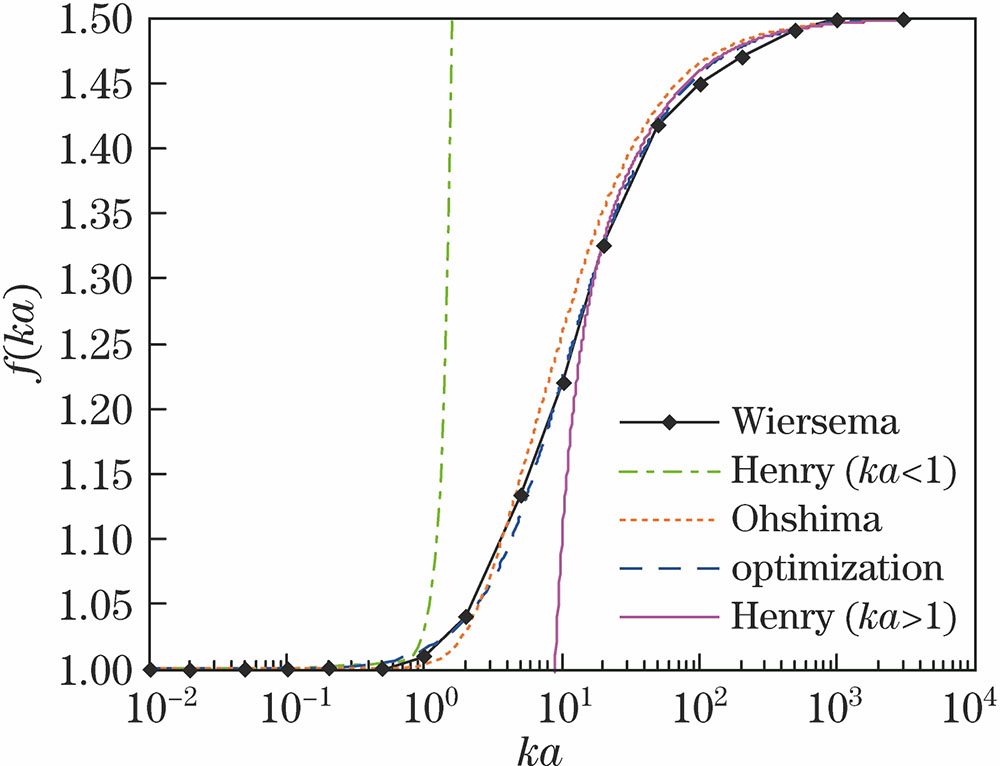
为了解决这一问题,Wiersema等^[7]根据Gouy-Chapman-Stern双电层模型以及颗粒在溶液中的受力情况,推导了颗粒电泳迁移率和Zeta电位的精确微分方程,得到精确的Henry函数值

\begin{matrix} f (ka) = \frac{E}{y}, (4) \end{matrix}

式中E=3ηeμ/(2ε₀ε_rk_BT),y=eζ/(k_BT),k_B为玻尔兹曼常数,T为绝对温度,e表示元电荷。Wiersema等式计算过程极为复杂,为了简化Henry函数的求解过程,Ohshima^[12]根据基本电动学公式及边界条件,采用试错法得到近似Henry函数的表达式

\begin{matrix} f (ka) = 1 + \frac{1}{2 [1 + δ / {(ka)]}^{3}} = 1 + \frac{1}{2 {1 + 2.5 / {ka [1 + 2 \exp {(- ka)]}}}^{3}} 。 (5) \end{matrix}

式中δ=b₁/[b₂+b₃exp(-ka)],三个参数b₁=2.5,b₂=1,b₃=2。通过比较Ohshima推导的近似Henry函数与Wiersema计算的精确Henry函数值发现,试错法对δ表达式形式的确定具有重要意义,但是三个参数的确定依然存在较大的主观性,导致当1<ka<100时,其相对误差最大为3%。在Ohshima推导的基础上,使用最小二乘曲线拟合算法^[13]对Wiersema计算的精确Henry函数值进行拟合,通过寻找数据的最佳匹配,确定δ表达式中三个参数的最优解分别为b₁=2.8,b₂=0.9,b₃=1,得到优化Henry函数表达式,Henry函数值更接近精确值。利用不同Henry函数表达式得到的曲线如图1所示。

\begin{matrix} f (ka) = 1 + \frac{1}{2 {1 + 2.8 / {ka [0.9 + \exp {(- ka)]}}}^{3}} 。 (6) \end{matrix}

图 1. 不同Henry函数得到的曲线

Fig. 1. Curves obtained by different Henry functions

下载图片查看所有图片

由图1可以看出,当ka<1或ka>20时,本文优化Henry函数与Henry推导出的分段函数基本重合;在1≤ka≤20范围内,本文优化Henry函数与Wiersema得到的精确Henry函数值基本重合,故得到的优化Henry函数表达式可以适用于所有的ka取值。不同Henry函数的误差对比如表1所示。

表 1. 不同Henry函数的误差对比

Table 1. Comparison of the errors of different Henry functions

ka	Wiersema	Ohshima		Optimization
ka	f(ka)	f(ka)	Error /%	f(ka)	Error /%
0.01	1.000	1.000	0	1.000	0
0.1	1.000	1.001	0.1	1.000	0
0.2	1.000	1.003	0.3	1.001	0.1
0.5	1.000	1.014	1.4	1.005	0.5
1	1.009	1.034	2.5	1.015	0.6
2	1.040	1.064	2.3	1.038	0.2
5	1.134	1.150	1.4	1.118	1.4
10	1.220	1.256	3.0	1.222	0.2
20	1.325	1.351	2.0	1.324	0.08
50	1.418	1.432	1.0	1.417	0.07
100	1.450	1.464	1.0	1.456	0.5
200	1.470	1.482	0.8	1.477	0.5
500	1.490	1.493	0.2	1.491	0.07
1000	1.500	1.496	0.3	1.495	0.3

查看所有表

由表1可以看出,当ka≪1时,Henry函数值可以近似取值为1;当ka>1000时,Henry函数值可近似取值为1.5。优化Henry函数比Ohshima推导的近似Henry函数精确度高,相对偏差小于1.5%,因此,在颗粒电泳迁移率相同的情况下,依据优化Henry函数计算的颗粒Zeta电位更接近真实值。

3 参数ka的确定

依据优化Henry函数计算f(ka)的值,就必须先确定ka的值。假设颗粒为刚性球体带电颗粒,其半径a可由动态光散射法测量得到,双电层厚度k^-¹可表示为^[14]

\begin{matrix} k^{- 1} = {(\frac{ε_{0} ε_{r} k_{B} T}{\overset{N}{\sum_{i = 1}} z_{i}^{2} e^{2} n_{i}^{\infty}})}^{\frac{1}{2}}, (7) \end{matrix}

式中 $\begin{matrix} n_{i}^{\infty} \end{matrix}$ 为溶液浓度,z_i为离子化合价。如果胶体中只含有一种电解质,双电层厚度可简化为

\begin{matrix} k^{- 1} = {(\frac{ε_{0} ε_{r} k_{B} T}{2000 e^{2} I \cdot N_{A}})}^{\frac{1}{2}}, (8) \end{matrix}

式中N_A表示阿伏伽德罗常数,I表示离子强度。因此,双电层厚度与离子强度有关,离子强度越大,双电层厚度越小;反之,双电层厚度越大。离子强度为

\begin{matrix} I = \frac{1}{2} \sum n_{i} z_{i}^{2}, (9) \end{matrix}

式中n_i为离子浓度,z_i为离子化合价。表2给出了电解质溶液浓度为c时,不同电解质类型的离子强度表达式。

表 2. 不同电解质类型的离子强度表达式

Table 2. Expressions of ionic strength for different types of electrolyte

Type of electrolyte	Ionic strength
1∶1	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (c×1²+c×1²)=c
1∶2 or 2∶1	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (2×c×1²+c×2²)=3c
2∶2	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (c×2²+c×2²)=4c
1∶3 or 3∶1	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (3×c×1²+c×3²)=6c
3∶3	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (c×3²+c×3²)=9c
2∶3 or 3∶2	I= $\begin{matrix} \frac{1}{2} \end{matrix}$ (3×c×2²+2×c×3²)=15c

查看所有表

由于带电颗粒不溶解于电解质溶液,故计算离子强度时的离子不包括带电颗粒本身。表3所示为25 ℃下,不同浓度、不同类型电解质对应的双电层厚度^[15]。

表 3. 不同浓度、不同类型电解质对应的双电层厚度

Table 3. Double layer thickness of different concentrations and different types of electrolyte

Type of electrolyte	Double layer thickness /nm
Type of electrolyte	10^-7 mol·L^-1	10^-6 mol·L^-1	10^-5 mol·L^-1	10^-4 mol·L^-1	10^-3 mol·L^-1	10^-2 mol·L^-1	10^-1 mol·L^-1
1∶1	962	304	96.2	30.4	9.62	3.04	0.962
1∶2 or 2∶1	555	176	55.5	17.6	5.55	1.76	0.555
2∶2	481	152	48.1	15.2	4.81	1.52	0.481
1∶3 or 3∶1	393	124	39.3	12.4	3.93	1.24	0.393
3∶3	321	101	32.1	10.1	3.21	1.01	0.321
2∶3 or 3∶2	248	78.5	24.8	7.85	2.48	0.785	0.248

查看所有表

由表3可以看出,当pH=7时,在超纯水中,只存在H⁺和OH^-离子,离子浓度为10^-7 mol·L^-1,双电层厚度为962 nm。当加入浓度为10^-3 mol·L^-1的KCl溶液时,双电层厚度减小为9.62 nm。若颗粒粒径为203 nm,由(8)式得到不同浓度、不同类型电解质下的ka曲线,如图2所示。

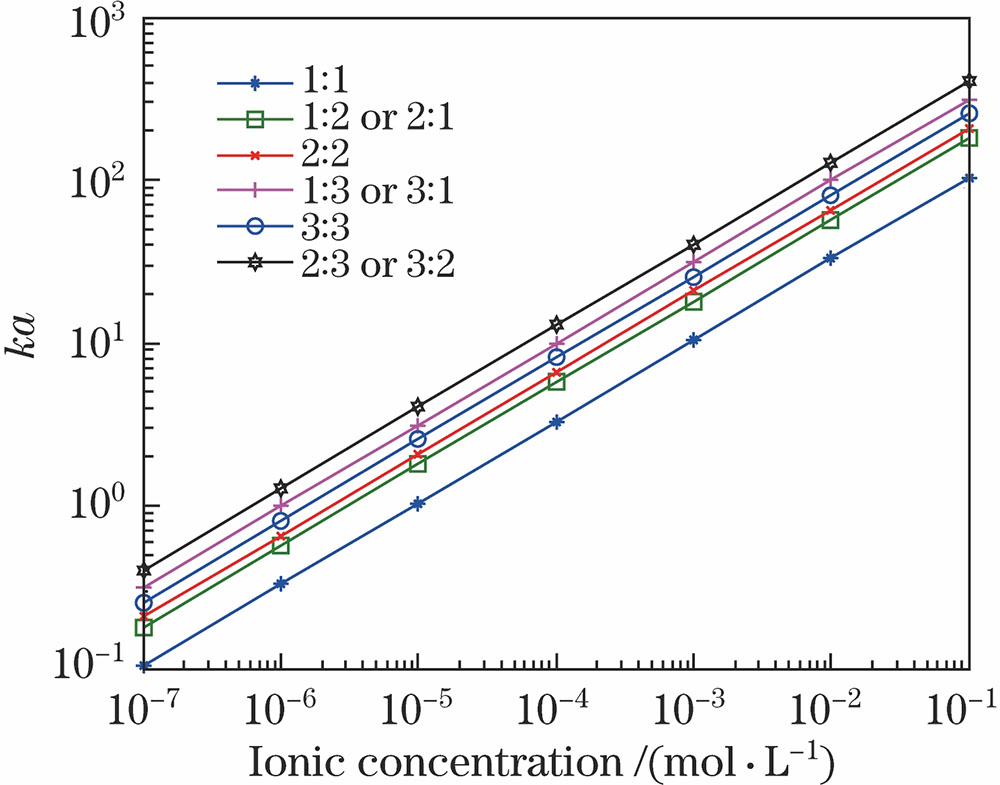
图 2. 不同浓度、不同电解质类型下的球形颗粒对应的ka曲线

Fig. 2. ka curves for spherical particles of different concentrations and different types of electrolyte

下载图片查看所有图片

由图2可以看出,相同类型的电解质,其ka值随电解质溶液浓度的升高而增大;相同浓度的溶液,电解质类型不同,其ka值也不相同。因此,电解质溶液浓度和电解质类型对ka值都有影响。图2可为所配制被测样品的ka值提供参考。

4 实验与数据分析

4.1 待测样品的制备

将质量为745,74.5,7.45 mg的KCl溶解后分别转移到100 mL容量瓶中,再分别加入0.02 mL质量分数为10%的聚苯乙烯乳胶球标准颗粒(5020A,Duke,美国)后加水定容,配置聚苯乙烯乳胶球体积质量为0.02 mg·mL^-1,KCl电解质浓度分别为10^-1,10^-2,10^-3 mol·L^-1的样品,编号分别为1、2、3。再配置一个体积为100 mL、分散在超纯水中、体积质量为0.02 mg·mL^-1的聚苯乙烯乳胶球样品,编号为4。配制样品时必须用超纯水,避免溶液中出现Ca²⁺、Ba²⁺等杂质而影响双电层的厚度。

4.2 Henry函数的计算

依据表1离子强度的计算式,编号为1、2、3的电解质溶液中含有K⁺、Cl^-离子的强度分别为

\begin{matrix} \{\begin{matrix} I_{1} = \frac{1}{2} (c \times 1^{2} + c \times 1^{2}) = \frac{1}{2} (0.1 \times 1^{2} + 0.1 \times 1^{2}) = 10^{- 1} mol \cdot L^{- 1} \\ I_{2} = \frac{1}{2} (c \times 1^{2} + c \times 1^{2}) = \frac{1}{2} (0.01 \times 1^{2} + 0.01 \times 1^{2}) = 10^{- 2} mol \cdot L^{- 1} \\ I_{3} = \frac{1}{2} (c \times 1^{2} + c \times 1^{2}) = \frac{1}{2} (0.001 \times 1^{2} + 0.001 \times 1^{2}) = 10^{- 3} mol \cdot L^{- 1} \end{matrix}, (10) \end{matrix}

因此,编号为1、2、3的样品中带电颗粒的双电层厚度分别为0.962,3.04,9.62 nm,编号为4的样品中带电颗粒的双电层厚度为962 nm。

以1号样品为例,温度为25 ℃时,测得水的黏度为0.8937×10^-3 Pa·s,KCl溶液的黏度为0.8854×10^-3 Pa·s,相对介电常数为78.5,真空中介电常数为8.854×10^-12 F·m^-1,玻尔兹曼常数为1.38×10^-23,样品中离子强度为I₁=10^-1 mol·L^-1,颗粒的电泳迁移率为5.590×10^-8 m²·(s·V)^-1,由(8)式求得双电层厚度为

\begin{matrix} k^{- 1} = {(\frac{ε_{r} ε_{0} k_{B} T}{2000 e^{2} I \cdot N_{A}})}^{\frac{1}{2}} = {[\frac{78.5 \times 8.854 \times 10^{- 12} \times 1.38 \times 10^{- 23} \times 298.13}{2000 \times (1.6022 \times 10^{- 19})^{2} \times 10^{- 1} \times 6.022 \times 10^{23}}]}^{\frac{1}{2}} \approx 0.962 nm 。 (11) \end{matrix}

使用纳米粒度仪测得5020A聚苯乙烯颗粒的粒径为203 nm,则颗粒半径与双电层厚度之比为ka=a/k^-1=101.5/0.962=105.51。

利用三次样条曲线插值算法,对Wiersema提供的Henry函数值进行插值,当ka=105.51时,得到精确Henry函数值为f(ka)₀=1.4528。根据(5)式求得近似Henry函数值为

\begin{matrix} f {(ka)}_{1} = 1 + \frac{1}{2 {1 + 2.5 / {ka [1 + 2 \exp {(- ka)]}}}^{3}} = 1 + \frac{1}{2 {\{1 + \frac{2.5}{105.51 \times [1 + 2 \exp (- 105.51)]}\}}^{3}} = 1.4661, (12) \end{matrix}

根据(6)式求得优化Henry函数值为

\begin{matrix} f {(ka)}_{2} = 1 + \frac{1}{2 {1 + 2.8 / {ka [0.9 + \exp {(- ka)]}}}^{3}} = 1 + \frac{1}{2 {\{1 + \frac{2.8}{105.51 \times [0.9 + \exp (- 105.51)]}\}}^{3}} = 1.4583, (13) \end{matrix}

依据上述方法,得到所有样品的不同Henry函数值,如表4所示。

表 4. 待测样品的Henry函数值

Table 4. Henry function for the samples to be measured

Parameter	Sample 1	Sample 2	Sample 3	Sample 4
a /nm	101.5	101.5	101.5	101.5
1/k /nm	0.962	3.04	9.62	962
ka	105.51	33.388	10.551	0.1055
f(ka)₀	1.4528	1.3961	1.2267	1.0000
f(ka)₁	1.4661	1.4026	1.2642	1.0006
f(ka)₂	1.4583	1.3827	1.2303	1.0001

查看所有表

4.3 Zeta电位的测量

利用图3所示的电泳光散射装置,测量带电颗粒在电场中的电泳迁移率,测量原理可参考文献[ 16]。

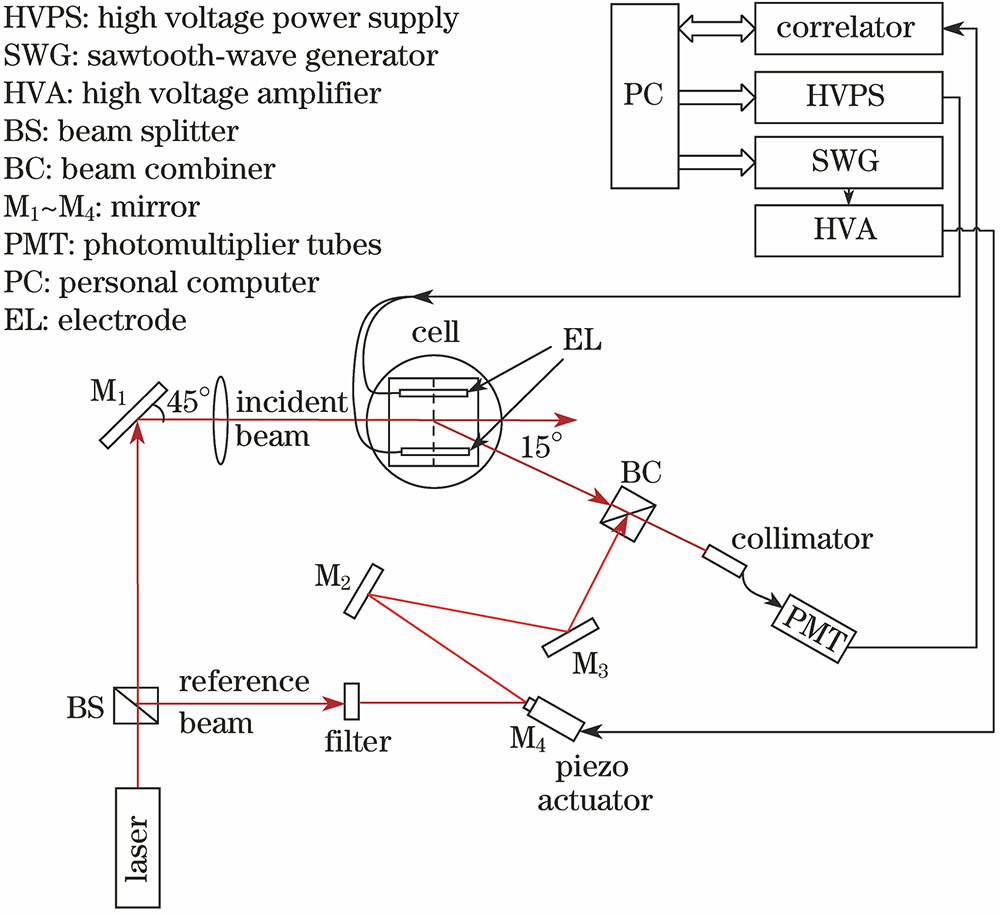
图 3. 电泳光散射法测量装置结构图

Fig. 3. Schematic of the electrophoretic light scattering experiment setup

下载图片查看所有图片

以1号样品为例,f(ka)的不同取值见表4,当颗粒电泳迁移率μ为-2.992×10^-8 m²·(s·V)^-1时,依据精确Henry函数值f(ka)₀=1.4528,根据(1)式求得颗粒Zeta电位ζ₀为

\begin{matrix} ζ_{0} = \frac{3 ημ}{2 ε_{r} ε_{0}} \frac{1}{f (ka)} = \frac{3 \times 0.885 \times 10^{- 3} \times (- 2.992 \times 10^{- 8})}{2 \times 78.5 \times 8.854 \times 10^{- 12}} \times \frac{1}{1.4528} \times 10^{3} \approx - 39.4 mV 。 (14) \end{matrix}

依据Ohshima推导的近似Henry函数值f(ka)₁=1.4661求得颗粒Zeta电位ζ₁=-39.0 mV,依据优化Henry函数值f(ka)₂=1.4583求得颗粒Zeta电位ζ₂为-39.2 mV,对4种样品分别进行了6次实验,实验结果如表5所示。

表 5. 采用不同Henry函数时颗粒Zeta电位值的比较

Table 5. Comparison of Zeta potentials calculated by different Henry functions

No.	Sample 1				Sample 2				Sample 3				Sample 4
No.	μ	ζ₀	ζ₁	ζ₂	μ	ζ₀	ζ₁	ζ₂	μ	ζ₀	ζ₁	ζ₂	μ	ζ₀	ζ₁	ζ₂
1	-2.992	-39.4	-39.0	-39.2	-4.284	-58.8	-58.3	-59.2	-5.590	-87.3	-84.5	-86.8	-3.316	-64.1	-63.7	-64.1
2	-3.085	-40.6	-40.2	-40.4	-4.165	-57.1	-56.7	-57.5	-5.533	-86.4	-83.6	-85.9	-3.345	-64.7	-64.3	-64.6
3	-2.895	-38.2	-37.7	-37.9	-4.140	-56.8	-56.4	-57.2	-5.567	-86.9	-84.1	-86.4	-3.368	-65.1	-64.7	-65.1
4	-2.930	-38.6	-38.2	-38.4	-4.222	-58.0	-57.5	-58.3	-5.392	-84.2	-81.5	-83.7	-3.409	-65.9	-65.5	-65.9
5	-3.063	-40.4	-39.9	-40.1	-4.133	-56.7	-56.3	-57.1	-5.388	-84.1	-81.4	-83.6	-3.399	-65.7	-65.3	-65.7
6	-2.984	-39.3	-38.9	-39.1	-4.312	-59.1	-58.7	-59.6	-5.546	-86.6	-83.8	-86.1	-3.434	-66.4	-66.0	-66.3
Average	-2.992	-39.4	-39.0	-39.2	-4.209	-57.8	-57.3	-58.2	-5.503	-85.9	-83.2	-85.4	-3.379	-65.3	-64.9	-65.3
Relative error /%	-	-	1.0	0.5	-	-	0.9	0.7	-	-	3.1	0.6	-	-	0.5	0
Repeatability /%	-	-	2.5	2.4	-	-	1.8	1.8	-	-	1.6	1.6	-	-	1.3	1.3

查看所有表

由实验结果可以看出,随着电解质溶液浓度的升高,其颗粒电泳迁移率和Zeta电位逐渐减小。通过优化Henry函数计算得到的颗粒Zeta电位值,与Ohshima推导的近似Henry函数计算的颗粒Zeta电位值相比,相对误差由大于3.0%减小到小于1.0%,计算结果更加精确。

5 结论

为提高Henry函数的精度,利用最小二乘算法在0.01<ka<10000范围内拟合Wiersema计算的精确Henry函数值,获得了优化的Henry函数表达式。实验结果表明,与Ohshima推导的近似Henry函数相比,优化后的Henry函数可以有效提高Zeta电位的计算精度,计算结果的相对误差小于1.0%。如果被测颗粒分散在超纯水或有机分散剂中,此时ka≪1,Henry函数值可近似为1.0;如果被测颗粒粒径远远大于200 nm,且电解质溶液浓度大于10^-2 mol·L^-1,此时ka>1000,Henry函数值可近似为1.5。

参考文献

[1] Paz-Garcia J M, Johannesson B, Ottosen L M, et al. . Modeling of electric double-layers including chemical reaction effects[J]. Electrochimica Acta, 2014, 150: 263-268.

Paz-Garcia J M, Johannesson B, Ottosen L M, et al. . Modeling of electric double-layers including chemical reaction effects[J]. Electrochimica Acta, 2014, 150: 263-268.

[2] Thomas J C, Hanton K L, Crosby B J. Measurement of the field dependent electrophoretic mobility of surface modified silica/AOT suspensions[J]. Langmuir, 2008, 24(19): 10698-10701.

Thomas J C, Hanton K L, Crosby B J. Measurement of the field dependent electrophoretic mobility of surface modified silica/AOT suspensions[J]. Langmuir, 2008, 24(19): 10698-10701.

[3] GreatzL. Handbuch der elektrizitat und des magnetismus[M]. Leipzig:1921.

GreatzL. Handbuch der elektrizitat und des magnetismus[M]. Leipzig:1921.

[4] Huckel E. Die kataphorese der kugel[J]. Physik Z, 1924, 25: 204-210.

Huckel E. Die kataphorese der kugel[J]. Physik Z, 1924, 25: 204-210.

[5] Henry DC. The cataphoresis of suspended particles. Part Ⅰ. The equation of cataphoresis[C]. Proceedings of the Royal Society of London, A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1931, 133( 821): 106- 129.

Henry DC. The cataphoresis of suspended particles. Part Ⅰ. The equation of cataphoresis[C]. Proceedings of the Royal Society of London, A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1931, 133( 821): 106- 129.

[6] Overbeek J T G. Quantitative interpretation of the electrophoretic velocity of colloids[J]. Advances in Colloid Science, 1950, 3: 797-823.

Overbeek J T G. Quantitative interpretation of the electrophoretic velocity of colloids[J]. Advances in Colloid Science, 1950, 3: 797-823.

[7] Wiersema P H, Loeb A L. Overbeek J T G. Calculation of the electrophoretic mobility of a spherical colloid particle[J]. Journal of Colloid and Interface Science, 1966, 22(1): 78-99.

Wiersema P H, Loeb A L. Overbeek J T G. Calculation of the electrophoretic mobility of a spherical colloid particle[J]. Journal of Colloid and Interface Science, 1966, 22(1): 78-99.

[8] O'Brien R W. White L. Electrophoretic mobility of a spherical colloidal particle[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1978, 74(1): 1607-1626.

O'Brien R W. White L. Electrophoretic mobility of a spherical colloidal particle[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1978, 74(1): 1607-1626.

[9] Ohshima H, Healy T W, White L. Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1983, 79(11): 1613-1628.

Ohshima H, Healy T W, White L. Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions[J]. Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics, 1983, 79(11): 1613-1628.

[10] Henderson D, Blum L. The Gouy-Chapman theory as a special case of the hypernetted chain approximation[J]. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 1978, 93(2): 151-154.

Henderson D, Blum L. The Gouy-Chapman theory as a special case of the hypernetted chain approximation[J]. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, 1978, 93(2): 151-154.

[11] Miller JF. The determination of very small electrophoretic mobilities of dispersions in non-polar media using phase analysis light scattering[D]. Bristol: University of Bristol, 1990.

Miller JF. The determination of very small electrophoretic mobilities of dispersions in non-polar media using phase analysis light scattering[D]. Bristol: University of Bristol, 1990.

[12] Ohshima H. A simple expression for Henry's function for the retardation effect in electrophoresis of spherical colloidal particles[J]. Journal of Colloid and Interface Science, 1994, 168(1): 269-271.

Ohshima H. A simple expression for Henry's function for the retardation effect in electrophoresis of spherical colloidal particles[J]. Journal of Colloid and Interface Science, 1994, 168(1): 269-271.

[13] Coleman T F, Li Y Y. An interior trust region approach for nonlinear minimization subject to bounds[J]. SIAM Journal on Optimization, 1994, 6(2): 418-445.

Coleman T F, Li Y Y. An interior trust region approach for nonlinear minimization subject to bounds[J]. SIAM Journal on Optimization, 1994, 6(2): 418-445.

[14] Hunter RJ. Zeta potential in colloid science: principles and applications[M]. London: Academic Press, 2013.

Hunter RJ. Zeta potential in colloid science: principles and applications[M]. London: Academic Press, 2013.

[15] 刘伟, 张珊珊, John C. Thomas, 等. 基于频谱细化算法的电泳光散射Zeta电位测量方法[J]. 光学学报, 2017, 37(2): 0229001.

刘伟, 张珊珊, John C. Thomas, 等. 基于频谱细化算法的电泳光散射Zeta电位测量方法[J]. 光学学报, 2017, 37(2): 0229001.

Liu Wei, Zhang Shanshan, John C. Thomas, et al. Zeta potential measurement method of electrophoretic light scattering based on Chirp Z-transform[J]. Acta Optica Sinica, 2017, 37(2): 0229001.

秦福元, 刘伟, 王文静, JohnC.Thomas, 王雅静, 申晋. Zeta电位计算过程中Henry函数的优化表达式[J]. 光学学报, 2017, 37(10): 1029003. Fuyuan Qin, Wei Liu, Wenjing Wang, C. Thomas John, Yajing Wang, Jin Shen. An Optimal Expression for Henry Function for the Calculation of Zeta Potential[J]. Acta Optica Sinica, 2017, 37(10): 1029003.

Zeta电位计算过程中Henry函数的优化表达式下载： 837次

1 引言

2 Henry函数的优化近似表达式

图 1. 不同Henry函数得到的曲线

Fig. 1. Curves obtained by different Henry functions

表 1. 不同Henry函数的误差对比

Table 1. Comparison of the errors of different Henry functions

3 参数ka的确定

表 2. 不同电解质类型的离子强度表达式

Table 2. Expressions of ionic strength for different types of electrolyte

表 3. 不同浓度、不同类型电解质对应的双电层厚度

Table 3. Double layer thickness of different concentrations and different types of electrolyte

图 2. 不同浓度、不同电解质类型下的球形颗粒对应的ka曲线

Fig. 2. ka curves for spherical particles of different concentrations and different types of electrolyte

4 实验与数据分析

4.1 待测样品的制备

4.2 Henry函数的计算

表 4. 待测样品的Henry函数值

Table 4. Henry function for the samples to be measured

4.3 Zeta电位的测量

图 3. 电泳光散射法测量装置结构图

Fig. 3. Schematic of the electrophoretic light scattering experiment setup

表 5. 采用不同Henry函数时颗粒Zeta电位值的比较

Table 5. Comparison of Zeta potentials calculated by different Henry functions

5 结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

Zeta电位计算过程中Henry函数的优化表达式 下载： 837次

1 引言

2 Henry函数的优化近似表达式

图 1. 不同Henry函数得到的曲线

Fig. 1. Curves obtained by different Henry functions

表 1. 不同Henry函数的误差对比

Table 1. Comparison of the errors of different Henry functions

3 参数ka的确定

表 2. 不同电解质类型的离子强度表达式

Table 2. Expressions of ionic strength for different types of electrolyte

表 3. 不同浓度、不同类型电解质对应的双电层厚度

Table 3. Double layer thickness of different concentrations and different types of electrolyte

图 2. 不同浓度、不同电解质类型下的球形颗粒对应的ka曲线

Fig. 2. ka curves for spherical particles of different concentrations and different types of electrolyte

4 实验与数据分析

4.1 待测样品的制备

4.2 Henry函数的计算

表 4. 待测样品的Henry函数值

Table 4. Henry function for the samples to be measured

4.3 Zeta电位的测量

图 3. 电泳光散射法测量装置结构图

Fig. 3. Schematic of the electrophoretic light scattering experiment setup

表 5. 采用不同Henry函数时颗粒Zeta电位值的比较

Table 5. Comparison of Zeta potentials calculated by different Henry functions

5 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

Zeta电位计算过程中Henry函数的优化表达式下载： 837次