1. INTRODUCTION

Phase imaging focuses on obtaining spatial phase distribution of objects in specific application scenarios, for instance, cell microscopic imaging in biomedicine and wavefront aberration detection in atmospheric optics. Particularly, for objects that are transparent or have uniform amplitude transmittance, reconstructing the wavefront can visualize the spatial distribution of effective information such as thickness and refractive index. However, since the available light sensors can only record the intensity of the signal, the ingenious phase recording method and phase retrieval process from the intensity measurement are necessary. The most typical method of recording and restoring phase information is known as digital holography (DH) [1] or digital holographic microscopy (DHM) [24" target="_self" style="display: inline;">–4], which is based on interferometry. DH makes full use of photoelectric imaging techniques and computer techniques, and it has steadily developed and gradually matured in the fields of medical diagnosis [5], dynamic three-dimensional display [6], information encryption [7], and so on. Nevertheless, most of the basic interferometric systems for holographic recording require the introduction of an additional reference arm; otherwise, the reconstruction is disturbed by twin images, and thus the optical configuration is difficult to simplify and lacks flexibility. In contrast, there are several reference-free conventional phase imaging methods, such as the transport of intensity equation (TIE)- [810" target="_self" style="display: inline;">–10], coherent diffraction imaging (CDI)- [11,12], and compressive sensing (CS)-based methods [1315" target="_self" style="display: inline;">–15]. Among them, TIE is simple in calculation due to its analytical solution, but it requires multiple intensity measurements and usually has the problem of being sensitive to the map boundaries [16]. CDI- and CS-based methods primarily implement phase estimation with the so-called phase retrieval algorithm or sparsity-based optimization algorithm. The phase retrieval iterative algorithms widely used in optical imaging are known as the Gerchberg–Saxton algorithm (GSA) [17] and its improved algorithms [18,19]. For starting an iterative process, the intensity of the multiplane defocused images or a single diffraction intensity distribution with known a priori of the sample should be taken [1921" target="_self" style="display: inline;">–21]. Despite this, the conventional iterative approaches require tedious system alignment or suffer from the inherent iteration stagnation problems. The cumbersome configuration procedures and low computational efficiency therefore lead to defects in terms of the real-time performance and the stability of these imaging systems.

Deep learning, a rapidly developing artificial intelligence technology, has shown great potential for application in various imaging techniques, ranging from image-based wavefront sensing [22–25" target="_self" style="display: inline;">–25], holographic image reconstruction [26–29" target="_self" style="display: inline;">–29], coherent diffraction imaging [30,31], to inversion of multiple scattering [32–35" target="_self" style="display: inline;">–35]. Compared with most conventional methods, artificial neural networks provide a more efficient end-to-end solution to the inverse problem in optical imaging. For example, the convolutional neural network (CNN) can autonomously and effectively eliminate the twin-image and spatial artefacts of digital holography [26] or directly reconstruct phase targets from diffraction images [30]. According to the powerful self-organizing ability and adaptive characteristics of deep neural networks (DNNs), it is also used to solve the problem of phase retrieval or object detection in optical scattering [32–36" target="_self" style="display: inline;">–36]. DNN is proved to be able to learn the nonlinear relationship between the output speckle intensity pattern of the scattering medium and the input object [3436" target="_self" style="display: inline;">–36]. However, in these cases, scattering is generally considered to scramble and hinder the propagation of light, and reconstruction is only applicable to objects with simple structures (e.g., a single digit or letter, etc.). In the recent research on computational imaging methods, we have seen that scattering media have excellent natural properties that can be used for optical signal preprocessing such as analog compressive sensing [37]. References [38,39] demonstrate the harmonious combination of this preconditioner and deep learning, i.e., compressive sampling with thick scattering media and imaging with low-bit-depth or undersampled measurements. It is a good revelation about the dimensionality reduction of data through physical processes and subsequent efficient reconstruction using the network. Since the bandwidth required for image data transmission depends on the image resolution and its bit depth, collecting and processing low-dimensional data could reduce the cost of hardware devices and improve transmission efficiency, which is especially significant for large-scale data.

In this paper, with the support of deep learning, we propose a method for phase imaging via weak scattering, which enables the reconstruction of the complicated object using only a single low-bit or binary pattern. By simply placing a random phase mask/plate in front of the image sensor to preprocess the wavefront, a series of diffraction intensity images produced by different incoming wavefronts are converted into highly consistent speckle patterns. The speckle patterns are essentially composed of many speckle grains and thus contain abundant recognizable features. Due to spatial shift invariance, the slight spatial geometric distortion of these features can be implicitly related to the wavefront phase. Our model shows that the sparse binary pattern can preserve the distortion of the speckle field through partial features. After being learned by DNN, these low-bit patterns containing less content could be used to almost recover actual phase objects. Our method is totally reference free and circumvents the twin-image problem in digital holographic reconstruction [26] or the establishment of multiplane constraints as required by other conventional phase imaging methods [8–12" target="_self" style="display: inline;">–12]. More importantly, the data compressibility in our method is verified. Unlike the performance of analog optical compressive sensing methods that depend on the sparsity of the object [37,38], we experimentally demonstrated the faithful reconstruction utilizing low-bit patterns, even for phase objects with complex structures.

2. METHOD

2.1 A. Physical Model

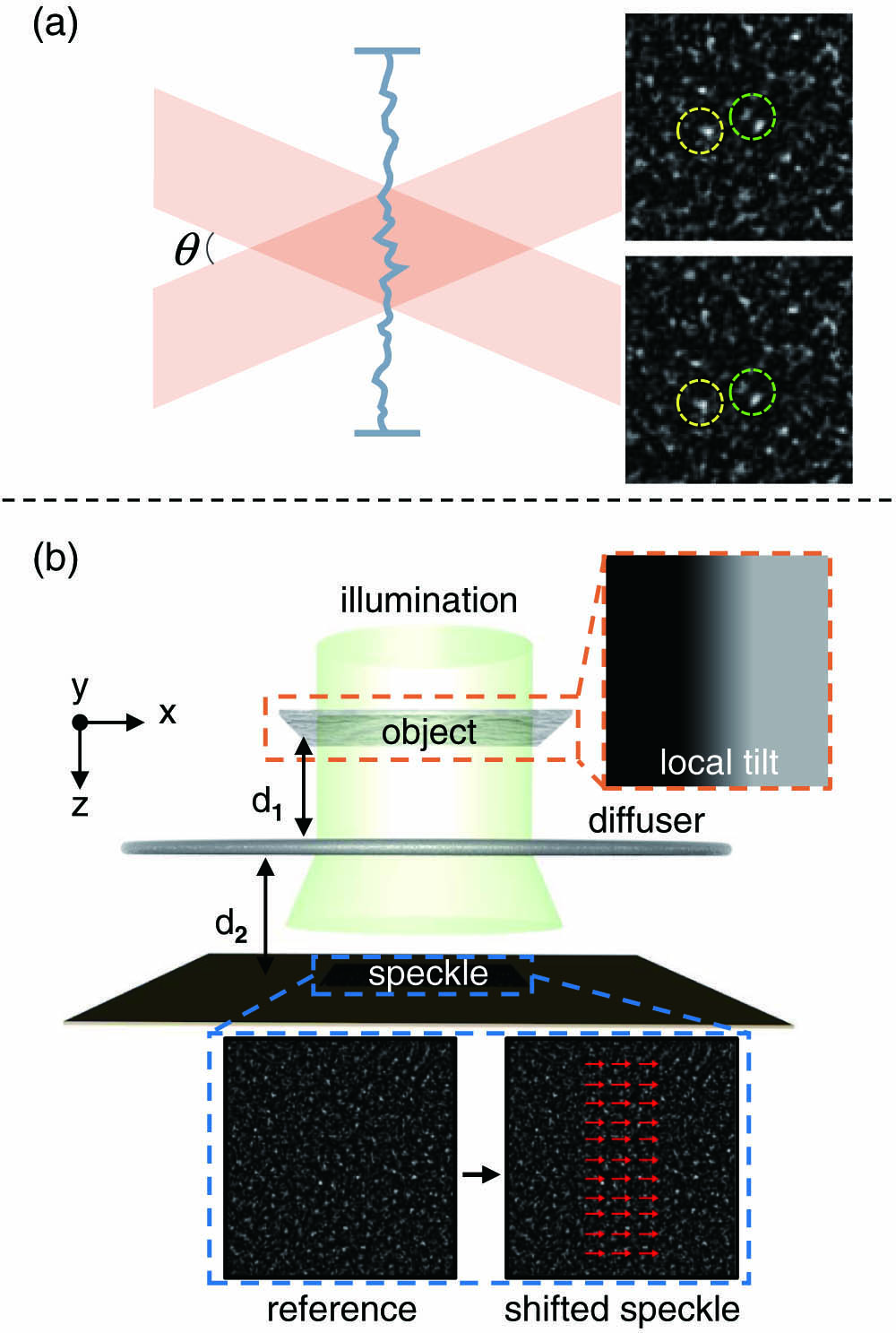
Generally, shift invariance means that for a system, the only change in its response signal is the same temporal or spatial shift that occurs in the input signal. An optical system with an aperture is a typical spatial shift-invariant system. In the case of paraxial approximation, slight adjustment of the incident angle of the object light will produce a similar pattern in the image space but only introduce a displacement related to the incident angle. For a lens imaging system, shift invariance under paraxial conditions can be expressed as and where L{·} is the point spread function (PSF), and f and g denote the input and response of the system, namely, the object field and the image field. If the pattern represented by g(x,y), on the right side of Eq. (1), carries certain features, then g(x−α,y−β) also completely retains these features. The only difference between the two patterns recorded by the sensor is the lateral displacement caused by α and β. Further, the same phenomenon will also occur when the lens is replaced with another phase mask, e.g., a random phase mask [40]. As shown in Fig. 1(a), for plane wave incidence without carrying any information, we will eventually observe a random speckle pattern in the image plane when light passes through a phase mask with a Gaussian distribution. Like the convergence of a convex lens on a plane wavefront, the phase profile of the mask can be regarded as an inherent distortion applied to the wavefront. Here, Eqs. (1) and (2) can also be used to describe the shift invariance of this system.

Fig. 1. (a) Beam passes through an ideal random phase mask with negligible thickness and speckles generated by two light beams with different incident angles. The two speckle patterns show high similarity, and the speckle grains in the circles indicate the same local features. (b) Conceptual demonstration of the optical memory effect. Placing a phase object causes a local tilt of the incident light wavefront, which results in a partial translation of the speckle.

下载图片 查看所有图片

Now, consider a nonuniform wavefront, that is, a light field containing object information. Figure 1(b) shows the recording of the speckle pattern generated by an object with only a local tilt phase, where the coherent beam propagating along the z axis passes through the phase object and illuminates the diffuser. The speckle pattern T(x,y) generated by the transmitted light field in the detection plane is viewed as the measurement of the encoded object light information. By taking away the object, a reference speckle pattern R(x,y) can be obtained, whose intensity distribution comes entirely from the diffuser without impact from the geometric deformation of the wavefront caused by the object. The reference pattern and the shifted pattern, formed within the shift-invariant range, allow us to visually observe the local slight shift of speckles introduced by the object wavefront. For a local tilt phase with angle θ, as long as θ is within the shift-invariant range, the local intensity distribution in T(x,y) shifted by Δs=(α,β) compared to R(x,y) will retain the pattern feature almost identical to those in R(x,y), that is, T(x−α,y−β)=R(x,y). Here, for a small θ, we get Δs=θ·d2, where d2 refers to the distance from the mask to the sensor.

Distinct from the diffraction pattern generated by the phase object at a given distance, the speckles formed from a random mask can be accompanied by fixed recognizable features such as the distribution of speckles and the shape of speckle grains [see Fig. 1(a)]. Within the shift-invariant range, arbitrary input wavefronts will cause distortion of the speckle field but will not destroy the local similarity of these features of the speckles before and after the distortion. According to the discussion above, this phenomenon could establish an implicit relationship between the spatial variation of local features in the pattern and the phase distribution of the corresponding wavefront. However, if the consideration is to extract the wavefront phase from the distortion of the acquired pattern, the full intensity measurement of the speckle field may not be necessary in the presence of recognizable features.

Binarization can reduce the data size of the image while highlighting the outline of the content in the image. For the speckle pattern in our model, the speckle features associated with geometric distortion and local variations in the raw measurement can be partially preserved after binarization. From the perspective of the ability of neural networks to extract features and fit complex functions, the designed samples can be used to train the network to learn the desired inference but avoid establishing a specific functional relation or mathematical operation. Our DNN is trained to directly decode the phase from the aforementioned binary or low-bit-depth pattern containing a small amount of content.

Additionally, as illustrated in Fig. 1(b), a commercial thin diffuser is used in the experiment to replace the ideal phase mask mentioned in the above physical model. This diffuser can be thought of as a single-sided rough thin scatterer with weak scattering events, whose shift invariance is only valid in a limited angular range, called the “optical memory effect range” [40–44" target="_self" style="display: inline;">–44]. For a common scattering medium, the memory effect range is usually related to its thickness and the sizes of the medium grains [40]. This range of the diffuser we use will be mentioned later in the experimental setup; it is wide enough for our imaging task.

2.2 B. Experimental Setup

The optical experimental setup for data acquisition and imaging is illustrated in Fig. 2(a). The pure phase object is loaded onto the phase-only spatial light modulator (SLM, Holoeye PLUTO-2, 1920×1080, pixel pitch 8.0 μm) after being calibrated by the SLM response curve, first coherently illuminated by a collimated beam from a laser source (LR−GSP−520/1∼40mW, 520 nm). Then the modulated incident light is reflected by the SLM and reaches the front surface of the diffuser [Edmund Optics, holographic, diffusing angle (FWHM)=1°±1°, 0.78 mm] with a free-space propagation distance of d1=10mm. The camera sensor (Thorlabs, DCC1545M, 1280×1024, pixel size 5.2 μm, ADC resolution 10 bit) is finally placed at a short distance of d2 (5–60 mm) from the rear surface of the diffuser to capture the intensity of the transmitted light. Note that because of the difference in pixel size between the SLM and the camera sensor, the spatial ratio of the object plane and the imaging plane needs to be matched, and thus we place a 4−f (f1=300mm, f2=250mm) system between the SLM and the camera and crop only the square area of 398×398 pixels of the SLM and 512×512 pixels of the camera sensor for experimentation [see Fig. 2(a)].

Fig. 2. Experimental setup for speckle pattern acquisition. Phase objects are loaded by the spatial light modulator. The thin diffuser is placed at the back focal plane of the 4−f system. (a) Designated speckle acquisition window (white dotted line box). (b) Autocorrelation of speckle patterns at different diffraction distances d2 and the correlation width is ∼20μm. (c) Cross-correlation coefficients between speckle patterns corresponding to different incoming wavefronts at distances d2 varying from 5 to 80 mm. POL, linear polarizer; SLM, spatial light modulator; BS, beam splitter; CAM, camera.

下载图片 查看所有图片

Importantly, the holographic diffuser produces weak scattering events and holds a very large memory-effect range (almost 0.3 rad as characterized by Berto et al. [45]). The autocorrelation operation of the captured speckle intensity pattern is performed to obtain the size grains. Figure 2(b) shows the speckle correlation width of approximately 20 μm at different diffuser-to-camera distances, which is well resolved by the camera and convolution filters.

2.3 C. Architecture of the DNN

As a supervised learning model, the general architecture of the DNN is illustrated in Fig. 3. It has a typical U-net [46] architecture and consists of an encoder and a decoder. The compressed (low-bit) pattern or captured raw speckle pattern is first put into the network. After being convolved with a 3×3 filter, it is encoded by successively passing through five combinations of dense block and pooling layers and a separate dense block. The image size of the encoder output is reduced with a rate of 16 times laterally, but it carries a large number of deep features of the input image in the longitudinal direction. Next, the encoded feature map is magnified to the lateral size of the original input image by a decoder consisting of five dense blocks and upsampling convolutional layers. Since the symmetry of the model causes the degradation of features, in order to improve the characterization ability of the DNN and solve the problem of gradient disappearance, skip connections are used to enhance the transmission of features. The final estimate is then generated through a convolutional layer with a kernel size of 1×1, which contains one channel for outputting the phase map.

Fig. 3. Schematic diagram of the proposed method for phase imaging and the basic architecture of CNN. The input to the network is a single-shot low-bit pattern or raw intensity measurement.

下载图片 查看所有图片

In the process of training the neural network, we use mean squared error (MSE) and structural similarity index (SSIM) [47] as loss functions to evaluate the performance of DNN. The MSE and the SSIM are defined as and respectively. Here m represents the number of input samples in the MSE, that is, the number of elements contained in a batch; y^ is the output of the network, while y indicates the ground truth. For Eq. (4), ⟨·⟩ performs the operation of calculating the overall average, and the constants c1, c2, and c3 ensure the stability of the denominator. The SSIM is a combination of three indicators that imply luminance, contrast, and structure, which is ideal for evaluating image quality. The final expression of the loss function, combining the above two loss functions, is defined as where the coefficients α and β adjust the weights of the two functions and satisfy the condition of α+β=1. During the simulation and experiment, we found that higher reconstruction quality can be obtained by setting α to 0.85 and β to 0.15.

2.4 D. Network Training

For data acquisition, we use two different classes of phase objects, namely, random grayscale maps with smooth phase and images from the Faces-LFW [48] database with complex structure and large phase gradient. For the former, we generate the datasets by using a bilinear interpolation method to resize a low-resolution (5×5) random matrix to a large size (398×398) as the phase object loaded onto the SLM, and then we crop the corresponding area of the raw speckle pattern captured by the camera sensor [Fig. 2(a)]. Taking into account the diffraction and diffusing angles, the size of the cropped portion is 512×512 pixels, which is slightly larger than the actual size of the phase object on the SLM. After compressing the raw measurement into low-bit patterns with different degrees, there are finally 7000 different pairs of images: 5000 for training, 1000 for validation, and 1000 for testing. For the latter, we interpolate the human face image to 398×398 and perform the same input image data acquisition and processing, including 7000 training samples, 2000 validation samples, and 1000 testing samples. The entire training of the network is performed on two GPUs (NVIDIA GeForce GTX 1080Ti) using the Adam optimizer, and the learning rate with an initial value of 10−3 and halved every 10 epochs is set. It takes about 2 h and 3 h for two classes of samples over a total of 30 epochs.

3. RESULTS AND DISCUSSION

3.1 A. Imaging Using Raw Measurement

Without loss of generality, the built neural network is first trained for imaging with uncompressed measurements. Also based on the memory effect, a method of reconstructing the wavefront by calculating the speckle displacement vector field through the registration algorithm (called the “Demon Algorithm”) [45] is used as a comparison to glimpse the performance improvement of using DNN. The experimental reconstruction results of random phase and human face images with comparative experiments are shown in Fig. 4(a) and Fig. 4(b), respectively. We adopt SSIM to quantitatively analyze the reconstruction quality of objects. Different distances of d2 (set to 60, 30, 10, and 5 mm) between the diffuser and the sensor are set in the experiment. Table 1 summarizes the reconstruction quality of the phase object in the two methods, where SDVF represents the method based on the speckle displacement vector field, and mean value 1 and mean value 2 indicate the average values of SSIM of the phase predictions in Fig. 4(a) and Fig. 4(b), respectively.

Fig. 4. Experimental results of phase recovery on (a) random grayscale image datasets (i–iii) and (b) human face datasets (iv–vi) with different diffraction distances d2. The images in leftmost column of each graph block are the speckle patterns, and the phase maps in the blue and the orange solid line boxes are estimates implemented by SDVF and DNN, respectively.

下载图片 查看所有图片

For pure phase objects, the first thing worth noting is that DNN can implement accurate inversion of weak scattering with only intensity images, which could be contrasted with detecting amplitude objects against scattering events [32–35" target="_self" style="display: inline;">–35]. Second, the phenomenon we observed is that the distance between the detection plane and the diffuser will influence the image quality. Both methods could achieve the best results when d2 is the minimum we set, but they suffer from a reduction in reconstruction accuracy when distance is increased. However, as shown in Fig. 4, this performance degradation seems to be more significant in the algorithm based solely on speckle correlation than in DNN. Figure 2(c) plots the curves of the cross-correlation coefficients between the speckle patterns corresponding to various incoming wavefronts. The variation in the local speckle distribution becomes more sensitive to the wavefront phase gradient as the propagation distance of d2 increases, which could be attributed to the diffusion of light and the superposition of adjacent speckle areas formed by various angular spectrum components after being expanded. Observing the speckle patterns in Fig. 4, the intensity measurements formed by three different wavefronts show a high similarity in speckle distribution and grain features when d2=5mm, while this correlation of the measurements with larger distances, e.g., d2=30mm and 60 mm, is destroyed, and the overall speckle distributions corresponding to different wavefronts can be clearly distinguished. What can be seen in Fig. 4 is that this change in similarity of the raw speckle patterns does not seem to seriously affect the imaging quality of the network. Despite this, the high similarity of speckle patterns is beneficial for removing redundant information, which will be demonstrated experimentally in the next section.

3.2 B. Low-Bit Imaging

The essence of compression is to eliminate redundant parts of data to achieve optimization of data acquisition, processing, and storage. In our experiment, compressing the bit depth of the pattern means discarding most of the intensity information of the raw measurement. But indeed, in this way, we confirmed the redundancy of intensity information for phase imaging in the experiment. DNN can achieve the same inference as in Section 3.A using only partial features retained from the raw measurement. Specifically, we apply binarization and bit depth conversion to the acquired raw measurements according to the set intensity/grayscale thresholds. Taking into account the time-varying brightness of captured pattern result from the unstable power of the laser and ambient light, with the uniform illumination, the selection of the conversion threshold for each measurement is considered to be related to its average intensity for convenience. A 1 bit pattern is made by setting the pixel values of the raw measurement greater than the average intensity to 1 and the rest to 0. For the conversion of other bit depths, we use many-to-one mapping, that is, we multi-equalize the normalized intensity range and correspond to the low bit value. Figure 5(a) shows the raw measurement and its two processed low-bit patterns, which preserve the basic shapes and distribution of speckle grains.

Fig. 5. (a) Raw measurement and processed patterns with different bit depth; (b) SSIM of the reconstructions at each image bit depth.

下载图片 查看所有图片

After training with the processed datasets, the network shows satisfactory performance on reconstructing the object using only binary or low-bit patterns. As illustrated in Fig. 6, we list the imaging results of the phase objects with d2=5mm (the distance between the diffuser and the camera) and set the reconstruction results with d2=60mm as comparison. For all datasets, the improvement of bit depth on imaging quality is also tested. The bar graph for the average SSIM over testing samples with different processed bit depths is plotted in Fig. 5(b), where the average value is obtained from a total of 120 samples for each bit depth. The graph also compares the performance of the neural network for the imaging of the two types of samples. On the whole, higher reconstruction precision is achieved on objects with smooth phase distribution, and increasing the bit depth of the datasets can more effectively improve the reconstruction quality of the objects with complex structures.

Fig. 6. Experimental demonstration of phase imaging with low-bit speckle pattern. Results of reconstructing random smooth phase maps (left) and human face images (right) via DNN with patterns of different bit depths. The images in the middle column of each graph group are enlarged views of the areas selected by the yellow dotted box in the low-bit speckle patterns in the first column. The speckle patterns acquired at a distance of d2=60mm show lower local similarity and correspondingly lower reconstruction accuracy than the case of d2=5mm.

下载图片 查看所有图片

Note the worse imaging quality at a large distance between the diffuser and the camera sensor, as in the case of d2=60mm in Fig. 6. Even though the diffuser used has a very small diffusion angle (∼1°), the reconstructed image of the object is blurred, which differs somewhat from the result of imaging with the raw speckle measurement in Section 3.A. The overlap of speckles owing to severe geometric distortions will reduce the consistency of the binary patterns and tend to cause the patterns to change randomly. It seems to force the network to learn irregular variations, which will significantly reduce the accuracy of reconstruction in the absence of most of the intensity information. More specifically, the square areas at the same position in the low-bit patterns of different samples are enlarged and arranged in the middle column of each image group in Fig. 6. It shows the local distribution and the effect of pattern similarity on low-bit imaging when there is geometric distortion in the speckle field.

Further testing is about the generalizability of our model, which also determines whether DNN needs more classes of datasets for training. Accordingly, reconstruction of objects other than the class of the training set is performed. Figure 7 and Table 2 show the imaging performance of the network on samples in other different classes (ImageNet [49] and random phase) after being trained on the human face image dataset. Additionally, in both cases of imaging with binary images and raw measurements, experiments using diffraction patterns for imaging are arranged to visually reflect the role of the diffuser in low-bit imaging. For full bit depth, the performance of the DNN trained with speckle patterns on the testing samples from the learned class is almost the same as that of the DNN trained with diffraction patterns. However, the latter seems to be unable to well generalize the untouched classes that are quite different from the learned classes, such as simple random phase maps. For low bit depth, the reconstruction from the binary diffraction pattern almost fails. The results show the reasonable stability and generalizability of imaging with binarized speckle patterns and the compressibility brought by the diffuser. An unexpected result is the performance of SDVF on the testing samples; although its reconstruction accuracy on complicated objects is not satisfactory, it is suitable for recovering relatively simple and smooth phase objects even with binary patterns.

Fig. 7. Generalizability testing of the trained DNN in full-bit (10 bit measurement) and low-bit (1 bit binary pattern) imaging and comparison of the results of phase recovery under the three schemes: (i) imaging using diffraction patterns (without diffuser) via DNN; (ii) imaging using speckle patterns (with diffuser) via DNN; (iii) imaging using speckle patterns (with diffuser) via SDVF. All the data acquisitions adopt the same experimental configuration except for the diffuser settings. The distance between the diffuser and the camera sensor is fixed to 5 mm in both scheme (ii) and scheme (iii).

下载图片 查看所有图片

In order to know more about the compressibility of our method and how the amount of data influences the quality of phase imaging, quantitative analysis of redundant information is meaningful. We preliminarily use Shannon’s information theory [50] to simply calculate the information capacity of the image: Here n is the dimensionality of the image data or its total number of pixels, and m represents the level or the number of values that can be taken for each pixel. The analog-to-digital converter (ADC) in the camera sensor used in our experiment has a resolution of 10-bit, which provides a total of 1024 value levels. Therefore, the information capacity of a captured 512×512 single-channel speckle pattern and its binary version are 2,621,440 bits and 262,144 bits, respectively. It suggests that our method allows the acquired patterns to store the crucial information required for phase reconstruction with much less content than the raw data size and greatly saves the bandwidth of image acquisition and transmission.

Another analysis is about data sparseness. Note that the binarized speckle pattern contains a large number of zero-value pixels, which means that the experimental image data can be further encoded and compressed to save storage. A set of intensity thresholds is used for binarization to evaluate the impact of pattern sparseness on imaging quality. For the sake of convenience, the average intensity of the measurement is specified as the standard of the grayscale threshold (GT) and other thresholds are selected at equal intervals. Figure 8(a) shows the grayscale statistics of a speckle pattern captured by the camera sensor. The red dotted lines in the graph indicate the grayscale thresholds of interest, which are 0.5, 1.0 (average intensity), 1.5, 2.0, and 2.5 GT, respectively. Accordingly, Fig. 8(b) shows the result of binarization; the adjustment of the threshold could roughly change the distribution and amount of nonzero elements in the image. For the evaluation of pattern sparseness, a formula based on L1 norm and L2 norm introduced in Ref. [51] is applied: where n is the number of elements contained in the signal x. The calculated value is within the interval of [0,1] and becomes larger as the signal sparseness increases. As shown in Fig. 8(b), different grayscale thresholds lead to various sparseness of binary patterns and apparently influence the accuracy of phase recovery. Interestingly, our model seems to support the reconstruction of phase objects from fairly sparse binary patterns. When SP=0.9, there are only a few nonzero elements. Even so, reconstructed objects with slightly more complicated structures such as human face images can be easily recognized. However, if both the generalizability and the imaging quality of the model need to be considered, blindly focusing on the sparseness or the compressibility of the data may not be an appropriate decision. Also in Fig. 8(b), DNN is trained on the LFW Face dataset and used to reconstruct the image (Cat) in ImageNet. The generalization is not ideal when the pattern sparseness increases, and the reconstructed image becomes unrecognizable, as most of the details are lost. A statistical graph of reconstruction results over more testing samples is plotted in the inset of Fig. 8(a), which provides a simple reference for the trade-off between data compression and imaging quality. As can be seen, the quality of phase imaging as well as the generalizability of DNN will deteriorate as the sparseness of patterns increases. The appropriate intensity threshold for pattern binarization can be set to be slightly larger or near the average intensity of the measurement to obtain a better balance among imaging quality, data size, and model generalizability. In fact, the accuracy of phase recovery drops dramatically when the sparseness of patterns tends to both extremes (SP=0 and SP=1) as the features of grains are mostly destroyed.

Fig. 8. (a) Gray statistics of captured speckle images. Inset: graph of imaging accuracy and pattern sparseness at various binarization thresholds. (b) Result of reconstructing objects from binary patterns with different sparseness.

下载图片 查看所有图片

4. CONCLUSION

We have proposed a phase imaging approach by taking a single intensity pattern or its low-bit pattern based on deep learning. A thin diffuser (or random phase mask/plate) with a large memory effect range was employed as a physical encoder. With the support of DNN, the phase information of the object recorded in the distortion of the speckle field can then be almost completely extracted and restored. Due to the totally reference-free recording of the light field and the compactness brought by the combination of sensor and preconditioner, it suggests that our imaging system has the potential to be easily miniaturized compared to the existing phase imaging system based on interferometry.

Different from other intensity-dependent methods, accurate or redundant intensity measurements are nonessential for stable end-to-end reconstruction in our method. The experiments of recovering phase objects using full-bit pattern and low-bit pattern both show reasonable reconstruction accuracy, proving the high redundancy of the imaging data in our model. Furthermore, the compressibility of our model is verified by specific analysis on the information capacity and data sparsity of low-bit imaging. It is expected that in addition to the obvious advantages of reducing data transmission bandwidth and storage, this compressibility can also be employed at the optical acquisition side to reduce the cost of sensor hardware and equipment.

The preconditioner can be alternative. The diffuser is used in our model because it naturally provides abundant features for intensity measurement. Nevertheless, this does not mean that diffuser is the only option, for example, a well-designed grating may be also applicable.