穆勒矩阵成像椭偏仪误差源的简化分析方法

孟泽江; 李思坤; 王向朝; 步扬; 戴凤钊; 杨朝兴

doi:doi:10.3788/AOS201939.0911002

光学学报, 2019, 39 (9): 0911002, 网络出版: 2019-09-09

穆勒矩阵成像椭偏仪误差源的简化分析方法下载： 965次

Simplified Analytical Method for Error Sources in Mueller Matrix Imaging Polarimeter

论文大纲

孟泽江 ^1,2李思坤 ^1,2,*王向朝 ^1,2,**步扬 ^1,2戴凤钊 ^1,2杨朝兴 ^1,2

作者单位

¹ 中国科学院上海光学精密机械研究所信息光学与光电技术实验室, 上海 201800

² 中国科学院大学材料与光电研究中心, 北京 100049

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

针对穆勒矩阵成像椭偏仪的系统误差源提出一种简化分析方法,将光强曲线的理想傅里叶级数系数组与实际系数组进行近似匹配,建立穆勒矩阵测量误差与误差源参数之间的线性模型。针对解析式复杂的随机方位角误差,从统计学角度提出了一种等效噪声模型以分析其对测量结果的影响。采用上述简化方法系统分析了椭偏仪的6种系统误差源和2种随机误差源对穆勒矩阵测量结果的影响,并以一个典型光刻投影物镜的穆勒光瞳为检测对象,进行了检测仿真。仿真结果验证了所提方法分析的准确性。

Abstract

Aim

ing at systematic error sources in a Mueller matrix imaging polarimeter, we propose a simplified analytical method based on the approximate matching of the ideal coefficients of Fourier series of the intensity curve with the real ones. By using the method, a linear relationship between the deviation of the Mueller matrix and the parameter of the error source is built. The analytical expression for random error caused by the azimuthal angle is complex, so an equivalent noise model is proposed to characterize the impact of misalignment from the view of statistics. Based on the simplified models above, we conduct a comprehensive analysis for the measured Mueller matrices influenced by six kinds of systematic error sources and two kinds of random error sources. The simulation for the measurement of a typical Mueller pupil of the lithographic projector is performed. The results verify the accuracy of the proposed method.

1 引言

光刻机是极大规模集成电路制造的核心装备。为提升成像分辨率,主流的深紫外光刻机均采用偏振光照明和超大数值孔径(NA=1.35)投影物镜。这使得偏振效应对光刻成像的影响尤为明显^[1]。偏振像差反映了光学系统对入射光振幅、相位和偏振态的改变。这一改变量随入射偏振态,以及光束倾斜角或频域出瞳点的变化而变化^[2-3]。若用琼斯矢量或斯托克斯矢量表征入射偏振光,则偏振像差可表示为在出瞳面上分布的琼斯矩阵函数或穆勒矩阵函数,即琼斯光瞳或穆勒光瞳^[4]。投影物镜的偏振像差会降低光刻成像质量^[5-6],因此需要对其进行高精度的测量和有效的补偿。基于双旋波片法的穆勒矩阵成像椭偏仪^[7]是测量光学系统偏振像差的典型装置。在实际测量过程中,非理想的偏振片和波片、偏振元件的方位角误差,以及图像传感器的噪声均会影响穆勒光瞳的测量精度。光刻成像系统对像差的检测和控制有极为严苛的要求。为尽可能地减小测量误差,首先需要建立椭偏仪各类误差源对测量结果影响的理论模型,且该模型应具有简单清晰的形式,可用于进行综合误差评定、误差源指标分解、元件误差标定和补偿。

关于穆勒矩阵成像椭偏仪的误差分析已有多项研究。关于椭偏仪的系统误差,Goldstein等^[8]和Bhattacharyya等^[9]采用傅里叶级数系数分析法推导了实测穆勒矩阵各元素与受误差源影响的光强曲线傅里叶系数之间的关系式,并分析了波片偏振衰减误差、相位延迟误差和方位角误差的影响。该方法是严格方法,适用于任何范围的误差分析,但该方法的表达式形式复杂,而且以傅里叶系数为自变量,无法直接反映误差源参数和原始穆勒矩阵元素的作用。Nee^[10]和Savenkov等^[11]基于起偏和检偏端分离的原理,定义了起偏和检偏斯托克斯矢量形式的误差源参数,并分别推导了不同形式的穆勒矩阵误差表达式,但所得表达式的自变量均为综合的矢量误差源,无法直接反映每一种原始误差源带来的影响。Broch等^[12-13]利用穆勒矩阵各元素对光强的傅里叶系数进行求导,结合傅里叶系数关于误差源参数的泰勒展开式,提出了穆勒矩阵误差的一阶近似和二阶近似模型,分析了偏振片和波片的方位角、偏振衰减和相位延迟对误差的影响。该模型的表达式简单,但采用了求导方法,因此只适用于所有穆勒矩阵元素均变化较小的情况。

针对现有系统误差分析方法存在的问题,本文提出一种系统误差源的简化分析方法:令光强曲线原始形式和实测形式的傅里叶系数组逐项相等,舍弃或近似处理使方程组无解的超定项,通过解方程得到穆勒矩阵误差与误差源参数和原始穆勒矩阵的线性表达式。与同类方法相比,所得表达式形式简单,且适用于穆勒矩阵元素一般变化的情况。

关于椭偏仪的随机误差源,Anna等^[14]基于方差模型分析了高斯噪声和散射噪声的影响。此类光强形式随机误差的传递过程具有形式简单的解析表达式。但对于随机方位角误差而言,其传递过程难以通过解析式表达。本文对此类误差源进行了讨论,并从统计角度提出一种等效噪声模型以分析其影响。

基于上述简化方法,全面分析了穆勒矩阵成像椭偏仪的6种系统误差源和2种随机误差源对穆勒矩阵测量的影响,并以一个典型光刻投影物镜的琼斯光瞳为检测对象,在含误差的一般情况下进行了检测仿真,结果验证了本文方法的准确性。

2 基本原理

2.1 穆勒矩阵成像椭偏仪的测量原理

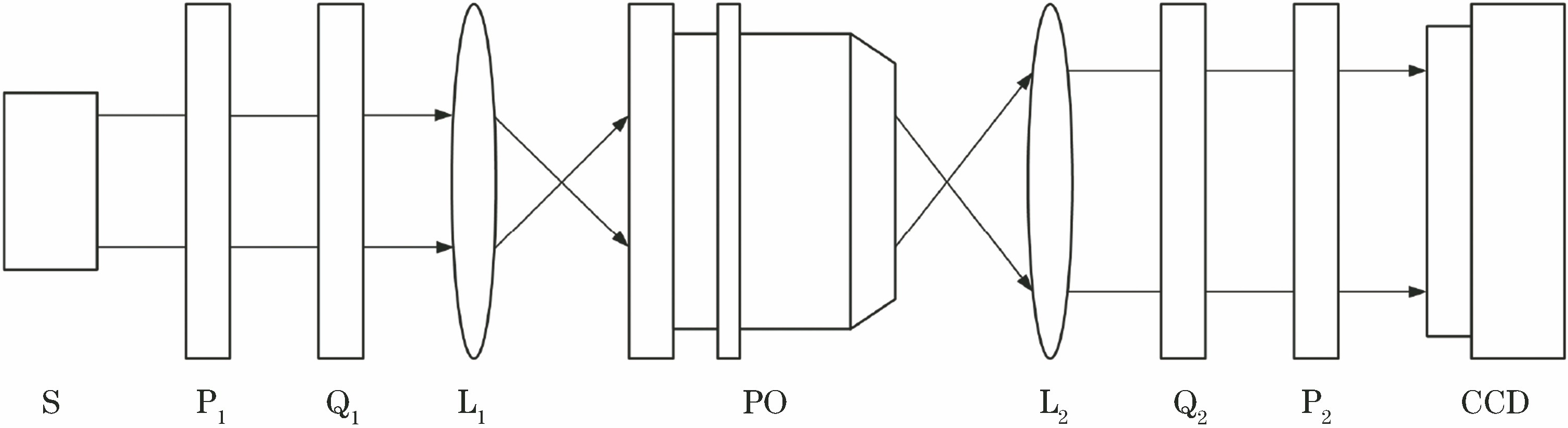
用于偏振像差检测的穆勒矩阵成像椭偏仪的系统结构如图1所示^[15],由光源S、偏振片P₁/P₂、1/4波片Q₁/Q₂、聚焦/准直投镜L₁/L₂、投影物镜PO和CCD构成。L₁和L₂的作用是对PO的频域光瞳进行傅里叶变换,从而使CCD的单个像素点对应PO的单个光瞳点。在测量时,Q₁和Q₂按一定的角度比旋转,以产生不同的入射偏振态和检测相应的出射偏振态,通过求解所得的线性方程计算相应光瞳点的穆勒矩阵。

对于图像传感器的某一像素,测得的光强I与Q₁方位角θ的关系为

I (θ) = [\begin{array}{l} 1 & 0 & 0 & 0 \end{array}] P_{2} Q_{2} (kθ) M Q_{1} (θ) P_{1} S_{0}, (1)

式中:M为被测穆勒矩阵;S₀为光源出射光的斯托克斯矢量,一般可视为非偏振光,即S₀=[1 0 0 0]^T;P₁、Q₁、Q₂、P₂依次为相应偏振元件的穆勒矩阵;k为Q₂和Q₁旋转角的比例,一般取5。利用多个I值求解M有两种方式,分别适用于系统误差源和随机误差源的分析。

图 1. 用于偏振像差检测的穆勒矩阵成像椭偏仪的结构图

Fig. 1. Structure of Mueller matrix imaging polarimeter for measuring polarization aberration

下载图片查看所有图片

第一种方法采用傅里叶级数拟合多个光强点分布。I与θ的关系可表示为

I (θ) = a_{0} + \overset{12}{\sum_{l = 1}} a_{2 l - 1} \cos [T_{l} (k) θ] + a_{2 l} \sin [T_{l} (k) θ], (2)

式中:T_l(k)是第l正弦项或余弦项对应的角度倍数,与k的取值有关,l的取值范围为1~12;a₀~a₂₄表示常数项,以及各正弦项和余弦项的系数,即傅里叶级数的系数(简称为傅里叶系数)。这24个傅里叶系数均为穆勒矩阵M各元素的线性组合,若写成方程组的形式,在无误差时共有16个线性无关的方程,可用于求解M的16个元素。

第二种方法采用最小二乘法求取多个光强值与穆勒矩阵各元素构成的超定方程组,即

I = C vec (M) = [\begin{array}{l} K (θ_{1}) \\ K (θ_{2}) \\ ︙ \\ K (θ_{n}) \end{array}] [\begin{array}{l} m_{11} \\ m_{21} \\ ︙ \\ m_{44} \end{array}], (3)

式中:I是n次测量所得的光强值构成的列向量;C是灵敏度系数矩阵,由n个系数行向量K(θ₁)~K(θ_n)构成,每个K向量可由(1)式计算;θ₁~θ_n是n次测量Q₁的方位角,一般为等间隔角;vec是向量化运算符,表示使M各元素m_ij按列堆叠。通过最小二乘法求解M,即

vec (M) = SI, S = (C^{T} {C)}^{- 1} C^{T}, (4)

式中:S是灵敏度系数矩阵C的最小二乘逆矩阵。

所有光瞳点上的穆勒矩阵均采用相同的方法求解,而且暂不考虑各元件误差空间分布的不均匀性,以及非理想聚焦/准直投镜L₁和L₂的影响,因此后续的理论分析均基于单个穆勒矩阵的测量,且不对椭偏仪和成像椭偏仪加以区分。

2.2 穆勒矩阵成像椭偏仪的误差源

表1给出了穆勒矩阵成像椭偏仪的主要误差源,共有6种系统误差源和2种随机误差源^[15]。在实际测量过程中,非理想的偏振元件、偏振元件的方位角误差,以及图像传感器的噪声均会影响穆勒光瞳的测量精度。

表 1. 穆勒矩阵成像椭偏仪的误差源

Table 1. Error sources in Mueller matrix imaging polarimeter

Error type	Element	Error parameter	Typical value
	Quarter-wave plates	Retardance error δ	0.001π
	Q₁, Q₂	Diattenuation error ε	0.01
Systematic		Azimuthal angle error Δθ /(°)	0.1
	Polarizers	Diattenuation error ε	0.01
	P₁, P₂	Retardance error δ	0.001π
		Azimuthal angle error Δθ /(°)	0.1
Random	Image sensor CCD	Noise σ (ΔI)	0.003
(normal distribution)	Q₁, Q₂	Azimuthal angle error σ (Δθ_R) /(°)	0.1

查看所有表

系统误差主要来自非理想非对准的偏振片P₁、P₂和1/4波片Q₁、Q₂。对于这两种元件,需考虑其偏振衰减误差ε、相位延迟误差δ和方位角误差Δθ,其含误差的穆勒矩阵分别为

\begin{array}{l} P (θ, ε, δ, Δ θ) = R (- θ - Δ θ) [\begin{array}{l} \frac{1 + ε^{2}}{2} & \frac{1 - ε^{2}}{2} & 0 & 0 \\ \frac{1 - ε^{2}}{2} & \frac{1 + ε^{2}}{2} & 0 & 0 \\ 0 & 0 & ε \cos δ & - ε \sin δ \\ 0 & 0 & ε \sin δ & ε \cos δ \end{array}] R (θ + Δ θ), (5) \\ Q (θ, ε, δ, Δ θ) = R (- θ - Δ θ) [\begin{array}{l} 1 - \frac{2 ε - ε^{2}}{2} & - \frac{2 ε - ε^{2}}{2} & 0 & 0 \\ - \frac{2 ε - ε^{2}}{2} & 1 - \frac{2 ε - ε^{2}}{2} & 0 & 0 \\ 0 & 0 & (ε - 1) \sin δ & (ε - 1) \cos δ \\ 0 & 0 & (1 - ε) \cos δ & (ε - 1) \sin δ \end{array}] R (θ + Δ θ), (6) \end{array}

式中:R(θ)表示坐标轴旋转的穆勒矩阵,表达式为

R (θ) = [\begin{array}{l} 1 & 0 & 0 & 0 \\ 0 & \cos (2 θ) & \sin (2 θ) & 0 \\ 0 & - \sin (2 θ) & \cos (2 θ) & 0 \\ 0 & 0 & 0 & 1 \end{array}] 。 (7)

以(5)式和(6)式的含误差元件模型作为后续误差分析公式推导的基础。表1给出了δ、ε和Δθ这三种误差的典型值。为简化并方便比较不同元件同类误差的影响,假设起偏和检偏元件的误差参数相等或只是正负号不同,偏振片和1/4波片的误差参数相等。

随机误差主要来自图像传感器的噪声。图像传感器的噪声主要来源于散粒噪声,散粒噪声引起的光强误差ΔI可近似看作正态分布。此外,1/4波片Q₁和Q₂在测量过程中多次旋转,其方位角误差除了与系统误差Δθ有关外,还与随机误差Δθ_R有关。虽然ΔI和Δθ_R的期望均为0,但两者的方差到各个穆勒矩阵元素方差的传递系数并不相同,因此仍有进行理论分析和建模的必要。

3 系统误差源的简化分析方法

3.1 波片的相位延迟误差分析

位于起偏和检偏端的1/4波片Q₁和Q₂通常采用相同元件。为从数量级上分析这类误差的影响,并与其他误差进行比较,假设Q₁和Q₂的相位延迟误差δ大小相等且符号相同。在相位延迟误差的干扰下,实测光强曲线函数I'(θ)可表示为

I' (θ) = {[\begin{array}{l} a_{0} (M, δ) \\ a_{1} (M, δ) \\ a_{2} (M, δ) \\ ︙ \\ a_{23} (M, δ) \\ a_{24} (M, δ) \end{array}]}^{T} [\begin{array}{l} 1 \\ \cos [T_{1} (k) θ] \\ \sin [T_{1} (k) θ] \\ ︙ \\ \cos [T_{12} (k) θ] \\ \sin [T_{12} (k) θ] \end{array}], (8)

式中:M代表原始的被测的穆勒矩阵,即每一个傅里叶系数均为M各元素的线性组合,且在误差源的干扰下这些线性组合的系数与δ有关。(8)式表示δ到傅里叶系数a₀~a₂₄再到实测光强分布I'的正向传递过程。穆勒矩阵的逆向求解过程与之对称,即先将I'分解为各傅里叶系数,再在理想无误差的条件下求解测得的穆勒矩阵M',该过程可表示为

I' (θ) = {[\begin{array}{l} a_{0} (M') \\ a_{1} (M') \\ a_{2} (M') \\ ︙ \\ a_{23} (M') \\ a_{24} (M') \end{array}]}^{T} [\begin{array}{l} 1 \\ \cos [T_{1} (k) θ] \\ \sin [T_{1} (k) θ] \\ ︙ \\ \cos [T_{12} (k) θ] \\ \sin [T_{12} (k) θ] \end{array}] 。 (9)

在实际测量过程中,M和δ的正向传递与M'的逆向求解均基于相等的实测光强点I'₁,I'₂,…,I'_n。考虑一个更充分的条件:a₀(M, δ)=a₀(M'),a₁(M, δ)=a₁(M'),…,a₂₄(M, δ)=a₂₄(M'),即正向逆向过程对应的傅里叶系数一一相等。在这种条件下,可以消去傅里叶系数变量,联立并求解25个方程从而直接建立M'与M和δ的关系。但是,这一设想存在两个问题:首先,一般情况下所得方程为超定方程组,无严格解;其次,即使方程组有唯一解,M'的表达式复杂,无法直观看出误差的传递规律。

为解决以上问题,采用一种非严格一阶近似的傅里叶系数匹配方法以得到形式简单且较为准确的误差模型。对于傅里叶系数一一匹配得到的原始方程组,一方面通过舍弃理想傅里叶系数为零的方程或合并两两矛盾的方程使方程组有唯一解,另一方面对误差源只考虑相应参数的一次项,以简化误差模型的公式表达。

令s₁=sin δ,c₁=cos δ,a₀(M, δ)~a₂₄(M, δ)的表达式如表2第3列所示。将其中s₁的二次项置0,同时令c₁=1,可得到第4列的简化表达式。

表 2. 含波片相位延迟误差的光强傅里叶系数

Table 2. Fourier coefficients of light intensity influenced by delay errorof retarder

Order	Term	Coefficient of Fourier series	Approximate coefficient
0	1	m₁₁/4+(1-s₁) (m₁₂+m₂₁)/8+(1-s₁)²m₂₂/16	m₁₁/4+(1-s₁) (m₁₂+m₂₁)/8+(1-2s₁) m₂₂/16
1	cos(2θ)	0	0
2	sin(2θ)	-c₁m₁₄/4-c₁ (1-s₁) m₂₄/8	-m₁₄/4-(1-s₁) m₂₄/8
3	cos(2kθ)	0	0
4	sin(2kθ)	c₁m₄₁/4+c₁ (1-s₁) m₄₂/8	m₄₁/4+(1-s₁) m₄₂/8
5	cos[2(1+k)θ]	c₁₂m₄₄/8	m₄₄/8
6	sin[2(1+k)θ]	0	0
7	cos[2(1-k)θ]	-c₁₂m₄₄/8	-m₄₄/8
8	sin[2(1-k)θ]	0	0
9	cos(4θ)	(1-s₁₂) m₂₂/16+(1+s₁) m₁₂/8	m₂₂/16+(1+s₁) m₁₂/8
10	sin(4θ)	(1-s₁₂) m₂₃/16+(1+s₁) m₁₃/8	m₂₃/16+(1+s₁) m₁₃/8
11	cos(4kθ)	(1-s₁₂) m₂₂/16+(1+s₁) m₂₁/8	m₂₂/16+(1+s₁) m₂₁/8
12	sin(4kθ)	(1-s₁₂) m₃₂/16+(1+s₁) m₃₁/8	m₃₂/16+(1+s₁) m₃₁/8
13	cos[4(1+k)θ]	(1+s₁)² (m₂₂-m₃₃)/32	(1+2s₁) (m₂₂-m₃₃)/32
14	sin[4(1+k)θ]	(1+s₁)² (m₂₃+m₃₂)/32	(1+2s₁) (m₂₃+m₃₂)/32
15	cos[4(1-k)θ]	(1+s₁)² (m₂₂+m₃₃)/32	(1+2s₁) (m₂₂+m₃₃)/32
16	sin[4(1-k)θ]	(1+s₁)² (m₂₃-m₃₂)/32	(1+2s₁) (m₂₃-m₃₂)/32
17	cos[2(1+2k)θ]	c₁ (1+s₁) m₃₄/16	(1+s₁) m₃₄/16
18	sin[2(1+2k)θ]	-c₁ (1+s₁) m₂₄/16	-(1+s₁) m₂₄/16
19	cos[2(1-2k)θ]	-c₁ (1+s₁) m₃₄/16	-(1+s₁) m₃₄/16
20	sin[2(1-2k)θ]	-c₁ (1+s₁) m₂₄/16	-(1+s₁) m₂₄/16
21	cos[2(2+k)θ]	-c₁ (1+s₁) m₄₃/16	-(1+s₁) m₄₃/16
22	sin[2(2+k)θ]	c₁ (1+s₁) m₄₂/16	(1+s₁) m₄₂/16
23	cos[2(2-k)θ]	c₁ (1+s₁) m₄₃/16	(1+s₁) m₄₃/16
24	sin[2(2-k)θ]	-c₁ (1+s₁) m₄₂/16	-(1+s₁) m₄₂/16

查看所有表

在一阶近似的条件下,只有穆勒矩阵的m₄₄元素对应的系数不受此类误差影响,而其他系数在δ的影响下一般变为自身或自身一部分项的1+s₁倍。需要注意的是,穆勒矩阵各元素的大小往往有较大差异。对于所研究的小像差系统,如光刻投影物镜系统,所有光瞳点的穆勒矩阵接近单位矩阵,即只有主对角线元素m₁₁、m₂₂、m₃₃、m₄₄接近1,而其他元素至少要小一个数量级。在这种情况下,若某一傅里叶系数包含s₁与主对角线元素的乘积,且该系数可用于求解非主对角线元素(表2中标为粗体格式的元素),则其受δ的影响较大。表2中的a₀是符合这一条件的傅里叶系数,其作用是与a₉和a₁₁联立求解m₁₂和m₂₁。m₁₂和m₂₁本身的值均远小于m_22,但相应的误差却包含m₂₂与s₁的乘积,因此s₁误差在传递到m₁₂和m₂₁误差的过程中被明显放大。

将表2第4列中M各元素和s₁分别替换为M'各元素和0,通过傅里叶系数一一匹配列出并求解方程组。由于δ误差只引起傅里叶系数的相对变化,因此方程组恰好有唯一解,得到波片相位延迟误差影响下的穆勒矩阵误差ΔM_q-_δ的表达式为

Δ M_{q ⁃ δ} = [\begin{array}{l} - m_{12} - m_{21} & m_{12} - m_{22} & m_{13} - m_{23} & - m_{24} \\ m_{21} - m_{22} & 2 m_{22} & 2 m_{23} & m_{24} \\ m_{31} - m_{32} & 2 m_{32} & 2 m_{33} & m_{34} \\ - m_{42} & m_{42} & m_{43} & 0 \end{array}] s_{1} 。 (10)

(10)为形式简单的M各元素的线性组合与s₁的乘积。从(10)式可直观看出,系统误差源引入的穆勒矩阵误差与原始穆勒矩阵紧密相关。穆勒矩阵元素误差Δm₁₂和Δm₂₁的系数包含主对角线元素m₂₂,说明δ会对m₁₂和m₂₁产生较大影响,但对其余元素只引起不明显的相对变化。

3.2 波片的偏振衰减误差和方位角误差分析

对于1/4波片Q₁和Q₂的偏振衰减误差ε和方位角误差Δθ,同样采用3.1节叙述的简化分析方法推导误差传递公式。首先令s₂=ε,s₃=sin(2Δθ),采用一阶近似分别得到δ和Δθ对应的傅里叶系数,如表3的第3列和第4列所示。

从表3可以看出,ε会使所有傅里叶系数发生改变,且会引起各傅里叶系数相对于自身的变化。Δθ不会改变a₀、a₂、a₄、a₅、a₇、a₁₅、a₁₆,但会使其他傅里叶系数发生与对偶系数成比例的变化,而非相对于自身的变化,如a'₉=a₉+2s₃a₁₀,a'₁₀=a₁₀-2s₃a₉。

和3.1节讨论的δ不同,无论是ε还是Δθ,严格匹配傅里叶系数所得的方程组均无解。分析其原因:1)原本为0的a₁、a₃、a₆、a₈系数在误差源影响下变为非零表达式,使求解ε或Δθ的方程组多出4个或3个约束条件;2)对于ε或Δθ而言,原本只差正负号的4对系数a₁₇和a₁₉、a₁₈和a₂₀、a₂₁和a₂₃、a₂₂和a₂₄在误差源影响下均加上同一个量或加减不同的量,使含误差的4对系数等式两两矛盾。表3中的粗体格式元素为使方程组从唯一解变为无解的部分。

表 3. 含波片偏振衰减和方位角误差的光强傅里叶系数

Table 3. Fourier coefficients of light intensity influenced by diattenuation and azimuthal-angle error of retarder

Order	Term	Approximate coefficient (ε)	Approximate coefficient (θ)
0	1	(1-2s₂) (m₁₁/4+(m₁₂+m₂₁)/8+m₂₂/16)	m₁₁/4+(m₁₂+m₂₁)/8+m₂₂/16
1	cos(2θ)	s₂ (m₁₁/4+m₁₂/4+m₂₁/8+m₂₂/8)	-s₃ (m₁₄/4+m₂₄/8)
2	sin(2θ)	-(m₁₄/4+m₂₄/8)+s₂ (m₁₄/2+m₂₄/4+m₁₃/4+m₂₃/8)	-(m₁₄/4+m₂₄/8)
3	cos(2kθ)	s₂ (m₁₁/4+m₂₁/4+m₁₂/8+m₂₂/8)	s₃ (m₄₁/4+m₄₂/8)
4	sin(2kθ)	(m₄₁/4+m₄₂/8)-s₂ (m₄₁/2+m₄₂/4-m₃₁/4-m₃₂/8)	(m₄₁/4+m₄₂/8)
5	cos[2(1+k)θ]	m₄₄/8-s₂ (m₄₄/4-m₃₄/8+m₄₃/8)	m₄₄/8
6	sin[2(1+k)θ]	-s₂ (m₁₄/8+m₂₄/8-m₄₁/8-m₄₂/8)	-s₃m₄₄/4
7	cos[2(1-k)θ]	-m₄₄/8+s₂ (m₄₄/4-m₃₄/8+m₄₃/8)	-m₄₄/8
8	sin[2(1-k)θ]	-s₂ (m₁₄/8+m₂₄/8+m₄₁/8+m₄₂/8)	0
9	cos(4θ)	(1-2s₂) (m₁₂/8+m₂₂/16)	(m₁₂/8+m₂₂/16)+s₃ (m₁₃/4+m₂₃/8)
10	sin(4θ)	(1-2s₂) (m₁₃/8+m₂₃/16)	(m₁₃/8+m₂₃/16)-s₃ (m₁₂/4+ $\overset{/}{m_{22}}$ )
11	cos(4kθ)	(1-2s₂) (m₂₁/8+m₂₂/16)	(m₂₁/8+m₂₂/16)+s₃ (m₃₁/4+m₃₂/8)
12	sin(4kθ)	(1-2s₂) (m₃₁/8+m₃₂/16)	(m₃₁/8+m₃₂/16)-s₃ (m₂₁/4+ $\overset{/}{m_{22}}$ )
13	cos[4(1+k)θ]	(1-2s₂) (m₂₂-m₃₃)/32	(m₂₂-m₃₃)/32+s₃ (m₂₃+m₃₂)/8
14	sin[4(1+k)θ]	(1-2s₂) (m₂₃+m₃₂)/32	(m₂₃+m₃₂)/32-s₃ (m₂₂-m₃₃)/8
15	cos[4(1-k)θ]	(1-2s₂) (m₂₂+m₃₃)/32	(m₂₂+m₃₃)/32
16	sin[4(1-k)θ]	(1-2s₂) (m₂₃-m₃₂)/32	(m₂₃-m₃₂)/32
17	cos[2(1+2k)θ]	m₃₄/16-s₂ (m₃₄/8+ $\overset{/}{m_{33}}$ -m₂₁/16-m₂₂/16)	m₃₄/16-3s₃m₂₄/16
18	sin[2(1+2k)θ]	-m₂₄/16+s₂ (m₂₄/8+m₂₃/16+m₃₁/16+m₃₂/16)	-m₂₄/16-3s₃m₃₄/16
19	cos[2(1-2k)θ]	-m₃₄/16+s₂ (m₃₄/8+ $\overset{/}{m_{33}}$ +m₂₁/16+m₂₂/16)	-m₃₄/16+s₃m₂₄/16
20	sin[2(1-2k)θ]	-m₂₄/16+s₂ (m₂₄/8+m₂₃/16-m₃₁/16-m₃₂/16)	-m₂₄/16-s₃m₃₄/16
21	cos[2(2+k)θ]	-m₄₃/16+s₂ (m₄₃/8- $\overset{/}{m_{33}}$ +m₁₂/16+m₂₂/16)	-m₄₃/16+3s₃m₄₂/16
22	sin[2(2+k)θ]	m₄₂/16-s₂ (m₄₂/8-m₃₂/16-m₁₃/16-m₂₃/16)	m₄₂/16+3s₃m₄₃/16
23	cos[2(2-k)θ]	m₄₃/16-s₂ (m₄₃/8- $\overset{/}{m_{33}}$ -m₁₂/16-m₂₂/16)	m₄₃/16-s₃m₄₂/16
24	sin[2(2-k)θ]	-m₄₂/16+s₂ (m₄₂/8-m₃₂/16+m₁₃/16+m₂₃/16)	-m₄₂/16-s₃m₄₃/16

查看所有表

使用3.1节所述的非严格的匹配方法,首先舍弃新增的a₁、a₃、a₆、a₈误差表达式对应的方程。其次,对于ε引入的改变,将4对系数a₁₇和a₁₉、a₁₈和a₂₀、a₂₁和a₂₃、a₂₂和a₂₄的表达式中含s₂且两两互为正负的部分予以保留、含s₂且两两相等的部分予以舍弃;对于Δθ引入的改变,将4对系数的表达式中的含-3s₃和s₃项分别平均化为-2s₃和-2s₃项、含3s₃和-s₃项分别平均化为2s₃和2s₃项。求解近似匹配后得到的方程组,所得波片偏振衰减和方位角误差影响下的穆勒矩阵误差ΔM_q-_ε 和ΔM_q-_θ的表达式分别为

\begin{array}{l} Δ M_{q ⁃ ε} = - [\begin{array}{l} 2 m_{11} & 2 m_{12} & 2 m_{13} & m_{13} + 2 m_{14} \\ 2 m_{21} & 2 m_{22} & 2 m_{23} & m_{23} + 2 m_{24} \\ 2 m_{31} & 2 m_{32} & 2 m_{33} & m_{33} + 2 m_{34} \\ - m_{31} + 2 m_{41} & - m_{32} + 2 m_{42} & - m_{33} + 2 m_{43} & - m_{34} + m_{43} + 2 m_{44} \end{array}] s_{2}, (11) \\ Δ M_{q ⁃ θ} = [\begin{array}{l} - m_{13} - m_{31} & 2 m_{13} - m_{32} & - 2 m_{12} - m_{33} & - m_{34} \\ - m_{23} + 2 m_{31} & 2 m_{23} + 2 m_{32} & - 2 m_{22} + 2 m_{33} & 2 m_{34} \\ - 2 m_{21} - m_{33} & - 2 m_{22} + 2 m_{33} & - 2 m_{23} - 2 m_{32} & - 2 m_{24} \\ - m_{43} & 2 m_{43} & - 2 m_{42} & 0 \end{array}] s_{3} 。 (12) \end{array}

表3中反映偏振衰减误差ε的第3列系数共有11项包含s₂与主对角线元素的乘积,但只有标为下划线格式的4项(两两互为正负,实际只有两项有效)会使穆勒矩阵非主对角线元素误差Δm₃₄和Δm₄₃的系数包含主对角线元素m₃₃,即s₂误差在传递到m₃₄和m₄₃误差的过程中会被明显放大。从(11)式也可以看出m₃₄和m₄₃受s₂影响较大。

表3中反映方位角误差Δθ的第4列系数只有3项包含s₃与主对角线元素的乘积,其中标为下划线格式的2项会使Δm₁₃和Δm₃₁的系数包含主对角线元素m₃₃,从而明显放大s₃的影响。从(12)式也可以看出,m₁₃和m₃₁受s₃影响较大。

对于1/4波片,三种误差源造成的穆勒矩阵误差均与原始穆勒矩阵相关,且误差在同一数量级。在这三种情况下,原始穆勒矩阵分别有两个非主对角线元素(m₁₂和m₂₁、m₃₄和m₄₃、m₁₃和m₃₁)受误差源影响较大,其原因是误差传递系数包含接近1的主对角线元素。

3.3 偏振片的三种系统误差分析

对于偏振片P₁和P₂的三种系统误差,同样采用3.1节叙述的简化分析方法推导误差传递公式。由偏振片方位角误差Δθ、偏振衰减误差ε和相位延迟误差δ引起的穆勒矩阵误差ΔM_p-_θ、ΔM_p-_ε和ΔM_p-_δ的表达式分别为

Δ M_{p ⁃ θ} = [\begin{array}{l} m_{13} + m_{31} & - m_{13} + m_{32} & m_{12} + m_{33} & m_{34} \\ m_{23} - m_{31} & - m_{23} - m_{32} & m_{22} - m_{33} & - m_{34} \\ m_{21} + m_{33} & m_{22} - m_{33} & m_{23} + m_{32} & m_{24} \\ m_{43} & - m_{43} & m_{42} & 0 \end{array}] s_{3}, (13)

\begin{array}{l} Δ M_{p ⁃ ε} = - [\begin{array}{l} - m_{11} & 0 & 0 & 0 \\ 0 & m_{22} & m_{23} & m_{24} \\ 0 & m_{32} & m_{33} & m_{34} \\ 0 & m_{42} & m_{43} & m_{44} \end{array}] 2 s_{2}^{2}, (14) \\ Δ M_{p ⁃ δ} = [\begin{array}{l} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}] s_{1}, (15) \end{array}

式中:s₃、s₂、s₁的定义与3.1和3.2节相同。三种误差的数量级依次递减:ΔM_p-_θ与s₃成正比,ΔM_p-_ε 只包含s₂的二次项,而ΔM_p-_δ恒为0。

对于Δθ,ΔM_p-_θ表达式的形式与ΔM_q-_θ类似,将ΔM_q-_θ右下的3×3子块用A表示, ΔM_p-_θ右下子块用B表示,二者满足A=-2B,即在两者共同作用下,M右下3×3子块的元素误差会以1∶2的比例相互抵消。对于ε,由于偏振片的起偏过程是从非偏振光中按两个正交偏振基以1∶ε²的强度比产生线偏振光,故所得线偏振光的斯托克斯参量不包含ε的一次项。同理,偏振片的检偏过程最终得到的ΔM_p-_ε只包含s₃的二次项。对于δ,由于非偏振光可分解为两个相位无关或相位随机的正交偏振基,故起偏偏振片的相位延迟误差不会起任何作用。同理,偏振片的检偏过程最终得到的ΔM_p-_δ恒为0。因此,一般只需考虑偏振片方位角误差Δθ的影响,且该影响整体小于1/4波片Δθ的影响。

4 随机误差源的简化模型

4.1 图像传感器噪声分析

除了傅里叶系数分析方法,通过(3)式的光强方程组可以看出,随机误差源分为影响光强向量I或影响灵敏度系数矩阵C两类。对于随机光强形式的误差源ΔI,根据(4)式,ΔM与ΔI具有简单的线性传递关系,且传递系数矩阵S与原始穆勒矩阵M无关。随机误差的期望可认为是0,一般用方差或标准差表示误差源参数。若<·>表示统计平均,则ΔI误差协方差的传递表达式为

< vec {(Δ M)}_{i} vec {(Δ M)}_{j} > = \sum_{u, v} S_{i, u} S_{j, v} < Δ I_{u} Δ I_{v} >, (16)

式中:u和v是光强误差向量ΔI的下标,范围是1~n,n为测量次数;i和j是穆勒矩阵误差向量vec(ΔM)的下标,范围是1~16。若ΔI来源于图像传感器的噪声,可认为图像传感器某像素的不同次光强测量相互独立,且每一次测量误差的方差均等于传感器整体噪声的方差,即<Δ $I_{u}^{2}$ >=σ²(ΔI),且<ΔI_uΔI_v>_u_≠_v=0。

令r₁=σ(ΔI),则在图像传感器噪声的影响下,穆勒矩阵误差ΔM_I标准差的表达式为

σ [vec (Δ M_{I})] = \sqrt[]{diag (S^{T} S)} r_{1}, (17)

式中:diag运算表示对矩阵只保留主对角线上的元素。(17)式表明,M每一个元素误差的标准差均只与误差源参数r₁线性相关,而线性系数的分布则只与测量方案有关。

4.2 波片的随机角度误差分析

对于系统误差,除了对正向过程和逆向过程相应的傅里叶系数表达式进行分析外,还可直接对比正向和逆向过程相应的光强方程组,即将(3)式写为

(C + Δ C) vec (M) = I' = C vec (M + Δ M), (18)

式中:系统误差源首先传递到灵敏度系数矩阵误差ΔC中,再引起穆勒矩阵误差ΔM。ΔC到ΔM的传递关系为

vec (Δ M) = (S Δ C) vec (M) 。 (19)

与基于傅里叶系数匹配法所得的公式相比,SΔC包含了误差源的参数和对M的线性变换。虽然傅里叶系数匹配法在分析影响C的系统误差源时非常直观,但该方法无法分析影响C的随机误差源。这是因为:随机误差源产生的影响无法以解析的形式代入傅里叶级数表示的光强曲线中。如果采用传递矩阵法,SΔC与影响C的误差(如方位角误差)的关系式极为复杂。对于随机方位角误差等特殊的误差,可将这种影响C的随机误差源等效转化为影响I的误差源,并得到近似的统计模型。

改变(19)式变量的结合顺序,可得

vec (Δ M) = S [Δ C vec (M)] = S Δ I_{eq} 。 (20)

如果ΔC与vec(M)的乘积ΔI_eq期望为0,且方差为不随M变化的固定值,则ΔI_eq可等效成传感器噪声。为证明随机方位角误差近似满足上述条件,令s₃₁=sin(2Δθ_R)和s₃₂=sin(2Δθ_R)分别代表两个1/4波片Q₁和Q₂方位角的误差参数,将表3中第4列傅里叶系数表达式中的s₃替换为s₃₁和s₃₂的形式,对于矩阵ΔC中以θ为变量的任意一行向量ΔK,ΔK与vec(M)的乘积可以表示为

Δ K vec (Δ M) = - \frac{T_{1} s_{31}}{8} (2 m_{14} + m_{24}) + \frac{T_{3} s_{32}}{8} (2 m_{41} + m_{42}) - \frac{T_{6} (s_{31} + s_{32})}{8} m_{44} + \frac{T_{9} (s_{31} - s_{32})}{8} m_{44} + \frac{T_{10} s_{31}}{8} (2 m_{13} + m_{23}) - \frac{T_{11} s_{31}}{8} (2 m_{12} + m_{22}) + \frac{T_{12} s_{32}}{8} (2 m_{31} + m_{32}) - \frac{T_{13} s_{32}}{8} (2 m_{21} + m_{22}) + T_{14} [\frac{s_{31}}{16} (m_{23} + m_{32}) + \frac{s_{32}}{16} (m_{23} + m_{32})] + T_{15} [- \frac{s_{31}}{16} (m_{22} - m_{33}) - \frac{s_{32}}{16} (m_{22} - m_{33})] + T_{16} [\frac{s_{31}}{16} (m_{23} - m_{32}) - \frac{s_{32}}{16} (m_{23} - m_{32})] + T_{17} [- \frac{s_{31}}{16} (m_{22} + m_{33}) + \frac{s_{32}}{16} (m_{22} + m_{33})] + T_{18} (- \frac{s_{31} m_{24}}{16} - \frac{s_{32} m_{24}}{8}) + T_{19} (- \frac{s_{31} m_{34}}{16} - \frac{s_{32} m_{34}}{8}) + T_{20} (- \frac{s_{31} m_{24}}{16} + \frac{s_{32} m_{24}}{8}) + T_{21} (\frac{s_{31} m_{34}}{16} - \frac{s_{32} m_{34}}{8}) + T_{22} (\frac{s_{31} m_{42}}{8} + \frac{s_{32} m_{42}}{16}) + T_{23} (\frac{s_{31} m_{43}}{8} + \frac{s_{32} m_{43}}{16}) + T_{24} (- \frac{s_{31} m_{42}}{8} + \frac{s_{32} m_{42}}{16}), (21)

式中:T₁~T₂₄为表3中1~24项三角函数基,其自变量为θ,并含参数k。由于ΔC由含不同角度θ的ΔK的表达式组成,因此可将K与vec(M)的乘积视作随机变量。在求这一乘积的方差时,将T₁~T₂₄看作协方差为0,方差均为1/2的随机变量,对各项系数中的穆勒矩阵元素取平方。此时,各穆勒矩阵元素的交叉项可忽略,且在无消偏下所有元素的平方和为4m₁₁₂。

令r₂=sin[σ(Δθ_R)]≈s₃₁/2=s₃₂/2,则

σ [Δ K vec (M)] \approx m_{11} r_{2} 。 (22)

(22)式说明,ΔC与vec(M)的乘积ΔI_eq可以等效成期望为0、标准差为m₁₁r₂的光强噪声。结合(17)式,在波片随机方位角误差θ_R的影响下,穆勒矩阵误差Δ $M_{q ⁃ θ_{R}}$ 的标准差近似为

σ [vec (Δ M_{q ⁃ θ_{R}})] \approx \sqrt[]{diag (S^{T} S)} m_{11} r_{2} 。 (23)

5 仿真验证

5.1 仿真条件

为验证(12)~(15)式表示的简化系统误差模型,以及(17)、(23)式表示的简化随机误差模型的正确性,设定一个原始的被测穆勒光瞳,按表1分别设置各类误差源的参数,并按表4设置各偏振元件的方位角。首先,进行误差正向传递过程的仿真,并根据所得的受误差源影响的一组光强值在理想元件情况下求解测得的穆勒光瞳。

被测穆勒光瞳由一个琼斯光瞳转换而来,该琼斯光瞳提取自一个1.35NA的光刻投影物镜设计的中心视场点^[15],其偏振衰减(D)和相位延迟(R)的分布如图2所示。图中D幅度的均方根(RMS)为0.025,R幅度的RMS为0.05π^[15]。

表 4. 偏振元件角度配置方案

Table 4. Angle configuration of polarization element

Configuration	Angle of P₁θ₁ /(°)	Angle of Q₁ϕ₁ /(°)	Angle of Q₂ϕ₂ /(°)	Angle of P₂θ₂ /(°)
1×144×1	0	0, 1.25, 2.5, …, 178.75	6ϕ₁	0

查看所有表

图 2. 原始琼斯光瞳。(a)偏振衰减;(b)相位延迟

Fig. 2. Original Jones pupil. (a) Polarization attenuation; (b) phase delay

下载图片查看所有图片

基于这种光轴旋转对称的穆勒光瞳,在径向可以对D和R幅度范围内的所有值进行验证,在切向可以对D和R的所有光轴方向进行验证。另外,根据D和R幅度的RMS值,该穆勒光瞳属于小像差光瞳,在所有光瞳点上穆勒矩阵主对角线的元素均接近1,且远大于其他元素。

5.2 系统误差简化模型的仿真验证

将测得的穆勒光瞳与原始光瞳相减,得到穆勒光瞳误差的仿真值,并按(10)~(13)式计算相应光瞳点穆勒矩阵误差的预测值,两者相减得到预测误差。对于任意穆勒矩阵元素的预测误差Δm_ij,在整个光瞳上统计其均值与方差。各类系统误差源的统计结果如图3~5所示,偏振片方位角误差和波片方位角误差的分布规律与之相同,不再画出。

由于在推导波片相位延迟误差的影响时,各项傅里叶系数均可严格匹配,仅使用了一阶近似条件,故简化模型预测误差的平均值和标准差均在10^-6量级。

对于其余三类系统误差,由于各项傅里叶系数无法严格匹配,因此简化模型预测误差的平均值在10^-5量级,标准差在10^-6数量级,而且仍以行数或列数含4的元素的预测误差的标准差较大。从4类不可忽略的系统误差源对应的预测误差的数量级和分布可以看出,所提简化模型的精度较高,能够满足误差分析的需求。

图 3. 波片相位延迟误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 3. Statistics of prediction errors by using model of delay error of retarder. (a) Mean value; (b) standard deviation

下载图片查看所有图片

图 4. 波片偏振衰减误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 4. Statistics of prediction errors by using model of polarization attenuation error of retarder. (a) Mean value; (b) standard deviation

下载图片查看所有图片

图 5. 波片方位角误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 5. Statistics of prediction errors by using model of azimuthal-angle error of retarder. (a) Mean value; (b) standard deviation

下载图片查看所有图片

5.3 随机误差简化模型的仿真验证

对于两种随机误差源,图6给出了两者分别引起的穆勒矩阵误差标准差在整个光瞳上的统计值,这里采用标准差来表示误差分布的不均匀性。可以看出,图像传感器的噪声引起的穆勒矩阵误差与原始穆勒矩阵无关;波片随机方位角误差引起的穆勒矩阵误差在整个光瞳范围内的不均匀性(标准差)在10^-5数量级,说明这一误差与原始穆勒矩阵关系不大。

(22)式将波片随机方位角误差造成的影响近似等效为光强形式的噪声,并给出了噪声方差的表达式。为验证这一表达式对一定范围内的方位角误差Δθ均成立,图7给出了原始和预测的光强误差的标准差随Δθ的变化关系,这里所用的穆勒矩阵为单位矩阵。由于原始光强误差的标准差来自于144次光强仿真统计值,因此这一标准差上下波动。但是,在0~0.5°的范围内,波动的中心位置与(22)式预测的相一致,验证了该式的正确性。

图 6. 两种随机误差引起的穆勒矩阵误差分布的统计值。(a)图像传感器噪声;(b)随机方位角误差

Fig. 6. Statistics of error distribution of Mueller matrix caused by two kinds of random error sources. (a) Image sensor noise; (b) random azimuthal-angle errors of retarders

下载图片查看所有图片

图 7. 原始和预测光强误差与波片随机方位角误差的关系

Fig. 7. Relationship between original and predicted intensity errors and random azimuthal-angle error of retarder

下载图片查看所有图片

将两种随机误差源引起的穆勒矩阵误差(标准差)在整个光瞳范围内取平均,将仿真值与分别按照(17)、(23)式进行计算得到的预测值作对比,分别如图8和图9所示。

图 8. 图像传感器噪声引起的穆勒矩阵误差。(a)原始值;(b)预测值

Fig. 8. Errors of Mueller matrix caused by noise of image sensor. (a) Original values; (b) predicted values

下载图片查看所有图片

图 9. 随机方位角误差引起的穆勒矩阵误差。(a)原始值;(b)预测值

Fig. 9. Errors of Mueller matrix caused by random azimuthal-angle errors of retarders. (a) Original values; (b) predicted values

下载图片查看所有图片

对于图像传感器噪声的影响,由于(17)式基于严格的方差传递公式推导,其预测值与仿真值保持一致;对于波片随机方位角误差的影响,(23)式对非四角元素误差的预测较为准确(误差在10^-4数量级),但对位于矩阵四个角的元素有不可忽略的误差。

6 结论

针对穆勒矩阵成像椭偏仪的系统误差源和随机误差源,分别提出了一种基于傅里叶系数近似匹配的简化分析方法和一种基于等效光强噪声的简化模型。采用所提方法和模型全面分析了椭偏仪的6种系统误差源和2种随机误差源对测得穆勒矩阵的影响,并详细讨论了不同误差源影响的区别与联系。为验证所提简化模型的准确性,对一个典型1.35NA光刻投影物镜的穆勒光瞳进行了含误差源检测仿真。对于4种不可忽略的系统误差源产生的影响,简化模型的预测误差在10^-6~10^-5数量级;对于难以从解析角度分析的波片随机方位角误差产生的影响,简化模型的预测误差在10^-4数量级。所提的两类简化模型,其精度均可满足误差分析和预测的需求,且与同类方法相比具有简单清晰的表达式,适用于穆勒矩阵成像椭偏仪的综合误差评定、误差源指标分解,以及元件误差标定和补偿。

参考文献

[1] Fujii T, Kogo J, Suzuki K, et al. Polarization characteristics of state-of-art lithography optics reconstructed from on-body measurement[J]. Proceedings of SPIE, 2008, 6924: 69240Z.

[2] McGuire J P, Chipman R A. Polarization aberrations in optical systems[J]. Proceedings of SPIE, 1987, 818: 240-257.

[3] McGuire J P, Chipman R A. Polarization aberrations. 1. Rotationally symmetric optical systems[J]. Applied Optics, 1994, 33(22): 5080-5100.

[4] Kye J. Polarization aberrations in hyper-numerical-aperture projection printing: a comparison of various representations[J]. Nanolithography, MEMS, and MOEMS, 2006, 5(3): 033001.

[5] Kye J. McIntyre G, Norihiro Y, et al. Polarization aberration analysis in optical lithography systems[J]. Proceedings of SPIE, 2006, 6154: 61540E.

[6] Totzeck M, Graupner P, Heil T, et al. How to describe polarization influence on imaging[J]. Proceedings of SPIE, 2004, 5754: 23-37.

[7] Pezzaniti J L, Chipman R A. Mueller matrix imaging polarimetry[J]. Optical Engineering, 1995, 34(6): 1558-1568.

[8] Goldstein D H, Chipman R A. Error analysis of a Mueller matrix polarimeter[J]. Journal of the Optical Society of America A, 1990, 7(4): 693-700.

[9] Bhattacharyya K. Serrano-García D I, Otani Y. Accuracy enhancement of dual rotating mueller matrix imaging polarimeter by diattenuation and retardance error calibration approach[J]. Optics Communications, 2017, 392: 48-53.

[10] Nee S M F. Error analysis for Mueller matrix measurement[J]. Journal of the Optical Society of America A, 2003, 20(8): 1651-1657.

[11] Savenkov S N, Klimov A S, Oberemok E A. Error in determining Mueller matrix elements and its effect on solution of the inverse problem of polarimetry[J]. Journal of Applied Spectroscopy, 2009, 76(5): 743-751.

[12] Broch L, En Naciri A, Johann L. Systematic errors for a Mueller matrix dual rotating compensator ellipsometer[J]. Optics Express, 2008, 16(12): 8814-8824.

[13] Broch L, En Naciri A, Johann L. Second-order systematic errors in Mueller matrix dual rotating compensator ellipsometry[J]. Applied Optics, 2010, 49(17): 3250-3258.

[14] Anna G, Goudail F. Optimal Mueller matrix estimation in the presence of Poisson shot noise[J]. Optics Express, 2012, 20(19): 21331-21340.

[15] Meng Z J, Li S K, Wang X Z, et al. Jones pupil metrology of lithographic projection lens and its optimal configuration in the presence of error sources[J]. Optics Express, 2019, 27(4): 4629-4647.

3.2 波片的偏振衰减误差和方位角误差分析

孟泽江, 李思坤, 王向朝, 步扬, 戴凤钊, 杨朝兴. 穆勒矩阵成像椭偏仪误差源的简化分析方法[J]. 光学学报, 2019, 39(9): 0911002. Zejiang Meng, Sikun Li, Xiangzhao Wang, Yang Bu, Fengzhao Dai, Chaoxing Yang. Simplified Analytical Method for Error Sources in Mueller Matrix Imaging Polarimeter[J]. Acta Optica Sinica, 2019, 39(9): 0911002.

穆勒矩阵成像椭偏仪误差源的简化分析方法 下载： 965次

1 引言

2 基本原理

2.1 穆勒矩阵成像椭偏仪的测量原理

图 1. 用于偏振像差检测的穆勒矩阵成像椭偏仪的结构图

Fig. 1. Structure of Mueller matrix imaging polarimeter for measuring polarization aberration

2.2 穆勒矩阵成像椭偏仪的误差源

表 1. 穆勒矩阵成像椭偏仪的误差源

Table 1. Error sources in Mueller matrix imaging polarimeter

3 系统误差源的简化分析方法

3.1 波片的相位延迟误差分析

表 2. 含波片相位延迟误差的光强傅里叶系数

Table 2. Fourier coefficients of light intensity influenced by delay errorof retarder

3.2 波片的偏振衰减误差和方位角误差分析

表 3. 含波片偏振衰减和方位角误差的光强傅里叶系数

Table 3. Fourier coefficients of light intensity influenced by diattenuation and azimuthal-angle error of retarder

3.3 偏振片的三种系统误差分析

4 随机误差源的简化模型

4.1 图像传感器噪声分析

4.2 波片的随机角度误差分析

5 仿真验证

5.1 仿真条件

表 4. 偏振元件角度配置方案

Table 4. Angle configuration of polarization element

图 2. 原始琼斯光瞳。(a)偏振衰减;(b)相位延迟

Fig. 2. Original Jones pupil. (a) Polarization attenuation; (b) phase delay

5.2 系统误差简化模型的仿真验证

图 3. 波片相位延迟误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 3. Statistics of prediction errors by using model of delay error of retarder. (a) Mean value; (b) standard deviation

图 4. 波片偏振衰减误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 4. Statistics of prediction errors by using model of polarization attenuation error of retarder. (a) Mean value; (b) standard deviation

图 5. 波片方位角误差模型的预测误差统计值。(a)平均值;(b)标准差

Fig. 5. Statistics of prediction errors by using model of azimuthal-angle error of retarder. (a) Mean value; (b) standard deviation

5.3 随机误差简化模型的仿真验证

图 6. 两种随机误差引起的穆勒矩阵误差分布的统计值。(a)图像传感器噪声;(b)随机方位角误差

Fig. 6. Statistics of error distribution of Mueller matrix caused by two kinds of random error sources. (a) Image sensor noise; (b) random azimuthal-angle errors of retarders

图 7. 原始和预测光强误差与波片随机方位角误差的关系

Fig. 7. Relationship between original and predicted intensity errors and random azimuthal-angle error of retarder

图 8. 图像传感器噪声引起的穆勒矩阵误差。(a)原始值;(b)预测值

Fig. 8. Errors of Mueller matrix caused by noise of image sensor. (a) Original values; (b) predicted values

图 9. 随机方位角误差引起的穆勒矩阵误差。(a)原始值;(b)预测值

Fig. 9. Errors of Mueller matrix caused by random azimuthal-angle errors of retarders. (a) Original values; (b) predicted values

6 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

穆勒矩阵成像椭偏仪误差源的简化分析方法下载： 965次