Experimental test of error-disturbance uncertainty relation with continuous variables

Yang Liu; Haijun Kang; Dongmei Han; Xiaolong Su; Kunchi Peng

doi:doi:10.1364/PRJ.7.000A56

Photonics Research, 2019, 7 (11): 11000A56, Published Online: Oct. 30, 2019

Experimental test of error-disturbance uncertainty relation with continuous variables Download： 590次

论文大纲

Yang Liu ¹Haijun Kang ¹Dongmei Han ¹Xiaolong Su ^1,2,*Kunchi Peng ^1,2

Author Affiliations

¹ State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

² Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Abstract

The uncertainty relation is one of the fundamental principles in quantum mechanics and plays an important role in quantum information science. We experimentally test the error-disturbance uncertainty relation (EDR) with continuous variables for Gaussian states. Two incompatible continuous-variable observables, amplitude and phase quadratures of an optical mode, are measured simultaneously using a heterodyne measurement system. The EDR values with continuous variables for coherent, squeezed, and thermal states are verified experimentally. Our experimental results demonstrate that Heisenberg’s EDR with continuous variables is violated, while Ozawa’s and Branciard’s EDRs with continuous variables are validated.

1. INTRODUCTION

As one of the cornerstones of quantum mechanics, the uncertainty relation describes the measurement limitation on two incompatible observables. The uncertainty relation has a huge impact on areas of quantum information technology such as entanglement verification ^[1], quantum key distribution ^[2], quantum dense coding ^{[35" target="_self" style="display: inline;">–5]}, and security of quantum cryptography ^[6]. Heisenberg’s original uncertainty relation is related to measurement effect, which states that we cannot acquire perfect knowledge of a state without disturbing it ^[7].

There are two kinds of uncertainty relations, the preparation and the measurement uncertainty relations, depending on whether one is talking about average measurement or one-shot measurement in the understanding of Heisenberg’s spirit. The preparation uncertainty relation studies the minimal dispersion of two quantum observables before measurement ^{[810" target="_self" style="display: inline;">–10]}. The Robertson uncertainty relation, which reads as $σ (x) σ (p) \geq ℏ / 2$ , is a typical example in this sense, where $σ (x)$ and $σ (p)$ are the standard deviations of position and momentum ^[10]. For such uncertainty relations, the measurements of $x$ and $p$ are performed on an ensemble of identically prepared quantum systems. The measurement uncertainty relation holds that Heisenberg’s uncertainty principle should be based on the observer’s effect, which means that measurements of certain systems cannot be made without affecting the system. This kind of uncertainty relation, which studies the extent to which the accuracy of a position measurement is related to the disturbance of the particle’s momentum, is also called the error-disturbance relation (EDR) ^{[1113" target="_self" style="display: inline;">–13]}.

Heisenberg’s EDR is generally expressed as where $C_{A B} = | ⟨ [A, B] ⟩ | / 2$ , $[A, B] = A B - B A$ , $ε (A) = {⟨ {(C - A)}^{2} ⟩}^{1 / 2}$ , and $η (B) = {⟨ {(D - B)}^{2} ⟩}^{1 / 2}$ represent the root-mean-square (RMS) difference between the initial values of $A$ and $B$ and the outcome values of a measurement of $C$ and $D$ , respectively. However, it has been shown that Heisenberg’s EDR is not valid in some cases ^[11]. Heated debates on EDR have since taken place, and new formulated EDRs have been put forward ^{[12–24" target="_self" style="display: inline;">–24]}. Ozawa proposed the EDR as Branciard then improved Ozawa’s EDR as ^[16] which is tighter than Ozawa’s EDR. The experimental tests of the uncertainty relations have been demonstrated in spin-1/2 ^{[25–28" target="_self" style="display: inline;">–28]}, photonic ^{[29–34" target="_self" style="display: inline;">–34]}, nuclear spin ^[35], and ion-trap ^[36,37] systems. All of these experimental tests of EDR are limited in discrete-variable systems.

In the original thought experiment proposed by Heisenberg, two continuous variables, position and momentum of a particle, are used to describe the measurement uncertainty relation. Thus, the experimental test of EDR based on a continuous-variable system reflects Heisenberg’s original idea more precisely, and will make the test of the uncertainty relation more complete. Very recently, an experimental test of the error-tradeoff uncertainty relation with continuous variables was demonstrated using an Einstein–Podolsky–Rosen (EPR) entangled state ^[38].

In this paper, we report an experimental test of EDR with continuous variables using a heterodyne measurement system. An advantage of our experiment is that we can test the EDR with continuous variables for different signal states by changing the input state of the heterodyne measurement system. In our experiment, we test the EDR for three different Gaussian states: coherent, squeezed, and thermal states. A vacuum mode is used as meter mode in the measurement system. Our experimental results demonstrate that Heisenberg’s EDR with continuous variables is violated, while Ozawa’s and Branciard’s EDRs with continuous variables are validated.

2. PRINCIPLE AND EXPERIMENTAL SETUP

The amplitude and phase quadratures of an optical mode are incompatible continuous-variable observables, and cannot be measured simultaneously. A heterodyne measurement system, which is a joint measurement apparatus, can be used to measure the approximations of $A$ and $B$ with the compatible observables $C$ and $D$ , as shown in Fig. 1(a). The signal mode $ρ$ with incompatible observables $A = {\hat{x}}_{ρ}$ and $B = {\hat{p}}_{ρ}$ is coupled with a meter mode via a beam-splitter (BS), where $\hat{x} = \hat{a} + {\hat{a}}^{†}$ and $\hat{p} = (\hat{a} - {\hat{a}}^{†}) / i$ denote the amplitude and phase quadratures of an optical mode, respectively. In this case, the righthand sides of EDRs in Eqs. (1)–(3) are given by $C_{A B} = 1$ .

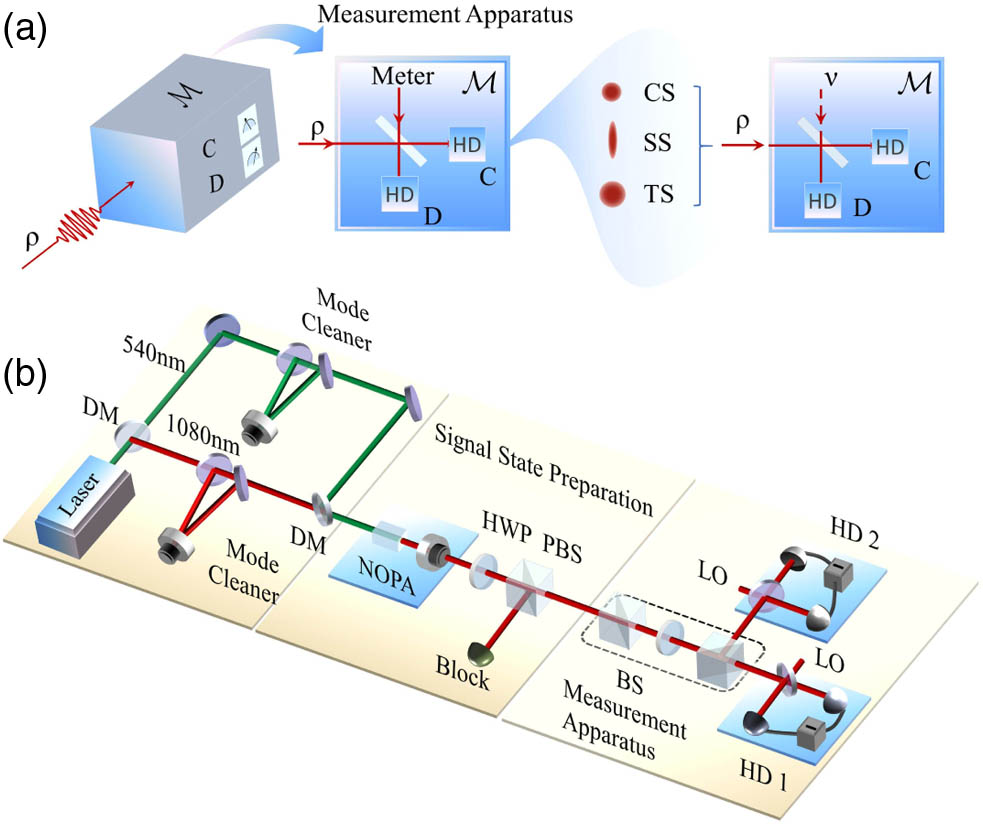
(a) Principle of the test of EDR with continuous variables. A joint measurement apparatus implements the approximations of incompatible observables A and B with the compatible observables C and D by coupling the signal and meter modes via a beam-splitter. Coherent state (CS), squeezed state (SS), and thermal state (TS) serve as signal modes, and a vacuum state serves as meter mode. (b) Schematic of the experimental setup. Signal state is prepared by a NOPA. The measurement apparatus is composed by a BS, which is a combination of PBS–HWP–PBS, and two HDs. Two output modes of the BS are detected by HD1 and HD2, respectively. NOPA, nondegenerate optical parametric amplifier; BS, beam-splitter; HWP, half-waveplate; PBS, polarization beam-splitter; HD, homodyne detector; LO, local oscillator.

Fig. 1. (a) Principle of the test of EDR with continuous variables. A joint measurement apparatus implements the approximations of incompatible observables $A$ and $B$ with the compatible observables $C$ and $D$ by coupling the signal and meter modes via a beam-splitter. Coherent state (CS), squeezed state (SS), and thermal state (TS) serve as signal modes, and a vacuum state serves as meter mode. (b) Schematic of the experimental setup. Signal state is prepared by a NOPA. The measurement apparatus is composed by a BS, which is a combination of PBS–HWP–PBS, and two HDs. Two output modes of the BS are detected by HD1 and HD2, respectively. NOPA, nondegenerate optical parametric amplifier; BS, beam-splitter; HWP, half-waveplate; PBS, polarization beam-splitter; HD, homodyne detector; LO, local oscillator.

下载图片查看所有图片

The signal mode is prepared as coherent, squeezed, and thermal states, and a vacuum state $ν$ is used as the meter mode in our experiment. The amplitude quadrature $C = {\hat{x}}_{c} = \sqrt{T} {\hat{x}}_{ρ} - \sqrt{R} {\hat{x}}_{ν}$ and phase quadrature $D = {\hat{p}}_{d} = \sqrt{R} {\hat{p}}_{ρ} + \sqrt{T} {\hat{p}}_{ν}$ of two output modes of BS $c$ and $d$ are measured by two homodyne detectors simultaneously, which are used to approximate $A$ and $B$ , respectively, where $T$ is the transmission efficiency of the BS, and $R = 1 - T$ ^[39]. The RMS error and disturbance are expressed as respectively.

The experimental setup for test of EDR is illustrated in Fig. 1(b). A laser generates both 1080 and 540 nm optical fields simultaneously. The 1080 nm optical field is used as the injected signal of a nondegenerate optical parametric amplifier (NOPA) and the local oscillator fields of homodyne detectors. The 540 nm optical field serves as the pump field of the NOPA. A half-waveplate (HWP) and a polarization beam-splitter (PBS), which are placed after the NOPA, are used to obtain different signal modes. The measurement apparatus is composed by a BS and two homodyne detectors. The AC output signals from HD1 and HD2 are mixed with a local reference signal of 3 MHz, and then filtered by low-pass filters with a bandwidth of 30 kHz and amplified 1000 times (low-noise preamplifier, SRS, SR560). Then, the two signals from the outputs of the preamplifiers are recorded by a digital storage oscilloscope simultaneously. A sample size of $5 \times 10^{5}$ data points is used for all quadrature measurements. The interference efficiencies between signal and local oscillator fields of the HDs are 99%, and the quantum efficiencies of the photodiodes are 99.6%.

3. RESULTS

A coherent state is prepared when the pump field of the NOPA is blocked and only the injected field passes through the NOPA. The variances of amplitude and phase quadratures of the coherent and vacuum states (meter mode) are $σ {({\hat{x}}_{ρ})}^{2} = σ {({\hat{p}}_{ρ})}^{2} = 1$ and $σ {({\hat{x}}_{ν})}^{2} = σ {({\hat{p}}_{ν})}^{2} = 1$ , respectively ^[39]. When the NOPA is operated at the parametric deamplification situation and the half-waveplate after the NOPA is set to 22.5°, $x$ -squeezed and $p$ -squeezed states are prepared. The $x$ -squeezed state is used as the signal mode in the test of EDR for the squeezed state. The variances of the amplitude and phase quadratures of the $x$ -squeezed state are $σ {({\hat{x}}_{ρ})}^{2} = e^{- 2 r}$ and $σ {({\hat{p}}_{ρ})}^{2} = e^{2 r}$ , respectively, where $r$ is the squeezing parameter ^[39,40]. In the experiment, the squeezed state with $- 2.9 dB$ squeezing and 3.9 dB antisqueezing is generated by the NOPA. When the half-waveplate after the NOPA is set to 0°, the EPR entangled state is generated. Each mode of the entangled state is a thermal state, and one of them is used for the EDR test for the thermal state. The variances of the amplitude and phase quadratures of the thermal state are $σ {({\hat{x}}_{ρ})}^{2} = σ {({\hat{p}}_{ρ})}^{2} = (e^{- 2 r} + e^{2 r}) / 2$ ^[39].

The amplitude quadrature $\hat{x}$ and phase quadrature $\hat{p}$ are measured by locking the relative phase difference between the signal mode and local oscillator to 0 and $π / 2$ in the homodyne detector, respectively. When ${\hat{x}}_{c}$ and ${\hat{x}}_{d}$ ( ${\hat{p}}_{c}$ and ${\hat{p}}_{d}$ ) are recorded in the time domain simultaneously, the error $ε (A)$ and disturbance $η (B)$ are obtained according to Eqs. (4) and (5), respectively. The Heisenberg’s EDR is verified by the obtained error $ε (A)$ and disturbance $η (B)$ according to Eq. (1). Then we measure the signal mode $ρ$ by HD1 directly by removing the BS to obtain the variances of amplitude and phase quadratures $σ {({\hat{x}}_{ρ})}^{2}$ and $σ {({\hat{p}}_{ρ})}^{2}$ , respectively. After we have measurement results for $ε (A), η (B), σ ({\hat{x}}_{ρ})$ , and $σ ({\hat{p}}_{ρ})$ , the lefthand sides of the Ozawa and Branciard EDRs can be obtained according to Eqs. (2) and (3), respectively.

The dependence of error of the amplitude quadrature $ε (A)$ and disturbance of the phase quadrature $η (B)$ on the transmission efficiency of BS for three different Gaussian signal modes is shown in Figs. 2(a)–2(c), respectively. The error $ε (A)$ decreases with the increasing of the transmission efficiency of the BS, while the disturbance $η (B)$ increases with the increasing of the transmission efficiency for all of the three Gaussian states. When the error reaches the minimum value, the maximum disturbance is caused. The reduction of disturbance in one observable can be realized at the expense of increasing error in the other observable. When an $x$ -squeezed state serves as signal mode, the maximum error is less than the case in which the coherent state serves as signal field with the cost of the greater maximum disturbance for the anti-squeezing of the phase quadrature [Fig. 2(b)]. When the signal mode is a thermal state, both the error and disturbance of the state are larger than that of the coherent state at the same transmission efficiency of BS, as shown in Figs. 2(a) and 2(c).

Experimental results. (a), (b) and (c) Dependence of error (black curve) and disturbance (red curve) on the transmission efficiency of BS (T) for coherent, squeezed, and thermal states, respectively. (d), (e) and (f) Lefthand sides of the EDRs with continuous variables for coherent, squeezed, and thermal states, respectively. Green curve, Heisenberg’s EDR; red curve, Ozawa’s EDR; blue curve, Branciard’s EDR. Black line, righthand side of the EDR. All experimental data agree well with the theoretical predictions. The error bars are obtained by RMS of measurements repeated ten times.

Fig. 2. Experimental results. (a), (b) and (c) Dependence of error (black curve) and disturbance (red curve) on the transmission efficiency of BS (T) for coherent, squeezed, and thermal states, respectively. (d), (e) and (f) Lefthand sides of the EDRs with continuous variables for coherent, squeezed, and thermal states, respectively. Green curve, Heisenberg’s EDR; red curve, Ozawa’s EDR; blue curve, Branciard’s EDR. Black line, righthand side of the EDR. All experimental data agree well with the theoretical predictions. The error bars are obtained by RMS of measurements repeated ten times.

下载图片查看所有图片

The dependence of the lefthand side of Ozawa’s (red curve), Branciard’s (blue curve), and Heisenberg’s (green curve) EDRs on the transmission efficiency of BS for three Gaussian states is shown in Figs. 2(d)–2(f), respectively. It is clear that the Ozawa’s and Branciard’s EDRs with continuous variables are valid, while Heisenberg’s EDR with continuous variable is violated. Comparing the blue and red curves, we can see that the Branciard’s EDR is tighter than Ozawa’s EDR with continuous variables. When the transmission efficiency is 50%, the lefthand side of Branciard’s EDR with continuous variables reaches its minimum value in the case of coherent and thermal states. In the case of the $x$ -squeezed state serving as signal mode, the Branciard’s inequality is minimized when the transmission efficiency is about 95%, which is because the variances of amplitude and phase quadratures of the squeezed state are unequal.

The comparison of the lower bounds of EDRs for three Gaussian states in the error-disturbance plot is shown in Fig. 3. The results for coherent, squeezed, and thermal states are shown in Figs. 3(a)–3(c), respectively. All the experimental results demonstrate that Heisenberg’s EDR with continuous variables is violated, yet Ozawa’s and Branciard’s EDRs with continuous variables are valid.

Comparison of the lower bounds of EDRs for three Gaussian states. (a) Coherent state as signal mode. (b) Squeezed state as signal mode. (c) Thermal state as signal mode. Blue curve, Heisenberg bound; orange curve, Ozawa bound; green curve, Branciard bound. Black circles show experimental data. Black dotted curve shows the theoretical prediction for the experimental parameters.

Fig. 3. Comparison of the lower bounds of EDRs for three Gaussian states. (a) Coherent state as signal mode. (b) Squeezed state as signal mode. (c) Thermal state as signal mode. Blue curve, Heisenberg bound; orange curve, Ozawa bound; green curve, Branciard bound. Black circles show experimental data. Black dotted curve shows the theoretical prediction for the experimental parameters.

下载图片查看所有图片

4. DISCUSSION AND CONCLUSION

Comparing the experimental tests of EDR with discrete and continuous variables, the main difference is that the quantum states (quantum observables) used in the experiments are different. In the presented paper, amplitude and phase quadratures of Gaussian states are applied. The main results of the experimental tests of EDR with discrete and continuous variables are the same, which confirms that the Heisenberg’s EDR can be violated in some cases, while the improved Ozawa and Branciard EDRs are valid ^{[25–33" target="_self" style="display: inline;">–33]}. There are also some experimental tests of EDR proposed by Busch, Lahti, and Werner with discrete variables ^{[3537" target="_self" style="display: inline;">–37]}, but the experimental test of this EDR with continuous variables has not been reported.

Comparing this experiment with the test of error-tradeoff uncertainty relation reported in Ref. ^[38], there are two differences. First, the quantum states used to demonstrate the error-disturbance relation with continuous variables are different. In Ref. ^[38], an EPR entangled state is used in the experiment, while in this paper, three different Gaussian states are used in the experiment: coherent, squeezed, and thermal states. The results for non-zero error and disturbance of these three Gaussian states are presented. Second, the measurement schemes used in these two experiments are different. In Ref. ^[38], the amplitude and phase quadratures of two EPR beams are measured by two homodyne detectors simultaneously. One of the EPR beams plays the role of the meter field. In this paper, the heterodyne measurement system is used to measure the amplitude and phase quadratures of an optical mode simultaneously. The vacuum is used as the meter field. This scheme is a general test of EDR with continuous variables for an optical mode.

In summary, we experimentally test the Heisenberg, Ozawa, and Branciard EDRs with continuous variables using a heterodyne measurement system. Three different Gaussian states, i.e., coherent, squeezed, and thermal states, are used as signal mode to test the EDRs. All the experimental results demonstrate that Heisenberg’s EDR is violated, yet Ozawa’s and Branciard’s EDRs are validated. Our work represents an important advance in understanding the fundamentals of physical measurement, and sheds light on the development of quantum information technology.

References

[1] F. Buscemi. All entangled quantum states are nonlocal. Phys. Rev. Lett., 2012, 108: 200401.

[2] F. Furrer, T. Franz, M. Berta, A. Leverrier, V. B. Scholz, M. Tomamichel, R. F. Werner. Continuous variable quantum key distribution: finite-key analysis of composable security against coherent attacks. Phys. Rev. Lett., 2012, 109: 100502.

[3] C. H. Bennett, S. J. Wiesner. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett., 1992, 69: 2881-2884.

[4] X. Li, Q. Pan, J. Jing, J. Zhang, C. Xie, K. Peng. Quantum dense coding exploiting a bright Einstein-Podolsky-Rosen beam. Phys. Rev. Lett., 2002, 88: 047904.

[5] J. Jin, J. Zhang, Y. Yan, F. Zhao, C. Xie, K. Peng. Experimental demonstration of tripartite entanglement and controlled dense coding for continuous variables. Phys. Rev. Lett., 2003, 90: 167903.

[6] N. Gisin, G. Ribordy, W. Tittel, H. Zbinden. Quantum cryptography. Rev. Mod. Phys., 2002, 74: 145-195.

[7] W. Heisenberg. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys., 1927, 43: 172-198.

[8] E. H. Kennard. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys., 1927, 44: 326-352.

[9] WeylH., Gruppentheorie und Quantenmechanik (University of California, 1928).

[10] H. P. Robertson. The uncertainty principle. Phys. Rev., 1929, 34: 163-164.

[11] L. E. Ballentine. The statistical interpretation of quantum mechanics. Rev. Mod. Phys., 1970, 42: 358-381.

[12] M. Ozawa. Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurements. Phys. Rev. A, 2003, 67: 042105.

[13] M. J. W. Hall. Prior information: how to circumvent the standard joint-measurement uncertainty relation. Phys. Rev. A, 2004, 69: 052113.

[14] M. Ozawa. Uncertainty relations for joint measurements of noncommuting observables. Phys. Lett. A, 2004, 320: 367-374.

[15] M. Ozawa. Soundness and completeness of quantum root-mean-square errors. NPJ Quantum Inf., 2019, 5: 1.

[16] C. Branciard. Error-tradeoff and error-disturbance relations for incompatible quantum measurements. Proc. Natl. Acad. Sci. USA, 2013, 110: 6742-6747.

[17] P. Busch, P. Lahti, R. F. Werner. Heisenberg uncertainty for qubit measurements. Phys. Rev. A, 2014, 89: 012129.

[18] P. Busch, P. Lahti, R. F. Werner. Colloquium: quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys., 2014, 86: 1261-1281.

[19] J. Dressel, F. Nori. Certainty in Heisenberg’s uncertainty principle: revisiting definitions for estimation errors and disturbance. Phys. Rev. A, 2014, 89: 022106.

[20] K. Baek, T. Farrow, W. Son. Optimized entropic uncertainty relation for successive measurement. Phys. Rev. A, 2014, 89: 032108.

[21] F. Buscemi, M. J. W. Hall, M. Ozawa, M. M. Wilde. Noise and disturbance in quantum measurements: an information-theoretic approach. Phys. Rev. Lett., 2014, 112: 050401.

[22] X. M. Lu, S. Yu, K. Fujikawa, C. H. Oh. Improved error-tradeoff and error-disturbance relations in terms of measurement error components. Phys. Rev. A, 2014, 90: 042113.

[23] A. Barchielli, M. Gregoratti, A. Toigo. Measurement uncertainty relations for position and momentum: relative entropy formulation. Entropy, 2017, 19: 301.

[24] A. Barchielli, M. Gregoratti, A. Toigo. Measurement uncertainty relations for discrete observables: relative entropy formulation. Commun. Math. Phys., 2018, 357: 1253-1304.

[25] J. Erhart, S. Sponar, G. Sulyok, G. Badurek, M. Ozawa, Y. Hasegawa. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements. Nat. Phys., 2012, 8: 185-189.

[26] G. Sulyok, S. Sponar, J. Erhart, G. Badurek, M. Ozawa, Y. Hasegawa. Violation of Heisenberg’s error-disturbance uncertainty relation in neutron-spin measurements. Phys. Rev. A, 2013, 88: 022110.

[27] G. Sulyok, S. Sponar, B. Demirel, F. Buscemi, M. J. W. Hall, M. Ozawa, Y. Hasegawa. Experimental test of entropic noise-disturbance uncertainty relations for spin-1/2 measurements. Phys. Rev. Lett., 2015, 115: 030401.

[28] B. Demirel, S. Sponar, G. Sulyok, M. Ozawa, Y. Hasegawa. Experimental test of residual error-disturbance uncertainty relations for mixed spin-1/2 states. Phys. Rev. Lett., 2016, 117: 140402.

[29] M. Ringbauer, D. N. Biggerstaff, M. A. Broome, A. Fedrizzi, C. Branciard, A. G. White. Experimental joint quantum measurements with minimum uncertainty. Phys. Rev. Lett., 2014, 112: 020401.

[30] F. Kaneda, S. Y. Baek, M. Ozawa, K. Edamatsu. Experimental test of error-disturbance uncertainty relations by weak measurement. Phys. Rev. Lett., 2014, 112: 020402.

[31] L. A. Rozema, A. Darabi, D. H. Mahler, A. Hayat, Y. Soudagar, A. M. Steinberg. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett., 2012, 109: 100404.

[32] A. P. Lund, H. M. Wiseman. Measuring measurement-disturbance relationships with weak values. New J. Phys., 2010, 12: 093011.

[33] S. Y. Baek, F. Kaneda, M. Ozawa, K. Edamatsu. Experimental violation and reformulation of the Heisenberg’s error-disturbance uncertainty relation. Sci. Rep., 2013, 3: 2221.

[34] M. M. Weston, M. J. W. Hall, M. S. Palsson, H. M. Wiseman, G. J. Pryde. Experimental test of universal complementarity relations. Phys. Rev. Lett., 2013, 110: 220402.

[35] W. Ma, Z. Ma, H. Wang, Z. Chen, Y. Liu, F. Kong, Z. Li, X. Peng, M. Shi, F. Shi, S. Fei, J. Du. Experimental test of Heisenberg’s measurement uncertainty relation based on statistical distances. Phys. Rev. Lett., 2016, 116: 160405.

[36] F. Zhou, L. Yan, S. Gong, Z. Ma, J. He, T. Xiong, L. Chen, W. Yang, M. Feng, V. Vedral. Verifying Heisenberg’s error-disturbance relation using a single trapped ion. Sci. Adv., 2016, 2: e1600578.

[37] T. Xiong, L. Yan, Z. Ma, F. Zhou, L. Chen, W. Yang, M. Feng, P. Busch. Optimal joint measurements of complementary observables by a single trapped ion. New J. Phys., 2017, 19: 063032.

[38] Y. Liu, Z. Ma, H. Kang, D. Han, M. Wang, Z. Qin, X. Su, K. Peng. Experimental test of error-tradeoff uncertainty relation using a continuous-variable entangled state. NPJ Quantum Inf., 2019, 5: 68.

[39] C. Weedbrook, S. Pirandola, R. García-Patrón, N. J. Cerf, T. C. Ralph, J. H. Shapiro, S. Lloyd. Gaussian quantum information. Rev. Mod. Phys., 2012, 84: 621-669.

[40] X. Su, S. Hao, X. Deng, L. Ma, M. Wang, X. Jia, C. Xie, K. Peng. Gate sequence for continuous variable one-way quantum computation. Nat. Commun., 2013, 4: 2828.

1. INTRODUCTION

2. PRINCIPLE AND EXPERIMENTAL SETUP

3. RESULTS

4. DISCUSSION AND CONCLUSION

Yang Liu, Haijun Kang, Dongmei Han, Xiaolong Su, Kunchi Peng. Experimental test of error-disturbance uncertainty relation with continuous variables[J]. Photonics Research, 2019, 7(11): 11000A56.

Experimental test of error-disturbance uncertainty relation with continuous variables Download： 590次

1. INTRODUCTION

2. PRINCIPLE AND EXPERIMENTAL SETUP

3. RESULTS

4. DISCUSSION AND CONCLUSION

Article Outline

关于本站 Cookie 的使用提示

全站搜索

Experimental test of error-disturbance uncertainty relation with continuous variables Download： 590次

1. INTRODUCTION

2. PRINCIPLE AND EXPERIMENTAL SETUP

3. RESULTS

4. DISCUSSION AND CONCLUSION

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索