1 Introduction

Structured light¹ refers to the modern-day ability to tailor light in all its degrees of freedom (DoFs), spatial and temporal, to create complex optical fields in both the classical^2-5 and quantum^{6, 7} domains. Combining DoFs have given rise to novel and exotic states of light as 2D, 3D and even 4D fields, including optical knots^{8, 9}, skyrmions^{10, 11}, Mobius strips¹², spatio-temporal fields^13-16, ray-wave structured fields^{17, 18}, quantum-like classical light^19-21 and photonic wheels²². But although the progress has been rapid of late, the topic itself can be dated back to Thomas Young and his double slit experiment, where arguably the first structured light was created. Indeed, the very essence of structured light is the notion of superpositions, where interference (not necessarily in intensity) gives rise to the desired structure. Today one can formulate all of structured light as a linear superposition principle¹, giving rise to geometric representations of the superpositions, from the orbital angular momentum (OAM)²³, to the total angular momentum²⁴ of light, and more recently a generalised framework for multiple DoFs²⁵. For example, even simple plane waves hold the potential for structure: one plane wave may have a phase gradient, two plane waves will give rise to an intensity structure (as done by Young more than 200 years ago), three plane waves can produce an optical phase singularity, while multiple plane waves can give rise to exotic families of structured light, for instance, planes waves travelling on a cone give rise to Bessel beams²⁶. If the interfering plane waves are allowed to hold information in another DoF, say polarization, then just two can create exotic polarization structures²⁷ and if focussed, will create synthetic chiral light in 3D²⁸. It is clear that there is a strong link between interference, a linear effect, and structured light. For this reason, the vast bulk of studies involving structured light have considered linear optical elements, with only much more recent progress in nonlinear optics with structured light, the topic of this review.

The invention of the laser²⁹ is seen as fundamental to the development of the research field of nonlinear optics, with the first nonlinear optical demonstration of second harmonic generation (SHG)³⁰ following quickly, soon after by third harmonic generation³¹ and SHG carrying spin angular momentum (SAM)³². The reason for the strong historical linkage is simple: nonlinear optical phenomena are weak and typically need a coherent high power source to be observed. This knowledge can be dated back as far a Fresnel, who already understood that wave superpositions could transcend the linear regime. With the development of stronger laser sources and more efficient nonlinear materials, we have overcome this requirement. It is only natural then that the study of nonlinear optical phenomena shifts from asking “how much light is there?” based on efficiency concerns (intensity being the key to address this), to “what does the light look like?” (the structure of the light). Seminal works began analysing the structure of the generated light three decades ago³³ with early work demonstrating the doubling of the number of singularities in the generated field³⁴. Following the link between orbital angular momentum (OAM) and these so-called screw dislocations (see ref.³⁵ and references therein), the use of OAM carrying Laguerre-Gaussian (LG) modes in nonlinear optics was demonstrated³⁶ followed a little later by the first production of quantum structured photons by nonlinear optics, demonstrating OAM entangled states³⁷. Although these important works set the scene, further progress has been slow, until only recently.

In this review we follow the progress in the field, from intensity drive processes that serve to alter the frequency of the pump light, to the present day nonlinear toolkit for the creation, manipulation and detection of structured light. We begin with the familiar wave mixing processes of second order, which have been deeply explored and continue to develop to this day, serving to exemplify how counter-intuitive these interactions can be with the introduction of structured light. We then move on to show the types of media that allow these process and how they can also be structured, playing a crucial role in recent advances. We expand into higher-order parametric processes, including third harmonic generation and the generation of optical vortex solitons. Finally, we cite recent developments in high harmonic generation, an extreme non-parametric process, and the unusual applications of nonlinear processes in the quantum regime.

2 Theoretical background

The field of nonlinear optics is a venerable topic, and the reader is referred to excellent textbooks on the topic^38-40. For the benefit of the reader, We begin by briefly outlining the core theory needed for the review, and to this end we begin with Maxwell's equations in the presence of a medium. If condensed and rewritten in terms of a wave equation, one finds,

1[∇×∇×+1c2∂2∂t2]E=−4πc2∂2P∂t2,

where E is the electric field and P is the polarization of the medium. This describes the response of the medium to the input electric field, and the counter response of the polarised medium on the field. In a analogy to the harmonic oscillator, we can do a perturbative expansion of the medium polarization in a power series of the electric field strength,

2Pi=χij(1)Ej+χijk(2)EjEk+χijkl(3)EjEkEl+⋯,

where Pi is the i component of P and χ(n) is the n−th order susceptibility tensor, a tensor of the n−th order. The first term is responsible for the well known linear optical effects, such as refraction and birefringence. All other terms are referred to as nonlinear parametric effects, which this review will mostly feature. This expansion describes a plethora of nonlinear optical effects, such as wave-mixing, self and cross phase modulation, among many. For example, the second order term, with its second order susceptibility tensor, allows the medium polarisability to be separated in frequency components. Second order wave mixing can result in effects such as second harmonic generation, sum frequency generation, difference frequency generation and optical rectification, with a well understood rule set.

But what are the governing principles when the light has internal structure? In this review we will often use scalar and vectorial combinations of light that carries OAM, a highly topical example. Such modes of light have an azimuthal phase profile given by exp(ilϕ), where ϕ is the azimuthal angle and l is the topological charge, for photons with lℏ of OAM. For brievity we will refer to OAM modes by their topological charge, l. What are the selection rules when such complex light fields are used in nonlinear processes? As we will show, the development of nonlinear optics with structure light has produced complex behaviour with some as yet unanswered questions. Further, it is not always possible to find exact solutions for the coupled equations that describe these phenomena. For instance, nonlinear processes of even the second order can generate coupled wave equations whose number increases directly with the number of transverse modes involved.

With suitable approximations (such as the slowly varying envelope approximation and lossless media) the generated field in three wave mixing can take the form

3∂E3(ω3)(r)∂z∝χ(2)E1(ω1)(r)E2(ω2)(r).

Similar differential equations are also derived for each frequency, initially obtaining three coupled differential equations. While these equations were initally derived as plane waves, structured light reveals more intricate interactions. For example, the phases and intensities are all intertwined: reshaping one field can mean completely new dynamics and new structures in all three involved fields. Due to the low conversion efficiency, a characteristic of nonlinear processes, in single-pass geometry we can make use of the non-depletion approximation, where the input fields can be regarded as static and therefore do not change on propagation. These equations show one remarkable feature of nonlinear optics: the nontriviality of the superposition principle. For example, let us associate the generated field E′3(r) with input fields {E′1(r), E′2(r)} and generated field E′′3(r) with input fields {E′′1(r), E′′2(r)}. If now we use as inputs E1(r)=E′1(r)+E′′2(r) and E2(r)=E′2(r)+E′′2(r) it will not follow that E3(r)=E′3(r)+E′′3(r). In this equation, the vector nature of this interaction was omitted for simplicity, but it suffices to say that input fields have the same polarization for type-I and orthogonal polarizations for type-II. Equation (3) describes sum frequency generation (where ω3=ω2+ω1) and, if considered difference frequency generation ( ω3=ω2−ω1), one of the fields ( ω1) would be complex conjugated. For second harmonic generation both fundamental fields would have the same frequency ( ω3=2ω1=2ω2) and the two fundamental fields would be identical for type-I but not necessarily for type-II.

The expansion of these fields into propagating waves in different directions gives us the phase-matching quantity

4Δk=kω3⋅r3−kω1⋅r1−kω2⋅r2.

That ensures that the light generated is through a coherent process and interferes constructively at each wavefront generation. When Δk=0, this is referred to as perfect phase-matching.

Figure 1 highlights a few differences between the linear and nonlinear regimes, the latter illustrated using second harmonic generation as an example. We illustrate that the generated spatial structure is not simply a superposition, but the product of input modes. A consequence is that while the original modes may be eigenmodes of free space, the final mode may not. For instance, as shown in Fig. 1(a), if two OAM modes with topological charges of l=4 and l=−4 combine, then the superposition creates a petal-like structured which is stable in propagation, while the nonlinear process creates a ring-like structure with no OAM, which is unstable in propagation.

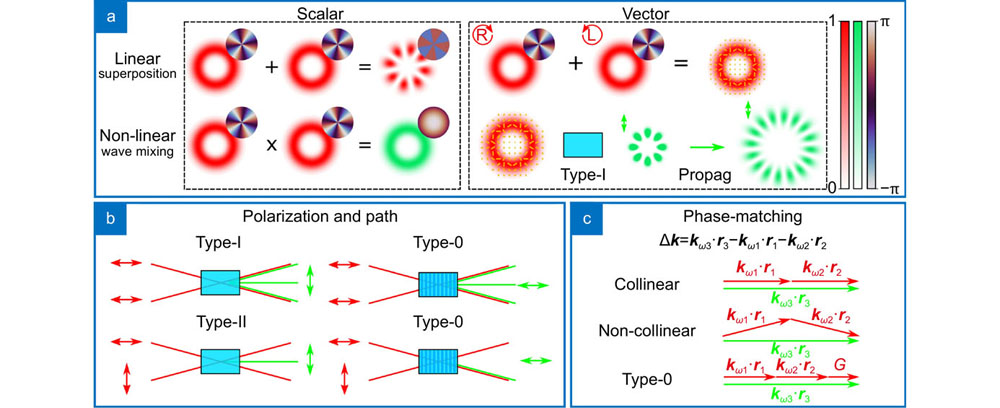
Fig. 1. Linear and nonlinear processes. Using second harmonic generation (SHG), we illustrate the differences between linear and nonlinear processes. (a) Linear processes produce an output mode that is the addition of two input spatial modes of light, while SHG produces the product of the two modes. The linear superposition of two different modes with orthogonal polarization states generates a vector beam, which has a inhomogeneous polarization state. The polarization profile is represented as yellow lines across the transverse profile. In SHG, and wave mixing in general, the polarization profile will dictate where wave mixing happens and thus alter directly the spatial profile. In (b) we show exemplify how path can also be controlled via polarization and the different phase matching conditions of crystals, including the periodic poling of type-0. The mechanism which allows these interactions is sketched in (c). Phase-matching is the condition necessary for wave mixing to occur and exploits birefringence (types I and II) or periodical polling (type-0) to achieve it.

下载图片 查看所有图片

Polarization also has a non-immediate role. In the linear regime, optical beams with orthogonal polarization states do not interfere to produce fringes (but they do produce fringes in polarization^{27, 41}). In contrast, in nonlinear media, they do interact through the coupled interactions with the medium. If the input beam has a inhomogenous polarization profile, i.e. vector beam, then this interaction is different in every point of the transverse profile. We illustrate this in Fig. 1(b) where a vector beam used as input shows that SHG has different efficiencies across the transverse profile. This can be seen as a projection onto one of the crystals axis, generating a beam with a uniform polarization state and its spatial structure is influenced by both polarization and structures of the fundamental beams. This dependency creates states that binds path, input polarization and spatial mode. To understand the connection, one can consider the schematics in Fig. 1(b). The perfect phase-matching condition can be fulfilled for more than one propagation direction at the same time, each as independent processes. The wavevectors in this equation are considered inside the matter (often a crystal), where differently polarized beams would see different refractive indices, crafted specifically to fulfill this condition in types I and II. For type-0, the material is structured with a periodic polling, which gives a contribution of Gm=m2π/Λ to phase-matching where Λ is the domain length.

The combination of Eqs. (3) and (4) exemplifies the role structured light's degrees of freedom (DoF) in wave mixing, encompassing spatial profiles through the coupled wave equations (Eq. (3)), polarization in the phase-matching (both in χ(2) and kx,y,z) and path in the phase-matching Δk. Only by considering all these DoF and their interaction we can grasp a full understanding of nonlinear processes with structured light.

3 Structured dofs and their nonlinear coupling

By choosing sum-frequency generation and breaking wavelength degeneracy, it is possible to encode different structures in each frequency. If one of the fields is physically expanded and thus approximated to be a plane wave, we see the directly transfer and manipulation of the spatial profile of a beam across wavelengths^42-44. In this case, the lack of structure of one field enables the generated beam to completely inherit the structure from the other. By using different spatial modes in each frequency, it was possible to perform OAM algebra⁴⁵. This creates an interesting interaction where the wavelength is used as a control parameter for the spatial structure.

In initial works with SHG it was observed that the generated field would be proportional to the square of the fundamental frequency³⁶, as it is possible to see in Eq. (3) if the conditions ω3=2ω2=2ω1 and E1=E2 are set. This describes type-I phase matching. If the vectorial nature of this interaction with matter is chosen accordingly, it is possible to use type-II phase matching to have different spatial modes in the same frequency but different polarizations^{46, 47}, creating in the SHG a profile composed of the product of two different modes of the same frequency. Even in the collinear geometry configuration, there is an interplay between the spatial and polarization degrees of freedom.

The path degree of freedom can also be used: in Eq. (4) we can see that the phase-matching depends not only on the material but on the propagation direction of the beams. If two beams are crossed inside the crystal so that the phase-matching is fulfilled, a third beam is generated, as illustrated in Fig. 1(c). Using this it was possible to study the transverse structure transfer in SHG⁴⁸ and off axis singularity combination⁴⁹. In these cases (the former is shown in Fig. 2(a)) one input wave can be approximated as a plane wave and the other has nonzero OAM. The non-collinear interaction generates the second harmonic of both input modes with the square of the spatial profile but also creates a third beam with the product of them, having the same OAM as the input, but different polarization and wavelength.

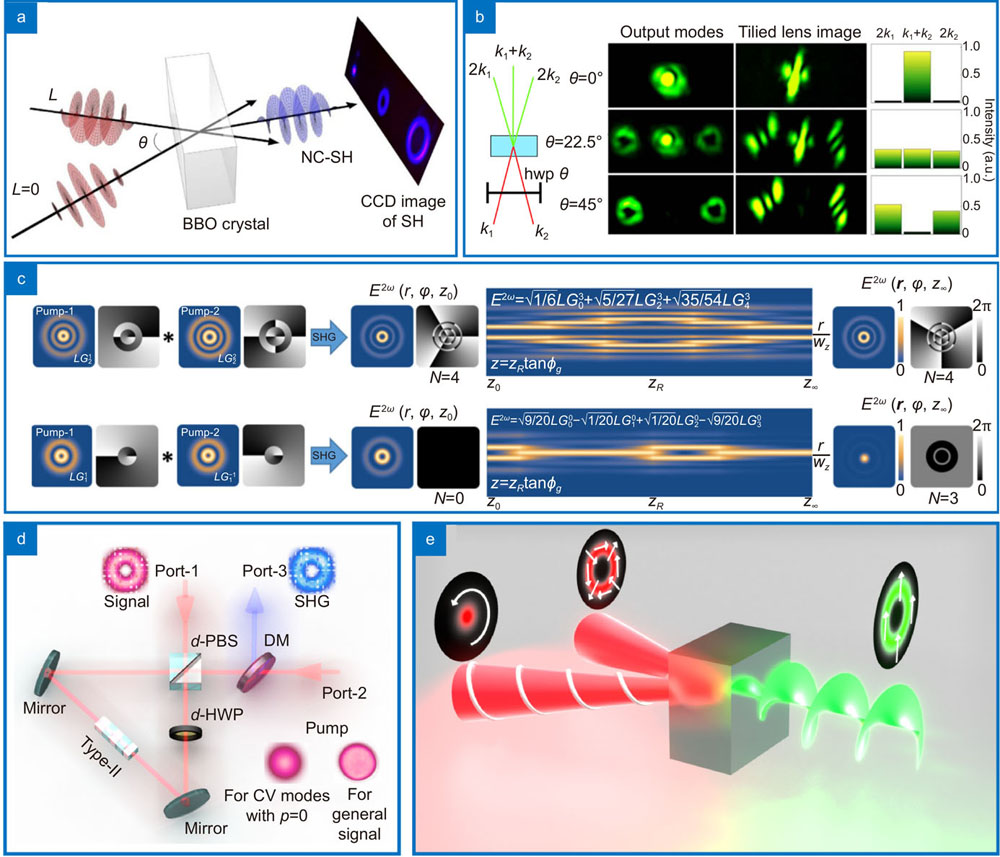
Fig. 2. Wave mixing with different degrees of freedom. In (a), the authors show OAM algebra in noncollinear SHG. When type-II phase-matching is used, the same noncollinear geometry allows for polarization switching, shown in (b). This effectively couples multiple degrees of freedom in a single process: path, polarization, radial and angular transverse structures. The radial selection rules of LG modes in wave mixing are demonstrated in (c). There is a intrinsic relation between the radial and angular degrees of freedom, which is manifested in the propagation dependence of the spatial profiles. In (d), a experimental scheme using a Sagnac interferometer achieves faithful frequency conversion of vector light. Spin and orbital angular momentum are combined in second harmonic generation in (e). Figure repoduced with permission from: (a) ref.⁴⁸, Springer Nature; (b) ref.⁵⁰, © Optica Publishing Group; (c) ref.⁵⁴, © American Physical Society; (d) ref.⁶⁹, American Physical Society; (e) ref.⁷⁰, under aCreative Commons Attribution 4.0 International License

下载图片 查看所有图片

The three process depicted above are independent and do not interfere with each other. Interestingly, not all nonlinear process are independent. Using polarization as a control parameter in type-II SHG, the authors realized that nonlinear process can interfere destructively⁵⁰. As illustrated in Fig. 2(b) two input beams with opposite OAM and orthogonal polarization states pass through a half-wave plate (HWP) at an angle θ and impinge at the crystal with a small angle. When θ=0 the phase matching conditions are only satisfied for one path. For θ=22.5° all three paths have equal phase-matching conditions satisfied and therefore equal intensities. However, when θ=45° the phase matching conditions are satisfied for all paths, but the middle one has zero intensity. This happens because there are two wave mixing process occurring on the same path, but interfering destructively. This interplay between path and polarization enabled an opportunity for all-optical switching.

3.6 Scalar structured light

The fields in Eq. (3) can be expanded in the well known spatial modes, and by using orthogonality relations, the right-hand side of this equation becomes a set of three mode overlap integrals. The modal description of this process has resulted in a important result regarding the interaction of light with matter, for example, the conservation of OAM per photon in classical^{36, 51} and quantum³⁷ nonlinear processes.

Interestingly, the coupling is not only between light and matter, but between differences in structure of the fields themselves, particularly within a given family. For instance, the “untwisting” of the azimuthal phase of an OAM Laguerre-Gaussian (LG) mode in turn altered the radial index^{52, 53}, with the rules governing this interaction only recently unveiled⁵⁴, and shown to be true for wave mixing processes of any order⁵⁵. This intricate relation is illustrated in Fig. 2(c). The first row shows a process where two different radial structures are used as inputs and the state generated ends up as a superposition of different radial orders, up to a mode of order equal to the sum of the input orders. On the second row, the azimuthal phases cancel each other, generating higher radial orders. Similar processes have been observed with Hermite-Gaussian (HG) modes. Here, their separable Cartesian form makes the interpretation of the selection rules far more straightforward, aided further by the fact that they are the natural solutions of the anisotropy of a biaxial crystal⁵⁶, an important aspect in optical cavities. Since these seminal studies, wave mixing with structured light has included Ince-Gaussian^{57, 58} and Bessel-Gaussian^59-62 modes, confirming OAM conservation and exploring the selection rules of these families. OAM conservation was not only shown for integer but also for fractional topological charges^{63, 64}, in an off axis configuration⁶⁵ and even in plasmonic media^66-68. A summary of the different behaviours structured light and its different modes can have in second order nonlinear wavemixing are summarized in Table 1.

One might ask if there is there a recipe for the input to the nonlinear process in order to obtain a desired output structured field? The answer can be trivial, where one or more of the input profiles are plane waves and one of them contains the desired structure. By this approach, LG and HG structured modes have been created, as well as general structured images⁷¹. When this is not possible, the HG basis is suggested to be optimal⁷², and has been used for high fidelity mode generation⁷³. Because wave mixing allows for light modulation by light, the process can be adapted to be used as a detector of structured light^{71, 74, 75}, and has been used to detect LG and HG modes with very little modal cross-talk, in a manner analogous to modal decomposition⁷⁶. Even complex images can be handled in this manner, with the benefit of noise reduction (squaring a signal will amplify the strong and the decrease weak). For this reason, this has been an emerging application of SHG, with demonstrations including augmented edge contrast^{77, 78} and contrast enhancement to improve recognition of human faces and QR codes⁷⁹.

3.7 Vectorial structured light

So far we have considered the case where the structured light is scalar, so that the polarization is homogenous across the field. A complex vectorial structure is achieved by combining orthogonally polarized states such that each has its own unique spatial mode. If the spatial modes are also orthogonal, then the polarization structure of the field will be maximally inhomogeous³. On the right-hand side of Fig. 1(a) we have an example of a vector beam with spin-orbit coupling. Two beams of orthogonal circular polarization states and opposite OAM are combined to form a complex polarization pattern. The yellow lines represent the linear polarization state at every point in the transverse profile at a given angle. Since nonlinear wave mixing depends on both the spatial mode and polarization DoFs, it might seem that a inhomogenous polarization structure would be bound to change when frequency converted. In fact, frequency conversion of vector structured beams has been characterized as producing non-trivial scalar patterns in type-II SHG^{80, 81} and having an altered vector structure when generated in SHG with sandwiched crystals⁸² and using a Sagnac loop⁸³. In this sense, the inhomogeneous state of polarization has been proposed as a control parameter for nonlinear process^{50, 84}. Recently an elegant approach was realized using a Sagnac loop, making it possible to convert a vector beam in frequency^{69, 85, 86} while retaining the polarization structure, as illustrated in Fig. 2(d). Here, one input is a vector beam and the other a auxiliary beam, the latter having a somewhat flat intensity and phase distribution. A polarizing beamsplitter (PBS) is used to separate the vector beam into two components where the loop shape makes them propagate in opposite directions. By inserting a half-wave plate (HWP) in the loop, each component of the vector beam is combined with an orthogonally polarized co-propagating plane wave, which enables faithful frequency conversion of each component independently. Lastly, the same PBS recombines both components back into a vector beam with the same spatially structured polarization but at a converted wavelength. Some observed effects of vector beams in wave mixing process are summarized in Table 1. The examples provided only deal with second order processes. A theoretical approach was already proposed to characterize the full vectorial nature of wave mixing for every nonlinear process order, based on input and output fields⁸⁷, but has yet to be realised.

A peculiar effect observed in the nonlinear regime is phase conjugation, where the generated beam has the conjugate (negative) phase of a impinging beam. The allure of the nonlinear approach is that no knowledge of the initial phase is required for the process, unlike linear phase conjugation that always requires some wavefront sensing and adaptive control. In nonlinear optics this effect was first achieved and historically associated with four-wave mixing, but it has been shown that a second order effect, Stimulated Parametric Down Conversion, can partially achieve it, conjugating the transverse phase structure⁸⁸ but not the propagation direction. It has been demonstrated with scalar⁸⁹ and as well as vector^90-92 beams.

3.8 Spin-orbit coupling

In paraxial optics, the spin angular momentum and the orbital angular momentum of a photon are treated as independent degrees of freedom. But even in this regime, we can find instances of these two quantities coupled. A notable example is a special group of vectorial inhomogeneous beams made of spatial modes carrying different OAM in polarization components carrying SAM. Besides these vector vortex beams, conical diffraction⁹³ has been shown to produce optical vortices in the linear regime depending on the input SAM, effectively coupling them. Conical diffraction is a consequence of birefringence and has been reported to excite second harmonic generation in biaxial crystals^94-96. The combination of conical diffraction with nonlinear process such as second harmonic generation can be combined to create cascaded processes that operate both on OAM and SAM⁹⁷. In this interesting example, the SAM is converted into OAM by conical diffraction, but only partially. The two parts (converted and unconverted) then act as fundamental fields for a SHG process of each state. The resulting beams from this conversion also suffer conical diffraction, having their OAM altered according to their SAM. By starting with a simple Gaussian beam with SAM, the authors show these two DoFs can be strongly coupled even in a simple material. However, these two degrees of freedom, while independent and possibly coupled, can interact in a nonlinear process⁷⁰, as depicted in Fig. 2(e). A spin-orbit coupled beam of OAM lω is combined inside the crystal with another beam only having SAM Sω, resulting in the generation of a beam having OAM l2ω=lω+Sω.

3.9 Intra-cavity dynamics

Lasers are a well known nonlinear device, and here too structured light laser cavities have a long history (see ref.⁹⁸ for a review), with internal frequency generation used extensively for OAM generation⁹⁹ and even with wavelength tuneability¹⁰⁰. While a full review is beyond the scope of this article (see refs.^98-100 for good reviews), we briefly highlight some interesting advances. These include intra-cavity geometric phase¹⁰¹ for helicity control, spin-orbit effects¹⁰² with high purity, vortex OPOs¹⁰³ to move into the mid-infrared, wavelength and OAM tuneable lasers¹⁰⁴ based on fibre geometries. Most of these solutions have been at low power. Nonlinear laser amplifiers have been used to raise the power levels, both in bulk crystals¹⁰⁵ and disks¹⁰⁶ with vectorial light, including parameteric amplification of ultrafast structured light¹⁰⁷, and with scalar structured light in Erbium fibre amplifiers¹⁰⁸ as well as by Raman amplification¹⁰⁹.

Frequency converting cavities for structured light at the source include the use of exotic intra-cavity elements such as spatial light modulators for radial modes¹¹⁰ and metasurfaces for super-chiral OAM modes¹¹¹, with recent work extending to vortex lattices¹¹² and Poincaré beams¹¹³. Nonlinear optical elements are often placed in cavities to enhance the efficiency, but this too can influence modal structure. Nonlinear cavities such as Optical Parametric Oscillators (OPOs) show rich behaviour not seen in free-space propagation. For example, controlling the spatial properties of a Gaussian pumped triple resonant OPO changes its threshold and allows for simultaneous oscillation of several mode pairs with fixed relative phases⁴⁶, and can result in multiple complex patterns^{114, 115}. A thorough study on the influence of the geometrical properties of the OPO on the generated spatial modes can be seen in¹¹⁶ and their applications in continuous variable entanglement in¹¹⁷. The structured output can be tailored by structuring the pump^{56, 118}, as can the geometry of the cavity itself¹¹⁹, making the cavity selective to specific modes.

4 Structured matter for structured light

The nonlinearity we are discussing refers to the interaction of light and matter. The structure of the output light (created or detected) is therefore tailored by both the input light and the medium, allowing the latter to be tailored. This is achieved when the medium higher-order susceptibility is no longer a constant but instead has a space dependency, e.g., χ(2)(r) for the second order term. The structuring of the medium can be a very important tool to shape the outcome of a nonlinear process. We will now present two of the more prominent structured media in the field: crystals and metasurfaces.

4.2 Crystals

In the past this structuring of crystals has been done through acousto-optic modulators, giving rise to effects such as Bragg and Raman-Nath scattering, modulating the refractive index hence the phase matching conditions as well. The modern toolkit includes more direct manipulation of materials (e.g., structured photonic crystal). Phase matching in nonlinear photonic crystals has been well explained and explored^123-125 with periodic poling playing a important role in the past decade¹²⁶, branching into many applications, including a nonlinear version of the Talbot effect¹²⁷. By introducing a carefully crafted spatial modulation in a nonlinear crystal, it was shown to be possible to control the amplitude and phase of the generated fields^128-130. One highlight is the work illustrated in Fig. 3(a) where the authors carefully exploit the inversion of dipole domains to “twist” light as it is created¹³⁰. At any point in the fundamental beam’s spatial profile there is light conversion with the same efficiency, but not the same phase. This phase modulation acts as a medium-enabled nonlinear holography.

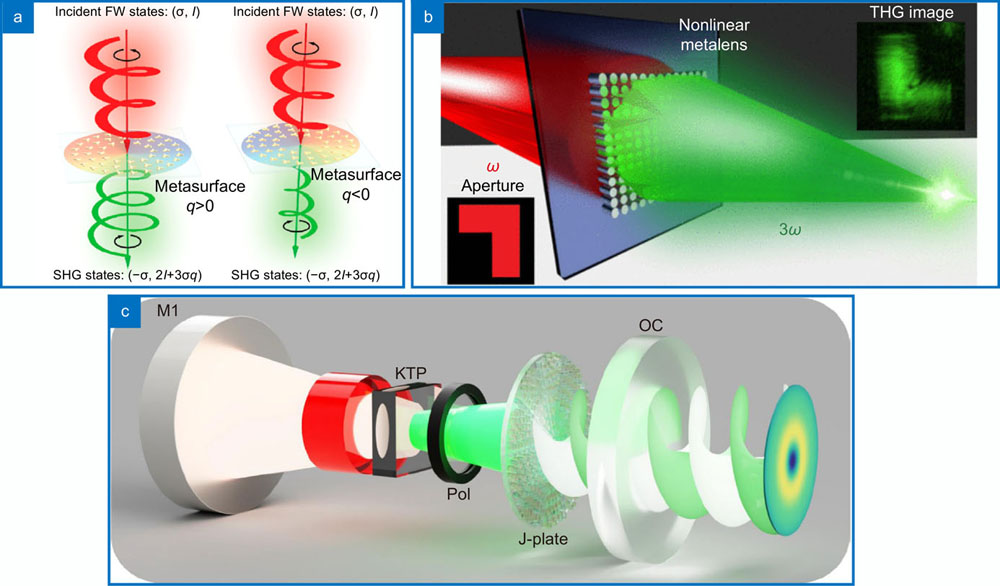
Fig. 4. Nonlinear optics enabled metasurfaces. These devices were shown to enable non-trivial interactions while frequency converting beams. In (a) a SHG process coupling SAM and OAM. The combination of frequency conversion with holography creates metasurfaces with metalensing properties in (b)¹⁴⁴. An application taking advantage of the high damage threshold of these materials can be seen in (c)¹¹¹ where the inclusion of a metasurface inside an optical cavity creates a laser with OAM from the source. Figure repoduced with permission from: (a) ref.¹⁴³, © American Chemical Society; (b) ref.¹⁴⁴, under a Creative Commons Non-Commercial No Derivative Works (CC-BY-NC-ND) Attribution License; (c) ref.¹¹¹, Springer Nature.

下载图片 查看所有图片

The phase-matching conditions involves not only material but also energy constrains. The periodic polling can not only enable frequency control^{131, 132} but when multiplexed it achieves phase-matching for multiple wavelengths in the same crystal¹³³. Recently, a novel pattern in the periodic polling named quasi-periodic polling achieved simultaneous second and third harmonic generation¹³⁴. Further, the structuring of the media is not restricted to one dimension: by using oblique incidence on a periodically polled crystal it was possible to couple mode selection with phase matching¹³⁵, coupling DoFs of light and matter. Photonic crystals can be structured so that phase-matching is crafted in both longitudinal and transverse directions^136-138 so that light is structured as it is generated. A thorough review on this emerging area can be seen in ref.¹³⁹.

An interesting combination of birefringence and periodic polling can be seen in ref.¹⁴⁰, where the spatial macroscopic structure complements the unit cell structure to achieve both type-0 and type-II phase-matching simultaneously. Besides changing the structure itself, changing the orientation of the medium can achieve interesting results. The sandwich crystal configuration (a combination of two identical crystals optically joined but oriented at 90°) has been employed for the frequency conversion of vector light⁸².

As much as the structured of the medium dictates phase-matching, the other way around also happens: we can use this property of the medium from a material analysis perspective¹⁴¹ and use these nonlinear process to characterize crystals according to their symmetry groups¹⁴².

4.3 Metasurfaces

The structuring of the medium is not exclusive to crystals, as metasurfaces have been employed in many areas and nonlinear optics is no exception. They have seen a lot of atention recently by achieving high conversion efficiencies. The nanostructures composing these crafted surfaces are capable of confining light in volumes smaller than the diffraction limit^{145, 146}, greatly enhancing nonlinear effects. Excellent reviews can be found in ref.^{145, 147, 148}. They are structured by definition and can combine wavelength conversion with wavefront control^149-151, spin-orbit interactions¹⁵², OAM operations involving SAM¹⁴³, image encoding¹⁵³ and optical activity¹⁵⁴. Two illustrative cases can be highlighted: OAM-SAM interactions¹⁴³ and metalensing¹⁴⁴. By creating gold meta-atoms with three-fold symmetry, the authors in ref.¹⁴³ arranged the metasurface to enable azimuthal geometric phase and frequency conversion at the same time, creating devices depicted in Fig. 4(a) that operates on both SAM and OAM. In the second one, illustrated in Fig. 4(b), the authors combine a novel technique that exploits Mie ressonance in all-dielectric metasurfaces and third harmonic generation. The phase of the generated wave inherits a metalens profile from the medium structure. This results in a process that illuminates an aperture with light of a given wavelength and then, after passing through the metasurface, it is converted to its third harmonic and imaged at a focal point. All in a flat and compact optical component. The development of metasurfaces has allowed tremendous growth in nonlinear optics, not only because of their high efficiency, but their fabrication process being scalable and the high damage threshold needed for laser sources integration. In ref.¹¹¹ the authors demonstrate how a metasurface placed inside a laser cavity can generate high purity OAM modes from the source, depicted in Fig. 4(c).

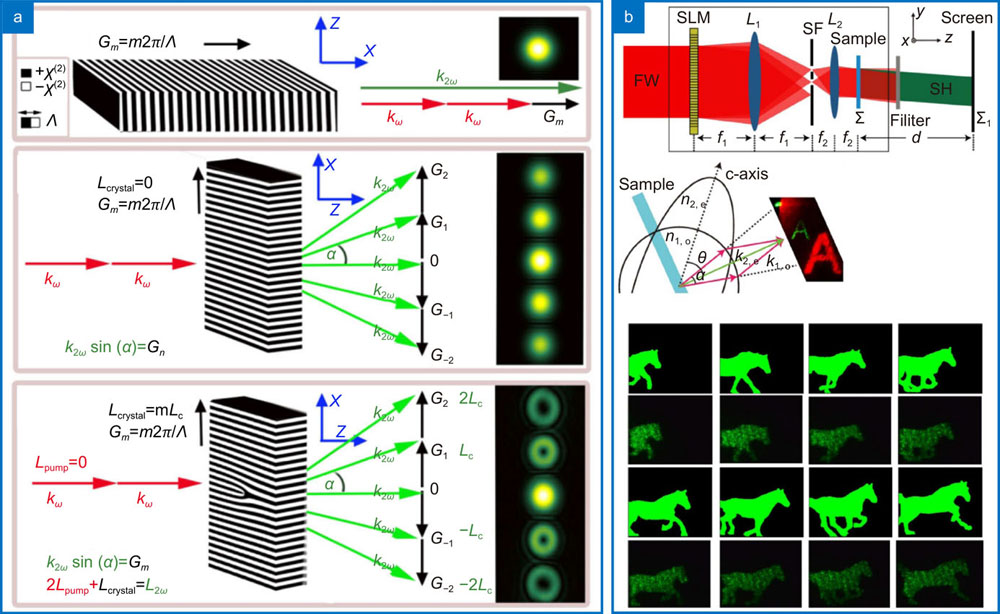
Fig. 3. Nonlinear Holography. In (a) the structuring of the medium is illustrated: the fundamental field is always the same, but the medium is not. The selective inversion of the electric domain across the transverse plane creates different spatial structures in the second harmonic field. The periodical transverse structure is responsible for multiple phase matching mechanisms, both longitudinally and transversely. In (b) it is shown how non-collinear SHG can transfer a specific intensity pattern from one wavelength to the other. First row shows the imaging arrangement and the second column shows the phase-matching conditions and an example of output modes. Right below is a experimental demonstration that this can be used for real-time frequency conversion of computer generated holograms. Figure repoduced from: (a) ref.¹³⁰, © American Physical Society; (b) ref.¹⁵⁸, © Optica Publishing Group.

下载图片 查看所有图片

5 Nonlinear holography

Since very early in the study of nonlinear optics, it was understood that wave mixing meant modulation and that this could be used for holography¹⁵⁵. In the original version, the counter-propagating fields involved in the four-wave mixing formed a grating that changed the generated field. Nowadays, we have more advanced forms of holography. When looking at Eq. (3), it is clear that all fields involved in wave mixing influence each other in amplitude and phase. But more importantly, it has come to a collective understanding: the optical field involved in wave-mixing can be seen as diffracted by the other involved fields. Going back to Eq. (3) we can set E1(ω1) to be a plane wave and E2(ω2) a diffraction pattern, both in a non-depleting regime happening only at a single plane in propagation. This would generate a field E3(ω3) not different than a simple plane wave passing through the same diffraction obstacle.

In this sense, by shaping the fundamental beam as a hologram it is possible to modulate the generated beam as it is created¹⁵⁶. This process allows for holograms that are self adaptive and depend on the generating fields, being able to copy or regenerate optical modes¹⁵⁷, even complex patterns in real time¹⁵⁸. In this example, illustrated in Fig. 3(b), the authors generate a hologram and the light affected by it is filtered in the Fourier domain. Only the first order, containing the intended pattern, and the zero-th order, containing a Gaussian profile, are selected. Those are used as inputs for non-collinear SHG, and the result in the intermediate path is the frequency conversion of any pattern encoded in the hologram in real time. The authors demonstrate this by encoding the holograms with frames of a movie of a running horse in a infrared laser and detecting the same frames on the visible green light.

If the interaction happens in more than a single plane, i.e. the medium is longer than a diffraction length, these approaches can be extended to three dimensions for volume holography^{159, 160} in nonlinear crystals, and the reader is referred to refs.^161-163 for excellent reviews on this topic.

6 Four-wave mixing

As we consider higher-order nonlinear effects, wave-mixing becomes increasingly complex. For example, OAM conservation in a four-wave mixing (FWM) process with third order nonlinearity was observed in cold cesium gas in ref.¹⁶⁴ where only one beam was structured with OAM, resulting in the transfer of OAM to the generated beam and similarly with modal superposition¹⁶⁵. This was later expanded to include both probe and pump having OAM^{166, 167}, where the phase matching conditions can be fulfilled in more directions than lower order process and this results in the creation of a higher number of states created in different paths, as depicted in Fig. 5(a). Beyond OAM, a hot atomic vapour of ⁸⁵Rb was used to generate Bessel beams from Gaussian pumps by careful control of the phase matching¹⁶⁸. With the same medium, a multimode four-wave-mixing process was established with two pump beams of the same frequency that crossed at a small angle, producing three photons that are highly correlated and could be applied to multipartite entanglement distribution¹⁶⁹. The idea exploited the simultaneous fulfillment of two phase matching conditions that reinforce one another.

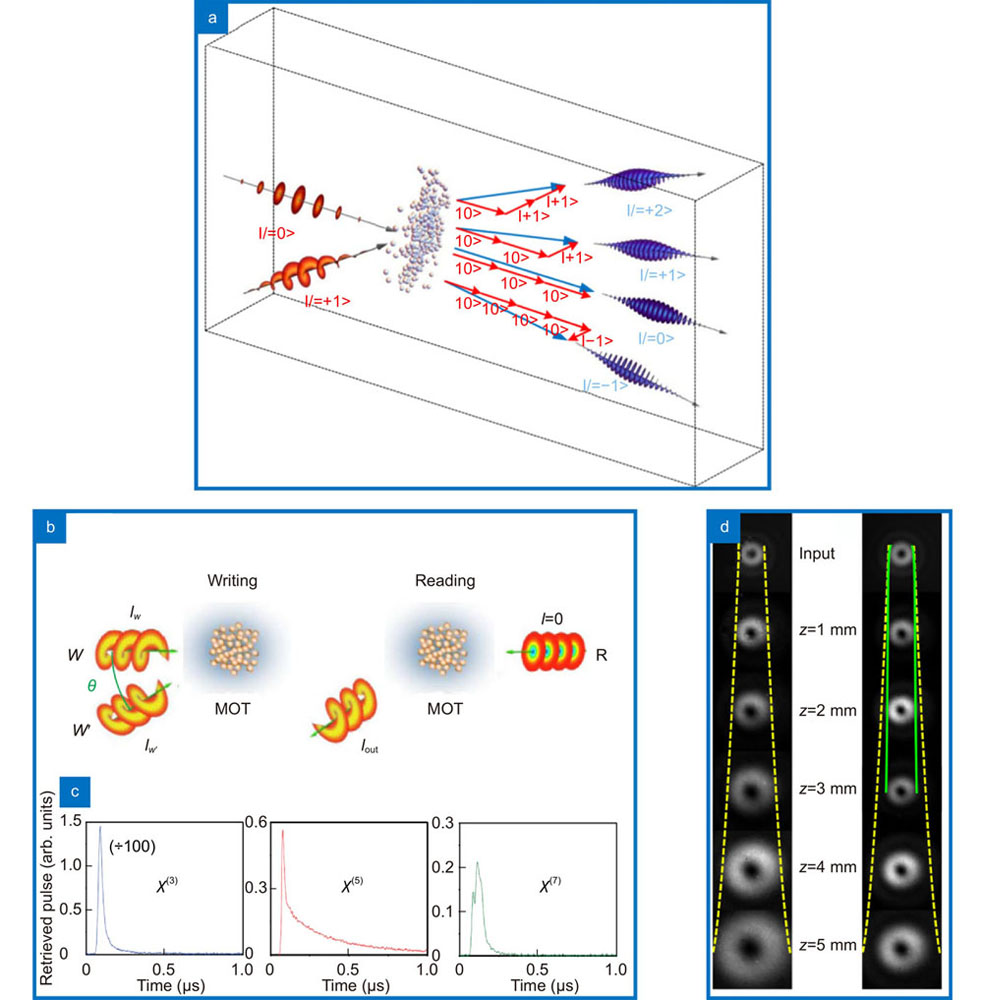
Fig. 5. Higher order process. In the generation of high harmonic orders, it is possible to generate beams of many different OAM from just two different inputs, as depicted in (a). The process of writting and reading optical memory is depicted in (b) and the diference in time scales depending on the order of the nonlinear process in (c). In (d) it is demonstrated robust self-trapping of a bright vortex beam by exploiting higher order nonlinearities of odd orders. Figure repoduced from: (a) ref.²⁰⁹, Springer Nature; (b) ref.¹⁹¹, © Optica Publishing Group; (c) ref.¹⁹², © Optica Publishing Group; (d) ref.²⁰⁴, © American Physical Society.

下载图片 查看所有图片

Using a long medium approximation, radial and angular mode conversion by FWM in a heated Rb vapour was demonstrated, making evident the role of the Gouy phase-matching in this regime¹⁷⁰. Beyond just spatial DoFs, the spatial and temporal DoFs are not independent in this process¹⁷¹, where frequency control enables selection of various spatial modes as outputs.

Recent developments with dielectric materials have been shown to enable four-wave mixing with high efficiency. These materials have been crafted in the nanoscale as plasmonic nanoantennas^{172, 173}, metasurfaces^145-148, nanodisks¹⁷⁴, enabling not only frequency conversion to a wider range of wavelengths but the intrinsic structure also motivated simultaneous wavefront shaping¹⁴⁴.

7 High-harmonic generation

High-harmonic generation (HHG) is an extreme process, not regarded as perturbative process and cannot be represented in Eq. (2). This can be seen phenomenologicaly by the fact that all harmonics generated have comparable efficiencies, unlike parametric frequency conversion. Instead, HHG is defined by the ionization of the medium: light impinging in a medium is strong enough that it perturbs an electron bound to an atomic system to the point where it escapes its bounding potential. When this electron is recaptured by an identical atomic system, it liberates the kinetic energy stored, emitting a photon of an energy many times the absorbed ones. This description is known as the recombination model¹⁷⁵. The different underlying physics makes this process still a mystery to be studied in the context of structured light interaction with matter. In recent years, there has been considerable progress tackling this problem. One might wonder if OAM would be conserved or how SAM would affect this process. A few studies observed that the polarization of the impinging light can be controlled¹⁷⁶ even at isolated pulses timescale¹⁷⁷. Regarding the spatial structure, some previously unseen behaviour was demonstraded. When using optical phase vortices, OAM operations happen periodically (along harmonic order)¹⁷⁸. Analogous to phase matching conditions in a non-collinear parametric process, it was possible generate many other beams with just two inputs having differing OAM¹⁷⁹, demonstrating OAM algebra. Not only the azimuthal degree of freedom was studied, but the radial structure was also studied in ref.¹⁸⁰ to show its dependency on the atomic dipole phase. An exciting application is the control of generated spectral domain via structuring the pump to generate an effective blazed active grating in gases^{181, 182} and the generation of autofocusing intense beams¹⁸³. While these studies were done separate, others show that these two DoF are not independent in this process and use polarization as a control parameter of this process^{184, 185}. Since the output was made of many different frequencies with different OAM, this effect was characterized as producing Spatio-Temporal vortex in extreme UV¹⁸⁶ and even self-torque, a behaviour previously not seen in light¹⁸⁷.

8 Space-time coupling

The medium cannot interact instantly with light: first, structured light interacts with a medium that inherits this structure momentarily. When the first light source is no longer there, a second light source interacts with the medium and inherits the structure of the first one. This effect is known as optical memory and is regarded as a possibility for storing quantum information in a multi-dimensional state space. A demonstration of this principle was observed in ref.¹⁸⁸, where light interacting with an atomic system (cold cesium gas) induced by a coherence grating lead to OAM conservation, a first step towards the demonstration of optical storage. This spatially dependent coherence transferred to the medium was shown be maintained in time¹⁸⁹, reporting storage times of up to 100 μs. It was shown in ref.¹⁹⁰ that it is possible to store OAM in the same system and also retrieve it by employing Bragg diffraction. The same effect was also achieved in ref.¹⁹¹ but exploiting a different effect: coherent population oscilation, which uses the long relaxation time of the ground state of an open two-level system to store information carried by a light field. This process is depicted in Fig. 5(b), where a writting stage is the interference of two beams carrying opposite OAM inside the medium. The reading stage is a Gaussian beam that enters the medium and exits with information from a beam which was no longer there. In Fig. 5(c) it is shown that different nonlinearity orders exhibit different time signatures, which can be used as a control mechanism¹⁹². Advancing on the path of long lived optical memory storage, by exploring electromagnetic induced transparency, in ref.¹⁹³ the authors were able to execute OAM storage and retrieval as a reversible process in single photon level.

While the process described above couples a specific structure to another during a time window, there are light structures that are notorious for having its time and space non-separable: the spatiotemporal optical vortices^{14, 194}. These beams exhibit OAM transverse to propagation direction, instead of usual longitudinal OAM of phase vortex beams. One might wonder if these space-time structures would hold in the nonlinear regime. Recent works showed that in SHG the spatiotemporal OAM is also conserved^{195, 196}, while also reporting effects such as time astigmatism and singularity splitting due to group-velocity dispersion.

9 Spatial solitons

The self-focusing action of a medium can balance precisely the diffraction of a beam, resulting in the creation of optical solitons. The first observed optical solitons were dark vortex solitons, which are phase vortices that propagate in a self-defocusing medium with third order nonlinearity χ(3)<0¹⁹⁷. This means that the beam modulate itself, with a defocusing effect shaped across the transverse plane by the intensity profile. The dark central of a vortice would naturally increase due to propagation, but a self-defocusing effect in the bright regions would redistribute the intensity of the ring back to the center. The balance of these two process creates a dark soliton: a dark region that does not diffract in propagation.

On the other hand, bright phase vortices suffer from azimuthal modulation instability in self focusing media, which results in their splitting and thus, were hard to be observed. This type of instability in the transverse modulation is similar to one responsible on the filamentation of beams and generation on trains of optical solitons¹⁹⁸.

However, by using non-centrosymetric metal-dielectric nanocomposites, higher-order nonlinear effects such as fifth and seventh order become dominant and cause self-phase modulation^{199, 200}. This ultimately allowed for the observation of stable bright vortex solitons in ref.^201-204. In Fig. 5(d) this is illustrated in two columns: lower intensity (left) and higher intensity (right). For lower intensities, the natural diffraction of the beam propagation happens as usual as the beam size increases in propagation. For higher intensities, the beam size stays roughly the same in a short propagation distance inside this medium. This happens because the self-modulation effect is caused by nonlinear polarization of odd orders which alternate in sign. The lower orders can saturate, so by increasing intensity, the higher orders nonlinear effects becomes dominant and balances defocusing with focusing. For more detailed information, excellent reviews are found in refs.^205-208.

10 Quantum regime

Nonlinear processes have long been associated with quantum optics as the source of entangled photons. The most common source of entangled photons is Spontaneous Parametric Down Conversion (SPDC)²¹⁰, a nonlinear process at its core. By harnessing entanglement and the transverse structure of the photons it is possible to increase the dimensions of quantum protocols⁶. This is often achieved by post-selecting a particular state, the choice of which affects the bi-photon entanglement spectrum in both its shape and dimensionality. This was first realized using OAM³⁷ and subsequently many transverse structures were studied^211-215, as well as inhomogenously polarized beams^{92, 216} and multi-path schemes^{217, 218}. Soon after it followed that it was possible to engineer the pump profile to manipulate the bi-photon spectrum and generate a entanglement spectrum straight out of the source^219-223. Beyond nonlinear optics for creation, the detection and control of quantum states by nonlinear processes has been far less studies, and very much in its infancy.

Although quantum technologies have experienced rapid development in recent years, with light playing a key role, this has mostly been restricted to linear optical solutions, e.g., the ubiquitous beam splitter. For optical systems, a photon-photon interaction in vacuum is not possible. While this is partially true in matter as well, we observe in the nonlinear regime a photon-photon interaction mediated by the medium. Unfortunately this interaction is very unlikely to happen, but it does not mean impossible as this mixture have seen important advances recently (see ref.²²⁴ for a good review), with the building block of single photon wave mixing²²⁵. Nonlinear optics have been suggested in various quantum processes^226-229 and even used for Bell filters²³⁰ for polarization, entanglement swapping²³¹ and a quantum repeater device^{232, 233}. Only recently has structured light entered the equation, with a nonlinear version of spatial teleportation demonstrated with up to 10 modes, overcoming the significant hurdle of ancilliary photons and settting a new state-of-the-art of 10 dimensional teleportation²³⁴.

11 Conclusion

In this review we have touched many topics regarding nonlinear optics with structured light. Unlike linear optics, which generally act on only one degree of freedom, these process have the intriguing feature of coupling many DoFs through the properties of the medium. The possibility is for compact solutions for the creation, control and detection of structured light, yet many open questions remain: what structures can we create? How can we transfer structures within and between DoFs? What is the exact input one would need to generate a specific desired output? These questions are still open even in the lowest order of wave mixing. As new light-matter interactions are discovered in the nonlinear regime, it is exciting to see how their structures couple and what insights can be deduced.

From real time holographic transmission to optical memory effects, from bulk crystalline media to sparse gas jets, there are many physical phenomena that are nonlinear optical processes. The development of new materials, techniques and interactions, alongside ever more powerful laser sources, all signal an exciting future for nonlinear control of structured light, and structured light control of nonlinear processes.