1. Introduction

Imaging of the 3D location and dipole orientation of sparsely distributed point emitters gives insights into a range of biological structures, chemical processes, and molecule-level bindings inside cells^[1–6]. The ability to localize point emitters with 10 nm-order precision has aided optical microscopes to resolve features beyond the resolution limit. Rapid development of localization-based superresolution microscopy over the past two decades has stimulated the emergence of many imaging configurations and engineered point spread functions (PSFs) to achieve 3D localization, better spatial resolution, larger depth of field, faster image acquisition, higher photon efficiency, etc.^[7–12].

The desire for detecting the emitter’s orientation in the meantime originates from the problems associated with localizing more rigidly attached label fluorophores, which cannot be treated as ideal point emitters. Their emission pattern resembles that of an oscillating electric dipole, in contrast to the isotropic emission pattern in most scenarios of localization microscopy, where the emitters are flexibly attached to the structure of interest and can wobble freely. The orientation of anisotropic fluorophores can induce errors when estimating their positions with PSF model functions that do not match experimental data^[1,13].

Single-molecule orientation microscopy (or superresolution polarization microscopy) tackles this problem by measuring the polarization components of the collected light to determine the dipole orientation of the emitters. On one hand, this helps minimize the orientation-induced errors in localization microscopy; on the other hand, one gains access to the anisotropy of underlying biological structure with this additional emitter orientation information. A number of techniques have been introduced for simultaneously measuring the 3D positions and orientations of rotationally constrained emitters and providing superresolved images^[2,13–17]. However, existing techniques typically require polarization splitting in dual-channel configurations, which are often bulky and require complicated calibration.

In this work, we propose a polarization-sensitive helical PSF based on geometric phase that is engineered to yield four lobes (i.e., two pairs). Each pair of lobes forms a double-helix PSF, and the two pairs exhibit opposite z-dependent rotations and opposite circular polarization states. Therefore, one can determine simultaneously the 3D position and the dipole orientation of point emitters from a single snapshot image by measuring the PSF rotation angle and the relative intensity of the two pairs of PSF lobes. This technique allows for a robust and compact single-channel configuration and an achromatic PSF. It utilizes both circular polarization states, yielding nearly 100% photon efficiency. This is vital in photon-starving single-molecule imaging applications, outperforming phase modulations introduced by optical path difference via liquid crystal spatial light modulators.

2. Methods and Results

2.1. PSF engineering using geometric phase

To achieve single-snapshot 3D particle localization, engineered PSFs are typically used on a microscope that employs a phase mask in its pupil plane. The PSF in the image space is therefore expressed as the Fourier transform of the modulated pupil function^[18,19], PSF∝|F{A(r,ϕ)e2πi[ΔΦ(r,ϕ)+D(r,z)]}|2,(1)where (r,ϕ) are the normalized pupil coordinates, A(r,ϕ) is the pupil amplitude, ΔΦ(r,ϕ) is the phase term introduced by the phase mask, D(r,z)=zλ−1n2+NA2r2 describes the defocus phase that occurs when the emitter is displaced by z from the focal plane, n is the refractive index of the medium, and λ is the wavelength of light.

To add polarization sensitivity to the engineered PSF, we utilize geometric phase in the microscope pupil function. Geometric phase is a result of the spin–orbit interaction of light as it propagates through an anisotropic medium, such as liquid crystals^[20,21]. As in Eq. (2), the output field passing a geometric phase element yields the residual light component (first term) and the modulated light component (second term). The former shows the same polarization as the incident light; the latter exhibits an opposite circular polarization state (χ∓) as the incident light and an additional geometric phase term. The magnitude of the geometric phase is generally proportional to the orientation angle of the effective local optical axis α(r,ϕ) and exhibits a polarization-dependent sign. When using liquid crystals, α is the orientation of the local fast axis at (r,ϕ), Eout=cosΓ2Ein+isinΓ2e±i2αχ∓.(2)

The relative intensity of unmodulated light and modulated light is determined by parameter Γ=2π(neff−no)d/λ, which is a relative phase retardation resulting from the birefringence of the liquid crystal^[21]. When Γ is designed as (2k+1)π with k being an integer, the unmodulated light can be completely eliminated, with the modulated light reaching maximum intensity.

In this way, the incident light is spatially modulated and, at the same time, decomposed to left-handed circular polarization (LCP) and right-handed circular polarization (RCP). We can design the local optical axis distribution α(r,ϕ) as half the desired phase modulation to achieve PSF engineering for our purpose. Since α does not depend on the wavelength of light, achromatic PSF can be achieved, outperforming traditional techniques using a dynamic phase.

2.2. Decoding depth information

Assume the incident light is linearly polarized and α=12ΔΦ is designed as half the double-helix phase modulation; we get two opposite phase modulations for LCP and RCP, which generate two mirrored double-helix PSFs following Eq. (1). Each exhibits depth-dependent rotation but in the opposite direction. Thus, this allows us to estimate the 3D position of the point emitter from their mutual center and their rotation angles, and to determine the polarization components of its fluorescence from the relative intensity of the two pairs of PSF lobes.

Figures 1(a) and 1(b) show a simulation of the proposed geometric phase helical PSF in comparison with the diffraction-limited PSF at various axial positions. The pair of “green” lobes is formed by light of LCP, while the “magenta” lobes are formed by light of RCP. It is evident that all PSF lobes rotate around a common center as the defocus changes. The two pairs overlap at the focal plane (z=0), but they do not interfere with each other due to the orthogonal polarization states. An illustration of the 3D intensity distribution of the proposed PSF is shown in Fig. 2, where we can observe the helical propagation of both components. The diffraction-limited PSF profile expands dramatically as defocus increases, yielding a low signal-to-noise ratio at large defocus; in addition, it exhibits the same profile on both sides of the focal plane, resulting in a sign ambiguity when deducing the depth information. In contrast, the helical PSF does not suffer from the above-mentioned shortcomings. In spite of its slightly larger lobe size compared to the in-focus Airy disk, its spatially rotating property leads to a relatively compact profile over the whole depth range of interest.^[7,9]

Fig. 1. Numerical simulation on a 0.75 NA imaging system over a depth range of 6 µm. (a) Diffraction-limited PSF; (b)–(d) geometric phase helical PSF of different lobe separation and rotation rate, with parameter L = 7, 11, and 14, respectively, and ϵ = 0.9. L1, L2 are labels for the LCP lobes and L3, L4 are labels for the RCP lobes.

下载图片 查看所有图片

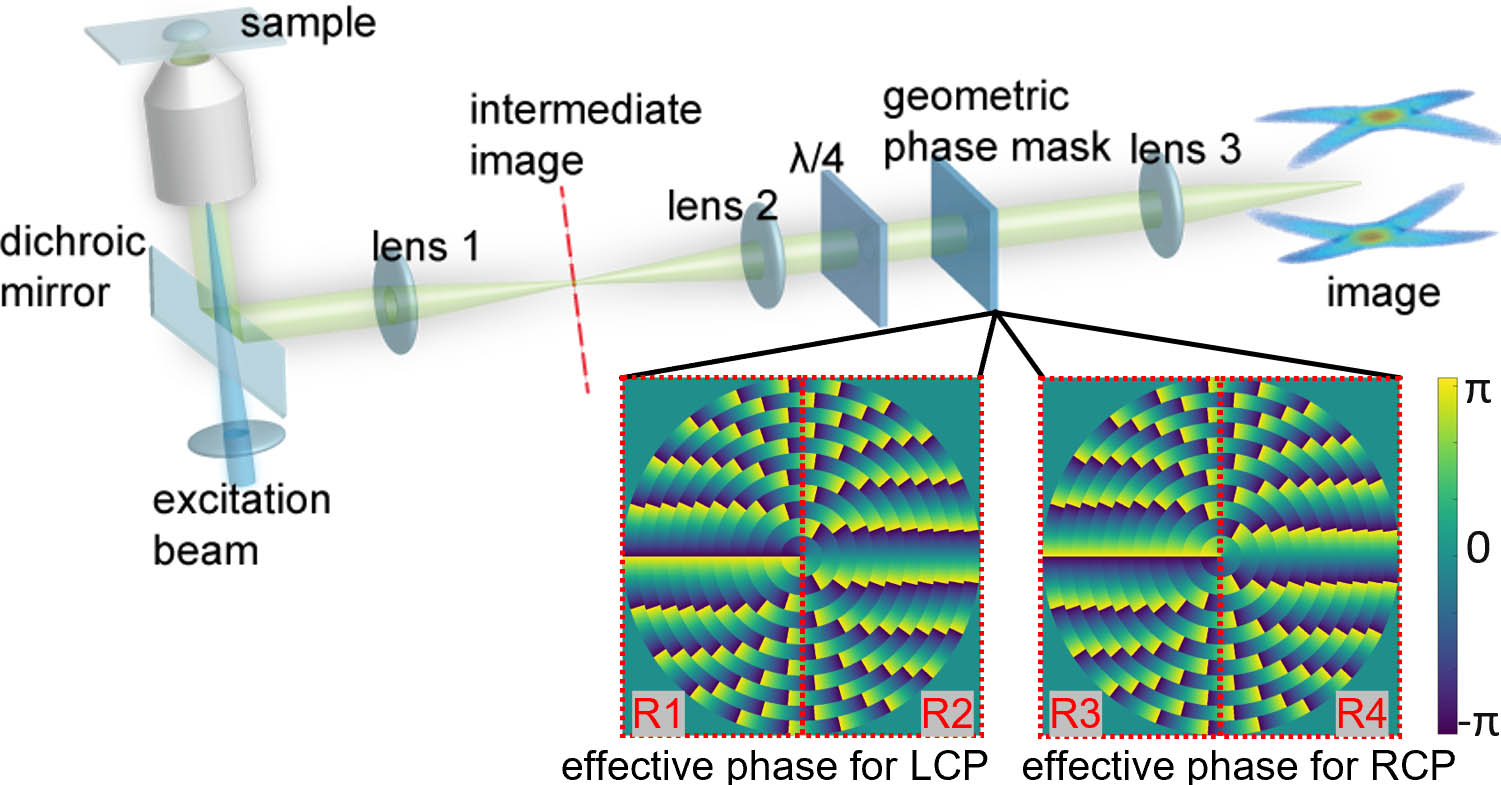
Fig. 2. Experimental configuration. A 4f system is used to access the back focal plane of the objective where a geometric helical phase mask is placed. NA, 0.75; overall magnification, 60×. Focal length of lens 1, 200 mm; focal length of lenses 2 and 3, 300 mm. The phase mask generates opposite modulations on the LCP and RCP light. The two effective phase masks are divided into four regions (R1, R2, R3, R4), which account for the four lobes in the PSF.

下载图片 查看所有图片

Note that in our analysis and experiments, we utilize the Fresnel-zone-based^[9,22] design for the double-helix phase modulation, which was defined on the Fresnel zones as ΔΦ(r,ϕ)=(2l−1)ϕ,(l−1L)ϵ<r<(lL)ϵ,l=1,…,L,(3)where L is the number of angular Fresnel zones with l referring to the l-th zone. ϵ is a parameter that determines the helix peak confinement and the shape invariance during rotation^[9]. A larger L leads to a larger lobe spacing and a slower angular rotation rate, and thus a larger operable depth range. Figures 1(b)–1(d) correspond to PSFs generated with L=7,11,15, respectively. Depending on the sample thickness, the operable depth range may be adjusted by changing L or the numerical aperture of the objective. The resultant ΔΦ is shown in Fig. 2. Two opposite phase functions are illustrated because the geometric phase mask yields opposite phase modulations for LCP and RCP. The phase functions are marked as four regions (R1, R2, R3, R4), which correspond to the four lobes (L1, L2, L3, L4) in Fig. 1. The phase function has rotational symmetry of order 2, considering that ΔΦ(r,ϕ)±2π and ΔΦ(r,ϕ) are effectively the same phase function.

We demonstrate this method on a microscope with 0.75 numerical aperture (NA), 60× magnification by imaging 200 nm-diameter fluorescent beads with an emission peak at 520 nm. As shown in Fig. 2, a 4f system was employed to access the Fourier plane where the geometric phase mask with phase pattern ΔΦ was placed. The mask was custom-fabricated via direct-laser writing^[23], i.e., using a polarized laser to rearrange the fast-axis orientation on a liquid crystal substrate to a resolution of 1000×1000pixels.

Using a piezo stage to scan an emitter along the optical axis, images at various depths were captured, as shown in Fig. 3(a); these correspond to those in the numerical simulation in Fig. 1(c). One can see that our experimental PSF intensity profiles are very consistent with the simulations. The LCP and RCP components of the PSF were filtered experimentally, as shown in Figs. 3(b) and 3(c), where we can see their opposite z-dependent rotations. Note that with isotropic emitters, the intensities of the two PSF pairs are the same.

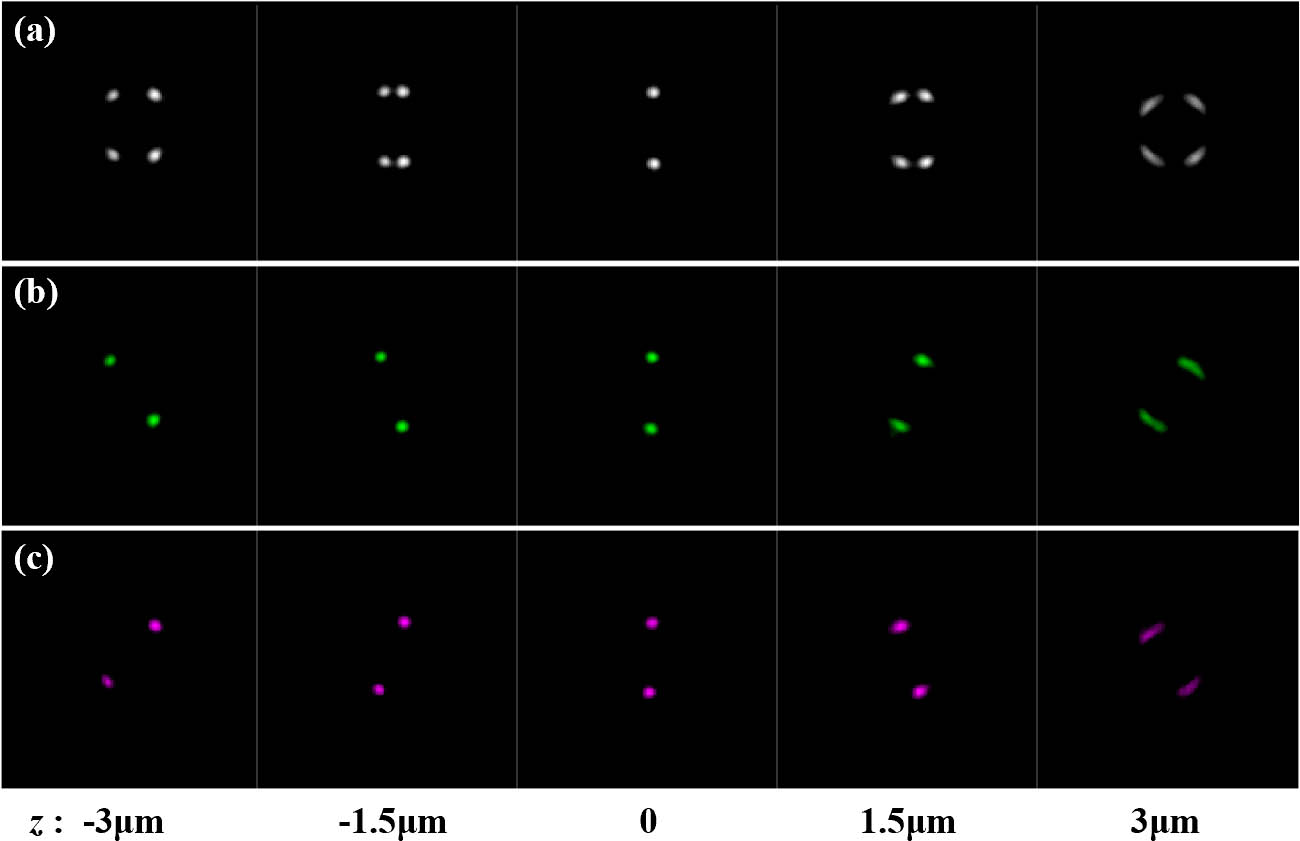
Fig. 3. Experimental image stacks of the geometric phase helical PSF over a depth range of 6 µm. (a) Total intensity; (b) with RCP filtered out; and (c) with LCP filtered out.

下载图片 查看所有图片

We fit multipeak Gaussian profile to the experimental PSF using the least-square method to find the centroid of each lobe (xi,yi), from which the lateral coordinates of the point emitter and the PSF rotation angle can be deduced. Once PSF rotation is precalibrated with respect to the emitter’s axial coordinate, it is possible to calculate emitter’s 3D spatial coordinates from a single snapshot image. Figure 4 shows the calibration data of PSF rotation. A linear relationship was obtained, as expected, over the investigated depth range of 4 µm. It is evident that LCP and RCP yield opposite rotations, with the fitted rotation ratio being 12.9 and 13.2 deg/µm, respectively.

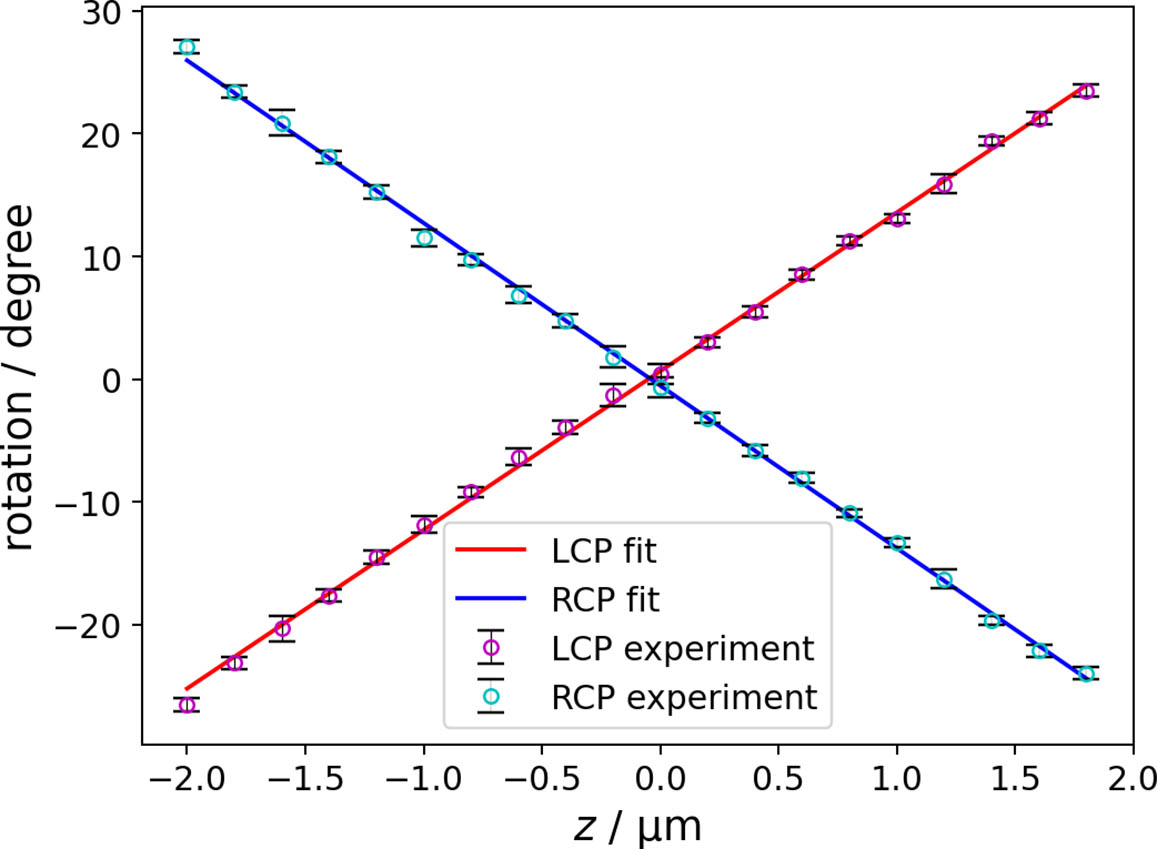
Fig. 4. Calibration data for the geometric helical PSF rotation over a depth range of 4 µm. Two circular polarization components are plotted with magenta and cyan scatters being the experimental data, red and blue solid lines being the linear fit.

下载图片 查看所有图片

Two problems need to be addressed with the above helical PSF design. (1) Due to the symmetrical PSF profile, there is ambiguity in determining the sign of defocus and in differentiating the two circular polarization components. (2) Despite the fact that χ± are orthogonal polarization states and the two pairs of PSF lobes do not interfere, overlapping PSF lobes near the focal plane still present challenges in data processing (i.e., extracting the x, y, and z coordinates).

These problems can be eliminated by downgrading the symmetry in the PSF intensity profile. For example, an additional linear term Φshift in α [as in Eq. (4)] gives rise to opposite lateral shifts in LCP and RCP components, thus separating them spatially. Figure 5 shows two example designs of the shifted helical PSF; false color shows the LCP and RCP, respectively. In the first case, ΔΦshift=cy, yielding a constant vertical shift in the image, with the LCP lobes shifted downwards and RCP lobes shifted upwards. In the second case, ΔΦshift=cx, i.e., the PSF shift is along the x direction. These designs enable the measurement of both the PSF rotation and the intensity of two polarization components over the entire depth range without ambiguity, α=12ΦPSFeng+Φshift.(4)

2.3. Decoding orientation information

Geometric-phase-based PSFs inherently provide the circular polarization components of the incident light; by measuring the light intensity from corresponding PSF lobes, one can directly determine the ratio between the intensity of the LCP and the intensity of the RCP. For deduction of linear polarization components, a quarter-wave plate can be implemented between lens 2 and the geometric phase mask to aid the calculations.

Fig. 5. Asymmetric designs of the geometric helical PSF. (a) LCP and RCP with opposite shifts in the y direction; (b) LCP and RCP with opposite shifts in the x direction.

下载图片 查看所有图片

Assume a linearly polarized incident light of angle θ with respect to the fast axis of the quarter-wave plate. The polarization states after the quarter-wave plate can be written using the Jones matrix, as in Eq. (5). Decomposing the light field to LCP and RCP gives the corresponding light intensity after the geometric phase mask (and the intensity in corresponding PSF lobes), $$\begin{gathered} M14λR(θ)Lx=(100−i)(cosθ−sinθsinθcosθ)(10) \\ =(cosθ−isinθ)=cL2(1i)+cR2(1−i). \end{gathered}$$(5)

Solving the above equation, we have $$\begin{gathered} cL=12(cosθ−sinθ), \\ cR=12(cosθ+sinθ), \end{gathered}$$(6)where cL2 and cR2 correspond to the normalized intensity of LCP and RCP, respectively, from which the orientation θ of incident light can be deduced.

Figure 6 shows the experimental results demonstrating the relative intensity variations in the PSF lobes as incident light changes its polarization direction. The upper-left lobe and lower-right lobe form the LCP helical image, while the other two lobes form the RCP image. The red and blue dots in Fig. 7 show their measured intensities. The intensities are the photon sum of related pixels, normalized to the total intensity to minimize the influence of fluorescence bleaching. When the signal light is polarized in (or orthogonal to) the direction of the quarter-wave plate fast axis, the LCP and RCP lobes exhibit the same intensity. As the incident light changes its orientation, the relative intensity of the LCP and RCP lobes varies, following Eq. (6). Solid magenta and cyan lines show the theoretical curves. It is evident that the experiment agrees well with theoretical predictions, proving that geometric-phase-based PSF can deduce both the 3D position and the incident light polarization orientation without splitting into multiple imaging channels. Therefore, it shows great potential for orientation and localization microscopy of single molecules.

Fig. 6. (a) Experimental results showing the variations in the PSF profile as the incident light changes its polarization orientation; (b) corresponding incident light orientation (note that the fast axis of the quarter-wave plate is along the vertical direction).

下载图片 查看所有图片

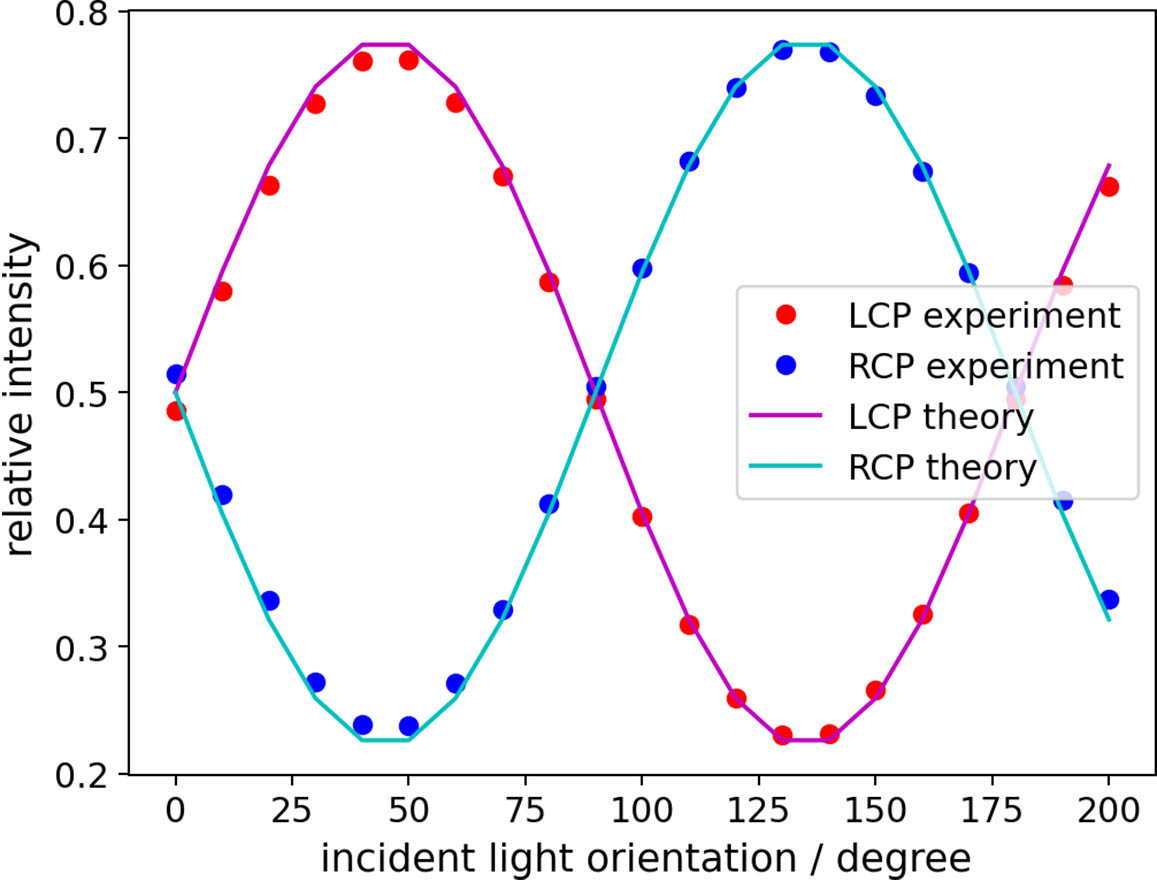
Fig. 7. Measured relative intensity in the PSF lobes (scatter plots) compared to theoretical results (solid lines); LCP data being the photon summation of the upper-right and lower-left lobes, normalized to total number of photons; and RCP data being the photon summation of the other two lobes, normalized to total number of photons.

下载图片 查看所有图片

2.4. Uncertainties in the estimation

Uncertainties arise because of noise when estimating the 3D coordinates x, y, and z of the point emitters and incident light polarization θ. For the spatial coordinates, their theoretically best precision can be described using the Cramer–Rao lower-bound metric proposed by Chao et al.^[24].

X={x,y,z} are parameters to be estimated from the recorded images. Assume a short noise-limited system; the Fisher information matrix Iij can be expressed as Ii,j=∑k=1K1µX,k+β(∂lnµX,k∂Xi)T(∂lnµX,k∂Xj),(7)where µX,k is the expected count of the signal photons of the k-th pixel. It is a combination of LCP and RCP components, each given by the forward PSF model in Section 2.1, with intensity coefficients being cL2 and cR2. β is the expected count of background photons per pixel. K refers to the total number of pixels where the PSF distributes its energy.

The theoretically best precision can be given by the square root of the Cramer–Rao lower bound, which is the inverse of the diagonal elements of the Fisher information matrix; thus, we have σ(Xi)≥Iii−1. Figure 8(a) shows the calculated precision with 8000 signal photons and 10 background photons per pixel, a condition that is achievable in single-molecule experiments. It is observed that the theoretical precision in x, y, and z can maintain better than 20 nm over a depth range of 4 µm.

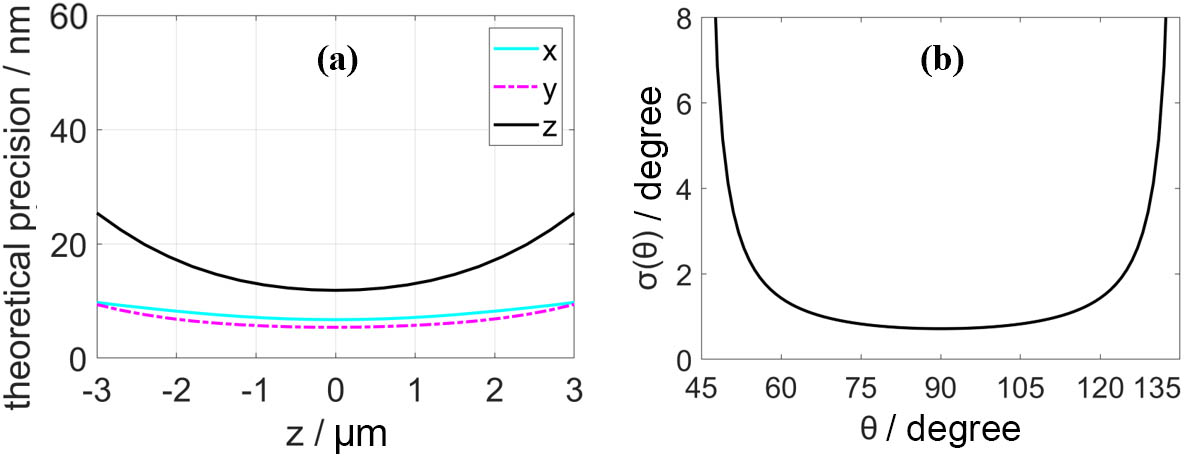
Fig. 8. Estimated uncertainties for (a) spatial coordinates x, y, and z and (b) incident light polarization parameter θ.

下载图片 查看所有图片

For the uncertainties in θ, we calculate from Eq. (6). With N signal photons in total, we have NL=N(cosθ−sinθ)2/2+Kβ/2 photons in the LCP image and NR=N(cosθ+sinθ)2/2+Kβ/2 photons in the RCP image. Taking the difference between the two, we have θ=arcsin[(NR−NL)/N]/2. Using the error propagation theory and under Poisson noise condition [i.e., σ(NL)=NL,σ(NR)=NR], we can write σ(θ)=σ[NL(θ)]2+σ[NR(θ)]2N2−[NL(θ)−NR(θ)]2=NL(θ)+NR(θ)N2−[NL(θ)−NR(θ)]2.(8)

Figure 8(b) shows a plot of σ(θ) with N=8000, Kβ=1000. We can see that theoretical uncertainty is below 4° for θ ∈ [50º, 130º]. The uncertainty increases dramatically at θ = 45º and 135° because at those angles, the LCP or RCP component in the PSF vanishes completely.

3. Conclusion

In this work, we report a geometric-phase-based helical PSF to simultaneously estimate the 3D position and dipole orientation of point emitters. Unlike conventional methods, no polarization splitting is needed; thus, the optical configuration is compact and robust. In addition, it is an achromatic PSF, in contrast to the narrow bandwidth PSFs engineered using a dynamic phase; and it yields higher photon efficiency than using liquid-crystal spatial light modulators. Note that the method is not limited to helical PSF; other PSF designs for 3D localization microscopy also possess the potential to be enhanced for the same purpose.