Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays

Yizhou Qian; Zhiyong Yang; Yu-Hsin Huang; Kuan-Heng Lin; Shin-Tson Wu

doi:doi:10.29026/oes.2022.220021

Opto-Electronic Science, 2022, 1 (12): 220021, Published Online: Jan. 17, 2023

Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays

论文大纲

Yizhou Qian ^*Zhiyong Yang ^*Yu-Hsin Huang ^*Kuan-Heng Lin ^*Shin-Tson Wu ^*

Author Affiliations

College of Optics and Photonics, University of Central Florida, Orlando, FL 32816, USA

nanowire LED microdisplay AR/VR light engines angular color shift

Abstract

The emission wavelength of InGaN/GaN dot-in-wire LED can be tuned by modifying the nanowire diameter, but it causes mismatched angular distributions between blue, green, and red nanowires because of the excitation of different waveguide modes. Besides, the far-field radiation patterns and light extraction efficiency are typically calculated by center dipoles, which fails to provide accurate results. To address these issues, we first compare the simulation results between central dipole and dipole cloud with experimental data. Next, we calculate and analyze the display metrics for full-color nanowire LEDs by 3D dipole cloud. Finally, we achieve unnoticeable angular color shift within ±20° viewing cone for augmented reality (AR) and virtual reality (VR) displays with an improved light extraction efficiency.

1 Introduction

High resolution density, wide field of view (FoV), lightweight and compact formfactor, and low power consumption are demanding requirements for augmented reality (AR) and virtual reality (VR) displays¹. Compared to active-matrix liquid crystal displays (LCDs) and organic light-emitting diode (OLED) displays, microLED (μLED) is attracting more ·attention due to its high peak brightness, excellent dark state, high resolution density, small formfactor, and long lifetime^2-5. Recently, JBD (Jade Bird Display) announced a 0.22-inch full-color μLED panel with 5K pixels per inch (PPI) by monolithic integration, and the red, green, and blue (R, G, B) sub-pixel pitch is only 2.5 μm. At 2022 Touch Taiwan, PlayNitride also exhibited a 0.49-inch full-color µLED demo with 2.5-µm subpixel size by quantum-dot color conversion and sub-pixel rendering. However, to match with human visual acuity which is 60 pixels per degree (PPD), a PPI of 6.7K is required for a 0.3-inch display panel to offer 40° FoV for AR applications⁶. To reduce the pixel size further, the increased sidewall defects would dramatically decrease the internal quantum efficiency (IQE), which in turn increases the power consumption^7-10. In addition, producing efficient GaN based green and red μLEDs remains a technical challenge¹¹.

Nanowire LEDs show great potential for achieving high resolution density and high external quantum efficiency (EQE) at the same time^12-14. In 2018, Aledia reported a nanowire LED¹² whose EQE is independent of pitch size when the pitch size is reduced from 1000 μm to 5 μm. For nanowire LEDs with submicron diameter, the IQE can still achieve 58.5%¹⁵ and the vertical structure functions as a waveguide to effectively couple the light out¹⁶. Additionally, the out-of-plane design can effectively enhance dopant incorporation^{17, 18}, increase heat dissipation¹⁹, reduce dislocation density^{20, 21}, and support multi-color monolithic integration^22-24. Among different nanowire structures, InGaN/GaN dot-in-wire hexagonal LED is attractive due to its diameter-dependent emission wavelength and excellent electrical performance²⁵. Remarkably, the emission wavelength of the InGaN/GaN nanowire LED depends on its diameter due to the shorter lateral diffusion length of Indium adatom than GaN adatom²⁶. In comparison with small diameter nanowires, the large diameter LED exhibits a reduced Indium adatom incorporation and, therefore, a smaller percentage of Indium existing in its active region, which in turn leads to a shorter emission wavelength. Thus, a full-color display can be achieved by solely changing the nanowire’s diameter. However, these sub-wavelength nanowires exhibit different angular radiation patterns in the far-field, leading to a noticeable angular color shift²⁷. Additionally, the size-dependent waveguide modes are excited in each nanowire so that each one has a different outcoupling efficiency to the environment²⁸. For AR/VR applications, a directional light engine is preferred due to the small etendue of human eye pupil^{29, 30} whose accepting cone is typically within ±20°. Therefore, the geometry of the nanowire should be optimized to achieve matched radiation patterns for the three primary colors, high light extraction efficiency (LEE), and narrow angular luminance distribution simultaneously.

In this paper, we optimize the InGaN/GaN nanowire LED geometry by 3D dipole cloud through a commercial wave optics simulation software Finite-Difference Time-Domain (FDTD, Ansys inc.). Firstly, we match the InP nanowire’s angular distribution results from 2D dipole cloud simulation with measurement and compare it with traditional central dipole simulation method to validate the accuracy of the model. Secondly, we calculate and analyze the radiation pattern, color gamut, angular color shift, and LEE of full-color InGaN/GaN nanowire LEDs by 3D dipole cloud. Finally, we optimize the nanowire LED by geometrical engineering. After optimization, the angular color shift within the ±20° viewing cone is consistently lower than the human eye’s just-noticeable difference, and the angular full width at half maximum (FWHM) of [blue, green, red] nanowire LEDs is reduced from [48°, 47°, 35°] to [37°, 33°, 24°], while the effective LEE of RGB nanowire LEDs is increased by 7.8%, 36.2%, and 7.4%, respectively.

2 Results and discussion

2.1 Angular distribution matching of InP nanowire LED

Figure 1(a) shows the 3D FDTD simulation regime and the structure of cylindrical InP nanowire LEDs³¹. The main body of nanowires is immersed with resin and the top electrode is a transparent indium tin oxide (ITO) film. The FDTD simulation regime is defined by 16 layers of steep-angle perfect matched layer (SA-PML). Detailed simulation parameters are included in Table S1 (Supplementary information). The diameter of the nanowire is 230 nm with 2-μm height which includes a 1.2-μm p-InP layer. The active layer is composed of single layer dipole cloud corresponding to the single quantum well layer. The thickness of resin and top ITO layer is 1.7 μm and 200 nm, respectively. The top of the nanowire is covered with a thin spherical capping of ITO. The dispersion of both InP and ITO is considered^{32, 33}. Due to circular symmetry, three dipoles oscillating along x-, y-, z-direction are simulated separately with a 50-nm spacing along x-direction. Figure 1(b) shows the normalized polar plot comparison of spectrally integrated electroluminescence (EL) between simulated and experimental data from ref.³¹. The calculation of spectrally and spatially integrated angular distribution by FDTD 2D power monitor will be discussed in detail in Section 2D Angular distribution and LEE calculation. The emission wavelength is 805 nm~840 nm, which is dominated by wurtzite portion of InP nanowire. Therefore, the dipole oscillating along c-axis (z-axis) is weaker than that of the other two. The measured data (black curve) indicates that InP nanowire EL exhibits a batwing profile and the peak intensity locates at ~10°, which is totally different from the response calculated by traditional simulation method (blue curve) that only uses a single dipole in the center of the nanowire. On the other hand, a good agreement between the dipole cloud simulation (red curve) and the measured data is found. A clear batwing profile where the peak intensity takes place at 14° is found, and the minor differences result from inhomogeneous boarding by surface defects. The dipole cloud simulation shows a pronounced accuracy due to the following two reasons. First, the central dipole method ignores the dipoles close to the edge of the active layer(s), which causes a significant mismatch due to the neglect of high-order mode excited by symmetry breaking. Second, the dipoles close to edge of the active layer(s) typically have a heavier geometrical weightage. Consequently, dipole cloud simulation is necessary when calculating the performance of nanowire LEDs whose diameter is larger than 200 nm.

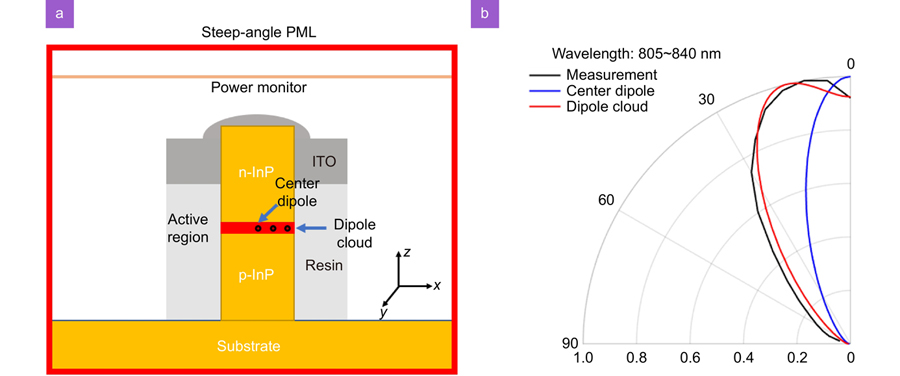
(a) 3D-FDTD InP nanowire LED simulation schematic. (b) Simulated far-field radiation patterns of InP nanowire LED. The experimental data (black curve) included for comparison are from ref.31.

Fig. 1. (a) 3D-FDTD InP nanowire LED simulation schematic. (b) Simulated far-field radiation patterns of InP nanowire LED. The experimental data (black curve) included for comparison are from ref.³¹.

下载图片查看所有图片

2.2 Full-color InGaN/GaN simulation model

Our multicolor single InGaN/GaN dot-in-nanowire LED model is built based on Ra’s experimental results²⁵. As indicated in Fig. 2(a), each nanowire consists of 300-nm n-GaN layer, 60-nm six vertically aligned InGaN/GaN quantum dots layer (active region), 150-nm p-GaN layer, and 150-nm GaN capping layer. The refractive index of the 10-nm Ti mask follows Palik’s handbook³⁴ and the dispersions of GaN and GaN/InGaN active region are calculated by Liu et al³⁵. The nanowire except for the capping is immersed in polyimide whose refractive index is 1.5. The diameter of blue, green, and red nanowires is 630 nm, 420 nm, and 220 nm, respectively. The boundary condition is 16-layer SA-PML to absorb all the escaped light. Hexagonal prism and the capping layer are precisely constructed in the simulation with 10-nm and 5-nm mesh, respectively, along all the x-, y-, and z-directions. Detailed simulation parameters are included in Table S2 (Supplementary information). A large emission box monitor is placed around the structure in the air to calculate the emission power of the LED. The substrate side of the 3D large box monitor is open to get rid of the substrate loss. Small dipole box monitors are placed surrounding each dipole source to calculate the dipole power. Therefore, the light extraction efficiency is calculated by the ratio of the emission power to the dipole power. Besides, the far-field distribution map is captured by the 2D power monitor placed above the structure.

(a) Schematic of FDTD simulation model in x-z plane. (b) Top view of blue hexagonal nanowire LED. (c) Measured EL spectra of single nanowire LEDs with different diameters from ref.25.

Fig. 2. (a) Schematic of FDTD simulation model in x-z plane. (b) Top view of blue hexagonal nanowire LED. (c) Measured EL spectra of single nanowire LEDs with different diameters from ref.²⁵.

下载图片查看所有图片

In x-y plane, due to the hexagonal structure, dipoles are divided into two directions: short axis and long axis, which are defined by inscribed circle and circumscribed circle, respectively. During each simulation, the long axis dipoles are matched with x-axis initially. Then, the short axis dipoles are matched to x-axis by simply rotating the structure by 30°. Here, we denote this axis dependence to be L and S. Each adjacent dipole is separated by 50 nm. For an example of blue nanowire LED shown in Fig. 2(b), the short axis and long axis consist of 6 and 7 dipoles, respectively. For GaN, its crystal structure is wurtzite³⁶; therefore, the dipoles oscillating along c-axis are neglected and only two polarizations of dipoles are simulated: in-axis and out-of-axis. Here, we denote this axis dependency to be I and O. Due to the hexagonal symmetry condition, a total of 804 dipoles are considered in blue nanowire. For green nanowire LEDs, 4 dipoles are simulated along short axis and 5 dipoles are considered for long axis, which results in a total number of 516 dipoles. For red LEDs, the response of 228 dipoles consisting of 2 dipoles for short axis and 3 dipoles for long axis is calculated. The emission wavelength of dipole sources follows the unfiltered measured emission spectra²⁵ (solid lines in Fig. 2(c)). All the three nanowires without color filters have side lobe emission since the Indium adatom diffusion is difficult to be perfectly controlled. In addition, the red nanowire emission spectrum is relatively broad (FWHM~120 nm) since it is formed by InGaN³⁷. After applying color filters, the side lobes are suppressed significantly, which increases the color purity and therefore enlarges the color gamut. Details will be discussed in Section LEE and near-field distribution maps.

2D Angular distribution and LEE calculation

From FDTD 2D power monitor, the far field distribution A as a function of (θ, φ) is calculated for each wavelength λ, polarization state p (I or O), simulation axis a (L or S), and dipole position (x, z). Firstly, the wavelength and polarization dependencies can be eliminated by considering the spectral average of the source³⁸:

$A_{1} (θ, φ, x, z, a) = \frac{\sum_{p = I, O} \int A (θ, φ, x, z, λ, p, a) S (λ) d λ}{2 \int S (λ) d λ},$

where θ is the polar angle, φ is the azimuthal angle, and S(λ) is the emission spectrum. The simulation axis dependence can be eliminated by separating A₁ into long-axis dipoles and short-axis dipoles. In addition, the position independent angular distribution is calculated by integrating the active area in x-y plane and then summing the results together from each active layer. The position-averaged angular distribution for long axis (A_2L) and short axis (A_2S) can be calculated as:

$A_{2 L} (θ, φ) = \frac{\sum_{z = 1}^{6} \int_{0}^{R_{L}} A_{1 L} (θ, φ, x, z) 2 π x d x}{6 π R_{L}^{2}},$

$A_{2 S} (θ, φ) = \frac{\sum_{z = 1}^{6} \int_{0}^{R_{S}} A_{1 S} (θ, φ, x, z) 2 π x d x}{6 π R_{L}^{2}},$

where R_L and R_S represent the radius of long-axis dipoles and short-axis dipoles, respectively. Note that in Eq. (2b), the short axis response should also be normalized by circumscribed circle area for a fair comparison. The total response is the summation of all the dipoles. Here, the angle between long axis and short axis is 30°, and the angle between adjacent long axes is 60°. Therefore, the final angular distribution A₃ can be obtained from the summation of all the short- and long-axis dipole responses:

$A_{3} (θ, φ) = \sum_{k = 0}^{5} A_{2 L} (θ, φ + 60 k) + A_{2 S} (θ, φ + 60 k + 30),$

where k describes the in-plane rotation.

The LEE of an LED is defined by the ratio of the emitting power and dipole power. For each dipole, the LEE can be calculated as:

$η (x, z, λ, p, a) = \frac{P_{E} (x, z, λ, p, a)}{P_{D} (x, z, λ, p, a)},$

where P_E is the total power received by the large emission box monitor and P_D is the total power calculated by the small dipole box monitor as shown in Fig. 2(a). Similar to Eq. (1), the wavelength and polarization state independent LEE can be calculated as:

$η_{1} (x, z, a) = \frac{\sum_{p = I, O} \int η (x, z, λ, p, a) S (λ) d λ}{2 \int S (λ) d λ} .$

The position-averaged angular distributions for long- and short-axis dipole responses are:

$η_{2 L} (θ, φ) = \frac{\sum_{z = 1}^{6} \int_{0}^{R_{L}} η_{1 L} (θ, φ, x, z) 2 π x d x}{6 π R_{L}^{2}},$

$η_{2 S} (θ, φ) = \frac{\sum_{z = 1}^{6} \int_{0}^{R_{S}} η_{1 S} (θ, φ, x, z) 2 π x d x}{6 π R_{S}^{2}} .$

Here, the short-axis dipole response is normalized by the inscribed circle area because each LEE is calculated separately. The total LEE is the summation of both axis dipole responses:

$η_{3} = B_{L} η_{2 L} + B_{S} η_{2 S},$

where B_L= $\frac{2}{2 + \sqrt{3}}$ and B_S= $\frac{\sqrt{3}}{2 + \sqrt{3}}$ are the weightage coefficients for long axis and short axis, respectively.

For AR applications, we define the effective LEE to be the light received within ±20° in the far-field because only the extracted light within this accepting cone can be received by the imaging system. Therefore, the wavelength and polarization state independent effective LEE in Eq. (5) can be expressed as:

$\begin{array}{l} η_{1} (20) (x, z, a) = \\ \frac{\sum_{p = I, O} \int r (x, z, λ, p, a) η (x, z, λ, p, a) S (λ) d λ}{2 \int S (λ) d λ}, \end{array}$

where r is the ±20° spectral coefficient which is calculated as:

$r (x, z, λ, p, a) = \frac{\int_{0}^{20} \int_{0}^{180} A (θ, φ, x, z, λ, p, a) d φ d θ}{\int_{0}^{90} \int_{0}^{180} A (θ, φ, x, z, λ, p, a) d φ d θ} .$

The calculation of the rest part is identical to the total LEE as shown in Eqs. (6–8).

2D Angular distribution and angular color shift

Figure 3(a–c) depict the normalized 2D angular distribution calculated in Section 2D Angular distribution and LEE calculation for blue, green, and red nanowire LEDs, respectively. By summing the results from both long and short axes, the final angular distribution is almost circular symmetric. Among these, the blue nanowire LED (Fig. 3(a)) shows the broadest angular distribution because it has the largest diameter and shortest emission wavelength. Therefore, high-order waveguide modes are excited, which results in a large emission angle from the capping layer. In addition, the peak intensity for green nanowire LED’s angular distribution (Fig. 3(b)) is not located at center. On the other hand, the red nanowire LED (Fig .3(c)) can efficiently concentrate light in the normal direction.

Fig. 3. (a–c) Normalized 2D angular distribution for (a) blue, (b) green, and (c) red LEDs. (d) Normalized 1D angular distribution when azimuthal angle φ=0°.

下载图片查看所有图片

Figure 3(d) depicts the angular distribution of blue, green, and red nanowire LEDs when the azimuthal angle φ=0°. Among these, the angular distribution of green LED shows a batwing profile, and its peak intensity takes place at θ~26°. The FWHM of [blue, green, red] nanowire LEDs is [48°, 47°, 35°], respectively, which are all narrower than Lambertian distribution where the FWHM occurs at 60°. On the other hand, the angular mismatch between RGB nanowire LEDs results in a color shift at different view angles (θ).

Figure 4(a) shows the color gamut of the nanowire LEDs and 18 selected reference colors in Macbeth ColorChecker at 0° viewing angle³⁹. Without applying color filters, the nanowire LED only covers 55.7% DCI-P3 color space and 40.6% Rec.2020. With color filters, the color gamut boosts to 118.5% DCI-P3 and 86.4% Rec.2020. Such a big improvement results from the suppression of side lobe caused by Indium diffusion. Based on 1D angular distribution in Fig. 3(d) and emission spectrum in Fig. 2(c), the angular color shift from 0° to 30° with 1° interval is calculated by our home-made MATLAB code. Figure 4(b) describes the color shift trend for mixing colors because of RGB angular distribution mismatch. As the inset of Fig. 4(b) shows, at ±20° accepting cone, the average color shift is 0.023, which exceeds human eye’s just-noticeable level (∆u'∆v'≤0.02). The issue gets worse as the viewing angle further increases and the average color shift reaches 0.042 at 30° because the RGB color ratio is further increased as shown in Fig. 3(d).

(a) Simulated color triangle of the GaN/InGaN nanowire LED display and CIE coordinates of 18 reference colors at 0° viewing angle. (b) Simulated color shift of 18 reference colors from 0° to 20° viewing angle. Inset: Simulated average color shift from 0° to 30° viewing angle.

Fig. 4. (a) Simulated color triangle of the GaN/InGaN nanowire LED display and CIE coordinates of 18 reference colors at 0° viewing angle. (b) Simulated color shift of 18 reference colors from 0° to 20° viewing angle. Inset: Simulated average color shift from 0° to 30° viewing angle.

下载图片查看所有图片

2.5 LEE and near-field distribution maps

According to Eqs. (5–7), the total LEE of blue, green, and red nanowire LEDs is calculated to be 22%, 49.5%, and 57%. Besides, the LEE of each dipole is highly dependent on its horizontal direction (x-direction) as shown in Fig. S1 (Supplementary information). These results agree well with previous simulation works³⁸. Due to the broad angular distribution, the effective LEE for blue, green, and red nanowires calculated by Eq. (8) is reduced to 9.25%, 18.79%, and 33.02%. Near-field distribution maps of long-axis dipoles at the edge of nanowire in Fig. S2 (Supplementary information) also validate the calculated angular distribution and LEE results.

2.6 Optimization

For such nanowire LEDs, the angular distribution and LEE are highly dependent on three factors: 1) n-GaN/p-GaN thickness, 2) p-GaN capping layer thickness, and 3) nanowire diameter. The n-GaN/p-GaN thickness determines the interference between the dipole in MQW and the reflection from the substrate, air, and Ti mask; the p-GaN capping thickness decides the outcoupling efficiency, and the diameter controls possible waveguide modes in the nanowire. Since the emission wavelength is highly dependent on the diameter, we focus on optimizing the first two factors. Considering the real application that all electrodes are fabricated at the same height, the main bodies of all nanowires (except the capping) are kept at the same height. In other words, n-GaN and p-GaN hexagonal prism (except the capping) change simultaneously, resulting in a varying vertical position of active layers. Thus, the 2-dimensional optimization is performed by sweeping the vertical position of the active layers with a 10-nm step and thickness of p-GaN capping from 0 to 300 nm with a 30-nm step (Fig. 5). Limited by our computer memory, only the long axis dipoles with x- and y-polarization at the edge of the nanowire will be simulated since they obtain the heaviest geometrical weightage. For RGB nanowires having a different diameter, different optimized geometries are calculated based on following criteria: 1) narrower angular FWHM for a higher light directionality, 2) matched radiation pattern for reducing angular color shift, and 3) higher effective LEE.

(a–c) 2D colormap of angular FWHM as a function of n-GaN thickness and p-GaN capping height: (a) blue, (b) green, and (c) red nanowire LEDs. (d–f) 2D colormap of effective LEE as a function of n-GaN thickness and p-GaN capping height: (d) blue, (e) green, and (f) red nanowire LEDs.

Fig. 5. (a–c) 2D colormap of angular FWHM as a function of n-GaN thickness and p-GaN capping height: (a) blue, (b) green, and (c) red nanowire LEDs. (d–f) 2D colormap of effective LEE as a function of n-GaN thickness and p-GaN capping height: (d) blue, (e) green, and (f) red nanowire LEDs.

下载图片查看所有图片

Figure 5(a–c) describes the optimized angular FWHM for each nanowire. The 2D maps indicate that increasing capping height consistently increases the angular FWHM for all the cases because the emission of escaped light is tilted by the capping. In addition, the angular FWHM and the total LEE (Fig. S3, Supplementary information) are both dependent on the n-GaN thickness because excited waveguide modes in the nanowire are very sensitive to its geometrical variation. At a specific n-GaN thickness, the directional radiation mode is constructively interfered with the reflected wave; at the same time, high-order modes could be suppressed by destructive interference. To have a comprehensive understanding on how to improve efficiency, we plot the 2D colormaps of effective LEE based on Eq. (8) as shown in Fig. 5(d–f). Based on these results, we find the optimal conditions for blue, green, and red nanowire LEDs are: 1) removing the p-GaN capping completely, and 2) setting the n-GaN thickness at 120 nm, 240 nm, and 250 nm, respectively.

Based on the optimized geometry, we repeat the simulation of each case by 3D dipole cloud. Compared to the results in Fig. 3(a–c), a significant improvement is found in the optimized angular distribution as Fig. 6(a–c) shows. Especially for green nanowire (Fig. 6(b)), the batwing profile is suppressed. Figure 6(d) indicates that the angular FWHM of [blue, green, red] nanowire LEDs is reduced from [48°, 47°, 35°] to [37°, 33°, 24°], respectively. In contrast to unoptimized data (solid lines), the optimized angular distribution (dashed lines) shows a better match in the 0°–20° range. However, due to the excitation of higher order modes, a shoulder feature atθ=32° is found in blue nanowire LED. As calculated from Eq. (8), the effective LEE of blue, green, and red nanowire LEDs increases from [9.3%, 18.8%, 30.6%] to [10.0%, 25.6%, 33.0%], respectively. The enhancement ratio is 7.4% for blue, 36.2% for green, and 7.8% for red, respectively.

(a–c) Normalized 2D angular distribution for optimized (a) blue, (b) green, and (c) red LEDs. (d) Comparison of normalized 1D angular distribution between unoptimized (solid lines) and optimized (dashed lines) nanowire LEDs.

Fig. 6. (a–c) Normalized 2D angular distribution for optimized (a) blue, (b) green, and (c) red LEDs. (d) Comparison of normalized 1D angular distribution between unoptimized (solid lines) and optimized (dashed lines) nanowire LEDs.

下载图片查看所有图片

If the blue and green InGaN/GaN nanowire LEDs can achieve 58.5% IQE¹⁵ and red nanowire LED can achieve 32.2% IQE⁴⁰, then the corresponding effective EQE for AR applications will be blue = 5.9%, green = 15.0%, and red = 10.6%. For µLEDs, its EQE decreases as the mesa size decreases due to sidewall defects and surface recombination. This dependency can be relieved by the potassium hydroxide (KOH) passivation treatment on the sidewall^{41, 42}, while this method still requires validation for mass production. In comparison with the size-dependent blue^{9, 43} and green InGaN µLED^43-47 and assuming 100% of the produced light can be coupled into the imaging system, our blue nanowire LED shows a better performance than µLED whose mesa size is smaller than 10 µm as shown in Fig. 7(a). In addition, Fig. 7(b) indicates that the effective LEE of green nanowire LEDs is even higher than that of the 80-µm µLED. Compared to AlGaInP red µLEDs⁴⁸, our red nanowire LED is more efficient than that with a 20-µm chip size (Fig. 7(c)). Remarkably, in comparison with the 10-µm mesa size, our blue nanowire LED provides a similar brightness, while green and red nanowire LEDs can offer 1.6× and 1.4× higher efficiency, respectively. Therefore, nanowire LEDs show a pronounced higher efficiency than µLED under small pixel size and high resolution density.

Comparison between calculated effective EQE of nanowire LED (horizontal dash lines) with measured EQE of (a) blue InGaN µLEDs from ref.9,43, (b) green InGaN µLEDs from ref.43-47 and (c) red AlGaInP µLEDs from ref.48 as a function of mesa diameter. Vertical dash lines: EQE of µLEDs with 10-µm mesa size.

Fig. 7. Comparison between calculated effective EQE of nanowire LED (horizontal dash lines) with measured EQE of (a) blue InGaN µLEDs from ref.^9,43, (b) green InGaN µLEDs from ref.^43-47 and (c) red AlGaInP µLEDs from ref.⁴⁸ as a function of mesa diameter. Vertical dash lines: EQE of µLEDs with 10-µm mesa size.

下载图片查看所有图片

In contrast to Fig. 4(b), the angular color shift of 18 reference colors after optimization shown in Fig. 8(a) is reduced, especially for green colors because of the suppressed batwing profile. At 20°, the average color shift is reduced from 0.023 to 0.013 and it is not noticeable until θ > 25° ( Fig. 8(b)), which is already beyond the current acceptance cone for AR headsets.

(a) Simulated angular color shift of 18 reference colors from 0° to 20° after optimization. (b) Simulated average color shift from 0° to 30° viewing angle after optimization.

Fig. 8. (a) Simulated angular color shift of 18 reference colors from 0° to 20° after optimization. (b) Simulated average color shift from 0° to 30° viewing angle after optimization.

下载图片查看所有图片

3 Conclusions

In conclusion, we have optimized full-color InGaN/GaN nanowire LEDs for AR/VR applications by 3D dipole cloud simulation. The simulation method is validated by matching with previous experimental data. By removing the p-GaN capping and modifying the position of active layers, the angular color shift within ±20° viewing cone is suppressed dramatically and the angular FWHM of [blue, green, red] nanowire LEDs is reduced from [48°, 47°, 35°] to [37°, 33°, 24°], respectively, which is favorable for near-eye displays. Meanwhile, the effective LEE of blue, green, and red is enhanced by 7.8%, 36.2%, and 7.4%, respectively.

4 Acknowledgements

The UCF group is grateful for the financial support of a.u.Vista Inc., and En-Lin Hsiang for valuable discussions.

Y. Z. Qian proposed the original idea and led the project. Z. Y. Yang helped to calculate color gamut and angular color shift. S. T. Wu supervised the project and edited the manuscript.

The authors declare no competing financial interests.

Supplementary information for this paper is available at https://doi.org/10.29026/oes.2022.220021

References

[1] Xiong JH, Hsiang EL, He ZQ, Zhan T, Wu STAugmented reality and virtual reality displays: emerging technologies and future perspectivesLight Sci Appl20211021610.1038/s41377-021-00658-8Xiong JH, Hsiang EL, He ZQ, Zhan T, Wu ST. Augmented reality and virtual reality displays: emerging technologies and future perspectives. Light Sci Appl10, 216 (2021).

[2] Huang YG, Hsiang EL, Deng MY, Wu STMini-LED, Micro-LED and OLED displays: present status and future perspectivesLight Sci Appl2020910510.1038/s41377-020-0341-9Huang YG, Hsiang EL, Deng MY, Wu ST. Mini-LED, Micro-LED and OLED displays: present status and future perspectives. Light Sci Appl9, 105 (2020).

[3] Huang YG, Tan GJ, Gou FW, Li MC, Lee SL et alProspects and challenges of mini‐LED and micro‐LED displaysJ Soc Inf Disp20192738740110.1002/jsid.760Huang YG, Tan GJ, Gou FW, Li MC, Lee SL et al. Prospects and challenges of mini‐LED and micro‐LED displays. J Soc Inf Disp27, 387–401 (2019).

[4] Chen Z, Yan SK, Danesh CMicroLED technologies and applications: characteristics, fabrication, progress, and challengesJ Phys D Appl Phys20215412300110.1088/1361-6463/abcfe4Chen Z, Yan SK, Danesh C. MicroLED technologies and applications: characteristics, fabrication, progress, and challenges. J Phys D Appl Phys54, 123001 (2021).

[5] Yang X, Lin Y, Wu TZ, Yan ZJ, Chen Z et alAn overview on the principle of inkjet printing technique and its application in micro-display for augmented/virtual realitiesOpto-Electron Adv2022521012310.29026/oea.2022.210123Yang X, Lin Y, Wu TZ, Yan ZJ, Chen Z et al. An overview on the principle of inkjet printing technique and its application in micro-display for augmented/virtual realities. Opto-Electron Adv5, 210123 (2022).

[6] Tan GJ, Lee YH, Zhan T, Yang JL, Liu S et alFoveated imaging for near-eye displaysOpt Express201826250762508510.1364/OE.26.025076Tan GJ, Lee YH, Zhan T, Yang JL, Liu S et al. Foveated imaging for near-eye displays. Opt Express26, 25076–25085 (2018).

[7] Wu YF, Ma JS, Su P, Zhang LJ, Xia BZFull-color realization of micro-LED displaysNanomaterials202010248210.3390/nano10122482Wu YF, Ma JS, Su P, Zhang LJ, Xia BZ. Full-color realization of micro-LED displays. Nanomaterials10, 2482 (2020).

[8] Han SC, Xu CC, Li HJ, Liu SG, Xu HW et alAlGaInP-based Micro-LED array with enhanced optoelectrical propertiesOpt Mater202111411086010.1016/j.optmat.2021.110860Han SC, Xu CC, Li HJ, Liu SG, Xu HW et al. AlGaInP-based Micro-LED array with enhanced optoelectrical properties. Opt Mater114, 110860 (2021).

[9] Olivier F, Tirano S, Dupré L, Aventurier B, Largeron C et alInfluence of size-reduction on the performances of GaN-based micro-LEDs for display applicationJ Lumin201719111211610.1016/j.jlumin.2016.09.052Olivier F, Tirano S, Dupré L, Aventurier B, Largeron C et al. Influence of size-reduction on the performances of GaN-based micro-LEDs for display application. J Lumin191, 112–116 (2017).

[10] Olivier F, Daami A, Dupré L, Henry F, Aventurier B et al25‐4: investigation and improvement of 10 μm pixel‐pitch GaN‐based micro‐LED arrays with very high brightnessSID Symp Digest Tech Papers20174835335610.1002/sdtp.11615Olivier F, Daami A, Dupré L, Henry F, Aventurier B et al. 25‐4: investigation and improvement of 10 μm pixel‐pitch GaN‐based micro‐LED arrays with very high brightness. SID Symp Digest Tech Papers48, 353–356 (2017).

[11] Bulashevich KA, Kulik AV, Karpov SYOptimal ways of colour mixing for high‐quality white‐light LED sourcesPhys Status Solidi A201521291491910.1002/pssa.201431576Bulashevich KA, Kulik AV, Karpov SY. Optimal ways of colour mixing for high‐quality white‐light LED sources. Phys Status Solidi A212, 914–919 (2015).

[12] Gilet P, Robin IC52-1: invited paper: nanostructures on silicon to solve the active display paradigmsSID Symp Digest Tech Papers20184968468710.1002/sdtp.12349Gilet P, Robin IC. 52-1: invited paper: nanostructures on silicon to solve the active display paradigms. SID Symp Digest Tech Papers49, 684–687 (2018).

[13] Zhao SR, Nguyen HPT, Kibria MG, Mi ZTIII-Nitride nanowire optoelectronicsProg Quantum Electron201544146810.1016/j.pquantelec.2015.11.001Zhao SR, Nguyen HPT, Kibria MG, Mi ZT. III-Nitride nanowire optoelectronics. Prog Quantum Electron44, 14–68 (2015).

[14] Zhou XJ, Tian PF, Sher CW, Wu J, Liu HZ et alGrowth, transfer printing and colour conversion techniques towards full-colour micro-LED displayProg Quantum Electron20207110026310.1016/j.pquantelec.2020.100263Zhou XJ, Tian PF, Sher CW, Wu J, Liu HZ et al. Growth, transfer printing and colour conversion techniques towards full-colour micro-LED display. Prog Quantum Electron71, 100263 (2020).

[15] Jain B, Velpula RT, Bui HQT, Nguyen HD, Lenka TR et alHigh performance electron blocking layer-free InGaN/GaN nanowire white-light-emitting diodesOpt Express20202866567510.1364/OE.28.000665Jain B, Velpula RT, Bui HQT, Nguyen HD, Lenka TR et al. High performance electron blocking layer-free InGaN/GaN nanowire white-light-emitting diodes. Opt Express28, 665–675 (2020).

[16] Yan RX, Gargas D, Yang PFNanowire photonicsNat Photonics2009356957610.1038/nphoton.2009.184Yan RX, Gargas D, Yang PF. Nanowire photonics. Nat Photonics3, 569–576 (2009).

[17] Ra YH, Lee CRCore–shell tunnel junction nanowire white-light-emitting diodeNano Lett2020204162416810.1021/acs.nanolett.0c00420Ra YH, Lee CR. Core–shell tunnel junction nanowire white-light-emitting diode. Nano Lett20, 4162–4168 (2020).

[18] Zhao S, Liu XH, Woo SY, Kang JJ, Botton GA et alAn electrically injected AlGaN nanowire laser operating in the ultraviolet-C bandAppl Phys Lett201510704310110.1063/1.4927602Zhao S, Liu XH, Woo SY, Kang JJ, Botton GA et al. An electrically injected AlGaN nanowire laser operating in the ultraviolet-C band. Appl Phys Lett107, 043101 (2015).

[19] Gong Z, Jin SR, Chen YJ, McKendry J, Massoubre D et alSize-dependent light output, spectral shift, and self-heating of 400 nm InGaN light-emitting diodesJ Appl Phys201010701310310.1063/1.3276156Gong Z, Jin SR, Chen YJ, McKendry J, Massoubre D et al. Size-dependent light output, spectral shift, and self-heating of 400 nm InGaN light-emitting diodes. J Appl Phys107, 013103 (2010).

[20] Ra YH, Kang S, Lee CRUltraviolet light-emitting diode using nonpolar algan core–shell nanowire heterostructuresAdv Opt Mater20186170139110.1002/adom.201701391Ra YH, Kang S, Lee CR. Ultraviolet light-emitting diode using nonpolar algan core–shell nanowire heterostructures. Adv Opt Mater6, 1701391 (2018).

[21] Monemar B, Ohlsson BJ, Gardner NF, Samuelson LNanowire-based visible light emitters, present status and outlookSemicond Semimet201694227271Monemar B, Ohlsson BJ, Gardner NF, Samuelson L. Nanowire-based visible light emitters, present status and outlook. Semicond Semimet94, 227–271 (2016).

[22] Liu XH, Sun Y, Malhotra Y, Wu YP, Mi ZTMonolithic integration of multicolor InGaN LEDs with uniform luminescence emissionOpt Express202129328263283210.1364/OE.435871Liu XH, Sun Y, Malhotra Y, Wu YP, Mi ZT. Monolithic integration of multicolor InGaN LEDs with uniform luminescence emission. Opt Express29, 32826–32832 (2021).

[23] Wang RJ, Nguyen HPT, Connie AT, Lee J, Shih I et alColor-tunable, phosphor-free InGaN nanowire light-emitting diode arrays monolithically integrated on siliconOpt Express201422A1768A177510.1364/OE.22.0A1768Wang RJ, Nguyen HPT, Connie AT, Lee J, Shih I et al. Color-tunable, phosphor-free InGaN nanowire light-emitting diode arrays monolithically integrated on silicon. Opt Express22, A1768–A1775 (2014).

[24] Ito K, Lu WF, Katsuro S, Okuda R, Nakayama N et alIdentification of multi-color emission from coaxial GaInN/GaN multiple-quantum-shell nanowire LEDsNanoscale Adv2022410211010.1039/D1NA00299FIto K, Lu WF, Katsuro S, Okuda R, Nakayama N et al. Identification of multi-color emission from coaxial GaInN/GaN multiple-quantum-shell nanowire LEDs. Nanoscale Adv4, 102–110 (2022).

[25] Ra YH, Wang RJ, Woo SY, Djavid M, Sadaf SM et alFull-color single nanowire pixels for projection displaysNano Lett2016164608461510.1021/acs.nanolett.6b01929Ra YH, Wang RJ, Woo SY, Djavid M, Sadaf SM et al. Full-color single nanowire pixels for projection displays. Nano Lett16, 4608–4615 (2016).

[26] Sekiguchi H, Kishino K, Kikuchi AEmission color control from blue to red with nanocolumn diameter of InGaN/GaN nanocolumn arrays grown on same substrateAppl Phys Lett20109623110410.1063/1.3443734Sekiguchi H, Kishino K, Kikuchi A. Emission color control from blue to red with nanocolumn diameter of InGaN/GaN nanocolumn arrays grown on same substrate. Appl Phys Lett96, 231104 (2010).

[27] Gou FW, Hsiang EL, Tan GJ, Chou PT, Li YL et alAngular color shift of micro-LED displaysOpt Express201927A746A75710.1364/OE.27.00A746Gou FW, Hsiang EL, Tan GJ, Chou PT, Li YL et al. Angular color shift of micro-LED displays. Opt Express27, A746–A757 (2019).

[28] Mangalgiri GM, Manley P, Riedel W, Schmid MDielectric nanorod scattering and its influence on material interfacesSci Rep20177431110.1038/s41598-017-03721-wMangalgiri GM, Manley P, Riedel W, Schmid M. Dielectric nanorod scattering and its influence on material interfaces. Sci Rep7, 4311 (2017).

[29] Zhan T, Hsiang EL, Li K, Wu STEnhancing the optical efficiency of near-eye displays with liquid crystal opticsCrystals20211110710.3390/cryst11020107Zhan T, Hsiang EL, Li K, Wu ST. Enhancing the optical efficiency of near-eye displays with liquid crystal optics. Crystals11, 107 (2021).

[30] Zou JY, Zhan T, Hsiang EL, Du XP, Yu XM et alDoubling the optical efficiency of VR systems with a directional backlight and a diffractive deflection filmOpt Express202129206732068610.1364/OE.430920Zou JY, Zhan T, Hsiang EL, Du XP, Yu XM et al. Doubling the optical efficiency of VR systems with a directional backlight and a diffractive deflection film. Opt Express29, 20673–20686 (2021).

[31] Motohisa J, Kohashi Y, Maeda SFar-field emission patterns of nanowire light-emitting diodesNano Lett2014143653366010.1021/nl501438rMotohisa J, Kohashi Y, Maeda S. Far-field emission patterns of nanowire light-emitting diodes. Nano Lett14, 3653–3660 (2014).

[32] Dinges HW, Burkhard H, Lösch R, Nickel H, Schlapp WRefractive indices of InAlAs and InGaAs/InP from 250 to 1900 nm determined by spectroscopic ellipsometryAppl Surf Sci19925447748110.1016/0169-4332(92)90090-KDinges HW, Burkhard H, Lösch R, Nickel H, Schlapp W. Refractive indices of InAlAs and InGaAs/InP from 250 to 1900 nm determined by spectroscopic ellipsometry. Appl Surf Sci54, 477–481 (1992).

[33] König TAF, Ledin PA, Kerszulis J, Mahmoud MA, El-Sayed MA et alElectrically tunable plasmonic behavior of nanocube–polymer nanomaterials induced by a redox-active electrochromic polymerACS Nano201486182619210.1021/nn501601eKönig TAF, Ledin PA, Kerszulis J, Mahmoud MA, El-Sayed MA et al. Electrically tunable plasmonic behavior of nanocube–polymer nanomaterials induced by a redox-active electrochromic polymer. ACS Nano8, 6182–6192 (2014).

[34] Palik ED. Handbook of Optical Constants of Solids Vol. 3 (Academic Press, San Diego, 1998).

[35] Liu ZY, Wang K, Luo XB, Liu SPrecise optical modeling of blue light-emitting diodes by Monte Carlo ray-tracingOpt Express2010189398941210.1364/OE.18.009398Liu ZY, Wang K, Luo XB, Liu S. Precise optical modeling of blue light-emitting diodes by Monte Carlo ray-tracing. Opt Express18, 9398–9412 (2010).

[36] Krames MR, Shchekin OB, Mueller-Mach R, Mueller GO, Zhou L et alStatus and future of high-power light-emitting diodes for solid-state lightingJ Disp Technol2007316017510.1109/JDT.2007.895339Krames MR, Shchekin OB, Mueller-Mach R, Mueller GO, Zhou L et al. Status and future of high-power light-emitting diodes for solid-state lighting. J Disp Technol3, 160–175 (2007).

[37] Robin Y, Pristovsek M, Amano H, Oehler F, Oliver RA et alWhat is red? On the chromaticity of orange-red InGaN/GaN based LEDsJ Appl Phys201812418310210.1063/1.5047240Robin Y, Pristovsek M, Amano H, Oehler F, Oliver RA et al. What is red? On the chromaticity of orange-red InGaN/GaN based LEDs. J Appl Phys124, 183102 (2018).

[38] Ryu HYEvaluation of light extraction efficiency of GaN-based nanorod light-emitting diodes by averaging over source positions and polarizationsCrystals201882710.3390/cryst8010027Ryu HY. Evaluation of light extraction efficiency of GaN-based nanorod light-emitting diodes by averaging over source positions and polarizations. Crystals8, 27 (2018).

[39] McCamy CS, Marcus H, Davidson JGA color-rendition chartJ Appl Photogr Eng197629599McCamy CS, Marcus H, Davidson JG. A color-rendition chart. J Appl Photogr Eng2, 95–99 (1976).

[40] Nguyen HPT, Zhang SF, Cui K, Korinek A, Botton GA et alHigh-efficiency InGaN/GaN dot-in-a-wire red light-emitting diodesIEEE Photonics Technol Lett20122432132310.1109/LPT.2011.2178091Nguyen HPT, Zhang SF, Cui K, Korinek A, Botton GA et al. High-efficiency InGaN/GaN dot-in-a-wire red light-emitting diodes. IEEE Photonics Technol Lett24, 321–323 (2012).

[41] Wong MS, Lee C, Myers DJ, Hwang D, Kearns JA et alSize-independent peak efficiency of III-nitride micro-light-emitting-diodes using chemical treatment and sidewall passivationAppl Phys Express20191209700410.7567/1882-0786/ab3949Wong MS, Lee C, Myers DJ, Hwang D, Kearns JA et al. Size-independent peak efficiency of III-nitride micro-light-emitting-diodes using chemical treatment and sidewall passivation. Appl Phys Express12, 097004 (2019).

[42] Ley RT, Smith JM, Wong MS, Margalith T, Nakamura S et alRevealing the importance of light extraction efficiency in InGaN/GaN microLEDs via chemical treatment and dielectric passivationAppl Phys Lett202011625110410.1063/5.0011651Ley RT, Smith JM, Wong MS, Margalith T, Nakamura S et al. Revealing the importance of light extraction efficiency in InGaN/GaN microLEDs via chemical treatment and dielectric passivation. Appl Phys Lett116, 251104 (2020).

[43] Smith JM, Ley R, Wong MS, Baek YH, Kang JH et alComparison of size-dependent characteristics of blue and green InGaN microLEDs down to 1 μm in diameterAppl Phys Lett202011607110210.1063/1.5144819Smith JM, Ley R, Wong MS, Baek YH, Kang JH et al. Comparison of size-dependent characteristics of blue and green InGaN microLEDs down to 1 μm in diameter. Appl Phys Lett116, 071102 (2020).

[44] Templier FGaN-based emissive microdisplays: a very promising technology for compact, ultra-high brightness display systemsJ Soc Inf Disp20162466967510.1002/jsid.516Templier F. GaN-based emissive microdisplays: a very promising technology for compact, ultra-high brightness display systems. J Soc Inf Disp24, 669–675 (2016).

[45] Zhanghu M, Hyun BR, Jiang FL, Liu ZJUltra-bright green InGaN micro-LEDs with brightness over 10M nitsOpt Express202230101191012510.1364/OE.451509Zhanghu M, Hyun BR, Jiang FL, Liu ZJ. Ultra-bright green InGaN micro-LEDs with brightness over 10M nits. Opt Express30, 10119–10125 (2022).

[46] Wang L, Wang L, Chen CJ, Chen KC, Hao ZB et alGreen InGaN quantum dots breaking through efficiency and bandwidth bottlenecks of micro-LEDsLaser Photonics Rev202115200040610.1002/lpor.202000406Wang L, Wang L, Chen CJ, Chen KC, Hao ZB et al. Green InGaN quantum dots breaking through efficiency and bandwidth bottlenecks of micro-LEDs. Laser Photonics Rev15, 2000406 (2021).

[47] Hashimoto R, Hwang J, Saito S, Nunoue SHigh‐efficiency green‐yellow light‐emitting diodes grown on sapphire (0001) substratesPhys Status Solidi C2013101529153210.1002/pssc.201300238Hashimoto R, Hwang J, Saito S, Nunoue S. High‐efficiency green‐yellow light‐emitting diodes grown on sapphire (0001) substrates. Phys Status Solidi C10, 1529–1532 (2013).

[48] Fan KL, Tao J, Zhao YZ, Li PY, Sun WC et alSize effects of AlGaInP red vertical micro-LEDs on silicon substrateResults Phys20223610544910.1016/j.rinp.2022.105449Fan KL, Tao J, Zhao YZ, Li PY, Sun WC et al. Size effects of AlGaInP red vertical micro-LEDs on silicon substrate. Results Phys36, 105449 (2022).

1 Introduction

2 Results and discussion

2.1 Angular distribution matching of InP nanowire LED

2.2 Full-color InGaN/GaN simulation model

2D Angular distribution and LEE calculation

2D Angular distribution and angular color shift

2.5 LEE and near-field distribution maps

2.6 Optimization

3 Conclusions

4 Acknowledgements

Yizhou Qian, Zhiyong Yang, Yu-Hsin Huang, Kuan-Heng Lin, Shin-Tson Wu. Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays[J]. Opto-Electronic Science, 2022, 1(12): 220021.

Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays

1 Introduction

2 Results and discussion

2.1 Angular distribution matching of InP nanowire LED

Fig. 1. (a) 3D-FDTD InP nanowire LED simulation schematic. (b) Simulated far-field radiation patterns of InP nanowire LED. The experimental data (black curve) included for comparison are from ref.³¹.

2.2 Full-color InGaN/GaN simulation model

Fig. 2. (a) Schematic of FDTD simulation model in x-z plane. (b) Top view of blue hexagonal nanowire LED. (c) Measured EL spectra of single nanowire LEDs with different diameters from ref.²⁵.

2D Angular distribution and LEE calculation

2D Angular distribution and angular color shift

Fig. 3. (a–c) Normalized 2D angular distribution for (a) blue, (b) green, and (c) red LEDs. (d) Normalized 1D angular distribution when azimuthal angle φ=0°.

Fig. 4. (a) Simulated color triangle of the GaN/InGaN nanowire LED display and CIE coordinates of 18 reference colors at 0° viewing angle. (b) Simulated color shift of 18 reference colors from 0° to 20° viewing angle. Inset: Simulated average color shift from 0° to 30° viewing angle.

2.5 LEE and near-field distribution maps

2.6 Optimization

Fig. 5. (a–c) 2D colormap of angular FWHM as a function of n-GaN thickness and p-GaN capping height: (a) blue, (b) green, and (c) red nanowire LEDs. (d–f) 2D colormap of effective LEE as a function of n-GaN thickness and p-GaN capping height: (d) blue, (e) green, and (f) red nanowire LEDs.

Fig. 6. (a–c) Normalized 2D angular distribution for optimized (a) blue, (b) green, and (c) red LEDs. (d) Comparison of normalized 1D angular distribution between unoptimized (solid lines) and optimized (dashed lines) nanowire LEDs.

Fig. 8. (a) Simulated angular color shift of 18 reference colors from 0° to 20° after optimization. (b) Simulated average color shift from 0° to 30° viewing angle after optimization.

3 Conclusions

4 Acknowledgements

Article Outline

关于本站 Cookie 的使用提示

全站搜索

Directional high-efficiency nanowire LEDs with reduced angular color shift for AR and VR displays

1 Introduction

2 Results and discussion

2.1 Angular distribution matching of InP nanowire LED

Fig. 1. (a) 3D-FDTD InP nanowire LED simulation schematic. (b) Simulated far-field radiation patterns of InP nanowire LED. The experimental data (black curve) included for comparison are from ref.31.

2.2 Full-color InGaN/GaN simulation model

Fig. 2. (a) Schematic of FDTD simulation model in x-z plane. (b) Top view of blue hexagonal nanowire LED. (c) Measured EL spectra of single nanowire LEDs with different diameters from ref.25.

2D Angular distribution and LEE calculation

2D Angular distribution and angular color shift

Fig. 3. (a–c) Normalized 2D angular distribution for (a) blue, (b) green, and (c) red LEDs. (d) Normalized 1D angular distribution when azimuthal angle φ=0°.

Fig. 4. (a) Simulated color triangle of the GaN/InGaN nanowire LED display and CIE coordinates of 18 reference colors at 0° viewing angle. (b) Simulated color shift of 18 reference colors from 0° to 20° viewing angle. Inset: Simulated average color shift from 0° to 30° viewing angle.

2.5 LEE and near-field distribution maps

2.6 Optimization

Fig. 5. (a–c) 2D colormap of angular FWHM as a function of n-GaN thickness and p-GaN capping height: (a) blue, (b) green, and (c) red nanowire LEDs. (d–f) 2D colormap of effective LEE as a function of n-GaN thickness and p-GaN capping height: (d) blue, (e) green, and (f) red nanowire LEDs.

Fig. 6. (a–c) Normalized 2D angular distribution for optimized (a) blue, (b) green, and (c) red LEDs. (d) Comparison of normalized 1D angular distribution between unoptimized (solid lines) and optimized (dashed lines) nanowire LEDs.

Fig. 8. (a) Simulated angular color shift of 18 reference colors from 0° to 20° after optimization. (b) Simulated average color shift from 0° to 30° viewing angle after optimization.

3 Conclusions

4 Acknowledgements

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

Fig. 1. (a) 3D-FDTD InP nanowire LED simulation schematic. (b) Simulated far-field radiation patterns of InP nanowire LED. The experimental data (black curve) included for comparison are from ref.³¹.

Fig. 2. (a) Schematic of FDTD simulation model in x-z plane. (b) Top view of blue hexagonal nanowire LED. (c) Measured EL spectra of single nanowire LEDs with different diameters from ref.²⁵.