1 引　言

非本征型法布里-珀罗干涉（Extrinsic Fabry-Perot Interferometric，EFPI）光纤传感器具有灵敏度高、体积小、抗电磁干扰能力强等优点，在****、医疗、油井监测、电力监测等领域已有成熟应用或良好的应用前景^[1-5]。EFPI传感器的输出信号携带着待测信息，需要对干涉光信号进行解调来计算待测量。解调方法主要分为强度解调、波长解调和相位解调三类^[6-8]。相位解调法中的相位生成载波（Phase Generated Carrier，PGC）解调是一种零差解调法。其特点是在信号频带外引入一个高频载波，将待测信号调制到载波边带，再通过微分-交叉相乘（Differential Cross Multiplication, DCM）、反正切（Atan）等运算处理获得待测信号的相位信息，并将环境等引起的随机相位漂移转为直流偏置进而滤除。PGC算法具有灵敏度高、动态范围大、线性度好等优点，自提出以来一直受到广泛关注^[9-11]。

实现PGC解调法的一个关键点是产生载波，具体分为外调制与内调制两种。外调制方法采用压电陶瓷、电光调制器等器件对输出光进行相位调制，外调制法增大了系统的体积，降低了系统的抗电磁干扰能力。内调制通过调节激光器电流实现对波长（频率）的调制。内调制在原本稳定的光功率上叠加一个纹波，从而会引入伴生调幅问题。此外，载波相位调制深度C与EFPI腔长和激光器调制特性dv/di有关，其中v表示光频率，i表示调制电流。在短腔长、低dv/di情况下，C值难以达到最优值，甚至会导致PGC算法不再适用。在系统结构方面，光路传播、电路传输、数模转换等因素还会引起载波相位延迟。以上3种因素会使PGC算法产生解调的非线性误差与谐波失真，甚至导致解调失败。如何抑制非线性失真是近十年来PGC算法的研究热点。

2011年，施清平等采用3×2耦合器引入双路干涉信号，直接调制光源频率，较好地消除了伴生调幅问题^[12]。2017年，Volkov A V等引入载波三倍频与四倍频计算C值，并通过比例积分控制器将C值稳定在PGC-Atan算法中的最优值2.63 rad^[13]。2020年，HOU C B等在PGC-Atan算法基础上，根据载波相位延迟同步法对载波相位延迟进行计算及补偿^[14]。2022年，胡雨润等采用微分交叉相除等运算得到了一种不受C值限制的PGC算法，将C值范围拓宽至0.5~3.5 rad^[15]。上述研究均取得了较好的效果，但缺乏对多种非线性因素综合影响的修正研究。目前研究中，同时抑制多种非线性因素影响的思路是采用椭圆拟合参数重新构造包含待测相位的信号进行相位提取。2019年，QU ZH Y等采用基于最小二乘法的椭圆拟合算法抑制PGC-Atan算法的非线性失真，在1~3 rad的C值范围内，解调信纳比（Signal to Noise and Distortion，SINAD）最高提升37.56 dB。结合椭圆参数与C相关分量估计C值，进而通过闭环比例积分微分模块快速校准C值^[16]。2020年，HOU CH B等采用基于卡尔曼滤波的椭圆拟合算法，减小了PGC-Atan解调中的相位调制深度变化、光强扰动等非线性因素的影响，实现大信号测量，并将总谐波失真（Total Harmonic Distortion，THD）抑制到−61.22 dB^[17]。2020年，严利平等通过提取PGC正交分量参数，构建卡尔曼滤波状态空间观测模型，对正交分量的幅值与偏置进行修正，进而将非线性误差范围减小到±0.03°，实现纳米级精度的位移测量^[18]。2022年，畅楠琪等在PGC算法中引入基于扩展卡尔曼滤波的椭圆拟合算法，并对校正正交信号所需的椭圆拟合参数进行化简，SINAD较经典PGC-Atan算法提高了17.16 dB^[19]。

EFPI传感器的特点之一是体积小，其腔长较短，一般在10 μm到mm量级。若要采用PGC算法解调EFPI的干涉信号，在激光器调制特性难以满足算法要求等情况下，必须解除腔长与激光器调制特性对最优C值的约束。本文从解除最优C值约束和抑制非线性失真角度出发，提出了一种基于系数补偿的改进型PGC-Atan算法（PGC-Correction Coefficient-Atan，PGC-CC-Atan）与一种基于椭圆拟合的改进型PGC-Atan算法（PGC- Ellipse Fitting Algorithm-Atan，PGC-EF-Atan）。所用的椭圆拟合方法为基于分块矩阵的直接最小二乘法，该算法时间复杂度低，抗噪能力强。仿真结果表明PGC-CC-Atan算法可有效抑制C偏离最优值与载波相位延迟的影响，但受伴生调幅影响较严重，适用于外调制或伴生调幅较小的情况；PGC-EF-Atan算法能同时抑制上述3种非线性因素影响。声压解调实验证实了当C值严重偏离2.63 rad时，PGC-EF-Atan算法解调结果的SINAD较PGC-CC-Atan算法提升了11.602 dB，THD降低了10.951%。该算法解调线性度良好，准确度高，解调结果与参考解调仪的解调结果基本一致。

2 非线性因素对PGC算法的影响

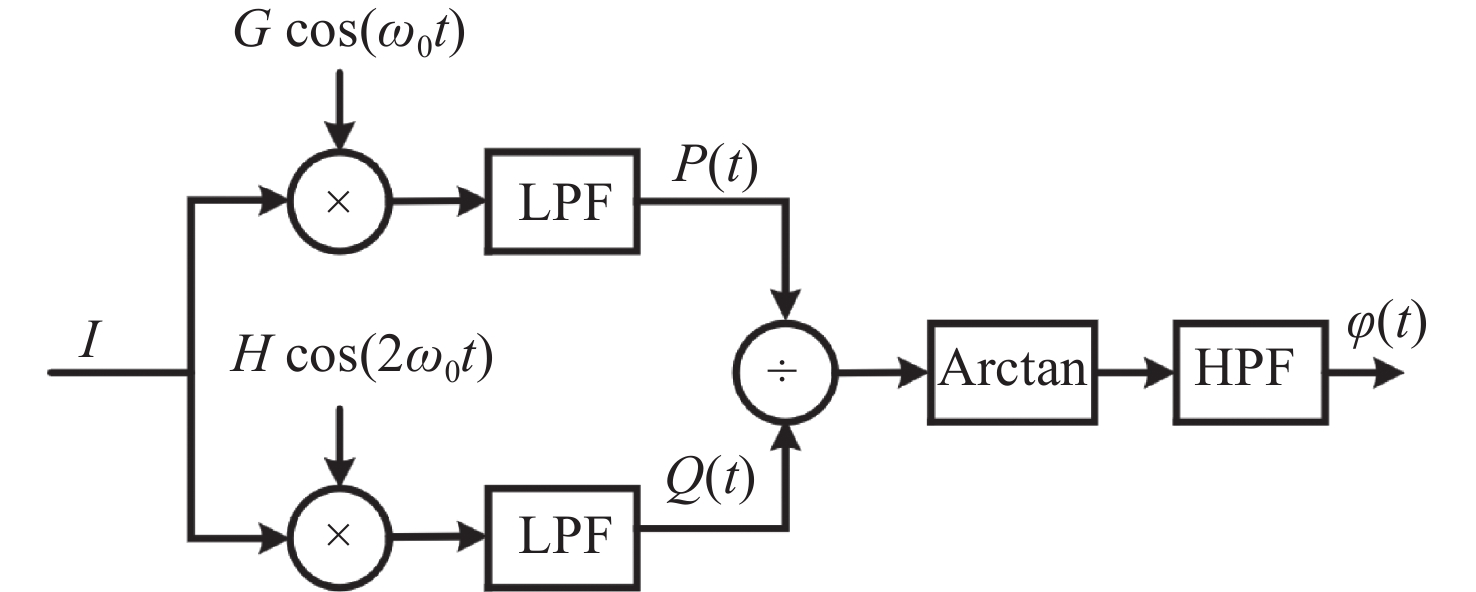
图1为经典PGC-Atan算法的原理图。其中，LPF表示低通滤波器，HPF表示高通滤波器。

图 1. 经典PGC-Atan算法原理图

Fig. 1. Schematic diagram of classical PGC-Atan demodulation

下载图片 查看所有图片

理想情况下，EFPI输出的干涉信号为：

$ I = A + B\cos [C\cos {\omega _0}t + \varphi (t)] \quad, $ (1)

式中，A与B为常数项，与两束相干光光强I₁与I₂有关， A= I₁+I₂，$ B = 2\sqrt {{I_1}{I_2}} $；C为载波相位调制深度；ω₀为载波频率；φ(t)为EFPI传感器受外界影响所产生的相位，包括待测信号、环境干扰和光源调制的固定相位差，可表示为：

$ \varphi (t) = {\varphi _s}(t) + \psi (t) + {\phi _0}(t)\quad, $ (2)

式中，待测信号φ_s(t)=Dcosωt，D为待测信号的幅值，ω为待测信号的频率；ψ(t)为环境影响产生的相位差、初始相位差及其他因素引起的相位差之和；${\phi _0}(t) $为调制产生的固定相位差，可并入ψ(t)。

无非线性因素影响的情况下，干涉信号I经光电转换变为电信号，并与载波一倍频Gcosω₀t、载波二倍频Hcos2ω₀t分别相乘，再经LPF将待测信号中的高次谐波、载波及其边带信号滤除后得到一对信号：

$ P(t) = - BG{J_1}(C)\sin \varphi (t) \quad, $ (3)

$ Q(t) = - BH{J_2}(C)\cos \varphi (t) \quad, $ (4)

式中：G与H分别为载波一倍频与载波二倍频幅值，一般设置相等；J_n(C)为与C值有关的贝塞尔函数项；为便于反正切运算，PGC-Atan算法中的C值一般取最优值2.63 rad，此时满足J₁(C)=J₂(C)，且J₁(C)/J₂(C)变化率最小。P(t)与Q(t)相除并进行反正切运算，再经HPF滤除低频干扰，即可提取待测信号。C的表达式为：

$ C = \frac{{4{\text{π}} nl}}{c}\Delta v \quad,$ (5)

式中：c为光速；n为腔内介质折射率；l为静态腔长；Δv为光频率最大变化量，与调制电流幅值有关。EFPI正常工作时，光程差变化量2nΔl远小于2nl，可认为光程差的变化不会引起C值的明显变化，C值的稳定性主要与调制电流的稳定性有关。调制电流扰动、环境因素、短腔长或激光器调制特性限制均会引起C值扰动或偏离最优C值，从而引起解调幅值失真，甚至解调失败。

光源内调制下，电流调制光频率的同时会引起光功率的变化，使得原本稳定的光功率上叠加一个交变的纹波，产生伴生调幅项(1+mcosω₀t)，其中m为伴生调幅一次谐波的幅度。此外，光路传播、电路传输、数模转换等因素还会引起载波相位延迟θ。受伴生调幅与载波相位延迟影响的干涉信号表达式变为：

$ \begin{split} I =& [1 + m\cos ({\omega _0}t + \theta )] \times \\& {\text{ }}\{ A + B\cos [C\cos ({\omega _0}t + \theta ) + \varphi (t)]\} \quad , \end{split} $ (6)

进而参与反正切运算的一对信号变为：

$ \begin{split} P(t) = &\frac{1}{2}AGm\cos \theta + \frac{1}{2}BGm[{{\rm{J}}_0}(C) - {{\rm{J}}_2}(C)]\;\times\\&\cos \theta \cos \varphi (t) - BG{{\rm{J}}_1}(C)\cos \theta \sin \varphi (t)\quad. \end{split} $ (7)

$ \begin{split} Q(t) =& \frac{1}{2}BHm[{{\rm{J}}_3}(C) - {{\rm{J}}_1}(C)]\cos 2\theta \sin \varphi (t) \; -\\& BH{{\rm{J}}_2}(C)\cos 2\theta \cos \varphi (t) \quad. \end{split} $ (8)

理想情况下P(t)与Q(t)为一对正交信号。但受非线性因素影响，式(7)与式(8)相除后，分子与分母分别包含了cos θ与cos2θ项，以及与m和J_n(C)有关的项，经典PGC-Atan算法无法正确解调待测信号。

3 两种改进型PGC-Atan算法

3.1 PGC-CC-Atan算法

当内调制下m值很小或采用外调制时，即忽略式(7)与式(8)中与m有关的项，P(t)与Q(t)相除得：

$ \frac{{P(t)}}{{Q(t)}} = \frac{{BH{{\rm{J}}_1}(C)\cos \theta }}{{BH{{\rm{J}}_2}(C)\cos 2\theta }}\tan \varphi (t)\quad.$ (9)

对于式(9)，补偿[J₂(C)cos2θ]/[J₁(C)cosθ]即可消除正切函数前与J_n(C)和θ有关的项，使得解调不再受C值约束与载波相位延迟影响。PGC-CC-Atan算法的原理图如图2所示。

图 2. PGC-CC-Atan算法原理图

Fig. 2. Schematic diagram of PGC-CC-Atan demodulation

下载图片 查看所有图片

图2中，C值需要根据式(5)计算得出，前提是已知静态腔长和激光器调制特性dv/di，且调制电流较稳定。θ的提取需要引入载波一倍频正弦信号Gsin ω₀t辅助求解。Gsin ω₀t与干涉信号混乘得：

$ \begin{split} {P_1}(t) = &- \frac{1}{2}AGm\sin \theta - \frac{1}{2}BGm[{{\rm{J}}_0}(C) - {{\rm{J}}_2}(C)]\;\times\\&\sin \theta \cos \varphi (t) + BG{{\rm{J}}_1}(C)\sin \theta \sin \varphi (t) . \end{split} $ (10)

式(10)与式(7)相除并进行反正切再取反即可求得θ。PGC-CC-Atan算法原理简单，但从理论分析来看，载波相位延迟恰为45°和90°时该算法尚存不足。

3.2 PGC-EF-Atan算法

3.2.1 椭圆参数提取与正交信号校正

根据PGC-Atan算法思路，需要一对严格正交的信号进行后续反正切运算。显然，受电流调制度、相位延迟等非线性因素影响的P(t)与Q(t)不再正交，此时，可以重新构建一对包含待测信号信息的正交信号进行解调。整理式(7)和式(8)得：

$ P(t) = a - b\sin [\varphi (t) - {\theta _1}] \text{，} $ (11)

$ Q(t) = - c\cos [\varphi (t) + {\theta _2}] \text{，} $ (12)

式中，

$ \left\{ \begin{gathered} a = \frac{1}{2}AGm\cos \theta \\ b = BG\cos \theta \sqrt {{{\rm{J}}_1}^2(C) + \frac{{{m^2}}}{4}{{[{{\rm{J}}_0}(C) - {{\rm{J}}_2}(C)]}^2}} \\ c = BH\cos 2\theta \sqrt {{{\rm{J}}_2}^2(C) + \frac{{{m^2}}}{4}{{[{{\rm{J}}_3}(C) - {{\rm{J}}_1}(C)]}^2}} \\ {\theta _1} = \arctan \left( - \frac{{m[{{\rm{J}}_0}(C) - {{\rm{J}}_2}(C)]}}{{2{{\rm{J}}_1}(C)}}\right) \\ {\theta _2} = \arctan \left( - \frac{{m[{{\rm{J}}_3}(C) - {{\rm{J}}_1}(C)]}}{{2{{\rm{J}}_2}(C)}}\right) \\ \end{gathered} \right. \quad. $ (13)

式(11)，式(12)的形式更为简单，可以此构建sin[φ(t)+θ₂]与cos[φ(t)+θ₂]作为一对正交信号求解待测信号。根据三角函数sin²[φ(t)+θ₂]+cos²[φ(t)+θ₂] =1，并结合式(11)与式(12)，可得：

$\begin{split} \sin [\varphi (t) + {\theta _2}] =& \quad\frac{1}{{\cos ({\theta _1} + {\theta _2})}} \cdot\\& \left[\frac{{P(t) - a}}{{ - b}} + \frac{{Q(t)}}{{ - c}}\sin ({\theta _1} + {\theta _2})\right] ,\end{split} $ (14)

$ \begin{split} \tan [\varphi (t) + {\theta _2}] =\dfrac{{\dfrac{{[P(t) - a]c}}{b} + Q(t)\sin ({\theta _1} + {\theta _2})}}{{Q(t)\cos ({\theta _1} + {\theta _2})}}, \end{split}$ (15)

$ \begin{split} &\frac{1}{{{b^2}{{\cos }^2}({\theta _1} + {\theta _2})}}{P^2}(t) + \frac{{2\sin ({\theta _1} + {\theta _2})}}{{bc{{\cos }^2}({\theta _1} + {\theta _2})}}P(t)Q(t) \;+ \\&\qquad\frac{1}{{{c^2}{{\cos }^2}({\theta _1} + {\theta _2})}}{Q^2}(t) - \frac{{2a}}{{{b^2}{{\cos }^2}({\theta _1} + {\theta _2})}}P(t) \;- \\&\qquad\frac{{2a\sin ({\theta _1} + {\theta _2})}}{{bc{{\cos }^2}({\theta _1} + {\theta _2})}}Q(t) + \frac{{{a^2}}}{{{b^2}{{\cos }^2}({\theta _1} + {\theta _2})}} = 1 \end{split} \quad. $ (16)

式(15)即为反正切运算的目标，但受非线性因素影响，a、b、c、θ₁和θ₂未知，需进行求解。观察式(16)可发现其结构形如二次曲线的一般方程：

$ e{x^2} + Exy + F{y^2} + Lx + My + N = 0 \quad, $ (17)

式中，(x，y)为二次曲线图像坐标，e、E、F、L、M、N为二次曲线参数。二次曲线参数可任意缩放，令e=1，并将式(16)中P²(t)项的系数归一化，可得：

$ \left\{ \begin{gathered} E = \frac{{2b\sin ({\theta _1} + {\theta _2})}}{c} \\ F = \frac{{{b^2}}}{{{c^2}}} \\ L = - 2a \\ M = - \frac{{2ab\sin ({\theta _1} + {\theta _2})}}{c} \\ N = {a^2} - {b^2}{\cos ^2}({\theta _1} + {\theta _2}) \\ \end{gathered} \right. \quad. $ (18)

根据式(18)可知，E²/4−F=(b/c)²×[sin(θ₁+θ₂)−1] ≤0，可判定以P(t)和Q(t)离散采样点为坐标构建的二次曲线为椭圆或圆。对离散采样点进行椭圆拟合即可得到椭圆参数。椭圆参数与式(15)中未知量a，b/c，sin(θ₁+θ₂)和cos(θ₁+θ₂)之间的关系如下：

$ \left\{ \begin{gathered} a = - \frac{L}{2} \\ b/c = \sqrt F \\ \sin ({\theta _1} + {\theta _2}) = \frac{E}{{2\sqrt F }} \\ \cos ({\theta _1} + {\theta _2}) = \sqrt {1 - \frac{{{E^2}}}{{4F}}} \\ \end{gathered} \right. \quad. $ (19)

将式(19)带入反正切运算式(15)可知，只需求解3个椭圆参数E、F和L即可计算出tan[φ(t)+ θ₂]：

$ \tan [\varphi (t) + {\theta _2}] = \dfrac{{\left[P(t) + \dfrac{L}{2}\right]\Bigg/\sqrt F + Q(t)\dfrac{E}{{2\sqrt F }}}}{{Q(t)\sqrt {1 - {E^2}/(4F)} }} \quad.$ (20)

式(20)中的分子与分母是一对严格正交的信号，经反正切与高通滤波解调出φ(t)，避免了非线性因素的影响。PGC-EF-Atan算法原理图如图3所示。

图 3. PGC-EF-Atan算法原理图

Fig. 3. Schematic diagram of PGC-EF-Atan demodulation

下载图片 查看所有图片

3.2.2 基于分块矩阵的直接最小二乘法拟合椭圆

椭圆拟合方法有多种，如最小二乘法、最小平方中值法、卡尔曼滤波法等。考虑到算法的时间与空间复杂度，本文采用基于分块矩阵的直接最小二乘法拟合椭圆^[20-21]。该算法无需迭代，时间复杂度低，抗噪声能力强，稳定性好，且拟合出的一定是椭圆，并确保有唯一最优解。下面介绍该算法。

令e=[e，E，F，L，M，N]^T，x=[x²，xy，y²，x，y，1]^T，对于椭圆隐式方程有：

$ F(e,x) ={\boldsymbol{ e}} \cdot {\boldsymbol{x}} = e{x^2} + Exy + F{y^2} + Lx + My + N = 0 \quad.$ (21)

F(e，x_i)表示点(x_i，y_i)到二次曲线F(e，x)的代数距离。当约束代数距离平方之和最小时，就是最佳拟合。最小代数距离平方之和||Ve||²_min可表示为：

$ ||{\boldsymbol{Ve}}|{|^2}_{{\rm{min}}} = {\text{min}}\sum\limits_{i = 1}^n {F{{({x_i},{y_i})}^2}} = \min \sum\limits_{i = 1}^n {{{({x_i} \cdot e)}^2}}\quad,$ (22)

式中，V为n×6矩阵，V=[x₁，x₂，……x_n]^T。为了避免平凡解，比如零向量，以及求解e的任意倍数所表示的相同二次曲线，需要对椭圆的参数施加一些限定。一般认为，二次曲线表示椭圆时，有E²−4eF<0，但根据库恩-塔克条件，这个不等式约束条件下不一定有解。由于e可以任意缩放参数，那么令约束条件为4eF−E²=1。构造6×6矩阵U来表示这个约束条件，即e^TUe=1，具体如下：

$ {{\boldsymbol{e}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} 0&0&2&0&0&0 \\ 0&{ - 1}&0&0&0&0 \\ 2&0&0&0&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \\ 0&0&0&0&0&0 \end{array}} \right]{\boldsymbol{e}} = 1 \quad. $ (23)

综上，椭圆拟合的两个约束条件为：||Ve||²_min和e^TUe=1。对||Ve||²_min进行微分，并引入拉格朗日因子λ，可得到如下联立方程：

$ \left\{ \begin{gathered} 2{{\boldsymbol{V}}^{\rm{T}}}{\boldsymbol{Ve}} - 2\lambda {\boldsymbol{Ue}} = 0 \\ {{\boldsymbol{e}}^{\rm{T}}}{\boldsymbol{Ue}} = 1 \\ \end{gathered} \right. \quad, $ (24)

式中，第一个等式可能有多达6组实解，但增加了第二个等式作为约束条件，就可得到第一个等式唯一的正特征值，恰好对应着e^TUe=1的最优解。构造S=V^TV，则有S=λU，进而可得：

$ ||{\boldsymbol{Ve}}|{|^2} = {{\boldsymbol{e}}^{\rm{T}}}{{\boldsymbol{V}}^{\rm{T}}}{\boldsymbol{Ve}} = {{\boldsymbol{e}}^{\rm{T}}}{\boldsymbol{Se}} = \lambda {{\boldsymbol{e}}^{\rm{T}}}{\boldsymbol{Ue}} = \lambda \quad. $ (25)

然而，构造的矩阵U和S是奇异矩阵，求解得到的特征值很可能无穷大或者是复数。此外，在理想情况下，当所有的数据点恰好位于一个椭圆上时，特征值为零。为避免产生非最优或完全错误的解，对矩阵V、U、S、e进行分块。

令V=[V₁V₂]，其中，$ {{\boldsymbol{V}}_1} = \left[ {\begin{array}{*{20}{c}} {{x_1}^2}&{{x_1}{y_1}}&{{y_1}^2} \\ {{x_2}^2}&{{x_2}{y_2}}&{{y_1}^2} \\ \vdots & \vdots & \vdots \\ {{x_n}^2}&{{x_n}{y_n}}&{{y_1}^2} \end{array}} \right] $，$ {{\boldsymbol{V}}_2} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}&1 \\ {{x_2}}&{{y_2}}&1 \\ \vdots & \vdots & \vdots \\ {{x_n}}&{{y_n}}&1 \end{array}} \right] $。

令$ {\boldsymbol{S }}= \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_1}}&{{{\boldsymbol{S}}_2}} \\ {{{\boldsymbol{S}}_2}^{\mathrm{T}}}&{{{\boldsymbol{S}}_3}} \end{array}} \right] $，其中，S₁=V₁^TV₁，S₂= V₁^TV₂，S₃= V₂^TV₂。

令$ {\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_1}}&0 \\ 0&0 \end{array}} \right] $，其中，$ {{\boldsymbol{U}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&2 \\ 0&{ - 1}&0 \\ 2&0&0 \end{array}} \right] $。

令$ {\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_1}} \\ {{{\boldsymbol{e}}_2}} \end{array}} \right] $，其中e₁=(e；E；F)，e₂=(L；M；N)。

因此约束条件变为

$ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_1}}&{{{\boldsymbol{S}}_2}} \\ {{{\boldsymbol{S}}_2}^{\mathrm{T}}}&{{{\boldsymbol{S}}_3}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_1}} \\ {{{\boldsymbol{e}}_2}} \end{array}} \right] = \lambda \cdot \left[ {\begin{array}{*{20}{c}} {{U_1}}&0 \\ 0&0 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_1}} \\ {{{\boldsymbol{e}}_2}} \end{array}} \right] . $ (26)

展开式(26)，求解特征向量与特征值进而可得到椭圆的拟合参数。

4 仿真验证与实验测量

4.1 仿真验证

为验证改进型算法的正确性，在LabVIEW平台搭建经典PGC-Atan算法、PGC-CC-Atan算法、PGC-EF-Atan算法的数值仿真程序。

数值仿真时，为了避免频谱混叠问题，待测信号频率ω、载波频率ω₀及低通滤波器过渡带宽ω_L之间应满足：

$ {\omega _0} - (k{{ - }}1)\omega \gt (k{-}1)\omega + {\omega _{\mathrm{L}}} \quad， $ (27)

式中k表示待测信号的谐波级次。根据PGC运算过程中的贝塞尔函数展开，待测信号的k次谐频分量的幅值正比于J_k(D)。当|J_k(D)|<0.1时，待测信号的k次及以上谐频分量可忽略，待测信号频谱集中在(k−1)ω范围内。

根据上述要求，仿真中给定待测信号的幅值为1 rad，频率为1 600 Hz，载波频率为40 kHz，采样率为1 MHz，所用低通滤波器为椭圆滤波器，通带截止频率为4 kHz，阻带截止频率为6 kHz，通带衰减系数为0.1dB，阻带衰减系数为80 dB，滤波器阶数为8。考虑到实际解调过程中可能遇到的非线性影响因素，数值仿真中设置了相位调制深度偏离2.63 rad、载波相位延迟、伴生调幅这三类问题。

为探究两种改进算法适用的C值范围，仿真中令C值从0.1 rad以0.1 rad步进到6.1 rad，载波相位延迟与电流调制度m均设定为0，经典PGC-Atan算法与两种改进型PGC-Atan算法对待测信号解调的仿真结果如图4（彩图见期刊电子版）所示。

图 4. C值从0.1 rad变化到6.1 rad时3种算法的仿真结果与J₁(C)/J₂(C)的变化趋势

Fig. 4. Simulation results of the three algorithms and the variation trend of J₁(C)/J₂(C) when C deviates from 0.1 rad to 6.1 rad

下载图片 查看所有图片

根据图4可知，仅C值变化时，3种解调算法的解调结果的变化趋势与J₁(C)/J₂(C)有关。其中，经典PGC-Atan算法仅在使得J₁(C)/J₂(C)=1的C值附近能较准确解调，如2.63 rad、6.08 rad。两种改进型算法在一定C值范围内能有效解调，如0.5~3.5 rad、4.1~4.9 rad。但受J₁(C)/J₂(C)=0或±∞影响，当C值在0 rad、3.83 rad、5.1 rad等值附近时，两种改进型算法的解调结果不再准确。

在C值适用范围内选取C=1 rad，载波相位延迟θ从0°变化到80°。电流调制度m设为0，即无伴生调幅影响。经典PGC-Atan算法与两种改进型PGC-Atan算法对待测信号解调的仿真结果如图5所示。

图 5. 两种非线性因素影响下3种算法的仿真结果

Fig. 5. Simulation results of the three algorithms under the influence of the two nonlinear factors

下载图片 查看所有图片

根据图5的仿真结果，两种改进型的解调算法在C值偏离最优值时， 均能有效消除载波相位延迟的影响。进一步，将载波相位延迟θ设定为30°，对不同C值和m值影响下的两种改进型算法进行仿真，结果如图6和图7（彩图见期刊电子版）所示。

图 6. 3种非线性因素影响下PGC-CC-Atan算法仿真结果

Fig. 6. Simulation results of PGC-CC-Atan algorithm under the influence of the three nonlinear factors

下载图片 查看所有图片

图 7. 3种非线性因素影响下PGC-EF-Atan算法仿真结果

Fig. 7. Simulation results of PGC-EF-Atan algorithm under the influence of the three nonlinear factors

下载图片 查看所有图片

由图6仿真结果可知，m值会限制PGC-CC-Atan算法的C值适用范围。当m≤0.1时，各C值下的PGC-CC-Atan算法解调结果基本一致。当m>0.1时，PGC-CC-Atan算法对伴生调幅的抵抗能力与C值有关，C值越大，m对解调结果的影响越小。在C值较大时，尽管仿真结果的幅值随m值（0≤m≤1）变化不明显，但SINAD持续降低。因此，严格来看，只有当外调制或者伴生调幅影响较小甚至可忽略的情况下，PGC-CC-Atan算法才能稳定解调。

由图7仿真结果知，PGC-EF-Atan算法能较好地消除3种非线性因素的影响。当C≥1 rad时，在0~1范围内m取任意值，该算法的解调幅值与SINAD均基本稳定。解调幅值与待测值1 rad之间存在约0.05 rad的误差，这可能与滤波及椭圆拟合的准确度有关。但在C=0.5 rad且m>0.7的情况下，该算法的解调幅值不再准确，SINAD降低。因此，在伴生调幅较严重的情况下，采用PGC-EF-Atan算法解调时的调制深度不应过小。

4.2 实验测量

为验证两种改进型PGC-Atan解调算法的有效性，搭建了如图8所示的解调实验平台。

图 8. EFPI解调实验平台

Fig. 8. EFPI demodulation experiment platform

下载图片 查看所有图片

解调实验采用的EFPI传感器的共振频率为1600 Hz，腔长为335 μm。采用内调制PGC-Atan算法进行解调时，根据式(5)知，若要产生足够的相位调制深度，则需要较大的光频率偏移量。在一定范围内，激光器的光波长（光频率）与驱动电流呈正比，调节正弦调制电流幅值可调节光频率的变化量。然而，较大的正弦调制电流伴随有较大的光功率的变化，易引起严重的伴生调幅问题，且可能超出激光器驱动电流的限制。EFPI解调常用的光源发生器包括分布式反馈（Distributed Feedback，DFB）激光器等。通常DFB激光器的调制特性约为0.01 nm/mA与0.08 mW/mA。对于本实验所用的EFPI，若要调制DFB激光器产生2.63 rad的相位调制深度，则正弦调制电流幅值需达155.6 mA，远超DFB激光器的调制上限。本实验中光源采用垂直腔面发射激光器（Vertical-Cavity Surface-Emitting Laser,VCSEL），其中心波长为1550 nm，调制特性为0.4 nm/mA与0.2 mW/mA，驱动电流上限为25 mA，正弦调制电流峰值为3.84 mA时即可实现2.63 rad的调制深度。

实验中，调制VCSEL的载波由1号信号发生器产生，频率为40 kHz。2号信号发生器产生的1600 Hz正弦信号经电压放大器驱动压电陶瓷声源，向EFPI施加激励。数字式A加权声级计与EFPI并排放置，以标定EFPI探头处的声压。该声级计型号为GM1532，可测声频率上限为8 kHz。EFPI的输出信号经光纤环形器送入光电探测器并转换为电信号。该信号被PICO 4225A采集卡以1 Ms/s的采样速率传入计算机中，并在LabVIEW软件平台进行解调。

4.3 实验结果

4.3.1 C值适用范围实测分析

保持EFPI处的声压一定，调节1号信号发生器，将C值依次设定为0.5 rad、1 rad、1.5 rad、2 rad、2.5 rad和3 rad，采用两种改进型算法对EFPI的腔长变化量进行解调。同时，为了测试改进型算法的解调准确度，采用基于电荷耦合器件（Charge Coupled Device，CCD）的参考解调仪标定EFPI的腔长变化量。测试结果如图9所示。

图 9. 不同C值下两种改进型算法解调结果与参考解调仪结果对比

Fig. 9. Comparison between the demodulation results of the two algorithms under different C and the calibration results of the reference demodulator

下载图片 查看所有图片

从图9可知，PGC-EF-Atan算法在不同C值下均有稳定的解调效果。在本文所用的常规腔长EFPI和光源调制特性限制下，PGC-CC-Atan算法在C=1 rad和C≥2 rad情况下的解调结果与参考解调仪的解调结果相近。这是因为实验中对光源进行内调制时不可避免地会产生伴生调幅问题。在设定实验参数时，可以通过调节激光器的正弦驱动电流幅值改变C值，但随之产生的伴生调幅项中的电流调制深度m值未知。当C=0.5 rad时，PGC-CC-Atan算法的解调结果低于参考结果，结合图6分析，推测此情况下m值已超过0.1。当C=1 rad和C≥2 rad时，伴生调幅项中m值处于PGC-CC-Atan算法解调幅值尚受伴生调幅影响不明显的范围。为确保两种算法有效解调，并降低伴生调幅，后续实验将C值设定为1 rad。

4.3.2 解调能力对比

将C值设定为1 rad，解调实验平台采集到的原始信号波形图与频谱图如图10所示。将采集到的信号分别采用经典PGC-Atan算法、PGC-CC-Atan算法、PGC-EF-Atan算法进行解调，解调结果分别如图11-13所示。3种算法的性能对比如表1所示。图13(c)中校正后的李萨茹图由式(20)的分子与分母作为P(t)与Q(t)绘制所得。

图 10. 原始信号（a）波形图与（b）频谱图

Fig. 10. (a) The waveform and (b) spectrum of the original signal

下载图片 查看所有图片

图 12. PGC-CC-Atan算法解调结果。(a)波形图；(b)频谱图

Fig. 12. Demodulation results using PGC-CC-Atan algorithm. (a) Waveform; (b) spectrum

下载图片 查看所有图片

由图10(b)可知，原始信号的频谱成分主要是待测信号及其各次谐波、载波各倍频信号及其边带信号，未发生频谱混叠。对比图11、图12与图13可知，经典PGC-Atan算法和PGC-CC-Atan算法的解调波形存在失真，且频谱中存在相对强的高次谐波分量谱线。PGC-EF-Atan算法解调结果中，波形失真与高次谐波分量均得到了抑制，且参与反正切运算的一对信号的李萨如图经椭圆拟合算法由椭圆校正为正圆，即这对非正交信号被校正为正交信号。由表1中的SINAD与THD可知，PGC-EF-Atan算法能有效抵抗相位调制深度偏离最优值、载波相位延迟和伴生调幅的影响。

图 11. 经典PGC-Atan算法解调结果。(a)波形图；(b)频谱图

Fig. 11. Demodulation results using PGC-Atan algorithm. (a) Waveform; (b) spectrum

下载图片 查看所有图片

图 13. PGC-EF-Atan算法解调结果。(a)波形图；(b)频谱图；(c)P(t)与Q(t)形成的李萨如图

Fig. 13. Demodulation results of PGC-EF-Atan algorithm. (a) Waveform; (b) spectrum; (c) Lissajous figure of P(t) and Q(t)

下载图片 查看所有图片

4.3.3 PGC-EF-Atan算法解调线性度测试

在C为1 rad条件下，调节2号信号发生器的输出电压，改变声源声压，对PGC-EF-Atan算法解调线性度进行测试，并计算腔长变化量。同时采用参考解调仪标定EFPI的腔长变化量，与PGC-EF-Atan算法解调结果进行对比。为避免EFPI在较大声压下长期工作发生机械劳损，测试过程中EFPI探头处的声压级为42.8~58.1 dB，即探头处声压在2.76~16.07 mPa范围。PGC-EF-Atan算法解调结果与参考解调仪测试结果对比如图14所示。

图 14. PGC-EF-Atan算法解调结果与参考解调仪标定结果对比

Fig. 14. Comparison between the demodulation results of PGC-EF-Atan algorithm and the calibration results of the reference demodulator

下载图片 查看所有图片

根据图14可知，PGC-EF-Atan算法解调结果的线性拟合度r²=0.98200，表明该算法解调线性度良好。该算法拟合得到的EFPI的声压响应灵敏度为13.39664 nm/mPa，与参考解调仪解调结果接近，证实了PGC-EF-Atan算法解调结果准确可信。

5 结　论

本文针对C偏离最优值、伴生调幅、载波相位延迟等非线性因素影响下EFPI传感器的PGC解调，提出了PGC-CC-Atan算法和PGC-EF-Atan算法，旨在将PGC算法用于常规腔长的EFPI解调，消除最优C值对解调的约束，并抑制伴生调幅、载波相位延迟等非线性因素的影响。本文首先介绍了非线性因素影响下的PGC-Atan算法关键步骤的数学形式，然后研究了消除非线性因素影响的方法：PGC-CC-Atan算法通过构造与C和θ相关的系数，直接消去反正切运算式中的非线性影响因素，结构简单；PGC-EF-Atan算法通过基于分块矩阵的最小二乘法拟合椭圆并提取3个椭圆拟合参数，重构了一对包含待测信号的正交信号。最后给出了经典PGC-Atan算法与两种改进型PGC算法的仿真与实验对比。

仿真结果表明，本文提出的PGC-CC-Atan算法和PGC-EF-Atan算法理论上在0.5 rad≤C≤3.5 rad情况下可有效解调。但PGC-CC-Atan算法受m值影响，适用于外调制或伴生调幅很小的内调制。PGC-EF-Atan算法在伴生调幅较大的情况下，C值不宜过小。实验结果表明，在本实验硬件系统条件下，PGC-EF-Atan算法可有效消除非线性因素的影响，有效解调。PGC-CC-Atan算法无法解决伴生调幅问题。PGC-EF-Atan算法的解调信纳比相对PGC-CC-Atan算法提高了11.602 dB，总谐波失真降低了10.951%，且解调线性度良好，准确度高，稳定可靠。