0 引　言

随着光学制造技术的广泛发展，光学检测技术也广泛发展起来。高精度光学元件及系统在航空、极紫外光刻等领域的应用，使得光学检测技术面临了前所未有的挑战。干涉测量作为高精度的检测手段，广泛应用于各种光学元件及系统的测试，尤其是随着相移干涉技术的发明，精度高、速度快成为干涉技术的代名词^[1-2]。最开始的相移干涉技术是定步长的，虽然精度较高，但是对干涉仪硬件和周围环境要求太高，相位计算精度取决于相移精度。随机相移算法能够解除对相移精度的限制，对其进行研究具有重要的意义。

随机相移算法可以分为迭代算法和非迭代算法，也可以分为两步算法和多步算法。由于相移干涉图的光强表达式中未知数较多，一般情况下想要求解相位至少需要三幅干涉图，因此发展了许多多步随机相移算法，其中有两种算法比较经典，一种是2004年Wang等人提出的基于最小二乘法的先进迭代算法（AIA），它解决了帧-帧之间迭代和像素-像素之间迭代的分离的限制，极大地提高了精度^[3]。另一种是2011-2017年，Vargas等人提出的一系列基于主成分分析法（PCA）的相移算法，它将一组可能相关的变量转换为一组不相关的变量值，该算法是非迭代算法，计算速度快^[4-6]。多步算法虽然精度高，但是图像采集时间及计算时间长，不适合光学加工过程中的在线检测。

为了减少图像采集时间及计算时间，发展了很多经典的两步随机相移算法。2012年，Vargas等人提出了格兰-施密特正交化法（GS），该算法不需要相移估计，速度快且易于运行^[7]。2014年，Luo提出采用菱形对角线向量的正交性计算相位和相移的方法（DDV）^[8]。2015年，Niu提出一种计算相移干涉图内积的商从而计算相移的算法（QIP）^[9]。2018年，Cheng提出通过求解四次多项式方程得到相移的方法（QPE）^[10]。因为QIP和QPE计算的是相移值的余弦，因此相移范围被限制在[0,π]之间。2019年，Cheng又提出了通过搜索调制幅度的最小变化系数从而求得相移的方法（CVM）^[11]。上面的算法有一个共同的特点，它们在计算相位之前需要采用滤波算法将背景光强滤掉。然而，滤波算法除了滤除背景光强，还可能引入滤波误差，会影响相位计算精度。

为了避免上述情况，很多非滤波的两步随机相移算法发展起来，也可以分为两大类别，一种是李萨如椭圆拟合法。1992年，Farrell采用了李萨如椭圆拟合法（LEF）计算了待测相位^[12]。2019年，笔者将GS、PCA和LEF进行了结合，精度较前面的滤波两步随机相移算法有较大提升，但是LEF花费的时间相对较长^[13-14]。另一种是最小二乘法。2019年，笔者将干涉图的和差欧式矩阵范数（EMNSD）计算出来的相位作为初值，采用快速最小二乘法（FLSA）计算出来精确的相位，花费时间较少^[15]。2018年，笔者还将LEF和最小二乘法组合成了一种新的算法，LEF计算出来的相位作为初值，采用最小二乘法计算出了更精确的相位^[16]。虽然LEF和最小二乘法都能够实现高精度的相位计算，但是花费时间较多，对光学在线检测不利，因此设计一个没有滤波的、简便的、快速的、高精度的两步随机相移算法迫在眉睫。

针对上述要求，文中设计了一个基于PCA和VU分解法的两步随机相移算法，采用两步PCA计算出来的相位作为迭代初值，扩展干涉图，构造扩展干涉图矩阵，采用VU分解、迭代计算出精确的相位。无论PCA还是VU分解都是简单的矩阵运算，花费时间较少，而且没有滤波的干涉图参与到VU分解运算当中，极大地提升了相位计算精度，该算法易于操作，花费时间少，精度高，在高精度光学在线检测领域将有广泛的应用前景。

1 基本原理

1.1 两步PCA

一般的PCA需要三幅以上相移值等间隔分布于[0,2π]的干涉图，对于两幅相移干涉图，无法通过减去多幅干涉图的平均值去除背景光强求出主成分，从而求出待测相位。针对两幅相移干涉图，设计了一种两步PCA。

两幅相移干涉图的光强表达式可以写成：

$ \begin{split} {I_{i,1}} &= {a_i} + {b_i}\cos \left( {{\varphi _i} + {\delta _1}} \right)= \\ & {a_i} + {b_i}\cos {\varphi _i}\cos {\delta _1} - {b_i}\sin {\varphi _i}\sin {\delta _1} \end{split} $ (1)

$ \begin{split} {I_{i,2}} &= {a_i} + {b_i}\cos \left( {{\varphi _i} + {\delta _2}} \right)= \\ &{a_i} + {b_i}\cos {\varphi _i}\cos {\delta _2} - {b_i}\sin {\varphi _i}\sin {\delta _2} \end{split} $ (2)

式中：$ {a_i} $为背景光强；$ {b_i} $为调制幅度；$ {\varphi _i} $为待测相位；$ {\delta _1} $和$ {\delta _2} $为两幅干涉图的相移值；$ i $为像素序号，$i = 1,2, \cdots ,M$，$ M $为干涉图的像素总数。

采用高通滤波器去除背景光强，并且令${\delta }_{1}\text{=} 0， {\delta }_{2}\text{=}\delta$简化光强表达式，滤波后的干涉图光强表达式为：

$ {\tilde I_{i,1}} = {b_i}\cos {\varphi _i} $ (3)

$ {\tilde I_{i,2}} = {b_i}\cos {\varphi _i}\cos \delta - {b_i}\sin {\varphi _i}\sin \delta $ (4)

采用滤波后的两幅干涉图构造矩阵$ Q $：

$ Q{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{\tilde I}_{1,1}}}&{{{\tilde I}_{2,1}}} \\ {{{\tilde I}_{1,2}}}&{{{\tilde I}_{2,2}}} \end{array}\;\;\;\;\begin{array}{*{20}{c}} \cdots &{{{\tilde I}_{M,1}}} \\ \cdots &{{{\tilde I}_{M,2}}} \end{array}} \right] $ (5)

两个滤波干涉图光强值的协方差矩阵为：

$ C = Q{Q^{\rm{T}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 1}^M {{{\tilde I}^2}_{i,1}} }&{\displaystyle\sum\limits_{i = 1}^M {{{\tilde I}_{i,1}} \cdot {{\tilde I}_{i,2}}} } \\ {\displaystyle\sum\limits_{i = 1}^M {{{\tilde I}_{i,1}} \cdot {{\tilde I}_{i,2}}} }&{\displaystyle\sum\limits_{i = 1}^M {{{\tilde I}^2}_{i,2}} } \end{array}} \right] $ (6)

将协方差矩阵对角化，得到：

$ D = HC{H^{\rm{T}}} $ (7)

式中：$ H{\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&0 \\ {-{{{C_{1,2}}} \mathord{\left/ {\vphantom {{{C_{1,2}}} {{C_{1,1}}}}} \right. } {{C_{1,1}}}}}&1 \end{array}} \right] $。

主成分可以利用公式（8）计算：

$ \begin{split} y &= HQ = \left[ {\begin{array}{*{20}{c}} 1&0 \\ { - {{{C_{1,2}}} \mathord{\left/ {\vphantom {{{C_{1,2}}} {{C_{1,1}}}}} \right. } {{C_{1,1}}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde I}_{i,1}}} \\ {{{\tilde I}_{i,2}}} \end{array}} \right] = \\ & \left[ {\begin{array}{*{20}{c}} {{{\tilde I}_{i,1}}} \\ {{{\tilde I}_{i,2}} - {{{C_{1,2}}} \mathord{\left/ {\vphantom {{{C_{1,2}}} {{C_{1,1}}{{\tilde I}_{i,1}}}}} \right. } {{C_{1,1}}{{\tilde I}_{i,1}}}}} \end{array}} \right] \end{split} $ (8)

$ {{{C_{1,2}}} \mathord{\left/ {\vphantom {{{C_{1,2}}} {{C_{1,1}}}}} \right. } {{C_{1,1}}}} $可以通过公式（9）计算：

$ {{{C_{1,2}}} \mathord{\left/ {\vphantom {{{C_{1,2}}} {{C_{1,1}}{\text{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}\cos \delta } }}{{\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}} }}}}} \right. } {{C_{1,1}}{\text{ = }}\frac{{\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}\cos \delta } }}{{\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}} }}}} = \cos \delta $ (9)

将公式（9）代入公式（8）得到：

$ {y_{i,1}} = {b_i}\cos {\varphi _i} $ (10)

$ {y_{i,2}} = - {b_i}\sin {\varphi _i}\sin \delta $ (11)

为了最终求得待测相位，对公式（10）和公式（11）进行归一化：

$ {\tilde y_{i,1}} = {{{{\tilde y}_{i,1}}} \mathord{\left/ {\vphantom {{{{\tilde y}_{i,1}}} {\left\| {{y_1}} \right\|}}} \right. } {\left\| {{y_1}} \right\|}} = \frac{{{b_i}\cos {\varphi _i}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}} } }} $ (12)

$ {\tilde y_{i,2}} = {{{{\tilde y}_{i,2}}} \mathord{\left/ {\vphantom {{{{\tilde y}_{i,2}}} {\left\| {{y_2}} \right\|}}} \right. } {\left\| {{y_2}} \right\|}} = \frac{{{b_i}\sin {\varphi _i}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\sin }^2}{\varphi _i}} } }} $ (13)

当干涉图中的条纹数量大于1，意味着相位分布超过一个相位周期，因此有如下近似：

$\begin{split} &\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}} -\displaystyle\sum\limits_{i = 1}^M {{b^2}_i{{\sin }^2}{\varphi _i}} = \\ &\quad \displaystyle\sum\limits_{i = 1}^M {{b^2}_i\cos 2{\varphi _i}} \approx 0 \end{split} $ (14)

然后，

$ \sum\limits_{i = 1}^M {{b^2}_i{{\sin }^2}{\varphi _i}} \approx \sum\limits_{i = 1}^M {{b^2}_i{{\cos }^2}{\varphi _i}} $ (15)

最终，待测相位通过反正切函数计算出来。

$ {\varphi _i} = {\arctan ^{ - 1}}\left( {{{{{\tilde y}_{i,2}}} \mathord{\left/ {\vphantom {{{{\tilde y}_{i,2}}} {{{\tilde y}_{i,1}}}}} \right. } {{{\tilde y}_{i,1}}}}} \right) $ (16)

1.2 VU分解法

上面的两步PCA非常简便，可以很快得到待测相位值，但是滤波带来的误差会影响待测相位的计算精度，因此下面以两步PCA计算的相位作为迭代初始相位值，设计无须滤波的VU分解法进一步提高相位求解精度。

笔者将两幅相移干涉图的光强用一个表达式来表示：

$\begin{split} {I_{i,j}} &= {a_i} + {b_i}\cos \left( {{\varphi _i} + {\delta _j}} \right)= \\ & {a_i} + {b_i}\cos {\varphi _i}\cos {\delta _j} - {b_i}\sin {\varphi _i}\sin {\delta _j} \end{split} $ (17)

式中：$ j $为干涉图序号，$j=1,2,\cdots ,N$,$ N $为干涉图的总数，文中$ N{\text{ = }}2 $。

采用两幅干涉图的光强构造一个矩阵：

$ I = {{V}}{{{U}}^{\rm{T}}} = \left( {\begin{array}{*{20}{c}} {{a}}&{{c}}&{ - {{s}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{{1}}^{\rm{T}}}} \\ {{{{u}}^{\rm{T}}}} \\ {{{{v}}^{\rm{T}}}} \end{array}} \right) $ (18)

式中：${{V}} = \left( {\begin{array}{*{20}{c}} {{a}}&{{c}}&{ - {{s}}} \end{array}} \right)$；${{U}} = \left( {\begin{array}{*{20}{c}} {{1}}&{{u}}&{{v}} \end{array}} \right)$；$ {{a}} = \left\{ {{a_i}} \right\} $； $ {{c}} = \left\{ {{b_i}\cos {\varphi _i}} \right\} $；$ {{s}} = \left\{ {{b_i}\sin {\varphi _i}} \right\} $； $ {{u}}{\text{ = }}\left\{ {\cos {\delta _j}} \right\} $；$ {{v}}{\text{ = }}\left\{ {\sin {\delta _j}} \right\} $。

假如已知相移值$ {\delta _j} $，可以通过下式求出矩阵$ V $，从而求出待测相位：

$ V = IU{\left( {{U^{\rm{T}}}U} \right)^{ - 1}} $ (19)

然而，$ {U^{\rm{T}}}U $只有当$ N \geqslant 3 $时才可逆，$ N{\text{ = 2}} $时有奇异矩阵，因此两幅干涉图无法进行VU分解，下面采用扩展干涉图的方法克服矩阵的奇异性。

$ \begin{split} &{G_{i,1}} = {a_{i,1}} \\ &{G_{i,2}} = {a_{i,2}} \\ &{G_{i,3}} = {a_{i,1}} + {b_i}\cos {\varphi _i}\cos {\delta _1} - {b_i}\sin {\varphi _i}\sin {\delta _1} \\ &{G_{i,4}} = {a_{i,2}} + {b_i}\cos {\varphi _i}\cos {\delta _2} - {b_i}\sin {\varphi _i}\sin {\delta _2} \end{split} $ (20)

式中：$ {G_{i,1}} $和$ {G_{i,2}} $来自于采集的两幅干涉图光强$ {G_{i,3}} $和$ {G_{i,4}} $。具体地来说，就是将采集到的两幅干涉图进行低通滤波，得到两幅干涉图的背景光强，作为$ {G_{i,1}} $和$ {G_{i,2}} $，由滤波得到的背景光强和两幅干涉图光强共同构成矩阵$ G $，下面将矩阵进行重写：

$ G{{ = V}}{{{U}}^{\rm{T}}} = \left( {{{{a}}_1}}\quad{{{{a}}_2}}\quad{{c}}\quad{ - {{s}}} \right)\left( {\begin{array}{*{20}{c}} 1&0&1&0 \\ 0&1&0&1 \\ 0&0&{\cos {\delta _1}}&{\cos {\delta _2}} \\ 0&0&{\sin {\delta _1}}&{\sin {\delta _2}} \end{array}} \right) $ (21)

式中：${{V}} = \left( {\begin{array}{*{20}{c}} {{{{a}}_1}}\;\;{{{{a}}_2}}\;\;{{c}}\;\;{ - {{s}}} \end{array}} \right)$；${{U}} = \left( {\begin{array}{*{20}{c}} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & {\cos {\delta _1}} & {\sin {\delta _1}} \\ 0 & 1 & {\cos {\delta _2}} & {\sin {\delta _2}} \end{array}} \right)$；$ {{{a}}_1} = \left\{ {{a_{i,1}}} \right\} $；$ {{{a}}_2} = \left\{ {{a_{i,2}}} \right\} $；$ {{c}} = \left\{ {{b_i}\cos {\varphi _i}} \right\} $；$ s = \left\{ {{b_i}\sin {\varphi _i}} \right\} $。

注意上面的讨论中，假设两幅干涉图的背景光强不同，$ {a_{i,1}} \ne {a_{i,2}} $，在实际实验中，对于不同的干涉图和不同的像素，背景光强都是不同的，如此设计算法可以提高相位计算精度。而在VU分解法中，设计调制幅度$ {b_i} $只和像素位置有关，与干涉图序号无关，主要是方便相位计算。另外，$ {b_i} $既可以放在矩阵$ V $中，也可以放在矩阵$ U $中，所在位置并不影响VU分解。

经过干涉图扩展后，$ {U^{\rm{T}}}U $不再是奇异矩阵，能够求解逆矩阵。

假设已知矩阵$ U $，通过矩阵运算可以求出矩阵$ V $：

$ V = GU{B^{ - 1}} $ (22)

式中：$ B = {U^{\rm{T}}}U $。

同理，如果已知矩阵$ V $，也可以很容易计算出来矩阵$ U $：

$ {U^{\rm{T}}} = {A^{ - 1}}{V^{\rm{T}}}G $ (23)

式中：$ A = {V^{\rm{T}}}V $。

下面介绍一下VU分解法求解相位的具体流程：

1）先采用低通滤波法求出两幅干涉图的背景光强，然后构造矩阵$ G $；

2）利用两步PCA计算出来的相位值作为迭代初值，得到初始化矩阵$ {V_0} $；

3）求出矩阵$ {A_0} = {V_0}^{\rm{T}}{V_0} $，然后求出$ {U_0}^{\rm{T}} = {A_0}^{ - 1}{V_0}^{\rm{T}}G $；

4）利用$ {U_0} $求出$ {B_0} = {U_0}^{\rm{T}}{U_0} $，然后求出$ {V_1} = G{U_0}{B_0}^{ - 1} $；

5）根据$ {V_1} $求出第一次迭代的相位值$ {\tilde \varphi _1}{\text{ = }} {\arctan ^{ - 1}}\left( { - {V_{1(:,4)}}/{V_{1(:,3)}}} \right) $；

6）令$ {V_{1(:,3)}}{\text{ = }}\cos {\tilde \varphi _1} $，${V_{1(:,4)}}{\text{ = }}-\sin \left( {{{\tilde \varphi }_1}} \right)$，更新矩阵$ {V_1} $；

7）依次类推，不断迭代，$ {A_{k - 1}} = {V_{k - 1}}^{\rm{T}}{V_{k - 1}} $，$ {U_{k - 1}}^{\rm{T}} = {A_{k - 1}}^{ - 1}{V_{k - 1}}^{\rm{T}}G $，$ {B_{k - 1}} = {U_{k - 1}}^{\rm{T}}{U_{k - 1}} $，$ {V_k} = G{U_{k - 1}}{B_{k - 1}}^{ - 1} $，直到满足收敛条件$ {E_k} = \sqrt {{{\displaystyle\sum\limits_{i = 1}^M {{{\left( {{{\tilde \phi }_{i,k}} - {{\tilde \phi }_{i,k - 1}}} \right)}^2}} } \mathord{\left/ {\vphantom {\displaystyle{\sum\limits_{i = 1}^M {{{\left( {{{\tilde \phi }_{i,k}} - {{\tilde \phi }_{i,k - 1}}} \right)}^2}} } M}} \right. } M}} < \xi $，求出最终相位为$ {\tilde \varphi _k}{\text{ = }}{\arctan ^{ - 1}}\left( { - {V_{k(:,4)}}/{V_{k(:,3)}}} \right) $。$ k $为迭代次数，$ k=1,2,\cdots $。

在步骤4）中，调制幅度$ {b_i} $将存在于矩阵$ V $中，而在步骤6）中，当完成矩阵$ V $更新后，调制幅度$ {b_i} $将存在于矩阵$ U $中，随着迭代过程的进行，$ {b_i} $在矩阵$ V $和$ U $中轮换，正是由于矩阵$ V $的不断更新和$ {b_i} $在矩阵$ V $和$ U $中的不断轮换，迭代才能向正确方向收敛。

2 模　拟

选择了两步随机相移算法中性能良好的GS^[14]、CVM^[18]及EMNSD&FLSA^[22]与文中求取迭代初值的两步PCA(PCA2)及设计的基于主成分分析和VU分解法的两步相移算法（PCA&VU）进行对比，文中将模拟对比不同类型条纹、不同信噪比的噪声、不同相移值、不同条纹数量等对不同算法的影响，并对比各种算法的计算时间，文中计算机的CPU为Intel(R) Core(TM) i5-8265 U，内存为8 GB。

首先，模拟了圆条纹和不规则条纹干涉图，相位表达式分别为$ \varphi = 5{\text{π }}\left( {{x^2} + {y^2}} \right) $和$ \varphi = 4{\textit{π}} \left( {{x^2}{\text{ + }}{y^2} + {x^3} + {y^3}} \right) +$$4\left[ \begin{array}{l}3{\left( {1 - x} \right)^2}{{\rm{e}}^{ - {x^2} - {{\left( {y + 1} \right)}^2}}} - 10\left( {\dfrac{1}{5}x - {x^3} - {y^5}} \right){{\rm{e}}^{ - {x^2} - {y^2}}}\\ - \dfrac{1}{3}{{\rm{e}}^{ - {{\left( {x + 1} \right)}^2} - {y^2}}}\end{array} \right]$，理论相位分布图如图1(a)和(b)所示。实际情况中，无论是背景光强还是调制幅度都随着干涉图序号和像素序号变化，为了使得模拟更接近于实际情况，设计两幅干涉图的背景光强表达式为${a_i}\left( {x,y} \right) = {R_a}\exp \left[ { - 0.02\left( {{x^2} + {y^2}} \right)} \right]$，调制幅度表达式为$ {b_i}\left( {x,y} \right) = {R_b}\exp \left[ { - 0.02\left( {{x^2} + {y^2}} \right)} \right] $，其中两幅干涉图的$ {R_a} $分别为1和0.95，两幅干涉图的$ {R_b} $分别为0.95和0.9。在干涉图中加入信噪比为20 dB的噪声，两幅相移干涉图相移值设为1 rad，干涉图像素数为401 pixel×401 pixel，圆条纹和不规则条纹干涉图如图1(c)和(d)所示。文中GS、CVM和PCA2采用高斯高通滤波去除背景光强，去除背景光强的干涉图如图1(e)和(f)所示，由此可以看出，滤波仅仅去除了背景光强，并没有去除噪声。

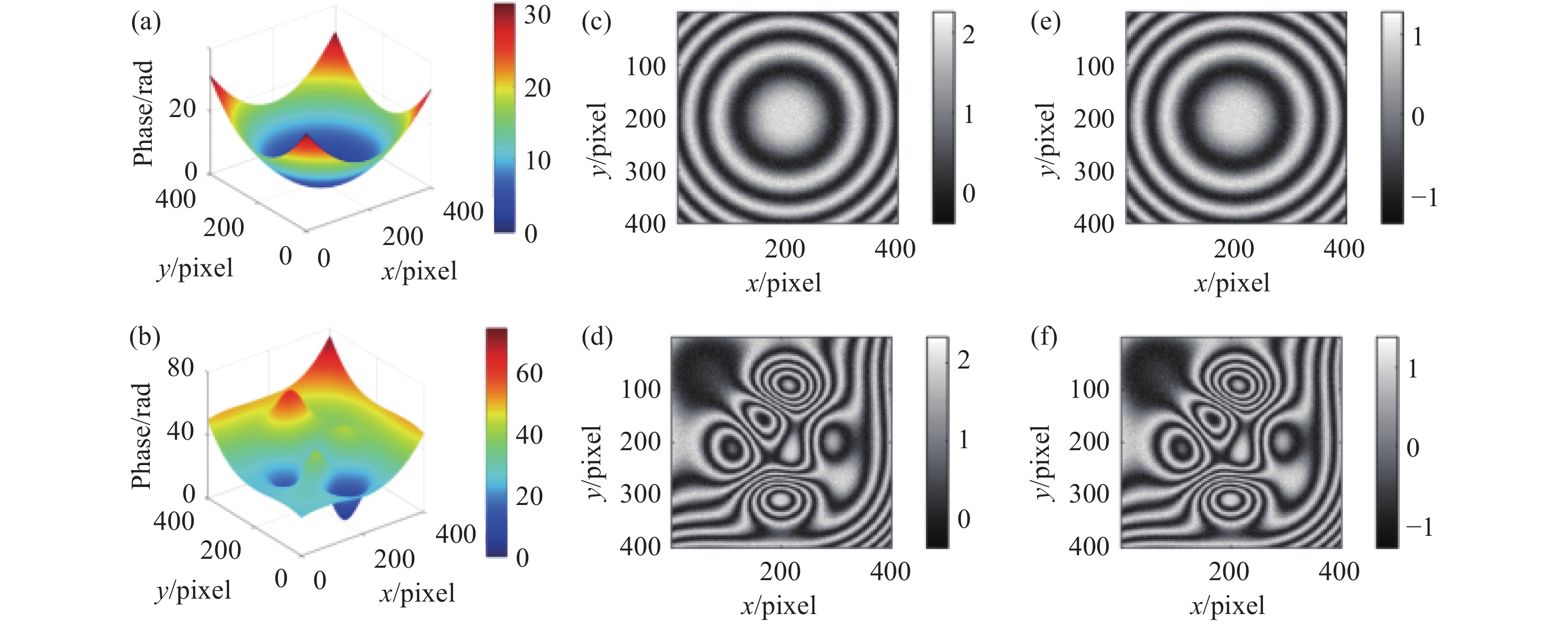
图 1. 模拟相位分布图、干涉图和高斯高通滤波后干涉图。 (a)、(b)圆条纹和不规则条纹对应的理论相位分布图；(c)、(d)圆条纹和不规则条纹干涉图；(e)、(f)高斯高通滤波后的圆条纹和不规则条纹干涉图

Fig. 1. Simulated phase distributions, interferograms and interferograms after Gaussian high-pass filtering. (a), (b) Theoretical phase distributions corresponding to the circular and complex fringes; (c), (d) Interferograms with circular and complex fringes; (e), (f) Interferograms with circular and complex fringes after Gaussian high-pass filtering

下载图片 查看所有图片

采用GS、CVM、EMNSD&FLSA及PCA2和文中设计的PCA&VU计算的圆条纹和不规则条纹的相位误差图如图2所示。图3采用柱形图比较了不同相移算法的相位误差RMS值。可以看出，对于圆条纹和不规则条纹，结论是一样的。GS和PCA2精度一致。CVM算法精度是五种算法中精度最低的，因为背景光强、调制幅度误差及噪声都会影响相移值的寻找。EMNSD&FLSA和PCA&VU精度比较高，主要有两个原因：一是两种算法都没有采用滤波算法去除背景光强。虽然PCA&VU利用滤波的干涉图计算出来的相位作为迭代初值，但是最终相位是利用VU分解法采用没有滤波的干涉图直接计算出来的；另一个原因是两种算法都是迭代算法。虽然EMNSD&FLSA和PCA&VU都是迭代算法，但是也有精度高低之分，文中设计的PCA&VU算法精度比EMNSD&FLSA更高，因为VU分解法考虑了两幅相移干涉图的背景光强不一致问题。

除了算法的精度，计算时间也是考查算法性能的重要因素之一。笔者对五种算法的计算时间在表1中进行了对比，可以看出GS和PCA2花费的时间最少，因为这两种算法没有迭代，算法简便。而CVM虽然没迭代，但是搜索相移值的过程花费时间较多，因此花费的时间最多。EMNSD&FLSA虽然是迭代算法，但由于选取部分数据点进行迭代计算，花费的时间也不算过多。PCA&VU中PCA花费时间较少，VU分解法的迭代计算花费了相对较多的时间，总时间虽然比GS和PCA2多，但是还不足EMNSD&FLSA一半时间，作为一个精度较高的迭代算法，401 pixel×401 pixel花费的时间还不足0.05 s，可以作为高精度的在线检测算法。

图 2. 不同相移算法的相位误差分布图。(a)~(e)圆条纹的相位误差分布图；(f)~(j)不规则条纹的相位误差分布图

Fig. 2. Phase error distributions of different phase-shifting algorithms. (a)-(e) Phase error distributions of circular fringes; (f)-(j) Phase error distributions of irregular fringes

下载图片 查看所有图片

图 3. 针对不同类型条纹，不同相移算法的相位误差RMS值 (20 dB)

Fig. 3. Phase errors RMS of different phase-shifting algorithms with different types of fringes (20 dB)

下载图片 查看所有图片

前面对五种算法的对比主要考虑了不理想的背景光强、调制幅度及噪声等因素，确切地说考查的是不同算法对不理想的背景光强、调制幅度及噪声的敏感程度或抑制能力。为了单纯地判断五种算法自身的精度，采用理想的背景光强、调制幅度模拟了两幅圆条纹和不规则条纹相移干涉图，并且没有在干涉图中加入噪声，最终相位误差RMS值对比结果如图4所示。可以看出，EMNSD&FLSA和PCA&VU没有相位误差，而GS、CVM和PCA2对应的相位误差RMS值虽然远小于非理想情况，但是仍然存在，这些误差来自于滤波误差和算法本身的误差。高斯滤波精度较高，但是任何滤波算法都有误差，因此需要滤除背景的相移算法都很难实现高精度的相位计算。另外，CVM精度略高于GS、PCA2，而在前面的非理想情况下，CVM精度低于GS、PCA2，说明了CVM对背景光强、调制幅度、噪声等误差的抑制能力相对较差，而算法自身精度却比较高。

图 4. 理想情况下，针对不同类型条纹，不同相移算法的相位误差RMS值

Fig. 4. Phase errors RMS of different phase-shifting algorithms with different types of fringes in the ideal case

下载图片 查看所有图片

为了分析不同的噪声对五种算法的影响，在圆条纹的干涉图中分别添加了20 dB、30 dB、40 dB及50 dB的噪声，结果如图5所示。五种算法在任何噪声下都是有效的，无论对于哪种算法，都是噪声越大，相位误差越大。当噪声信噪比大于40 dB时，相位误差变化较小。对于任何信噪比的噪声，都是PCA&VU相位误差最小，其次是EMNSD&FLSA，第三是GS和PCA2，误差最大的是CVM。另外，当噪声信噪比为20 dB时，五种算法的相位误差相差不多。随着信噪比的增大，相位误差的差别越来越大，尤其当噪声大于40 dB时，PCA&VU和EMNSD&FLSA的优势更加明显，主要原因是它们没有滤波过程，在完美条件下，理论上可以得到完全正确的相位，因此噪声越小，精度就会有显著提高，而其他算法除了算法自身的误差外，还有滤波误差存在，无论噪声多么小，都会存在一定的相位误差。

图 5. 针对圆条纹不同相移算法在不同噪声条件下的相位误差RMS值

Fig. 5. Phase errors RMS of different phase-shifting algorithms corresponding to the circular fringes with different levels of noise

下载图片 查看所有图片

为了考查不同相移值对五种算法的影响和不同算法的有效相移范围，在非理想的背景光强、调制幅度以及20 dB噪声的条件下，模拟了相移范围为0.1~3.1 rad的干涉图，五种算法的计算结果如图6所示。对所有算法都有相同的结论：相移值越接近π/2，相位误差越小，越接近于0和π，相位误差越大。因此，如果能够设置相移值，尽量设置其接近π/2，远离0和π。对于任意相移值，PCA&VU和EMNSD&FLSA的精度始终高于GS、CVM及PCA2，并且PCA&VU的精度也始终略高于EMNSD&FLSA。在上述条件下，PCA&VU和EMNSD&FLSA的有效相移范围为0.5~2.7 rad，其他三种算法的有效相移范围为0.5~2.6 rad。噪声的存在影响了相移算法的有效相移范围，但是优秀的算法能够尽量抑制噪声的影响。

图 6. 针对圆条纹不同相移算法在不同相移值和20 dB噪声条件下的相位误差RMS值

Fig. 6. Phase errors RMS of different phase-shifting algorithms corresponding to the circular fringes with different phase shifts and 20 dB of noise

下载图片 查看所有图片

最后，对不同条纹数量进行了模拟，设置条纹数量为0.6~5，结果如图7所示。可以看出，GS、CVM及PCA2在条纹数量小于3时，相位误差不稳定，而在条纹数量大于3时，相位误差趋于稳定，尤其当条纹数量大于4时，相位误差几乎不变。对于EMNSD&FLSA和PCA&VU来说，当条纹数量大于1.4时，相位误差几乎不变。从分析结果可以看出，EMNSD&FLSA的有效条纹范围最大，为0.6~5.0，其次是PCA&VU，范围为1.0~5，最后是GS、CVM和PCA2，范围为1.2~5.0。由于EMNSD&FLSA没有滤波，而且在计算过程中没有近似，因此有效条纹范围最大。PCA&VU在计算相位初值时有近似，因此有效条纹范围受到影响，GS、CVM和PCA2的有效条纹范围最小是受到滤波算法及算法近似的影响。对于任意条纹数量，EMNSD&FLSA和PCA&VU相位误差都比其他三种算法小。值得注意的是，相移算法在条纹数量较大的时候都是适用的，因此5不是最大的条纹数量。

图 7. 针对圆条纹不同相移算法在不同条纹数量和20 dB噪声条件下的相位误差RMS值

Fig. 7. Phase errors RMS of different phase-shifting algorithms corresponding to the circular fringes with different fringe numbers and 20 dB of noise

下载图片 查看所有图片

经过上面的模拟分析，可以看出，PCA&VU和EMNSD&FLSA无论是对于圆条纹还是不规则条纹，无论是在有噪声的环境下，还是理想情况下，精度都是比较高的。在低噪声条件下，PCA&VU和EMNSD&FLSA性能更加优越，因此在实验过程中，可以采用多次测试干涉图取平均等方法尽量消除噪声，然后再利用PCA&VU和EMNSD&FLSA计算相位。在不同的相移下，PCA&VU和EMNSD&FLSA有效相移范围更大，精度也更高，在相移值接近π/2时，精度达到最高，实验过程中，可以设置相移接近π/2，远离0和π。在不同的条纹数量下，PCA&VU和EMNSD&FLSA有效条纹范围更大，尤其是EMNSD&FLSA在条纹数量低于1时，依然有效，随着条纹数量的增加，PCA&VU和EMNSD&FLSA精度很快稳定，当条纹数量大于1.4时，精度几乎对条纹数量不敏感，实验过程中，可以调整条纹数量大于2，将得到稳定的相位计算精度。在上面的所有模拟中，PCA&VU的相位计算精度都比EMNSD&FLSA略高，不仅如此，其计算时间也低于EMNSD&FLSA。综上所述，PCA&VU是一种在各种情况下，都能实现高精度、快速、稳定的相位计算的两步随机相移算法，适合高精度光学在线检测。

3 实　验

为了进一步分析和对比上述五种相移算法，采用双模快照干涉仪采集了四幅相移值分别为0、π/2、π和3π/2的干涉图，干涉图像素数为301 pixel×301 pixel。如图8所示，双模快照干涉仪采用的是偏振相机，相移误差比较小，可以利用标准四步相移算法计算出来的相位值作为参考相位值，其他相移算法计算出来的相位与参考相位之差定义为相位偏差。为了验证上面的模拟分析结果，同样采集了两组干涉图，分别是圆条纹和不规则条纹的。图9(a)和(b)分别为圆条纹和不规则条纹对应的参考相位图，图9(c)和(d)分别为采集的圆条纹和不规则条纹干涉图，经过高斯滤波后，干涉图如图9(e)和(f)所示。采用五种相移算法分别计算相位，将计算出来的相位分布与图9的参考相位分布作差作为相位偏差分布，结果如图10所示。图(a)~(e)为圆条纹的相位偏差分布图，图(f)~(j)为不规则条纹的相位偏差分布图。可以看出，无论是圆条纹还是不规则条纹，EMNSD&FLSA和PCA&VU的相位偏差RMS值都比GS、CVM和PCA2小，GS和PCA2相位偏差RMS值一致，PCA&VU相位偏差RMS值比EMNSD&FLSA略低。上面实验结果与模拟结果一致，但是实验结果有一点和模拟结果不同，对于圆条纹来说，CVM的相位偏差RMS值低于GS和PCA2，对于不规则条纹来说，结果恰好相反，而模拟结果中，无论是对于圆条纹还是不规则条纹，CVM的相位计算精度都低于GS和PCA2，CVM依赖于相移值的计算精度，从而导致其计算精度的不稳定。单纯就相位计算精度而言，文中提出的PCA&VU和EMNSD&FLSA相差不多，但是对于高精度光学检测而言，精度的小幅度提高也是有意义的。另外，笔者也对实验数据的处理时间进行了评估，如表2所示，实验干涉图的像素比模拟干涉图少，因此五种算法花费的时间更少。其他结论和模拟结果一样，文中提出的PCA&VU虽然是迭代算法，但是花费的时间却很少，针对PCA&VU高精度、少时间的特点，适合于高精度光学在线检测。

图 8. 双模快照干涉仪的实验装置图

Fig. 8. Experimental layout of dual-mode snapshot interferometry

下载图片 查看所有图片

图 9. 实验相位分布图、相移干涉图和高斯高通滤波后干涉图。 (a)、(b)圆条纹和不规则条纹对应的参考相位分布图；(c)、(d)圆条纹和不规则条纹干涉图；(e)、(f)高斯高通滤波后圆条纹和不规则条纹干涉图

Fig. 9. Experimental phase distributions, phase-shifting interferograms and interferograms after Gaussian high-pass filtering. (a), (b) Theoretical phase distributions corresponding to the circular and irregular fringes; (c), (d) Interferograms with circular and irregular fringes; (e), (f) Interferograms with circular and irregular fringes after Gaussian high-pass filtering

下载图片 查看所有图片

图 10. 不同相移算法的实验相位偏差分布图。 (a)~(e)圆条纹的相位偏差分布图； (f)~(j)不规则条纹的相位偏差分布图

Fig. 10. Experimental phase deviation distributions of different phase-shifting algorithms. (a)-(e) Phase deviation distributions of circular fringes; (f)-(j) Phase deviation distributions of irregular fringes

下载图片 查看所有图片

4 结　论

文中提出了一种基于主成分分析和VU分解法的两步随机相移算法，该算法先采用两步主成分分析法求出初始相位，然后利用没有滤波的两幅原始相移干涉图，通过VU分解法进行更高精度的相位计算。通过模拟和实验数据，对传统的、性能良好的GS、CVM、EMNSD&FLSA和文中求相位初值的PCA2及提出的PCA&VU算法进行对比，分析结果显示，对于不同的条纹类型、噪声、相移值及条纹数量，五种算法中PCA&VU精度都是最高的，而且有效相移范围和有效条纹数量范围都比GS、CVM和PCA2大，而花费时间虽然比GS和PCA2多，但是却小于0.05 s，比同为非滤波的两步随机相移算法EMNSD&FLSA还少。PCA&VU在噪声越小的情况下，优越性体现的越明显，尤其在理想情况下，能够计算出完全正确的相位，意味着该算法没有固有误差。因此，经过综合对比，PCA&VU性能最好。对于PCA&VU来说，相移值越接近π/2，相位误差越小，越接近0和π，相位误差越大，另外，当条纹数量大于2时，PCA&VU可以得到稳定的相位计算精度。因此，如果需要高的相位计算精度，最好能够提前抑制噪声，同时设置相移值远离0和π，条纹数量大于2。