基于参数化角编码的量子<i>K</i>-means算法

冯微军; 郭躬德; 林崧

doi:doi:10.3969/j.issn.1007-5461.2024.01.011

量子电子学报, 2024, 41 (1): 113, 网络出版: 2024-03-19

基于参数化角编码的量子K-means算法

Quantum K-means algorithm based on parameterized angle encoding

论文大纲

冯微军郭躬德林崧 ^*

作者单位

福建师范大学计算机与网络空间安全学院, 福建福州 350007

摘要

结合K-means算法和角编码技术, 提出了一种无需量子随机存储 (QRAM) 的量子K-means算法。该算法利用量子操作的并行性, 仅需对数数量的时间复杂度就能完成数据的加载; 并且通过对输入数据进行参数预处理操作,确定数据分量的参数阈值, 解决了样本不同特征尺度差异的问题。该算法由编码数据、相似度度量、量子最小值搜索和质心迭代更新四个主要步骤组成, 细致描述了这些步骤所涉及的算子和线路构建, 并对关键线路进行了仿真模拟。实验结果和经典预测结果一致, 验证了所提量子K-means算法的可靠性。此外, 理论分析表明所提出算法相比于经典算法在运行时间上有平方级加速。

Abstract

A quantum K-means algorithm without quantum random access memory (QRAM) is proposed by combining K-means algorithm and angle encoding technology. This algorithm makes use of parallel quantum operations and can complete data loading with only logarithmic time complexity. And by pre-processing the input data, the parameter threshold of the data components is determined, so the problem of different characteristic scales of samples can be solved according to the algorithm. The main body of the algorithm consists of four main steps: coding data, similarity measurement, quantum minimum search and centroid iterative update. The operators and circuit construction involved in these steps are described in detail. Numerical experiments based on the proposed circuit show that the results of the proposed algorithm are consistent with the classical prediction results, verifying the reliability of the quantum K-means algorithm combined with parameters. In addition, theoretical analysis shows that the proposed algorithm has square acceleration in running time compared with the classical algorithms.

0　引言

现代信息产业的高速发展以及数据的爆炸增长, 让人们对计算力的需求远远超过以往任何一个时代。IDC DataAge 2025白皮书显示, 全球数据量总和预计到 2025 年将达到 175 ZB, 因此, 数据分析迎来了巨大的挑战。早在 1982 年, Feynman^[1]提出了量子模拟的构想, 开创了量子计算这种本质上全新的计算模型。随后, Lloyd等^[2]提出了第一个量子哈密顿模拟算法, 证实了 Feynman 的构想。1985年, Deutsch^[3]提出通用容错量子计算机, 描述了图灵机的量子泛化, 证明了量子理论和通用计算机的理论是相容的, 并且可能比传统计算机具有更强的计算能力。在探寻量子优势的过程中, Deutsch^[4]在1989年首次提出了Deutsch算法, 很好地展示了量子计算机的并行性。之后Shor^[5]在1994年提出了著名的Shor算法, 证明该算法可以在多项式时间完成大数因子分解问题。1996年, Grover^[6]在经典无序搜索算法的基础上提出了Grover算法, 该算法结合了幅度放大技术, 相较于经典算法实现了平方加速。近年来, 研究人员还发现可以利用量子计算高效地完成机器学习任务, 提出了一系列量子机器学习算法, 如量子线性回归^{[7, 8]}、量子降维算法^[9-12]、量子聚类^[13-18]等。

作为机器学习的主要方法之一, 聚类分析常用于对未知类别的数据进行划分, 已广泛应用在销售、医学和生物等领域。在聚类分析中, 按照一定的规则将样本数据划分成若干个簇, 并把相似的样本聚在同一个簇中, 不相似的样本分在不同簇中。在2013年, Lloyd等^[19]提出了量子无监督学习, 指出由绝热算法实现的量子K-means算法可以在维数和样本数量参数上实现对经典K-means算法的指数加速。2019年, Kerenidis等^[20]提出了q-means算法。与经典的K-means算法相比, 该算法提供了对数据数量的指数级加速。上述算法均需使用QRAM加载样本数据, 并且需要与数据量相当的存储空间。除此之外, QRAM 尚处于理论模型阶段^[21], 在制备任意量子态方面是困难的。

本文结合角编码对数据进行加载, 基于已有样本对样本分量分别进行参数阈值设置, 执行编码数据、相似度度量、量子最小值搜索和质心迭代更新四个主要步骤。理论分析表明本文所提出算法相比于经典算法在运行时间上有平方级加速。

1　预备知识

1.1　经典K-means算法

K-means算法是一种无监督的聚类算法。给定的样本集分成K个簇, 此算法将样本集中的每一个样本依次与K个簇的质心进行距离计算, 按照距离大小确定各个样本点最近质心的簇。经典K-means算法主要分为以下四个步骤: 1) 首先选取K个(K可根据某个损失函数确定)质心, 通常是随机选取; 2) 计算余下的每一个样本点到各个质心的欧式距离, 并将其归入相互间距离最小的质心所在的簇; 3) 在所有样本点都划分完毕后, 重新计算各个簇的质心(通常是计算簇中样本点的均值), 然后迭代计算样本点到各个质心的距离, 并对所有样本点重新进行划分; 4) 重复第 2)、3) 步, 直到迭代计算后所有样本点的划分情况保持不变或小于误差, 此时K-means算法得到最优解, 将运行结果返回。

1.2　经典K-means算法相似度度量方法

经典K-means算法的关键步骤是计算待标记的样本到各个质心的距离, 并将其归入到二者间距离最小的质心所在的簇。其中, 各个簇的质心是通过计算簇中所有数据点的均值来确定的。常见的度量相似度的方式有两种, 分别是用内积计算与欧式距离计算的结果来衡量相似度。考虑两个 $N$ 维向量 $x^{(i)} = (x_{1}^{(i)}, x_{2}^{(i)}, \dots, x_{N}^{(i)})$ 和 $y = (y_{1}, y_{2}, \dots, y_{N})$ , 其基于内积的距离表达式可表示为 $|x^{j} - y| = |x^{j}| |y| - x^{j} ∙ y$ , 该距离主要关注两个向量之间的角度关系; 对于欧式距离, 其距离表达式为 $|x^{j} - y| = \sqrt[]{\sum_{i = 1}^{N} {(x_{i}^{j} - y_{i})}^{2}}$ 。这两种相似度度量方式的局限性在于特征尺度的差异将影响相似度度量。

量子K-means算法常采用欧氏距离作为度量距离的手段。该度量方式的局部较大特征将会降低较小数值特征的作用, 甚至使其根本不起作用。为了解决欧氏距离度量特征差异大的问题, 本研究在编码数据部分利用角编码对特征执行参数化预处理, 因此, 在相似度度量方面可有效避免因局部特征的数值太大而掩盖其他较小特征的情况。

1.3　本研究所提出算法涉及的量子门操作

经典计算机处理信息的基本单元是比特, 其状态为 0 或者 1。与此相似的是, 量子计算机处理的基本单元是 $|0〉$ 和 $|1〉$ , 任意经过酉算子变化的单量子比特的状态可用二维希尔伯特空间里的一个单位复向量描述, 如

|μ〉 = α_{0} |0〉 + α_{1} |1〉 = [\begin{matrix} α_{0} \\ α_{1} \end{matrix}]

,(1)

式中: $α_{0}$ 和 $α_{1}$ 是复数, 且满足 ${|α_{0}|}^{2} + {|α_{1}|}^{2} = 1$ 。

量子逻辑门是作用于单个或多个量子比特以实现某个变换的酉算子操作。本研究需要用到的单量子比特逻辑门可表示为

H = \frac{1}{\sqrt[]{2}} [\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}], R_{y} (θ) = [\begin{matrix} c o s \frac{θ}{2} & - s i n \frac{θ}{2} \\ s i n \frac{θ}{2} & c o s \frac{θ}{2} \end{matrix}]

,(2)

其中 $H$ 门主要用于创建叠加态, $R_{y} (θ)$ 门主要用于旋转数据这一步骤。常见的还有双量子逻辑门, 与文中相联系的有 $S W A P$ 门, 可表示为

S W A P = [\begin{matrix} \begin{matrix} 1 & 0 \\ 0 & 0 \end{matrix} & \begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix} \\ \begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} & \begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix} \end{matrix}]

.(3)

构建本研究需要用到受控交换门 $(C - S W A P)$ 门, 利用该量子门可以进行交换测试。不难看出, 控制量子比特为 $|1〉$ 时, 对目标比特作 $S W A P$ 操作;而处于 $|0〉$ 时, 目标量子态不变, 故而可得受控交换门为 $[\begin{matrix} I & 0 \\ 0 & S W A P \end{matrix}]$ 。需要注意的是, 矩阵中的元素都是 $4 \times 4$ 的矩阵。

最后介绍量子比较器 $(Q C M P)$ , 它一般被用作量子子程序, 此处将其作为一个算子考虑, 即

Q C M P (|M〉 \sum_{i = 1}^{N} |i〉 |0〉) = |M〉 (\sqrt[]{\frac{R}{N}} \sum_{i < M} |i〉 |1〉 + \sqrt[]{\frac{N - R}{N}} \sum_{i \geq M} |i〉 |0〉)

,(4)

2　量子算法描述

2.1　编码数据

数据角编码是制备量子态的重要方法, 可以有效地提高制备量子态的效率。在编码数据中, 本研究着重解决参数设置和数据加载这两个问题, 图1描述了由经典数据到量子线路转化的过程。

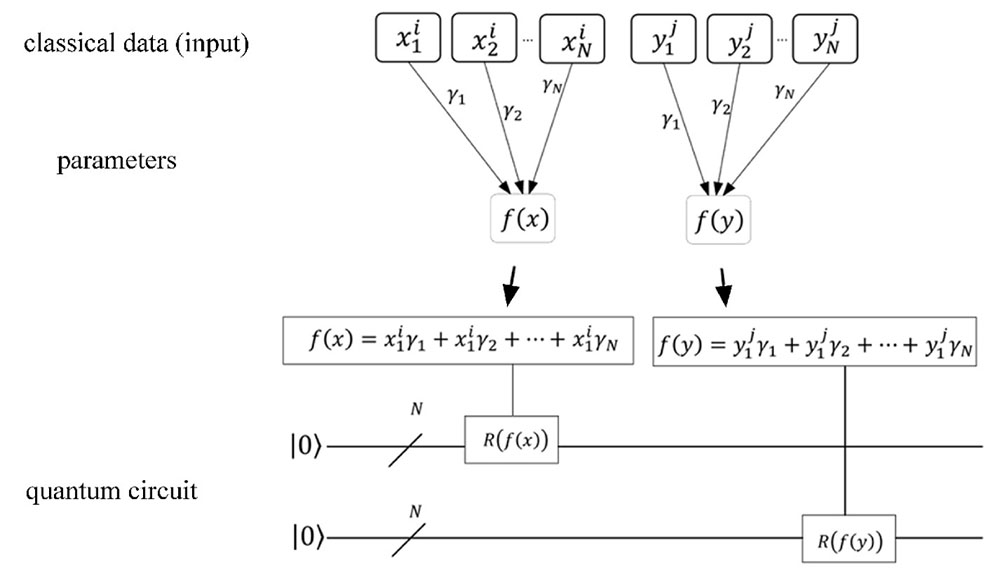
图 1. 从经典数据到量子态的量子线路图

Fig. 1. Quantum circuit diagram from classical data to quantum state

下载图片查看所有图片

首先考虑带标签的经典数据 $x^{(i)} = (x_{1}^{(i)}, x_{2}^{(i)}, \dots, x_{N}^{(i)})$ 和带有标签的质心数据 $y^{(j)} = (y_{1}^{(j)}, y_{2}^{(j)}, \dots, y_{N}^{(j)})$ 。对于所有的数据及其分量, 上标 $i$ 表示样本标签, 且 $i \in \{1,2, \dots, M\}; j$ 表示簇标签, 且 $j \in \{1,2, \dots, K\};$ 上标箭头表示经典数据;下标表示分量的位置。

步骤S1: 参数值的设定与分析

针对经典数据 $x^{(i)}$ 的各个分量, 先设定各分量对应的参数 $γ_{i}$ 。基于编码的性质^[22-24], 结合参数对数据进行编码时旋转角不超过周期 $2 π$ 。超过 $2 π$ 将无法正确计算相似度, 即对应的用Bloch球表示的旋转角度过大会影响相似度的评估。其次需要对最终相似度结果的范围进行限制, 以约束参数的范围。因此, 先规定各分量数据与阈值化参数的关系应符合 $0 \leq γ_{i} y_{i}^{(j)}, γ_{i} x_{i}^{(i)} \leq 2 π$ , 有 $γ_{i} \leq \frac{2 π}{S_{i}}$ , 其中 $S_{i} = m a x (\underset{i, j}{m a x} (x_{i}^{(i)}), y_{i}^{(j)})$ 。对数据 $x^{(i)}$ 和 $y^{(j)}$ 的分量编码分别得到量子态

\{\begin{array}{l} |x_{i}^{(i)}〉 = R_{y} (γ_{i} x_{i}^{(i)}) |0〉 = [c o s \frac{γ_{i}}{2} x_{i}^{(i)} |0〉 + s i n \frac{γ_{i}}{2} x_{i}^{(i)} |1〉] \\ |y_{i}^{(j)}〉 = R_{y} (γ_{i} y_{i}^{(j)}) |0〉 = [c o s \frac{γ_{i}}{2} y_{i}^{(j)} |0〉 + s i n \frac{γ_{i}}{2} y_{i}^{(j)} |1〉] \end{array}

.(5)

对 (5) 式的两个量子态作 $C - S W A P$ 操作, 便可得到任意分量 $x_{i}^{(i)}$ 和 $y_{i}^{(j)}$ 分量之间的保真度为 $c o s^{2} \frac{γ_{i}}{2} (x_{i}^{(i)} - y_{i}^{(j)})$ , 此处蕴含单调关系 $- \frac{π}{2} \leq \frac{γ_{i}}{2} (x_{i}^{(i)} - y_{i}^{(j)}) \leq \frac{π}{2}$ , 即 $γ_{i} \leq \frac{π}{|x_{i}^{(i)} - y_{i}^{(j)}|}$ 。因此, 先设定 $T_{i} = \underset{i, j}{m a x} |x_{i}^{(i)} - y_{i}^{(j)}|$ , 进一步令 $L_{i} = m a x (S_{i}, 2 T_{i})$ , 可得表达式 $γ_{i} \equiv \frac{2 π}{L_{i}}$ 。此处, 参数 $γ_{i}$ 的设定最终确定特征缩放的范围, 解决了不同特征间的尺度问题。最后, 分别记编码质心和待分配样本的算子为 $U (γ; y^{(j)}) \equiv \overset{N}{\underset{i^{'} = 1}{\otimes}} R_{y} (γ_{i^{'}} y_{i^{'}}^{(j)})$ 和 $U (γ; x^{(i)}) \equiv \overset{N}{\underset{i^{'} = 1}{\otimes}} R_{y} (γ_{i^{'}} x_{i^{'}}^{(i)})$ 。

步骤S2: 经典数据的加载

利用酉算子 $U (γ; y^{(j)})$ 编码质心 $y^{(j)}$ , 得到量子态

|y^{(j)}〉 = (\overset{N}{\underset{i^{'} = 1}{\otimes}} R_{y} (γ_{i^{'}} y_{i^{'}}^{(j)})) |0 \dots 0〉 = \overset{N}{\underset{i^{'} = 1}{\otimes}} [c o s \frac{γ_{i^{'}}}{2} y_{i^{'}}^{(j)} |0〉 + s i n \frac{γ_{i^{'}}}{2} y_{i^{'}}^{(j)} |1〉]

,(6)

同理, 用相同的方式对向量 $x^{(i)}$ 编码可以得到

|x^{(i)}〉 = (\overset{N}{\underset{i^{'} = 1}{\otimes}} R_{y} (γ_{i^{'}} x_{i^{'}}^{(i)})) |0 \dots 0〉 = \overset{N}{\underset{i^{'} = 1}{\otimes}} [c o s \frac{γ_{i^{'}}}{2} x_{i^{'}}^{(i)} |0〉 + s i n \frac{γ_{i^{'}}}{2} x_{i^{'}}^{(i)} |1〉]

,(7)

然后, 初始化量子寄存器1、2为 ${|0〉}_{1}^{\otimes l o g_{2} K} 、 {|0〉}_{2}^{\otimes l o g_{2} M}$ , 用于构建条件受控的算子。与利用QRAM模型对数据的加载方式不同, 本研究以算子的方式将数据载入量子态中。再附加两个量子寄存器 ${|0〉}_{3}^{\otimes N}$ 、 ${|0〉}_{4}^{\otimes N}$ , 根据参考文献 [25] 对受控量子门的描述, 用量子寄存器1、2分别控制量子寄存器3、4对数据的载入。量子寄存器1控制量子寄存器3的算子形式为

U_{γ y} \equiv U_{1} (γ; y^{(1)}) ⨁ \dots ⨁ U_{K} (γ; y^{(K)}) \equiv {[\begin{matrix} U_{1} (γ; y^{(1)}) & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & U_{K} (γ; y^{(K)}) \end{matrix}]}_{(K \times 2^{N}) \times (K \times 2^{N})}

.(8)

$同理, 量子寄存器 2 控制量子寄存器 4 的算子 U_{γ x} 与 (8) 式形式类似, 都是通过条件受控构建的。$ $U_{γ y}$ 和 $U_{γ x}$ 算子的构建依赖于叠加态 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} |j〉、 \frac{1}{\sqrt[]{M}} \sum_{i = 1}^{M} |i〉$ 的制备^[26]。制备过程用到 $H$ 门、受控酉门和量子比较器子程序。利用量子寄存器1控制编码算子 $U (γ; y^{(j)})$ , 实现了对质心叠加态的制备。 $U_{γ y}$ 对量子寄存器3的加载表现为

U_{γ y} (\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} {|0〉}_{3}^{\otimes N}) = \frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} U_{j} (γ; y^{(j)}) {|0〉}_{3}^{\otimes N}

.(9)

上述操作后, 利用量子寄存器2控制编码算子 $U (γ; x^{(i)})$ 可得到状态 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} {(\overset{N}{\underset{i^{'} = 1}{\otimes}} (c o s \frac{γ_{i^{'}}}{2} y_{i^{'}}^{(j)} |0〉 + s i n \frac{γ_{i^{'}}}{2} y_{i^{'}}^{(j)} |1〉))}_{3} {(\overset{N}{\underset{i^{'} = 1}{\otimes}} [c o s \frac{γ_{i^{'}}}{2} x_{i^{'}}^{(i)} |0〉 + s i n \frac{γ_{i^{'}}}{2} x_{i^{'}}^{(i)} |1〉])}_{4}$ 。为了便于分析, 将其化简为 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} {|y^{(j)}〉}_{3} {|x^{(i)}〉}_{4}$ , 其中 $|y^{(j)}〉$ 表示量子寄存器3, $|x^{(i)}〉$ 表示量子寄存器4。

2.2　相似度度量

K-means算法的一个关键步骤是估计测试样本与质心之间的相似度, 着重解决测试样本与质心之间距离的问题。为计算样本之间的相似度, 本研究采用了多量子比特交换测试线路^[27]。

步骤S3: 多量子比特交换测试的实现

首先初始化长度为 $l$ 的量子寄存器5, 利用 $H^{\otimes l}$ 门制备叠加态 $\frac{1}{\sqrt[]{2^{l}}} \sum_{q = 0}^{2^{l} - 1} |q〉$ , 其中 $l = ⌈l o g_{2} N + 1⌉$ 。对量子寄存器5中 $q$ 的可能输出值做经典预处理, 具体过程如下: 1)对 $q$ 值做取模运算, 以 $x$ 值代替取模值, 即 $x = q m o d 4$ ; 2) 将步骤1) 中的 $x$ 值代入函数 $f (x) = \frac{x^{2} - 3 x + 2}{2}$ , 得到映射值0或1; 3) 将所有映射值为1的 $q$ 值用二进制表示, 用来控制构建受控 $S W A P$ 门。

以3量子比特为例构建多量子比特交换测试线路, 如图2所示。

图 2. 3-辅助量子比特的线路示意图

Fig. 2. Circuit diagram with 3-auxiliary qubits

下载图片查看所有图片

推广到 $l$ 个控制量子比特, 则图2标记的算子数量为 $2^{l - 1}$ , 每一个算子可用

U_{p} = \{\begin{matrix} \begin{matrix} (|4 t〉 〈4 t| \otimes I_{4 t} \otimes S W A P_{2} + \sum_{i \neq 4 t} |q〉 〈q| \otimes I_{4 t + 2}) \otimes I_{2 N - 4 t - 2}, & i f p = 4 t \end{matrix} \\ \begin{matrix} (|3 + 4 t〉 〈3 + 4 t| \otimes I_{2 + 4 t} \otimes S W A P_{2} + \sum_{i \neq 4 t + 3} |q〉 〈q| \otimes I_{4 + 4 t}) \otimes I_{2 N - 4 t - 4}, & i f p = 3 + 4 t \end{matrix} \\ \begin{matrix} I_{2 N + l} & o t h e r w i s e \end{matrix} \end{matrix}

(10)

表示, 其中算子下标表示量子比特数。由步骤S2可得量子态 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} {|y^{(j)}〉}_{3} {|x^{(i)}〉}_{4}$ , 在此基础上增加一个寄存器5, 初始化为 ${|0〉}^{\otimes l}$ , 并执行多量子比特交换测试。先通过 $H^{\otimes l}$ 将寄存器5转换为叠加态, 得到量子态 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} {|y^{(j)}〉}_{3} {|x^{(i)}〉}_{4} {(\frac{1}{\sqrt[]{2^{l}}} \sum_{q = 0}^{2^{l} - 1} |q〉)}_{5}$ 。下一步, 执行多量子比特交换测试以获得相似度度量的结果。为了方便表示, 记(10)式所有受控酉门的乘积形式为

U_{η} = U_{2 N - 1} U_{2 N - 2} \dots U_{1} U_{0}

,(11)

式中算子 $U_{η}$ 中有一半是多维单位阵。在执行完受控交换测试操作之后, 将得到量子态 $\frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} (I_{2 N} \otimes H^{\otimes l}) U_{η} ({|y^{(j)}〉}_{3} {|x^{(i)}〉}_{4} {(\frac{1}{\sqrt[]{2^{l}}} \sum_{q = 0}^{2^{l} - 1} |q〉)}_{5})$ 。测量量子比特 $|q_{l}〉$ , 可以得到关于 $P (|q_{l}〉 = |0〉)$ 的概率分布, 用来衡量质心 $y^{(j)}$ 和样本 $x^{(i)}$ 的相似度, 即

P (|q_{l}〉 = |0〉) = \frac{[\frac{1}{2^{l - 1}} \sum_{i^{'} = 0}^{2^{l - 1} - 1} c o s^{2} \frac{γ_{i^{'}}}{2} (x_{i^{'}}^{(i)} - y_{i^{'}}^{(j)})] + 1}{2} = \frac{[\frac{1}{N} \sum_{i^{'} = 0}^{N - 1} c o s^{2} \frac{γ_{i^{'}}}{2} (x_{i^{'}}^{(i)} - y_{i^{'}}^{(j)})] + 1}{2}

,(12)

式中 $N = 2^{l - 1}$ 表示维度。根据量子比特 $|q_{l}〉$ 的测量结果, 可以将相似度度量的结果改写为

|ψ_{0}〉 = \frac{1}{\sqrt[]{K}} \sum_{j = 1}^{K} {|j〉}_{1} \frac{1}{\sqrt[]{M}} \sum_{j = 1}^{M} {|i〉}_{2} (s i n θ_{j i} |u_{j i}〉 |0〉 + c o s θ_{j i} |v_{j i}〉 |1〉)

,(13)

式中 $|0〉$ 、 $|1〉$ 表示量子寄存器5第 $l$ 量子位 $q_{l}$ 的量子状态, $|u_{j i}〉、 |v_{j i}〉$ 是两个复杂的量子态, 在分析过程中可忽略其具体形式。

步骤S4: 多量子相位估计

该步骤利用量子相位估计来获得所有 $θ_{j i}$ 信息。为完成估计信息的任务, 还需要制备酉算子 $G = \prod_{j i} V_{j i}$ , 过程如下:

1) 基于已定义的酉算子 $U_{η}$ 、 $U (γ; x^{(i)})$ 、 $U (γ; y^{(j)})$ 来构建受控算子, 即对于所有标签 $|j i〉$ , 定义以下控制算子

\sum_{j i} V_{j i} \equiv \sum_{j i} |j i〉 〈j i| \otimes \{[I_{2 N} \otimes H^{\otimes l}] U_{η} [I_{2 N} \otimes H^{\otimes l}] [U (γ; x^{(i)}) \otimes U (γ; y^{(j)}) \otimes I_{l}]\} (H^{\otimes l o g_{2} K + l o g_{2} M} \otimes I_{2 N + l}) .

(14)

2) 将控制算子 $\sum_{j i} V_{j i}$ 作用于初始态 ${|0〉}_{l o g_{2} K + l o g_{2} M} {|0〉}_{2 N + l}$ , 于是整个系统将处于

|ψ_{0}〉 = \sum_{j i} V_{j i} {|0〉}_{l o g_{2} K + l o g_{2} M} {|0〉}_{2 N + l} = \frac{1}{\sqrt[]{K M}} \sum_{j i} |j i〉 (s i n θ_{j i} |u_{j i}〉 |0〉 + c o s θ_{j i} |v_{j i}〉 |1〉)

\frac{1}{\sqrt[]{K M}} \sum_{j i} \frac{- i}{\sqrt[]{2}} (e^{i θ_{j i}} |ω_{j i +}〉 - e^{- i θ_{j i}} |ω_{j i -}〉)

,(15)

式中 $|ω_{j i \pm}〉$ 表示 $\frac{1}{\sqrt[]{2}} |u_{j i}〉 |0〉 \pm \frac{i}{\sqrt[]{2}} |v_{j i}〉 |1〉$ 。

3) 由文献 [28], 可以构建迭代酉算子

G = \sum_{j i} V_{j i} (I^{\otimes l o g_{2} K + l o g_{2} M} \otimes (I^{\otimes 2 N + l} - 2 ({|0〉}^{\otimes (2 N + l)} 〈0|))) {\sum_{j i} V_{j i}}^{†} (I^{\otimes l o g_{2} K + l o g_{2} M + 2 N + l - 1} \otimes Z_{q_{l}})

,(16)

使得 $G$ 作用到状态 $|ψ_{0}〉$ , 将产生新的的量子态

|ψ_{1}〉 = G |ψ_{0}〉 = \frac{1}{\sqrt[]{K M}} \sum_{j i} |j〉 |i〉 (s i n 3 θ_{j i} |u_{j i}〉 |0〉 + c o s 3 θ_{j i} |v_{j i}〉 |1〉)

.(17)

因此, 在给定量子态 $|ψ_{0}〉$ 以及迭代酉算子 $G = \prod_{i, j} V_{j i}$ 的条件下, 下一步可以执行多量子相位估计, 并将所有 $θ_{j i}$ 的信息转到新的量子寄存器中。首先附加精度为 $t$ 的量子寄存器6, 利用 $G$ 做量子相位估计^[29], 并对算法的结果进行分析得到量子态

|ψ_{2}〉 = \frac{- i}{\sqrt[]{2 M K}} \sum_{j = 1}^{K} \sum_{i = 1}^{M} [e^{i θ_{j i}} |2^{t} \frac{θ_{j i}}{π}〉 |j i〉 |ω_{j i +}〉 - e^{- i θ_{j i}} |2^{t} (1 - \frac{θ_{j i}}{π})〉 |j i〉 |ω_{j i -}〉]

,(18)

此式表示任意标签 $j i$ 分别对应两种输出结果, 即 $|2^{t} \frac{θ_{j i}}{π}〉$ 和 $|2^{t} (1 - \frac{θ_{j i}}{π})〉$ 。多量子相位估计线路如图3所示, 其中 $Q F T^{†}$ 表示逆傅里叶变换。最后可在量子寄存器6得到二进制序列, 用于表示样本 $i$ 和质心 $j$ 的相似度信息。

图 3. 多量子相位估计线路图

Fig. 3. Circuit diagram of multi-quantum phase estimation

下载图片查看所有图片

步骤S5: 转移相位估计信息

根据(12)式保真度公式的结果 $\frac{1}{N} \sum_{i^{'} = 0}^{N - 1} c o s^{2} \frac{γ_{i^{'}}}{2} (x_{i^{'}}^{(i)} - y_{i^{'}}^{(j)}) = 1 - 2 c o s^{2} (θ_{j i})$ , 以及条件 $θ_{j i} \in [\frac{π}{4}, \frac{3 π}{4}], |c o s θ_{j i}|$ 愈大则保真度愈小。下一步是实现量子寄存器6信息的转化, 首先附加量子寄存器7, 然后利用量子寄存器6控制量子寄存器7从而得到相位信息的转化结果。为了保证在同一个标签上输出的信息是一致的, 利用量子线路构建 $|c o s θ_{j i}|$ 函数。当输入是 $\frac{θ_{j i}}{π}$ 和 $1 - \frac{θ_{j i}}{π}$ 时, 输出值对应 $|c o s θ_{j i}|$ 。下一步构建量子余弦函数线路^[30], 利用量子线路并行求解 $|c o s θ_{j i}|$ , 得到量子态

\frac{- i}{\sqrt[]{2 K M}} \sum_{j = 1}^{K} \sum_{i = 1}^{M} [e^{i θ_{j i}} |2^{t} \frac{θ_{j i}}{π}〉 |j i〉 |ω_{j i +}〉 - e^{- i θ_{j i}} |2^{t} (1 - \frac{θ_{j i}}{π})〉 |j i〉 |ω_{j i -}〉] {||c o s θ_{j i}|〉}_{7}

其中 $||c o s θ_{j i}|〉$ 是数值 $|c o s θ_{j i}|$ 二进制的多量子表示形式。由此, 成功创建了一个存储质心与样本之间相似度信息的量子叠加态。

2.3　量子最小值搜索

为方便起见, 将2.2节最终得到的量子态简化为 $\frac{1}{\sqrt[]{K M}} \sum_{j = 1}^{K} {|j〉}_{1} \sum_{i = 1}^{M} {|i〉}_{2} {||c o s θ_{j}|〉}_{7}$ , 本节将利用量子最小值搜索算法^[31]对其进行步骤描述。

步骤S6: 量子最小值搜索算法求最小值标签

1) 随机初始化一个标签, 确定其量子寄存器1、2的大小。针对量子态 $\frac{1}{\sqrt[]{K M}} \sum_{j = 1}^{K} {|j〉}_{1} \sum_{i = 1}^{M} {|i〉}_{2} {||c o s θ_{j i}|〉}_{7}$ , 随机初始化一个阈值标签 $j i$ , 并将对应量子寄存器7的值设定为 $y$ 。附加一个寄存器, 记作 $\frac{1}{\sqrt[]{K M}} \sum_{j = 1}^{K} {|j〉}_{1} \sum_{i = 1}^{M} {|i〉}_{2} {||c o s θ_{j i}|〉}_{7} {|y〉}_{8}$ 。

2) 利用 $Q C M P$ ^[32]作用于量子寄存器7和8。附加一个量子寄存器9存储标记信息, 得到

$\frac{1}{\sqrt[]{K M}} (\sum_{j \in G} {|j〉}_{1} \sum_{i = 1}^{M} {|i〉}_{2} {||c o s θ_{j i}|〉}_{7} {|y〉}_{8} {|1〉}_{9} + \sum_{j \notin G} {|j〉}_{1} \sum_{i = 1}^{M} {|i〉}_{2} {||c o s θ_{j i}|〉}_{7} {|y〉}_{8} {|0〉}_{9})$ , 其中 $G$ 表示 $||c o s θ_{j i}|〉$ 小于阈值 $|y〉$ 的标签集合, 此时将量子寄存器9置为 $|1〉$ , 否则置为 $|0〉$ 。

3) 利用Qsearch算法^[33]搜索量子寄存器9是否处于 $|1〉$ 。如果处于 $|0〉$ , 则直接输出量子寄存器8对应的结果;否则读取量子寄存器7的信息, 并将该信息赋值到量子寄存器8, 以重新确定新一轮循环的状态。

4) 根据文献[31]的结论, 当总时间复杂度小于 $O (22.5 \sqrt[]{K M} + 1.4 l o g_{2}^{2} K M)$ , 重复步骤2) 和 3); 否则直接读取索引。

利用上述步骤可以得到待分配样本点所归属的簇标签。

2.4　质心迭代更新

将所有样本点分配到簇的过程会影响数据点的分布, 进而改变质心的位置, 因此, 在完成一轮迭代后需要重新考虑聚类效果。在聚类过程, 若样本点均匀分布在质心周围, 不影响质心分布的稳定性; 若样本点非均匀分布在质心周围, 则需要重新计算质心, 并对所有样本重新聚类。考虑到数据集在一轮迭代中可能改变原质心位置的情况, 就需要重新计算簇的质心。若需要对簇中样本计算新的质心, 这必然会导致质心计算的复杂度增加。为解决质心计算的问题引入了随机采样方案, 此方案利用量子的概率性输出簇中样本子集并近似代表质心, 可以降低计算质心的复杂度。

对每个簇进行随机采样之前, 记原始的簇大小为 $|C^{j}|$ , 任一经过随机采样的簇的大小记为 $|\tilde{C^{j}}|$ , 满足关系式 $|\tilde{C^{j}}| \leq |C^{j}|$ 。质心迭代涉及到对所有新质心的计算, 并用随机采样的样本均值表示新质心。在计算得到新质心后, 需要重新按照2.1～2.4中的步骤对所有样本进行聚类操作。

3　性能分析

3.1　复杂度分析

在数据编码部分, 量子寄存器1、2 创建叠加态的时间复杂度为 $O (l o g_{2} K + l o g_{2} M)$ , 故可将整个编码数据部分的时间复杂度记为 $O (l o g_{2} K M)$ 。在步骤 S3 中, 其时间复杂度集中在 $U_{η} = U_{2 N - 1} U_{2 N - 2} \dots U_{1} U_{0}$ , 故为 $O (N)$ 。针对多量子相位估计步骤, 酉算子 $G$ 对应的时间复杂度为 $O (l o g_{2} K M [l o g_{2} K M + N])$ 。另外, 相位估计的复杂度还和量子寄存器6的精度 $t$ 相关, 这意味着当精度 $t$ 远小于样本维数 $N$ 或者 $t ≪ l o g_{2} K M$ , 整个多量子相位估计的时间复杂度为 $O (l o g_{2} K M [l o g_{2} K M + N])$ 。下一步来分析量子绝对值余弦函数 $|c o s θ_{j i}|$ , 对函数进行模块化处理, 其时间复杂度与数据维度及训练集大小无关, 所以时间复杂度记为 $O (1)$ 。2.3节分析了量子最小值搜索的算法过程, 并给出执行该步骤的时间复杂度为 $O (22.5 \sqrt[]{K M} + 1.4 l o g_{2}^{2} (K M))$ 。所以, 样本分配到簇的时间复杂度记为 $O (l o g_{2} K M [l o g_{2} K M + N] [22.5 \sqrt[]{K M} + 1.4 l o g_{2}^{2} (K M)])$ , 并且可以进一步简化为 $O (l o g_{2} K M [l o g_{2} K M + N] \sqrt[]{K M})$ 。

经典K-means算法、本算法和其他量子K-means算法时间复杂度对比如表1 所示, 表中时间复杂度表示一轮迭代的总时间复杂度, 其中 $M$ 表示样本数、 $η$ 是样本最大平方范数、 $δ$ 是误差参数。需要注意的是, 在经典K-means算法中还涉及对各个簇质心的计算。Lloyd 的算法实现了对维数和样本数的指数加速, Kerenidis 的算法实现了对样本数的指数加速, 二者算法的加速效果都是基于 QRAM 模型实现的。

表 1. K-means算法之间的比较

Table 1. Comparison between K-means algorithms

Algorithm	Implementation mode	Time complexity
Classical K-means algorithm	/	$O (K M N)$
The proposed algorithm	Angle encoding	$O ((N + p o l y (l o g_{2} K M)) \sqrt[]{K M})$
Lloyd'algorithm^[19]	QRAM	$O (l o g_{2} K M N)$
Kerenidis'algorithm^[20]	QRAM	$O (\frac{K^{2} N η^{2.5}}{δ^{3}} p o l y (l o g M))$

查看所有表

3.2　数值实验

为了更加直观地判断样本的归属, 以二维样本 $y$ (3, 30) 和质心 $x^{1}$ (8, 70)、 $x^{2}$ (2, 25) 为例进行数值实验。按照经典方式计算经预处理的数据, 样本点 $y$ 与质心点 $x^{2}$ 的相似度更高。图4是该例在 $q a s m$ 量子模拟器上运行的实验结果分布图。针对低维样本数据的相似度度量任务, 由条形图的概率分布可计算出相似度度量结果。

图 4. 二维数据点到两个质心的概率分布

Fig. 4. Probability distribution of two-dimensional data points to two centroids

下载图片查看所有图片

由图4可见, 第7量子比特表示对应标签所取得概率是大致相等的, 各接近50%。在测得量子寄存器 7结果为 1 情况下, 发现分别对第 2 个量子寄存器测得 0/1 的概率波动较大, 这意味着样本 $y$ 和质心 $x^{1}$ 之间的相似度较低, 使得二者测量概率接近; 在测得量子寄存器 7 为 0 的条件下, 所得第 2 量子寄存器为 0 的概率 $P (0)$ 远大于其概率为 1 的概率 $P (1)$ , 这表明样本 $y$ 和质心 $x^{2}$ 非常接近, 使得测量的概率差别较大, 由(12)式还可以计算出样本和质心相似度的大小。计算可得: 样本 $y$ 和质心 $x^{2}$ 相似度为95.02%, 而和质心 $x^{1}$ 的相似度为10.04%。因此, 本研究所涉及线路可用于计算样本 $y$ 与质心 $x^{2}$ 的相似度, 并且该结果与经典计算得到的预测结果一致。

4　结论

提出了一种无需QRAM存储的量子K-means算法。该算法利用角编码技术将经典数据转化为量子态, 并且对输入的经典数据施加不同参数, 从而解决样本不同特征尺度差异的问题。在相似度度量步骤, 使用多量子比特交换测试及量子相位估计算法, 以估计样本与质心之间的相似度信息; 在量子最小值搜索阶段, 将量子最小值搜索算法用于求解待分配样本点所归属的簇标签; 最后, 通过概率性输出样本子集近似代表质心。时间复杂度分析结果表明, 所提出算法相较于经典K-means算法实现了样本数的平方加速。还利用角编码加载了已预处理的数据, 由数值实验得出的相似度结果与经典结果一致。此外, 虽然本算法无法达到其他量子K-means算法的指数级加速效果, 但其可有效实现特征权重不同的数据集的聚类任务, 具有更广泛的适用范围。除了特征权重不同, 数据集的分布情况也是影响聚类效果的另一个主要因素。例如, 现有量子K-means算法对非凸数据集无法进行有效聚类分析。因此, 如何设计高效的量子K-means算法来解决非典型数据分布的数据集聚类问题将是下一步研究的重点。

参考文献

[1] Feynman R P. Simulating physics with computers[J]. International Journal of Theoretical Physic, 1982, 21(6): 467-488.

[2] Lloyd S, Mohseni M, Rebentrost P. Quantum principal component analysis[J]. Nature Physics, 2014, 10(9): 631-633.

[3] DeutschD. Quantum theory, the Church–Turing principle and the universal quantum computer [C]. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 1985: 97-117.

[4] DeutschD E. Quantum computational networks [C]. Proceedings of The Royal Society of London. A. Mathematical and Physical Sciences, 1989: 73-90.

[5] ShorP W. Algorithms for quantum computation: discrete logarithms and factoring [C]. Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, USA, IEEE, 1994: 124-134.

[6] GroverL K. A fast quantum mechanical algorithm for database search [C]. Proceedings of The Twenty-eighth Annual ACM Symposium on Theory of Computing, Philadelphia, USA, ACM, 1996: 212-219.

[7] Zhang D B, Xue Z Y, Zhu S L, et al. Realizing quantum linear regression with auxiliary qumodes[J]. Physical Review A, 2019, 99(1): 012331.

[8] GilyénA, SongZ, TangE. An improved quantum-inspired algorithm for linear regression [OL]. arXiv: 2009.07268, 2020, https://arxiv.org/abs/2009.07268.

[9] Sornsaeng A, Dangniam N, Palittapongarnpim P, et al. Quantum diffusion map for nonlinear dimensionality reduction[J]. Physical Review A, 2021, 104(5): 052410.

[10] Duan B J, Yuan J B, Xu J, et al. Quantum algorithm and quantum circuit for A-optimal projection: Dimensionality reduction[J]. Physical Review A, 2019, 99(3): 032311.

[11] Lin J, Bao W S, Zhang S, et al. An improved quantum principal component analysis algorithm based on the quantum singular threshold method[J]. Physics Letters A, 2019, 383(24): 2862-2868.

[12] He C, Li J Z, Liu W Q, et al. A low-complexity quantum principal component analysis algorithm[J]. IEEE Transactions on Quantum Engineering, 2022, 3: 1-13.

[13] 陈梦涵, 郭躬德, 林崧. 基于汉明距离的量子推荐算法[J]. 量子电子学报, 2021, 38(3): 332-340.

Chen M H, Guo G D, Lin S. Quantum recommendation algorithm based on Hamming distance[J]. Chinese Journal of Quantum Electronics, 2021, 38(3): 332-340.

[14] Fan D C, Song Z L, Jon S, et al. An improved quantum clustering algorithm with weighted distance based on PSO and research on the prediction of electrical power demand[J]. Journal of Intelligent & Fuzzy Systems, 2020, 38(2): 2359-2367.

[15] Yu K, Guo G D, Li J, et al. Quantum algorithms for similarity measurement based on Euclidean distance[J]. International Journal of Theoretical Physics, 2020, 59(10): 3134-3144.

[16] Gong C Q, Dong Z Y, Gani A, et al. Quantum K-means algorithm based on trusted server in quantum cloud computing[J]. Quantum Information Processing, 2021, 20(4): 1-22.

[17] Wu Z H, Song T T, Zhang Y B. Quantum K-means algorithm based on Manhattan distance[J]. Quantum Information Processing, 2022, 21(1): 19.

[18] KhanS U, AwanA J, Vall-LloseraG. K-means clustering on noisy intermediate scale quantum computers [OL]. arXiv: 1909.12183, 2019, https://arxiv.org/abs/1909.12183.

[19] LloydS, MohseniM, RebentrostP. Quantum algorithms for supervised and unsupervised machine learning [OL]. arXiv: 1307. 0411, 2013, https://arxiv.org/abs/1307.0411.

[20] KerenidisI, LandmanJ, LuongoA, et al. q-means: A quantum algorithm for unsupervised machine learning [C]. Proceedings of the 32nd Advances in Neural Information Processing Systems, Montreal, Canada, 2019: 4136–4146.

[21] 黄一鸣, 雷航, 李晓瑜. 量子机器学习算法综述[J]. 计算机学报, 2018, 41(1): 145-163.

Huang Y M, Lei H, Li X Y. A survey on quantum machine learning[J]. Chinese Journal of Computers, 2018, 41(1): 145-163.

[22] 臧一鸣, 朱尚超, 魏战红, 等. 一种量子图像伪彩色编码方法[J]. 量子电子学报, 2022, 39(3): 343-353.

Zang Y M, Zhu S C, Wei Z H, et al. A pseudo color coding method for quantum image[J]. Chinese Journal of Quantum Electronics, 2022, 39(3): 343-353.

[23] WeigoldM, BarzenJ, LeymannF, et al. Expanding data encoding patterns for quantum algorithms [C]. 2021 IEEE 18th International Conference on Software Architecture Companion (ICSA-C), Stuttgart, Germany, 2021: 95-101.

[24] SchuldM. Supervised quantum machine learning models are kernel methods [OL]. 2021, arXiv: 2101.11020, https://arxiv.org/abs/2101.11020.

[25] WilliamsC P. Explorations in Quantum Computing [M]. 2nd ed., New York: Springer, 2011: 83-91.

[26] Dang Y J, Jiang N, Hu H, et al. Image classification based on quantum K-Nearest-Neighbor algorithm[J]. Quantum Information Processing, 2018, 17(9): 239.

[27] Li P C, Guo J H, Wang B, et al. Quantum circuits for calculating the squared sum of the inner product of quantum states and its application[J]. International Journal of Quantum Information, 2019, 17(5): 1950043.

[28] Zhao J, Zhang Y H, Shao C P, et al. Building quantum neural networks based on a swap test[J]. Physical Review A, 2019, 100(1): 012334.

[29] Li P, Wang B. Quantum neural networks model based on swap test and phase estimation[J]. Neural Networks, 2020, 130: 152-164.

[30] Wang S B, Wang Z M, Li W D, et al. Quantum circuits design for evaluating transcendental functions based on a function-value binary expansion method[J]. Quantum Information Processing, 2020, 19(10): 347.

[31] QuekY, CanonneC, RebentrostP. Robust quantum minimum finding with an application to hypothesis selection [OL]. 2020, arXiv: 2003.11777, https://arxiv.org/abs/2003.11777.

[32] Xia H Y, Li H S, Zhang H, et al. An efficient design of reversible multi-bit quantum comparator via only a single ancillary bit[J]. International Journal of Theoretical Physics, 2018, 57(12): 3727-3744.

[33] Brassard G, Høyer P, Mosca M, et al. Quantum amplitude amplification and estimation[J]. Contemporary Mathematics, 2002, 305: 53-74.

0　引言

1　预备知识

1.1　经典K-means算法

1.2　经典K-means算法相似度度量方法

冯微军, 郭躬德, 林崧. 基于参数化角编码的量子K-means算法[J]. 量子电子学报, 2024, 41(1): 113. Weijun FENG, Gongde GUO, Song LIN. Quantum K-means algorithm based on parameterized angle encoding[J]. Chinese Journal of Quantum Electronics, 2024, 41(1): 113.

基于参数化角编码的量子K-means算法

0　引言

1　预备知识

1.1　经典K-means算法

1.2　经典K-means算法相似度度量方法

1.3　本研究所提出算法涉及的量子门操作

2　量子算法描述

2.1　编码数据

图 1. 从经典数据到量子态的量子线路图

Fig. 1. Quantum circuit diagram from classical data to quantum state

2.2　相似度度量

图 2. 3-辅助量子比特的线路示意图

Fig. 2. Circuit diagram with 3-auxiliary qubits

图 3. 多量子相位估计线路图

Fig. 3. Circuit diagram of multi-quantum phase estimation

2.3　量子最小值搜索

2.4　质心迭代更新

3　性能分析

3.1　复杂度分析

表 1. K-means算法之间的比较

Table 1. Comparison between K-means algorithms

3.2　数值实验

图 4. 二维数据点到两个质心的概率分布

Fig. 4. Probability distribution of two-dimensional data points to two centroids

4　结论

Article Outline

关于本站 Cookie 的使用提示

全站搜索

基于参数化角编码的量子K-means算法

0 引言

1 预备知识

1.1 经典K-means算法

1.2 经典K-means算法相似度度量方法

1.3 本研究所提出算法涉及的量子门操作

2 量子算法描述

2.1 编码数据

图 1. 从经典数据到量子态的量子线路图

Fig. 1. Quantum circuit diagram from classical data to quantum state

2.2 相似度度量

图 2. 3-辅助量子比特的线路示意图

Fig. 2. Circuit diagram with 3-auxiliary qubits

图 3. 多量子相位估计线路图

Fig. 3. Circuit diagram of multi-quantum phase estimation

2.3 量子最小值搜索

2.4 质心迭代更新

3 性能分析

3.1 复杂度分析

表 1. K-means算法之间的比较

Table 1. Comparison between K-means algorithms

3.2 数值实验

图 4. 二维数据点到两个质心的概率分布

Fig. 4. Probability distribution of two-dimensional data points to two centroids

4 结论

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

0　引言

1　预备知识

1.1　经典K-means算法

1.2　经典K-means算法相似度度量方法

1.3　本研究所提出算法涉及的量子门操作

2　量子算法描述

2.1　编码数据

2.2　相似度度量

2.3　量子最小值搜索

2.4　质心迭代更新

3　性能分析

3.1　复杂度分析

3.2　数值实验

4　结论