1 引　言

光纤形状传感是近年来一个新的研究方向，该技术在航天变形翼形状监测、手术导管跟踪、长距离电缆变形监测等场合都具有较高的应用价值^[1-2]。光频域反射法（optical frequency domain reflectometry, OFDR）可以做到分布式测量，利用铺设在被测物体上的光纤，采用分布式测量光纤曲率的方法，通过一定的算法测量物体的形状和位置，具有较高的空间分辨率。由于多芯光纤适用于大曲率情况，具有芯间各项同性等优点，研究其重构算法具有很大意义。

Miller等^[3]提出将光纤近似划分为圆弧，根据密切圆理论重构算法由分布式应变测量数据研究二维光纤形状传感。 Duncan等^[4]结合OFDR技术，在一根1.1 m的多芯光纤上蚀刻光纤布拉格光栅（fiber Bragg grating， FBG），实现了空间分辨率为1 cm的二维和三维传感。Moore等^[5]采用基于空间微分几何的Frenet框架，将FBG传感器置于多芯光纤中测量应变值，用数值方法求解相应方程，从而重构了多芯光纤的形状。Khan等^[6]分别在形状各异的模具中放入带有FBG传感器的螺旋芯和直芯，发现螺旋芯更适合扭曲的测量应用。杨濠琨^[7]采用FBG曲面重构算法对机器人触手形状进行了重构。张新华^[8]在基于正交曲率和Frenet方程的三维重构算法之上设计了基于FBG的无人机翼和蒙皮形变检测系统。Khan等^[9]利用Frenet框架，提出了一种基于四芯光纤的FBG传感器测量数据，重建医疗导管中心曲线的技术。傅程^[10]利用Frenet框架对光纤二维形状进行了还原。国内外研究现状主要集中在FBG传感器与二维层面，FBG传感器往往受限于环境变化的影响，而基于瑞利散射的OFDR光纤传感技术能带来更高的空间分辨率，实现全分布式监测^[11]。现有文献中尚未发现 OFDR传感器结合Frenet框架的三芯光纤三维重构的报道。

本文首先从理论上分析了光纤应变与光谱波长漂移量之间的物理关系，定义了三芯光纤表观曲率向量，推出曲率和挠率的计算公式，引入Frenet-Serret公式和插值拟合处理方法计算得出三维形状还原曲线的积分方程；接着利用ANSYS有限元仿真软件对S形应变数据进行建模并提取，代入算法并重建S形光纤；最后对重构误差进行分析并提出改进措施。

1 形状重构算法设计

1.1 理论基础

光频域反射技术通过测量传感量产生的相位改变，采用相位补偿思想，在解调后得到的光谱变化能反映应变、温度等传感量的变化程度^[12]。瑞利背向散射光谱的变化受应变与温度的影响可表示为

$ \frac{\Delta \lambda }{\lambda }=-\frac{\Delta \upsilon }{\upsilon }={k}_{\varepsilon }\varepsilon +{k}_{T}\Delta T $ (1)

式中： $ \Delta \lambda $为波长变化； $ \Delta \upsilon $为频率变化； $ \varepsilon $为应变大小； $ \Delta T $为温度变化； $ {k}_{\varepsilon } $和 $ {k}_{T} $分别为应变比例系数和温度比例系数。

要实现三维空间形状的测量，需要选取均匀分布的至少3根单模光纤或者三芯光纤对物体形状改变的应变进行测量^[13]。三芯光纤在弯曲时不容易受到损坏，具有较高的可靠性和可操作性，相比四芯或七芯光纤，三芯光纤更容易控制和操作，使得OFDR测量更加精准、高效。此外，三芯光纤的体积小、成本低，可以更轻松地安装在测量物体上，更好地满足大规模的测量需求。因此，本文选择三芯光纤作为研究对象。

在应变测量时，同一环境下温度基本保持不变，因此温度的变化往往可忽略。对 $ {k}_{\varepsilon } $进行标定之后，得到各个芯的频谱漂移量和应变的对应关系。随后采用合适的还原算法，对三维空间的光纤进行原始形态的还原。

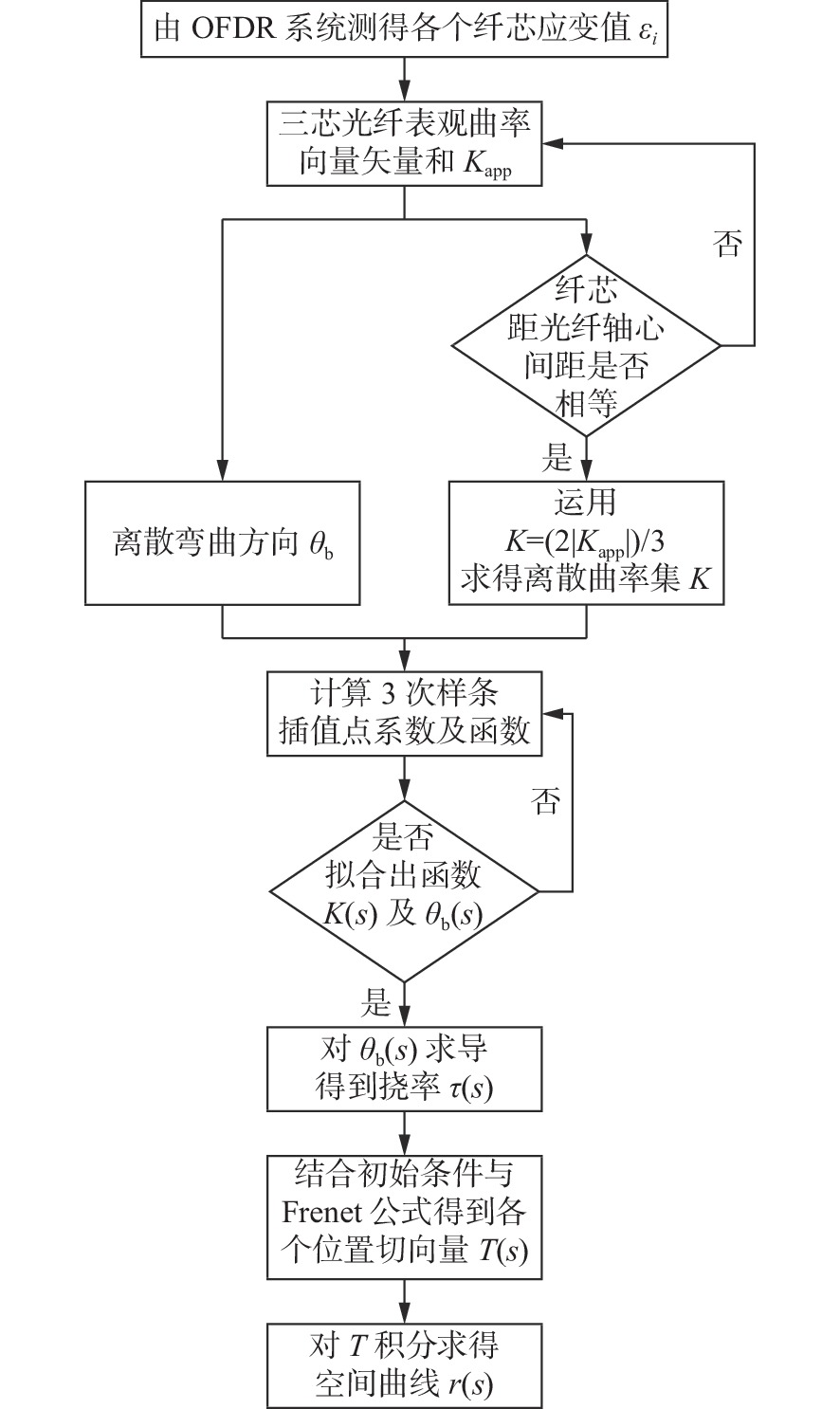
郭雅美^[14]提出了基于OFDR形状传感重构算法，本文在此基础上，加入样条插值拟合，具体流程如图1所示。

图 1. 重构算法流程图

Fig. 1. Flow chart of reconstruction algorithm

下载图片 查看所有图片

一般运用于形状传感的三芯光纤的截面图如图2所示。这里省略了涂覆层，光纤由纤芯、包层组成，纤芯之间以周向120°排布。 $ {\theta }_{i} $是局部坐标系的y轴正方向与第 $ i $个纤芯位置之间的角度， ${\theta }_{{\rm{b}}}$是局部坐标系中y轴与光纤弯曲方向之间的角度，r是纤芯与光纤几何中心之间的距离。

图 2. 三芯光纤截面图

Fig. 2. Cross section of three core fiber

下载图片 查看所有图片

单次应变测量往往会产生误差，因此利用来自所有芯的信息计算曲率。表观曲率向量定义为

$ {\boldsymbol{K}}_{{\rm{app}},i}\left(s\right)=-\frac{{\varepsilon }_{i}\left(s\right)}{{r}_{i}}\left(\mathrm{c}\mathrm{o}\mathrm{s}\;{\theta }_{i}\cdot \boldsymbol{j}+\mathrm{s}\mathrm{i}\mathrm{n}\;{\theta }_{i}\cdot \boldsymbol{k}\right) $ (2)

对于三芯光纤来说，曲率向量的向量和表达式为

$\begin{split} {\boldsymbol{K}}_{{\rm{app}}}\left(s\right)=& -{\sum }_{i=1}^{3}\frac{{\varepsilon }_{i}\left(s\right)}{{r}_{i}}\mathrm{c}\mathrm{o}\mathrm{s}\;{\theta }_{i}\cdot \boldsymbol{j}-\\ & {\sum} _{i=1}^{3}\frac{{\varepsilon }_{i}\left(s\right)}{{r}_{i}}\mathrm{s}\mathrm{i}\mathrm{n}\;{\theta }_{i}\cdot \boldsymbol{k} \end{split} $ (3)

式中： ${\boldsymbol{K}}_{{\rm{app}}}\left(s\right)$表示3根光纤在s处的总曲率向量； $ {\theta }_{i} $表示在s处第 $ i $个纤芯和局部坐标系y轴正方向之间的夹角； $ {r}_{i} $是第 $ i $个纤芯与光纤几何中心之间的距离；单位向量 $ \boldsymbol{j} $和 $ \boldsymbol{k} $对齐于 $ y $和 $ z $轴。

$ {\boldsymbol{K}}_{{\rm{app}},y}\left(s\right)=-{\sum }_{i=1}^{3}\frac{{\varepsilon }_{i}}{{r}_{i}}\mathrm{c}\mathrm{o}\mathrm{s}\;{\theta }_{i}\cdot \boldsymbol{j} $ (4)

$ {\boldsymbol{K}}_{{\rm{app}},z}\left(s\right)=-{\sum} _{i=1}^{3}\frac{{\varepsilon }_{i}}{{r}_{i}}\mathrm{s}\mathrm{i}\mathrm{n}\;{\theta }_{i}\cdot \boldsymbol{k} $ (5)

式中： ${\boldsymbol{K}}_{{\rm{app}},y}\left(s\right)$与 ${\boldsymbol{K}}_{{\rm{app}},z}\left(s\right)$分别为总曲率向量对应y，z轴的分量。

三芯光纤的弯曲曲率和弯曲方向由下式计算得出

$ k\left(s\right)=\frac{2|{\boldsymbol{K}}_{{\rm{app}}}(s)|}{3} $ (6)

$ {\theta }_{b}\left(s\right)=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left[\frac{{\boldsymbol{K}}_{{\rm{app}},z}\left(s\right)}{\left|{\boldsymbol{K}}_{{\rm{app}},y}\left(s\right)\right|}\right] $ (7)

将运用OFDR仪器测得的应变数据代入式（3），结合式（6）即可获得三芯光纤的弯曲曲率，将3个纤芯应变数据代入式（4）和式（5），再结合式（7）即可获得三芯光纤的弯曲方向^[15]。

对弯曲方向的连续函数求导即可得挠率随光纤长度变化的函数关系

$ \tau \left(s\right)={\theta' }_{b}\left(s\right) $ (8)

结合空间三维曲线的Frenet-Serret方程即可重构光纤形状，在三维弯曲条件下，三芯光纤几何中心曲线可以表示为弧长s（ $ 0\leqslant s\leqslant L $， $ L $是光纤总长度）的自然参数方程：

$ \boldsymbol{r}\left(s\right)=x\left(s\right)\boldsymbol{i}+y\left(s\right)\boldsymbol{j}+z\left(s\right)\boldsymbol{k} $ (9)

式中： $ \boldsymbol{i} $是 $ x $轴轴向单位向量； $ x\left(s\right)\mathrm{、}y\left(s\right) $和 $ z\left(s\right) $代表空间曲线的三维坐标； $ \boldsymbol{i},\boldsymbol{j} $和 $ \boldsymbol{k} $三者互相垂直正交。

1.2 Frenet-Serret框架

用来描述三维曲线运动轨迹的Frenet-Serret框架定义了曲线沿线各点的瞬时运动方向上的单位切向量T，垂直于切向量且指向弯曲中心的单位法向量N和单位副法向量B。此框架结合弹性杆理论和微分几何， T，N，B构成右手系。切线单位矢量对弧长的转动率即为弯曲曲率k（s）。挠率的绝对值是副法向量对于弧长的转动率，表示曲线扭曲，挠率为正时为右旋曲线；挠率为负时为左旋曲线；挠率为0时，曲线为平面曲线。

Frenet-Serret框架可以表示为

$ \left[\begin{array}{c}{\boldsymbol{T}'}\\ {\boldsymbol{N}'}\\ {\boldsymbol{B}'}\end{array}\right]=\left[-\begin{array}{ccc}0& k& 0\\ k& 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{c}{\boldsymbol{T}}\\ {\boldsymbol{N}}\\ {\boldsymbol{B}}\end{array}\right] $ (10)

$ \boldsymbol{T}\left(s\right)=\frac{{r'}\left(s\right)}{||{r'}\left(s\right)||}=\frac{\mathrm{d}r\left(s\right)}{\mathrm{d}s}={x'}\left(s\right)\boldsymbol{i}+{y'}\left(s\right)\boldsymbol{j}+{z'}\left(s\right)\boldsymbol{k} $ (11)

$\begin{split} \boldsymbol{N}\left(s\right)&= \frac{{T'}\left(s\right)}{||{T'}\left(s\right)||}\\ & =\frac{{x''}\left(s\right)\mathit{i} + {y''}\left(s\right)\mathit{j} + z''\left(s\right)\mathit{k}}{\sqrt{{\left({x''}\left(s\right)\right)}^{2} + {\left({y''}\left(s\right)\right)}^{2} + {\left({z''}\left(s\right)\right)}^{2}}} \end{split} $ (12)

$ \boldsymbol{B}\left(s\right)=\boldsymbol{T}\left(s\right)\times \boldsymbol{N}\left(s\right) $ (13)

将式（6）和式（8）代入框架，结合框架的方向初值以及曲线的位置初值 $ r\left(0\right) $即可重构出原三维曲线。一般情况下， $ r\left(0\right)=(\mathrm{0,0},0) $，所以曲线方程

$ r\left(s\right)=\int T\left(s\right){\mathrm{d}}_{s} $ (14)

1.3 插值拟合

由于本文仿真得到的应变数据是离散的，所以要选用合适的插值方法来构建曲率和弯曲方向的连续函数。吕安强等^[16]采用了3次样条插值的拟合方法，将光纤平均分为 $ n $段，已知光纤上n+1个点的应变和弯曲方向数据，这些点叫作样本点，即在光纤长度区间 $ [a,b] $上 $ n+1 $个分割点满足 $ a={s}_{0} ＜ {s}_{1} ＜ \cdots ＜ {s}_{n-1} ＜ {s}_{n} ＜ {s}_{n+1}=b $。

设 $ {s}_{j} $是光纤上某点与光纤初始点之间的长度，则在对应区间 $ [{s}_{j}，{s}_{j+1}] $（ $ j=\mathrm{1,2},\cdots ,n $）上，曲率和弯曲方向随着光纤长度变化的连续函数为

$ \begin{split} k\left(s\right)=&{a}_{j}\times {(s-{s}_{j})}^{3}+{b}_{j}\times {(s-{s}_{j})}^{2}+{c}_{j}\times\\ & \left(s-{s}_{j}\right)+{d}_{j} \end{split} $ (15)

$\begin{split} {\theta }_{b}\left(s\right)=&{e}_{j}\times {(s-{s}_{j})}^{3}+{f}_{j}\times {(s-{s}_{j})}^{2}+{g}_{j}\times\\ & \left(s-{s}_{j}\right)+{h}_{j} \end{split} $ (16)

式中： $ s $代表弯曲光纤的弧长； $ {a}_{j}，{b}_{j}，{c}_{j}，{d}_{j}，{e}_{j}， {f}_{j}，{g}_{j}和{h}_{j} $均为待定系数。

它们在各子区间 $ \left[{s}_{j}，{s}_{j+1}\right] $上为三次多项式。

2 分析与讨论

2.1 模型建立

本文利用Ansys workbench建立了三芯光纤有限元模型来验证算法的正确性，选取有利于提高计算精度的solid186单元，建立了如图3所示的简化几何模型，光纤总长为50 mm。三芯光纤材料的具体参数如表1所示。

图 3. 三芯光纤基础模型

Fig. 3. Three-core fiber model

下载图片 查看所有图片

2.2 重构分析

为了更好地展现出光纤的三维形变，本文设定的光纤变形情况为S形弯曲，从平面S形弯曲的基础上拓展到空间S形弯曲，分别测量出弯曲时的位移云图与轴向应变分布图，与应变分布的实际情况进行比较分析。最后将初始边界条件和纤芯弯曲数据代入相关公式，运用本文算法重构出三芯光纤的曲线方程。

首先在15 mm和35 mm处分别施加两个方向相反的1 mm位移载荷，使三芯光纤产生二维面上的S形弯曲，求解后得到的位移云图如图4所示。

图 4. 三芯光纤平面S弯曲位移云图

Fig. 4. Displacement cloud diagrams of three-core fiber after spatial planar S-bending

下载图片 查看所有图片

结合光纤长度分别提取3个纤芯的轴向应变值，绘制了平面S弯曲时3个纤芯的轴向应变分布曲线图，如图5所示。

图 5. 平面S形弯曲时三个纤芯的应变分布图

Fig. 5. Strain distribution of three fiber cores during planar S-shaped bending

下载图片 查看所有图片

拓展到三维空间，将原35 mm处所施加径向1 mm位移载荷转换到正交方向，其余条件不变，使三芯光纤产生空间S形弯曲，提取3个纤芯应变数据，通过本文算法重构光纤的形状。求解后得到的位移云图如图6所示。

图 6. 三芯光纤空间S弯曲位移云图

Fig. 6. Displacement cloud diagrams of three-core fiber after spatial S-bending

下载图片 查看所有图片

结合光纤长度分别提取3个纤芯的轴向应变值，绘制了空间S弯曲时3个纤芯的轴向应变分布曲线图，如图7所示。

图 7. 空间S形弯曲时三个纤芯的应变分布图

Fig. 7. Strain distribution of three fiber cores during spatial S-shaped bending

下载图片 查看所有图片

由图4、5可知，平面S弯曲时两端位移较小，弯曲部位位移最大，最大值为0.001 m左右，光纤上的位移分布与弯曲情况相符；纤芯2和纤芯3应变分布曲线几乎重叠，变化走势趋于一致，和纤芯1的变化趋势相反，在光纤的末端应变值趋于0。应变分布符合平面上S弯曲时纤芯的实际情况。

由图6、7可知，空间S弯曲时两端位移较小，弯曲部位位移最大，最大值为0.001 m左右，光纤上的位移分布与弯曲情况相符。纤芯1和纤芯2的轴向应变值趋势一致，和纤芯3相反，在光纤的末端应变值趋于0。应变分布符合空间S弯曲时纤芯的实际情况。

将初始边界条件和纤芯弯曲数据代入式（10）和式（14），即可重构出三芯光纤的曲线方程。三芯光纤的重构曲线方程可由初始边界条件和纤芯应变数据得到，对于光纤实际曲线，在ANSYS仿真软件的模型中间建立path，分别提取每个位置在x, y方向的变形得到。图8所示为光纤实际曲线对比重构曲线图，由图可知，该算法还原光纤三维形状的效果非常好。

图 8. 三芯光纤空间S形重构比较图

Fig. 8. Comparison of spatial S-shape reconstruction of three core fiber

下载图片 查看所有图片

2.3 误差分析

由于本文还原算法存在累计误差，通过末端位置误差和单位长度误差进行评价。位置误差公式为

$ {d}_{i}=\sqrt{{({x}'_{i}-{x}_{i})}^{2}+{({y}'_{i}-{y}_{i})}^{2}+{({z}'_{i}-{z}_{i})}^{2}} $ (17)

单位长度上的误差大小定义为

$ E=\frac{{d}_{i}}{{L}_{i}}\times 100 {\text{%}} $ (18)

并通过均方根误差（root mean square error, RMSE）进行分析，公式为

$ {\sigma }_{{\rm{RMSE}}}=\sqrt{\frac{\sum {\left(\right({x}'_{i}-{x}_{i})}^{2}+{({y}'_{i}-{y}_{i})}^{2}+{({z}'_{i}-{z}_{i})}^{2})}{n}} $ (19)

式中： $ {x}_{i}，{y}_{i}，{z}_{i} $代表光纤实际曲线坐标； $ {x}'_{i} $， $ {y}'_{i} $， $ {z}'_{i} $代表重构曲线的坐标； $ {L}_{i} $表示第 $ i $点与光纤起点之间的长度；d_i表示第 $ i $点处位置误差。对实际曲线和重构曲线按长度均匀提取50个坐标，代入式（17）、（18）、（19）进行计算，可得到光纤长度–位置误差曲线图，如图9所示。

图 9. 位置误差分布曲线图

Fig. 9. Distribution of position error

下载图片 查看所有图片

由图可见，位置误差随着光纤长度的增加逐渐增加，最大位置误差在末端。误差来源主要是对弯曲曲率和弯曲方向的样条插值误差以及Frenet框架还原会出现奇异点等问题。均方根误差计算结果为0.996 mm，计算得到单位长度误差最大值为0.0824%。

3 结　论

本文设计了基于Frenet-Serret框架的OFDR三维形状重构算法，并利用有限元仿真软件Ansys workbench建模S形弯曲时的三芯光纤，提取应变进行了算法验证。通过OFDR瑞利散射光谱波长漂移可以得到纤芯的应变分布数据，再结合本文的重构算法可以重构三芯光纤的形状。因为运用OFDR设备进行实验获取应变数据比较繁琐，本文直接利用有限元软件仿真三芯光纤三维形状的S形变化，并且得到每个纤芯的离散应变数据以及空间坐标系下的坐标数据。本文还原算法存在累积误差，即位置误差随着光纤长度的增加逐渐增加，误差来源主要是3次样条插值时产生的误差以及Frenet框架还原会出现奇异点等问题。均方根误差计算结果为0.996 mm，单位长度误差最大值为0.082 4%。未来将采用更高阶的样条插值方法，减小3次样条插值处理时带来的误差；在还原过程中将曲率限制在一个合理的范围内，从而有效避免还原时奇异点问题。本研究为更深入地研究OFDR形状检测提供了重要的理论基础，研究结果具有一定的工程应用价值。未来将以本研究为基础，进一步探讨减小算法累积误差的方法，探究长尺寸、大形变的光纤重建。