1. Introduction

Edge detection is one of the common data processing methods; and can resolve core problems in the field of machine vision, which has a wide range of applications in object detection^[1], image segmentation^[2], data compression^[3], microscopic imaging^[4], and object suggestion generation^[5]. Edges can be extracted by the spatial differentiator (SD) and reflect the key information in the image more efficiently^[6]. In the biomedical field, intensity changes of phase objects such as biological tissues and cells are usually weak^[7]. To more clearly and directly reflect the morphological boundary and structural characteristics of phase objects, it is of great significance to develop edge detection technologies for phase objects.

As a common method of phase imaging, differential interference contrast (DIC) technology can produce a relief effect for observing phase objects^[8,9]. However, the beam splitter prism can only be set in one direction to the image, and the relief effect only enhances the one-dimension edge. The differential interferometric imaging spectrometer can also record the phase information of the object, but the collected interference fringes need to be unwrapped to the image^[10]. To further detect the edge of the imaged object, the SDs need to be processed by digital or analog means.

Optical analog computing performs large-scale data processing at the speed of light and becomes a powerful tool to replace digital signal processing^[11,12]. For intensity objects, optical SDs based on surface plasmon polariton resonance^[13], the Brewster angle effect^[14], and anisotropic crystal birefringence^[15] were only effective for one-dimensional edge detection. The transfer function of nanophotonic material was regarded as a Laplacian operator to realize two-dimensional SD^[16]. However, due to the cross talk of incident light with different polarization directions, the edges with enough resolution were obtained only by working at the terahertz frequency. As for pure phase objects, the phase-contrast microscope based on Fourier optical spin splitting^[17] and quantitative phase gradient^[18] can only image one-dimensional edges and cannot avoid the anisotropy and artifact problems. In order to complete the isotropic two-dimensional edge detection, it is necessary to design the metasurface of the subwavelength structure and place it in the Fourier plane of a 4f system^[19,20]. The large 4f system is not conducive to structural design and limits the miniaturization of optical systems. Diffractive deep neural network (D2NN) is an all-optical neural network framework based on holographic technology and provides new ways to solve these problems^[21–23].

Here, we propose a diffractive neural network (differential interference contrast phase edging net, DPENet) based on the differential interference contrast principle to detect the edge of phase objects in an all-optical manner. In the simulation, the phase object is divided into incident light and reference light by dual Wollaston prisms (DWPs). Differential interference is accomplished by polarized light in the same direction by the polarizers. The diffractive neural network processes the original differential signal to obtain the edge image of the corresponding phase object. The scale of the edge can be changed by adjusting the air gap of the DWPs during detection. MNIST and NIST data sets were simulated to verify the performance of edge detection and generalization of the system. The F-score obtained on MNIST and NIST data sets is 0.9308 and 0.9352, respectively, and the highest imaging resolution can reach 420 nm. In addition, we also verified the application of DPENet in the field of biological imaging, which can detect the edge of biological cells and achieve the maximum F-score of 0.7462.

2. Principle

The structure of DPENet is shown in Fig. 1(a). DPENet is composed mainly of two parts. One part is an SD for the input phase object, and the other part is an all-optical D2NN processing module. The schematic diagram of integrating D2NN with a traditional DIC microscope for edge detection is shown in Fig. 1(b). In the DPENet, the DIC module is changed to SD for lensless imaging to reduce the size of the system.

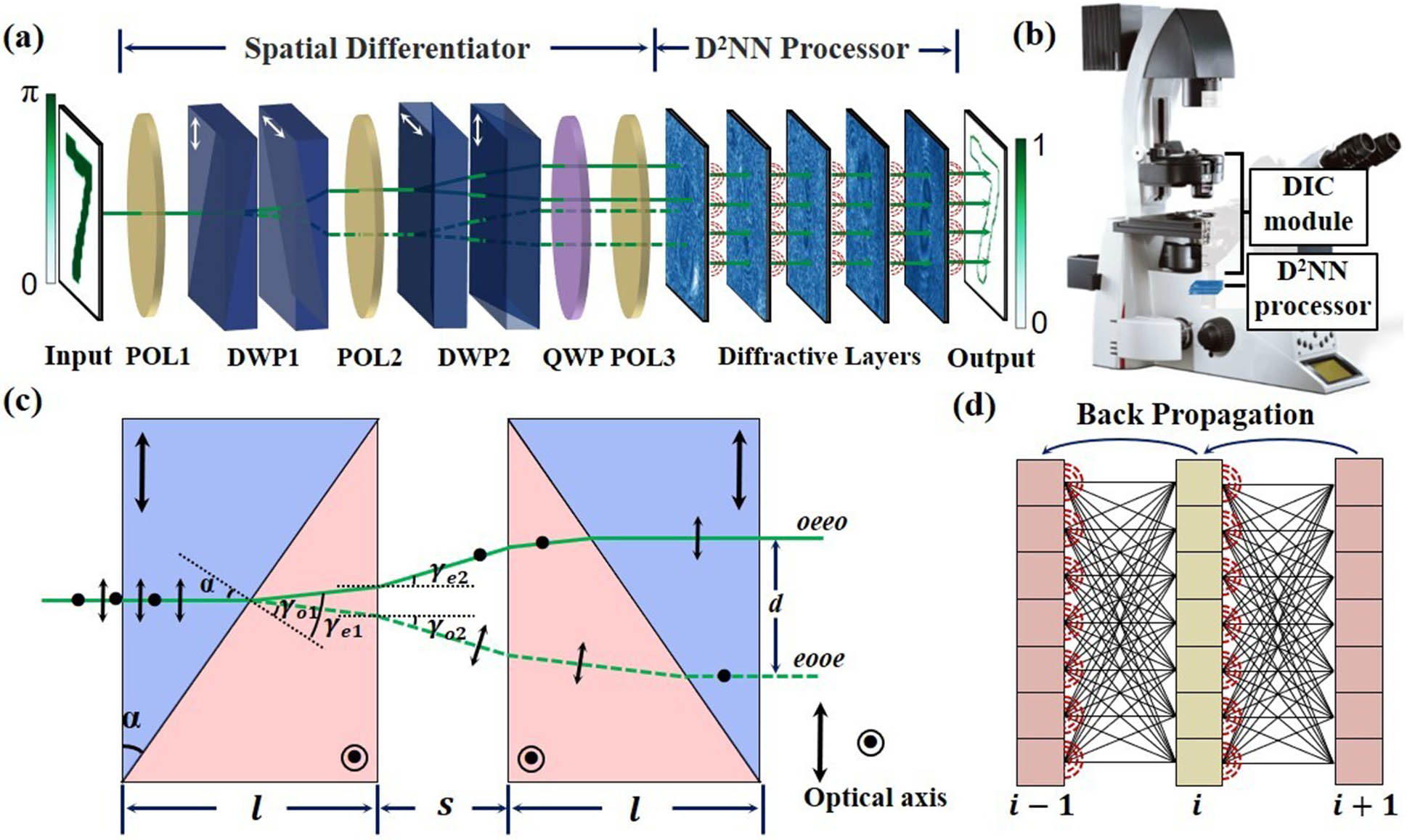
Fig. 1. (a) Schematic diagram of DPENet. The DPENet consists of two parts: spatial differentiator and all-optical processor. POL, polarizer; DWPs, dual Wollaston prisms; QWP, quarter-wave plate. (b) Edge detection system based on a DIC microscope. (c) Ray-tracing diagram of DWPs. α, structural angle of prisms; γ, refraction angle. (d) Schematic diagram of forward- and backpropagation of a three-layer D²NN.

下载图片 查看所有图片

In the SD part, the phase object is illuminated by coherent light. All polarizers are oriented at a 45° angle with respect to the horizontal direction. The polarized light is split into ordinary light and extraordinary light with perpendicular directions by DWPs. The ray-tracing diagram of the beam splitter that incorporates DWPs is illustrated in Fig. 1(c). Due to the birefringence property of the Wollaston prism, the ordinary light and extraordinary light are split into two parallel beams in the same direction as the incident light. The distance of splitting beams d can be expressed as^[24]d=ltan(γe1−α)+stanγe21−tanαtan(γe1−α)+ltan(α−γo1)+stanγo21+tanαtan(α−γo1),(1)where α is the structural angle of the Wollaston prism, γoi and γei, respectively, represent the refraction angles of ordinary light and extraordinary light at the ith interface, l is the thickness of the Wollaston prism, and s is the thickness of the air gap between the two prisms. These parameters except s are fixed parameters of the system, and they cannot be adjusted after the system is built. Therefore, to adjust the imaging scale of the edge in real time while the system is working, the scale of the spatial difference can be changed by adjusting the distance of the splitting beams. The resolution of the edge detection will be controllable. In the limit state with no gap, the differential dimension of space reaches the minimum. As the gap increases, the incident light and the reference light become more separated, resulting in thicker edges.

When the system is used as a one-dimensional (two-dimensional) differentiator, spatial difference can be accomplished by setting the DPWs in one (orthogonal) direction. Two orthogonally polarized lights are normalized to the uniform direction by the polarizer to produce interference, and the edge information will be encoded into the interference light field. The superimposed light field received by the detector can be expressed as^[25]$$\begin{gathered} Uout=|Aeiφ1+Aeiφ2+⋯+AeiφN|2 \\ =2A2∑i=1N∑j>iNcos(eiφi−eiφj)+A2N, \end{gathered}$$(2)where A is the amplitude of the input signals, φi is the phase of the input signal, and N is the number of input light channels.

The edge information will be enhanced and the overlapping part will be suppressed when the incident light and reference light with a phase difference are spatially differentiated. The total phase difference can be divided into the phase difference introduced by the DWPs and the quarter-wave plate. The phase difference of the DWP can be expressed as^[26]$$\begin{gathered} θDWP=2πλ((ne−no+nocos(γe1−α)−necos(α−γo1))l \\ +(1cosγe2−1cosγo2)s), \end{gathered}$$(3)where no and ne are the refractive indices of the birefringent crystal for ordinary light and extraordinary light, respectively.

The D2NN is used as an all-optical signal processor to modulate the phase and amplitude of the original differential signal and to obtain clear edges. The superimposed light field of the two beams contains the edge information corresponding to the separation distance, and the edge of the width equal to the separation distance can be extracted by the D2NN all-optical signal processor. A schematic diagram of forward- and backpropagation of a three-layer D2NN is demonstrated by Fig. 1(d). Each neuron is regarded as a new secondary wave source propagating by diffraction between layers. Its spatial diffractive propagation model is expressed by the Rayleigh–Sommerfeld diffraction equation in the far field^[27], wi(x,y,z)=z−zir2(12πr+1jλ)exp(j2πrλ),(4)where i represents the ith pixel of a given layer of the system located at position (xi,yi,zi), λ is the operative wavelength, r=(x−xi)2+(y−yi)2+(z−zi)2, and j=−1. The diffractive propagation of signal in optical differentiator is also defined by Eq. (4).

The ground truth of the edges for training and evaluation is obtained by the DexiNed model^[28]. The loss function is defined to evaluate the cross entropy (CE) between the intensity distribution of the outputs and the objects on the detection plane. The “Adam” optimization algorithm, which is adapted according to the optimization method based on stochastic gradient, is used to minimize the loss function. The network has a learning rate of 0.01 with a decay of 0.1 for every two epochs and a batch size of eight. It is implemented using Python version 3.7.11 and TensorFlow framework 1.15 (Google Inc.) and runs on a desktop computer (Nvidia Tesla T4 graphics processing unit, Intel Xeon Gold 5218 CPU, 16 cores, 256 GB RAM on Microsoft Windows 10).

3. Results and Discussion

The green laser with a wavelength of 532 nm is used as the input light source of DPENet. The pixel size is set to 420 nm, and the propagation distance between layers is 40λ. The output of the SD is discretized by the D2NN processor to a resolution of 200×200 to match the model.

Figure 2(a) compares the artificial neural network (ANN) (intensity input) and DPENet (complex light field input) of the same structure. The DPENet can directly process the complex light field to get the edge without an additional detector. However, the ANN with intensity input needs to detect the intensity before working, and the convergence effect is obviously worse than that of the complex light field input. In DPENet, the interference light field of spatially differential signal obtained by SD contains the edge information of the phase targets, and it needs to be processed to get a clear edge image by D2NN. Figures 2(b) and 2(c) show the processing flow of the interference light field emanating from the SD in a five-layer phase-only D2NN. It should be noted that D2NN directly processes complex light fields, and the figures only show the intensity distribution after each layer of processing.

Fig. 2. (a) Convergence plots of DPENet and ANN; (b) intensity of each layer of D²NN processor. The complex light field is directly phase-only modulated by D²NN, but only the intensity distribution of each layer is shown. (c) Phase parameters of each layer of D²NN obtained by training.

下载图片 查看所有图片

To demonstrate the edge detection capability of DPENet, the performance of the one-dimensional and two-dimensional edges was tested by using MNIST^[29] of 10 classes and NIST^[30] of 52 classes. The data set for the MNIST includes 60,000 data for training and another 10,000 for testing. The NIST data set contains 124,800 training data and 20,800 testing data, including 26 handwritten English letters in capital and lowercase letters. All results were simulated, and the same evaluation system including precision-recall (PR) curves and F-scores was adopted.

In Fig. 3(a), the one-dimensional and two-dimensional edges of the MNIST data set with perpendicular directions are displayed. The DPENet is highly sensitive to such tiny one-dimensional edges. It is observed that the edge is also detected in the tilt direction due to the resizing and discretization of the object, which causes the sloping edge to appear as a ladder shape in both horizontal and vertical directions. The F-score of the horizontal and vertical edges can reach 0.8966 and 0.9293, respectively. Figures 3(b)–3(e) show the results of two-dimensional edge detection of NIST by DPENet. The results show that DPENet can also directly perform two-dimensional edge detection of phase objects.

Fig. 3. (a) Perpendicular directions of edges of the MNIST; (b) and (c) are the partial results of capital letters; (d) and (e) are the partial results of lowercase letters; (f) PR curves of MNIST and NIST; the table shows the F-scores for the different testing data sets.

下载图片 查看所有图片

Moreover, DPENet can detect the two-dimensional edges with different resolutions, including thicker strokes (upside) and thinner strokes (downside). Figure 3(f) shows the PR curves of DPENet preforming the edge detection on MNIST and NIST. For MNIST and NIST edge imaging, the maximum F-score can achieve 0.9308 and 0.9352, respectively.

It is worth noting that since DPENet is a data-driven all-optical deep-learning paradigm, the large amount of training data makes the DPENet highly generalized.(1)The model trained on one data set can be directly applied for testing on an entirely new data set.(2)For the objects under the same category, different writing habits will have different shape, stroke thickness, tilt angle, etc. The model can carry out direct edge detection after training.(3)Model training only requires data at a single-edge scale, and testing for various edge scales can be accomplished by adjusting the air gap of the DWPs without additional training.

An additional data set was introduced to assess the edge detection performance of the network trained on the NIST data set using the resolution test charts. The results are shown in Fig. 4.

Fig. 4. (a) Results of edge detection for resolution test charts. Scale bars, 5 µm. (b)–(e) Edges under the splitting beams at a distance of 1, 2, 4, and 6 pixels, respectively; (f) resolution of edge imaging with different scales.

下载图片 查看所有图片

Figure 4(a) shows the simulation results of edge detection for the resolution test charts. For the area indicated by the red box, the edges under the splitting beams at the distance of 1, 2, 4, and 6 pixels are shown in Figs. 4(b)–4(e). To complete the edge detection with an adjustable scale, the distance of splitting beams can be changed by adjusting the air gap of the DWPs. This property is particularly significant when the size of the observed object is uncertain. A thick edge is not suitable for small objects, since it fails to reflect details, whereas a thin edge is not conducive to observing large objects due to the low contrast. Therefore, the scale of edge detection can be freely adjusted according to the target object. Notably, the scale of edges can be controlled by directly adjusting the gap without retraining the DPENet. Figure 4(f) shows the resolution with different scales of the same position in Figs. 4(b)–4(e) representing the full width of half-wave (approximately one to five pixels). Statistical analysis shows that DPENet can achieve a highest resolution of about 420 nm (single pixel).

Table 1 shows the comparison of different methods. The proposed method achieves 2D edge detection of phase objects with higher resolution through a more compact optical system.

With regard to dimensionality, the proposed method enables 2D edge extraction. Concerning the optical system, our approach avoids the need for a large 4f system; it only requires an SD module and D2NN for lensless imaging, facilitating instrument integration and miniaturization. In terms of resolution, we have achieved a finer edge imaging resolution of 0.42 µm compared with previous achievements.

To demonstrate the application of DPENet in edge detection of biological tissue, pathological section images from the National Cancer Institute GDC Data Portal^[31] consisting of 4500 training images and 1000 testing images have been used for simulation. Some measures were taken to extend the training data set to ensure the training effect, such as different directions of inversion and elastic deformation for data set^[32].

Figure 5 shows the edges of pathological sections. Unlike the DexiNed and the Canny operator^[33], DPENet can detect the edge of the phase object without staining cells and obtain results comparable to other detection results. As expected, the edges show the boundaries of the cell nucleus and reveal their shapes and positions. DPENet exhibits robust performance in achieving selective edge detection, even in the presence of substantial environmental noise during acquisition. As shown in Fig. 5(a), instances of ambient noise in the acquisition setting are correctly disregarded by DPENet, preventing misidentification as nuclei and enabling accurate edge detection. In Fig. 5(b), when the sample nucleus is compromised, distinct edge detection outcomes are generated by DexiNed and Canny operators, whereas DPENet consistently maintains stable detection results without succumbing to the impact. To quantitatively evaluate the results, the maximum F-score of 0.7462 could be reached.

Fig. 5. Results of edge extraction of pathological sections. (a) Environmental noise in the acquisition conditions; (b) the cell nucleus damage leads to detection confusion.

下载图片 查看所有图片

4. Conclusion

In conclusion, we proposed a scale-adjustable edge detection system, DPENet, for phase objects in an all-optical manner and simulated the optical SDs and the D2NN. DPENet can detect the edge information of phase targets by interference difference and uses passive diffractive layers as an optical processing device to ensure the high-speed operation and transmission efficiency of edge detection. No lens or imaging system is used in the whole system, which successfully reduces the complexity of the device. Compared with the ANNs, our proposed system does not need to collect the intensity distribution in advance, but directly modulates the complex light field to enable real-time online edge detection of phase objects.

At present, there have been many successful end-to-end cases of phase object imaging through high-performance models in the field of electrical neural networks^[33–37]. The cascaded D2NN is only completed by the integral transfer of phase-modulated layers and diffraction between layers, and it is still a linear system in nature^[21]. Many researchers have proposed improved models for a cascaded D2NN model, which is expected to greatly improve the computing power of the model^[38,39]. There are also many studies on optical nonlinear activation proposed to increase the nonlinear fitting ability of D2NN networks to further improve computing power^[40]. We believe that with the strong advancement of the high-performance D2NN model and nonlinear activation research, it is expected to form end-to-end real-time edge detection for phase objects.