光量子精密测量研究进展（特邀）

王犇; 张利剑

doi:doi:10.3788/CJL231494

中国激光, 2024, 51 (1): 0112001, 网络出版: 2024-01-24

光量子精密测量研究进展（特邀）下载： 781次创刊五十周年特邀

Progress in Photonics Quantum Metrology (Invited)

论文大纲

王犇 ^1,2,3,4张利剑 ^1,2,3,4,*

作者单位

¹ 南京大学现代工程与应用科学学院，江苏南京 210023

² 智能光传感与调控技术教育部重点实验室，江苏南京 210023

³ 人工微结构科学与技术协同创新中心，江苏南京 210023

⁴ 南京大学固体微结构物理国家重点实验室，江苏南京 210023

量子光学量子精密测量参数估计海森堡极限传感 quantum optics quantum metrology parameter estimation Heisenberg limit sensing

AI 词云图 AI一句话精读 AI短摘要

注：本部分内容由 AI 自动生成，请您知悉。

摘要

量子精密测量作为当代量子力学的主要应用方面之一，近些年来一直是量子科技的重要研究和发展方向。量子精密测量的主要研究目标是针对物理系统中的未知参数，利用量子资源进行量子增强测量，以提升参数测量精度。与其他物理系统相比，光子系统具有相干时间长、不易受到环境干扰等优越性，因而常被用作量子信息处理的载体。以光子为基础的传感器提升传感精度是光量子精密测量的主要任务。介绍了量子精密测量的一般性原理，给出参数估计的量子极限精度下界。同时，介绍了目前光量子精密测量的理论与实验研究进展以及相应的挑战。

Abstract

Significance

Quantum metrology, as one of the primary applications of contemporary quantum mechanics, has emerged as a crucial area of research in quantum technology in recent years. The fundamental objective of quantum metrology is to utilize quantum resources to enhance the precision of measuring unknown parameters in physical systems. Compared with other physical systems, photon-based systems possess distinct advantages such as long coherence time and low interaction with the environment, making them an ideal platform for processing quantum information. Improving sensing precision through photon-based sensors stands as a pivotal task within optical quantum metrology.

Progress

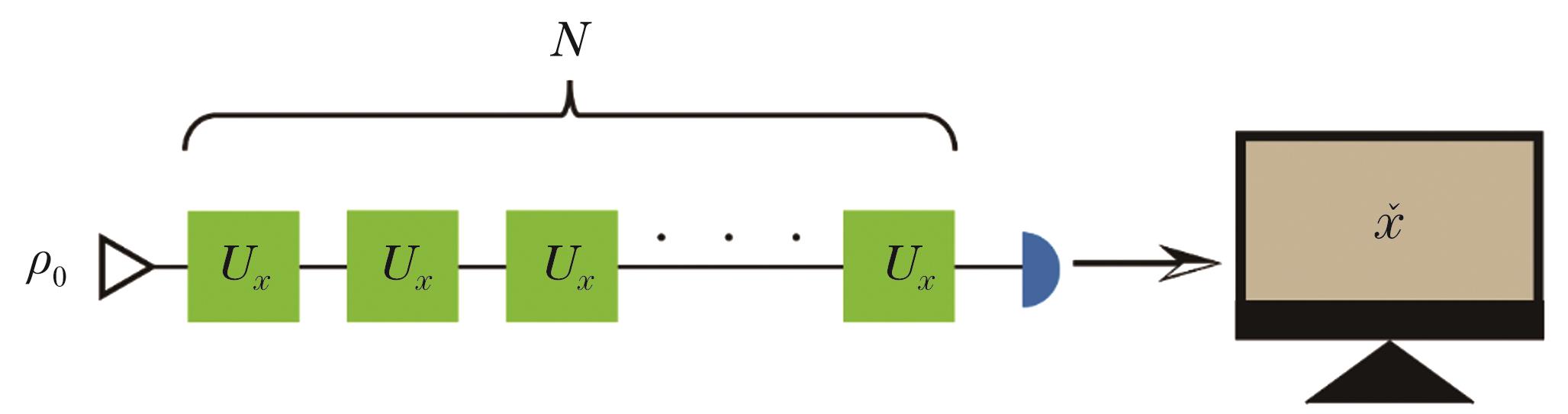
The general process of quantum metrology can be abstracted into four steps 1) preparation of a probe state; 2) interaction of the probe with the system to be measured; 3) measurement; 4) classical estimation, as shown in the main text (Fig.1). In terms of unitary evolution, Lloyd et al. compared the precision bound provided by four strategies, i.e., classical-classical (CC) strategy, classical-quantum (CQ) strategy, quantum-classical (QC) strategy and quantum-quantum (QQ) strategy (Fig.2). The QC and QQ strategies provide the ultimate precision of parameter estimation beyond the CQ and CC strategies. By analyzing the different strategies, one can easily find the relationships among the Fisher information, the QFI, the SQL and the HL (Table 1).

The fundamental theory of quantum metrology is based on the principles of parameter estimation theory. The quantum Cramér-Rao bound (QCRB) serves as a widely utilized mathematical tool in quantum metrology for evaluating the ultimate limit of precision. In the context of single parameter estimation, it is inversely proportional to the quantum Fisher information (QFI). By scrutinizing the QFI associated with different quantum states encoding parameters, one can determine which type of quantum states would be the most optimal for a given sensing task involving an unknown parameter.

The optical interferometer is a crucial apparatus in optics and plays an indispensable role in quantum metrology. Its applications range widely, from spectroscopic interferometric techniques to remarkable examples involving stellar interferometry and gravitational wave detection. Classical theory does not provide precise analysis of phase shift estimation in the interferometer, while the semi-classical theory, considering the quantized detection process, establishes the shot noise limit or standard quantum limit (SQL) of precision with N detected photons. However, it should be noted that SQL should not be considered as the fundamental bound when non-classical states of light, such as squeezed states, are injected into the interferometer. The maximally entangled photon number state known as NOON state can achieve a precision of 1/N referred to as the Heisenberg limit (HL). In comparison with SQL, HL exhibits scaling improvement and represents the fundamental bound for parameter estimation. Quantum resources like squeezing and entanglement can genuinely enhance phase estimation precision, while employing a sequential strategy where probe states undergo a sequential process can also yield maximal precision.

In recent years, quantum metrology has experienced rapid development, witnessing the generation of numerous non-classical quantum states with inherent metrological advantages and the invention of various interferometer structures aimed at enhancing phase estimation precision. Consequently, it is imperative to comprehensively and meticulously summarize existing research in order to provide guidance for future advancements in this field.

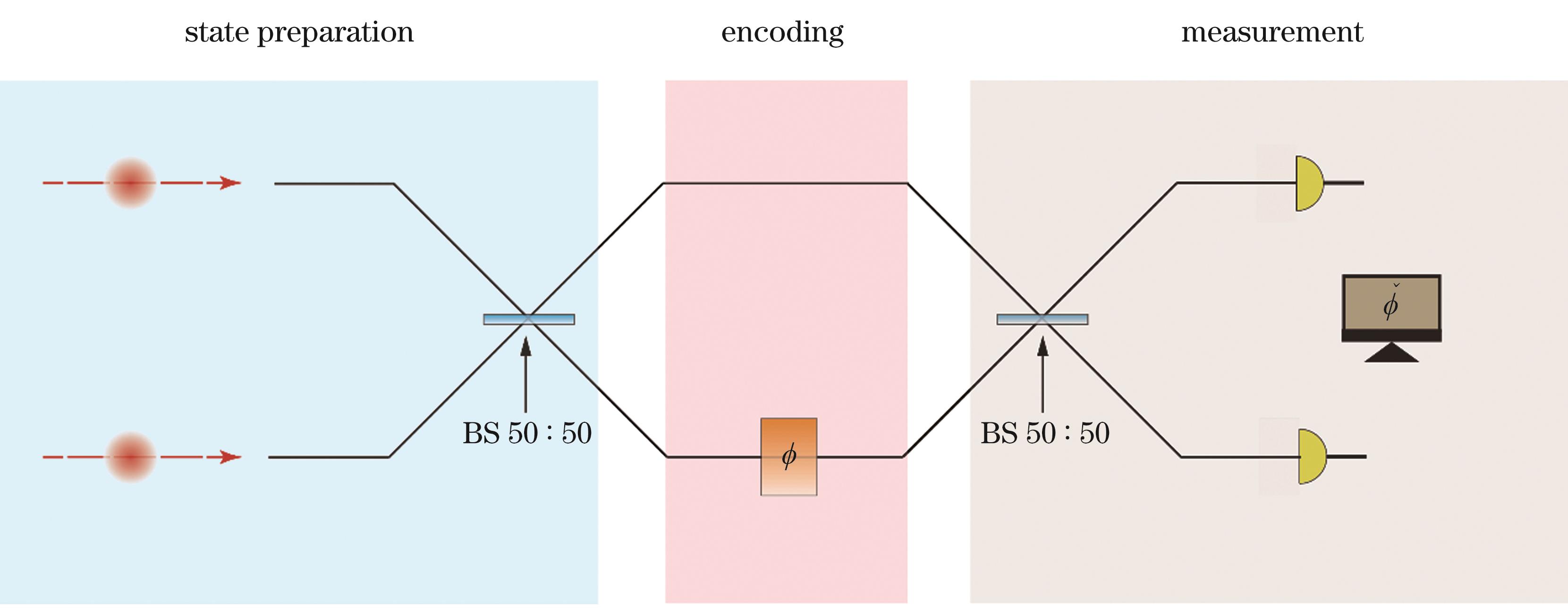
The fundamental principles of quantum metrology are elucidated, albeit in an abstract manner. To provide a more concrete illustration, we will consider the phase estimation problem as a prime example, which represents the most captivating application within quantum metrology. The Mach-Zehnder interferometer (MZI) serves as the prevailing structure (Fig.4). Numerous studies propose that by introducing distinct non-classical quantum states such as squeezed states and NOON states into the MZI, it is possible to enhance the estimation precision of phase shift in its two arms. Other types of interferometers like Michelson interferometer and Sagnac interferometer (Fig.6) also play significant roles in gravitational wave detection and quantum gyroscope applications. In practical scenarios, noise inevitably exists within interferometers. For instance, losses are almost unavoidable and can compromise precision levels. This review introduces several approaches aimed at mitigating the impact of loss.

In most realistic sensing scenarios, the system to be measured typically encompasses multiple unknown parameters. Multiparameter quantum metrology is also a crucial research aspect within the field of quantum information science, encompassing tasks such as estimating multiple phases, distributed quantum sensing, phase and phase diffusion, and so on. Besides addressing the phase estimation problem, optical quantum metrology finds numerous other applications including imaging and magnetometer. Finally, we provide a brief overview of some relevant works.

Conclusions and Prospects

Photon, as an excellent information carrier, is suitable to be applied in quantum metrology, thereby establishing optical quantum metrology as a pivotal and burgeoning field of research. Further comprehensive and meticulous investigations are imperative to advance the theoretical and experimental development of optical quantum sensing. This review gives an in-depth and detailed introduction of recent progress in optical quantum process and we hope it will inspire some interest of readers.

1　引言

测量是人类从自然界获取信息的手段，而物理学的突破和发展源于对自然界更为细致的测量与观察。作为目前最完备的物理学基础理论体系之一，量子力学在微观尺度下对物体行为的研究无疑是成功的。因此，利用量子力学基本原理，对测量这一物理过程进行更为基础且全面的分析，不仅可以为基础理论科学的发展打下基础，而且更有利于发展新的量子科技并使其应用于实际工程中。

以提高测量精度为目标的量子精密测量技术作为当代量子信息技术的重要研究方向，一直受到广泛的关注。量子精密测量利用量子资源，如纠缠、压缩等，提升对物理量的测量精度，因而有望为基础科学研究（如基本物理常数的测量）以及实际工程应用（如导航定位、资源勘探）带来变革性突破。在过去几十年中，量子精密测量技术取得了长足的进步，相关研究人员发展了各种基于量子干涉仪^［1-4］、非线性^［5-6］、弱测量^［7-8］等物理系统和量子效应的新型测量方案。实验方面也不断突破，一些量子传感方案已经在光子、原子、核磁共振及固态系统中成功演示，并在引力波探测^［9-10］、潜艇导航等方面获得应用。

相比于固体系统与原子系统^［11-12］，光子具有相干时间长、不易受干扰、易于调控等特性，因此光子系统针对精密测量任务具有天然优势而得到更好的发展。由于多数传感与测量任务都可以等效为光学相位的测量，因此，光量子精密测量的一类重要任务就是针对相位参数进行测量与估计。本综述聚焦于光量子精密测量的各个方面的理论与实验研究，对现有的光量子精密测量研究进展进行总结概括。

本文首先介绍了量子精密测量的基本原理，以量子力学的语言描述精密测量的一般过程，并介绍了量子资源如纠缠和压缩等在精密测量中的应用，接下来主要介绍光量子精密测量的具体应用，包括量子资源在光学干涉仪中针对相位测量的应用，同时也介绍了光量子精密测量在其他一些方面的应用，最后对全文进行总结。

2　量子精密测量的基本原理

2.1　量子精密测量的一般过程

如图1所示，量子精密测量的基本过程由4个步骤组成^［13］：1）用于感知未知参数探测态 $ρ_{0}$ 的制备。2）将探测态与待测系统相互作用，该过程可以用一般的量子过程 $Γ_{x} (ρ_{0})$ 描述，其中x为待测的位置参数，因而相互作用后探测量子态变为 $ρ_{x} = Γ_{x} (ρ_{0})$ 。若该量子过程为幺正演化过程，则 $ρ_{x} = U_{x} ρ_{0} U_{x}^{†}$ 。3）针对 $ρ_{x}$ 进行测量来提取参数信息。任何量子测量可以由一组正算子值测量（POVM）算符 ${{\hat{E}}_{i}}$ 来描述。4）根据测量结果选择合适的经典估计算法提取出待测系统中的参数信息。

图 1. 量子精密测量的一般过程

Fig. 1. General process of quantum metrology

下载图片查看所有图片

一般情况下，以多次测量的估计值的方差 $Δ^{2} x$ 衡量参数测量精度。因此，由经典概率论中的中心极限定理可知，当重复进行实验时，随着入射量子态个数N的增加，估计的标准差会以 $\sqrt[]{N}$ 的比例降低，这也被称为标准量子极限（SQL）或散粒噪声极限（SNL）。SQL是经典力学可以达到的最终测量精度极限，而量子力学中的海森堡不确定性关系则给定了物理量测量的最终量子极限精度即海森堡极限（HL） $Δ x ~ 1 / N$ 。达到HL需要入射的N个量子态存在非经典的关联，如量子纠缠。因此，利用量子资源可以突破经典极限的限制，精度会有 $\sqrt[]{N}$ 倍的提升。

2.2　量子参数估计理论

量子精密测量的理论基础是量子参数估计理论。给定含参量子态 $ρ_{x}$ 与一组POVM ${{\hat{E}}_{i}}$ ，得到测量结果为i的概率为 $p (i | x) = T r (ρ_{x} {\hat{E}}_{i})$ 。当重复 $ν$ 次实验时，可以得到一组测量结果 ${i_{1}, i_{2}, \dots, i_{ν}}$ ，从该组测量结果可以对未知参数x进行“猜测”： $\tilde{x} ({i_{k}})$ 。这种“猜测”是将测量结果 ${i_{k}}$ 与推断结果 $\tilde{x}$ 建立对应关系的函数，称之为估计子。衡量该估计子性能的关键指标有两个：偏差 $E [\tilde{x} - x]$ 与方差 $E [(\tilde{x} - E {[\tilde{x}])}^{2}]$ ，其中 $E [\cdot]$ 是针对所有测量结果求期望。偏差 $E [\tilde{x} - x]$ 衡量了估计子的准确度，一般来说需要选择无偏估计子，即 $E [\tilde{x} - x] = 0$ ，而方差 $E [(\tilde{x} - E {[\tilde{x}])}^{2}]$ 则衡量估计的精度。对于无偏估计来说，均方误差（MSE）定义为

e_{M S E} (x) = \sum_{i} {[\tilde{x} (i) - x]}^{2} p (i | x)

，（1）

其值与方差相同。在经典参数估计理论中，针对单一参数x，参数估计的方差 $Δ^{2} x$ 存在理论的下界，该下界由Cramér-Rao不等式给出：

Δ^{2} x \geq \frac{1}{ν F_{x}}

，（2）

式中： $F_{x}$ 为Fisher信息。Fisher信息衡量了测量过程中针对未知参数可以获得的信息量大小，其定义为

F_{x} = \sum_{i} \frac{1}{p (i | x)} {[\frac{\partial p (i | x)}{\partial x}]}^{2}

。（3）

若想达到由Fisher信息所决定的精度，则需要选择合适的估计方法，如最大似然估计、贝叶斯估计等。上述经典参数估计理论仅仅关注图1过程中的最后一步，即选择合适的估计子。然而，量子态 $ρ_{x}$ 中参数x的最终测量精度是由量子态决定的，而不依赖于测量方式，因此有

Δ^{2} x \geq \frac{1}{ν F_{x}} \geq \frac{1}{ν Q_{x}}

，（4）

式中： $Q_{x}$ 为量子Fisher信息，定义为

Q_{x} = T r [ρ_{x} {\hat{L}}_{x}^{2}]

，（5）

式中： ${\hat{L}}_{x}$ 为对称对数导数（SLD），满足 $\partial_{x} ρ_{x} = ({\hat{L}}_{x} ρ_{x} + ρ_{x} {\hat{L}}_{x}) / 2$ 。

若将量子态 $ρ_{x}$ 进行谱分解 $ρ_{x} = \sum_{i} λ_{i} | ψ_{i}〉〈ψ_{i} |$ ，则量子Fisher信息可以由下式计算得到：〈〉

Q_{x} = \sum_{i} \frac{(\partial_{x} λ_{i})^{2}}{λ_{i}} + 2 \sum_{i \neq j} \frac{(λ_{i} - λ_{j})^{2}}{λ_{i} + λ_{j}} | 〈ψ_{i} | \partial_{x} ψ_{j}〉 |^{2}

。（6）

如果量子态为纯态，记为|ψ_x〉，则量子Fisher信息的计算可以简化为

Q_{x} = 4 (〈\partial_{x} ψ_{x} | \partial_{x} ψ_{x}〉 - | 〈\partial_{x} ψ_{x} | ψ_{x}〉 |^{2})

。（7）

除了上述定义，量子Fisher信息的计算还有众多其余形式，详见文献［14］。

方差、Fisher信息与量子Fisher信息三者的关系可以由下述优化关系描述：

F_{x} = m a x_{\tilde{x}} \frac{1}{ν Δ^{2} x}, Q_{x} = m a x_{{{\hat{E}}_{i}}} F_{x}

。（8）

因此，若想达到量子Fisher信息所给定的精度极限，就需要寻找到最优测量方案，使得对应的经典Fisher信息与量子Fisher信息相等。由量子Fisher信息的定义，最优测量实际包含在SLD算符中，对参数x的最优测量方案是SLD的本征态组成的一组投影测量^［15］，然而该组最优测量往往依赖于参数的真实值，因此需要通过自适应的方式渐进地达到量子极限精度^［16-18］。

与经典Fisher信息类似，量子Fisher信息具有重要的性质：

1）凸性， $Q_{x} (\sum_{n} p_{n} ρ_{n}) \leq \sum_{n} p_{n} Q_{x} (ρ_{n})$ ，其中 $p_{n} > 0, \sum_{n} p_{n} = 1$ 。

2）可加性， $Q_{x} (\otimes_{n} ρ_{n}) = \sum_{n} Q_{x} (ρ_{n})$ 。

上述针对量子Fisher信息的分析主要集中于针对参数编码后的末态 $ρ_{x}$ 进行最优测量以提升参数估计精度，该过程仅仅利用到量子化语言以描述该寻找最优测量的方法，而并未完全体现其量子优势。接下来我们将集中讨论利用量子资源突破经典参数估计精度极限。

2.3　基于量子资源的量子增强精密测量

上述讨论主要集中于寻找针对末态的最优测量，而由量子精密测量的一般过程可以得知，通过优化入射的初态 $ρ_{0}$ ，我们可以得到相应的最大化的量子Fisher信息。而如何针对特定的量子过程与参数决定最优入射态也是量子精密测量的重要研究方向。此处，我们首先考虑幺正的演化过程 $U_{x} = e x p (- i \hat{H} x)$ ，其中 $\hat{H}$ 为厄米算符（也称之为参数x的产生算符）。考虑到入射态为 $ρ_{0}$ ，则末态为 $ρ_{x} = U_{x} ρ_{0} U_{x}^{†}$ 。入射态为纯态时，该演化过程为 $| ψ_{x}〉 = U_{x} | ψ_{0}〉$ ，则 $\partial_{x} | ψ_{x}〉 = - i \hat{H} U_{x} | ψ_{0}〉$ 。根据式（7），可以得到此时的量子Fisher信息为

Q_{x} = 4 (〈ψ_{0} | {\hat{H}}^{2} | ψ_{0}〉 - {〈ψ_{0} | \hat{H} | ψ_{0}〉}^{2}) = 4 Δ^{2} H

。（9）

若希望达到最大的量子Fisher信息，就需要寻找到针对厄米算符 $\hat{H}$ 最大测量方差的态。针对该算符，其测量方差最大的态为其最大本征值对应的本征态与最小本征值对应的本征态的叠加^［19-20］：

| ψ_{m a x}〉 = \frac{| h_{m i n}〉 + | h_{m a x}〉}{\sqrt[]{2}}

。（10）

此时对应的量子Fisher信息为 $h_{m a x} - h_{m i n}$ ，其中 $| h_{m a x}〉$ 为最大本征值 $h_{m a x}$ 所对应的本征态， $| h_{m i n}〉$ 为最小本征值 $h_{m i n}$ 所对应的本征态。若制备N个 $| ψ_{m a x}〉$ ，则对参数x的测量最大精度为 $Δ x = 1 / \sqrt[]{ν N} (h_{m a x} - h_{m i n})$ ，此时针对参数x的估计精度依然是SQL，

| ψ_{e n t}〉 = \frac{| {h_{m i n}〉}^{\otimes N} + | {h_{m a x}〉}^{\otimes N}}{\sqrt[]{2}}

。（11）

该量子态的量子Fisher信息为 $N^{2} (h_{m a x} - h_{m i n})^{2}$ ，因此对参数x测量的标准差下界为 $1 / N (h_{m a x} - h_{m i n})$ 。该测量精度已经超越SQL达到HL。图2（d）代表态制备与测量端都包含量子资源即量子-量子方案（QQ），Giovannetti等^［19］证明，QQ方案并不会提供超越QC方案的精度。综上所述，联合测量方案对于单参数量子精密测量来说并不会提供超越局域测量的精度，但该方案在多参数情形下有所不同^［26］，区别将在后文介绍。

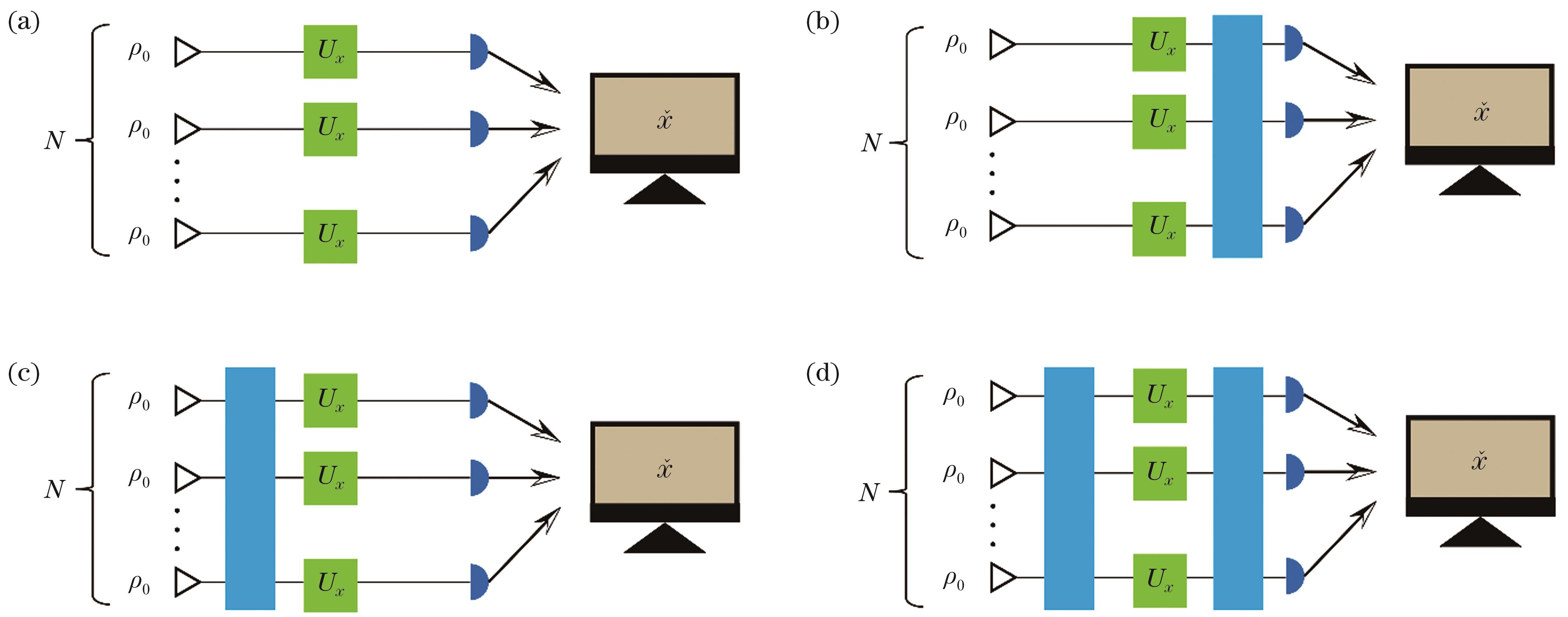
图 2. 针对未知参数测量的4种不同的并行方案。（a）经典-经典方案；（b）经典-量子方案；（c）量子-经典方案；（d）量子-量子方案

Fig. 2. Four different parallel strategies for estimation of unknown parameter. (a) Classical-classical strategy; (b) classical-quantum strategy; (c) quantum-classical strategy; (d) quantum-quantum strategy

下载图片查看所有图片

均方差、Fisher信息、量子Fisher信息、SQL与HL之间的相互关系由表1给出^［13］。

表 1. 五种关键指标的相互关系

Table 1. Interrelationship of five key quantities

Quantity	Initial $ρ_{0}$	POVM	Estimator
e_MSE（x）	Fixed	Fixed	Fixed
$F_{x}$	Fixed	Fixed	Optimized
$Q_{x}$	Fixed	Optimized	Optimized
SQL	Classically optimized	Optimized	Optimized
HL	Quantum optimized	Optimized	Optimized

查看所有表

MSE作为衡量参数估计精度的指标，是由得到的测量数据决定的。因此当固定了入射态、测量方式以及估计子后，MSE也就随之确定。而Fisher信息则决定了选取最优的估计子后MSE能达到的最优精度。如表1中所示，当入射量子态与测量方式固定时，采用何种估计方式（最小二乘法、最大似然法、贝叶斯等）会影响MSE的大小，这其中最优的估计方法决定了最小的MSE，而该最小的MSE则与Fisher信息直接相关。量子Fisher信息直接由量子态决定，即当量子态固定时，通过选择最优的测量方案与最优估计方法所决定的最高精度。SQL考虑了对量子态作经典优化，即各个量子态之间不存在量子关联，此时对应的量子Fisher信息则为SQL。HL则是对于入射态也进行量子最优化处理，允许入射态是纠缠的。

图2对应的方案都是并行方案（PS），即N个入射态平行入射，同时经历该幺正过程 $U_{x}$ 。为了便于描述，我们此处将式（11）中 $| h_{m i n}〉 \to | 0〉, | h_{m a x}〉 \to | 1〉$ 。因此式（11）在耦合参数后会变为

\frac{| {0〉}^{\otimes N} + e x p [- i N (h_{m a x} - h_{m i n}) x] | {1〉}^{\otimes N}}{\sqrt[]{2}}

。（12）

对参数测量精度达到HL的数学本质在于对参数x“折叠”了N次，即若 $Δ^{2} N x \geq 1$ ，则 $Δ^{2} x \geq 1 / N^{2}$ 。类似地，可以使单个入射态通过N次相同的量子过程以达到相同的效果，即串行方案（SS）^［27-30］，如图3所示。

图 3. 串行方案

Fig. 3. Sequential strategy

下载图片查看所有图片

如图3所示，入射态 $(| 0〉 + | 1〉) / \sqrt[]{2}$ 通过N次 $U_{x}$ 后，末态变为

\frac{| 0〉 + e x p [- i N x (h_{m a x} - h_{m i n})] | 1〉}{\sqrt[]{2}}

，（13）

其量子Fisher信息也达到了HL。

上述分析主要针对耦合过程为幺正演化的情形。对于非幺正演化的一般过程，如完全正定保迹量子过程（CPTP），耦合可以用一组Kraus算子来表示：

ρ_{x} = \sum_{i} {\hat{K}}_{i} (x) ρ_{0} {\hat{K}}^{†} (x)

，（14）

式中： $\sum_{i} {\hat{K}}^{†} {\hat{K}}_{i} = I$ 。

Escher等^［31］指出，在参数耦合过程中，某些类型的噪声，如退相干、损耗等，会使参数估计的精度无法达到HL^［32］，即便选择最优的纠缠态入射。在此基础上，Demkowicz-Dobrzański等^［33］基于量子信道的几何结构与半正定算法，推导出了相应噪声下可以达到的量子极限。

3　光量子精密测量及其应用

量子信息技术可以由各种物理系统实现，其中光子系统是应用最为广泛的物理系统之一^［34-36］。光子具有相干时间长、不易受干扰、易于调控等性质，因而常被作为量子信息处理的基本单元，例如利用非线性过程——自发参量下转换（SPDC）产生纠缠光子对^［37］或压缩态^［38］等非经典光学量子态完成各类量子信息处理任务，如量子隐形传态等^［39-40］。此外，光子的不同自由度可以用于编码或者提取信息，如光子的偏振、路径、时间、轨道角动量等。现代光学发展的针对光子的产生、操纵和探测技术使得我们对光子不同自由度对应的量子态的信息处理成为可能^［41-42］。

3.1　光学干涉仪

量子精密测量在光学领域最常见的应用是光学干涉仪。光学干涉仪由于其针对相位的测量精度能达到亚波长的测量精度，从宇宙学（引力波探测）^［9］到显微成像（相衬显微成像）^［43-53］等各种领域都有广泛应用。Mach-Zehnder干涉仪（MZI）的一般结构如图4所示，在两个入射端口入射两个光场量子态进入分束器（BS），出射的两路光其中之一感知未知相位 $ϕ$ ，而后两路光同时进入另一个BS中，针对出射两个端口进行测量并根据测量结果估计未知相位。

图 4. Mach-Zehnder干涉仪的一般结构

Fig. 4. General construction of Mach-Zehnder interferometer

下载图片查看所有图片

MZI的结构于19世纪90年代首次提出，其量子描述于1986年由Yurke等^［4］首次给出。MZI中的BS与加载相位的过程都可以用幺正演化来描述，其中BS的数学形式为 $B = e x p (- i π {\hat{J}}_{x} / 2)$ ，其中 ${\hat{J}}_{x} = ({\hat{a}}^{†} \hat{b} + {\hat{b}}^{†} \hat{a}) / 2$ 。 ${\hat{J}}_{x}$ 中包含两个端口输入光场的产生与湮灭算符，其中上路径的产生（湮灭）算符记为 ${\hat{a}}^{†}$ （ $\hat{a}$ ），相应的下路径的产生（湮灭）算符为 ${\hat{b}}^{†}$ （ $\hat{b}$ ）。在下路径上附加未知相位的操作记为

U = e x p (- i \frac{{\hat{a}}^{†} \hat{a} - {\hat{b}}^{†} \hat{b}}{2} ϕ) = e x p (- i {\hat{J}}_{z} f)

。（15）

而后再经过另一个50∶50的BS后，光子进入探测器测量。MZI的整体过程可以由下式描述：

I (ϕ) = B U (ϕ) B^{†} = e x p (- i {\hat{J}}_{y} ϕ)

，（16）

式中： ${\hat{J}}_{y} = ({\hat{a}}^{†} \hat{b} - {\hat{b}}^{†} \hat{a}) / (2 i)$ 。

此时，经过态制备与编码未知相位过程后的量子态 $| ψ_{ϕ}〉$ 的量子Fisher信息可由式（9）推出：

Q_{f} = 4 (〈ψ_{ϕ} | {\hat{J}}_{z}^{2} | ψ_{ϕ}〉 - {〈ψ_{ϕ} | {\hat{J}}_{z} | ψ_{ϕ}〉}^{2}) = 4 Δ^{2} {\hat{J}}_{z}

。（17）

3.2　光学干涉仪中的标准量子极限与海森堡极限

在利用上述MZI进行相位测量时，传统方案中，两输入端中的一端输入激光相干态，而另一端不作输入。接下来给出3个达到SQL精度的量子态的例子。

1）入射态为相干态与真空态 $| α〉 | 0〉$ 时，| $α〉$ = $\hat{D} (α) | 0〉 = e x p (α {\hat{a}}^{†} - α * \hat{a}) | 0〉$ 。经过BS后，该量子态变为 $| α / \sqrt[]{2}, α / \sqrt[]{2}〉$ ，该量子态对算符 ${\hat{J}}_{z}$ 的方差 $Δ^{2} {\hat{J}}_{z} = | α |^{2} / 4 = N / 4$ 。因此，利用相干态测量相位可以达到SQL，这也是经典光学能达到的最优精度。

2）当入射态为Fock态与真空态 $| N〉 | 0〉$ 时，经过BS后该量子态变为

| N〉 | 0〉 \to \sum_{n = 0}^{N} \sqrt[]{\frac{C_{N}^{n}}{2^{N}}} | n〉 | N - n〉

。（18）

演化后的量子态对算符 ${\hat{J}}_{z}$ 的方差 $Δ^{2} {\hat{J}}_{z} = | α |^{2} / 4 = N / 4$ 。因此，该量子态测量相位的精度与相干态相同。

3）当入射态为单光子态与真空态 $| 1〉 | 0〉$ 时，经过BS后量子态变为 $(| 1〉 | 0〉 + | 0〉 | 1〉) / \sqrt[]{2}$ 。该量子态的量子Fisher信息为1。因此，若连续入射N个单光子，由Fisher信息的叠加性质可知其对相位的测量精度也达到SQL。

1981年，Caves^［54］指出，不作输入的端口由于真空涨落，使得相位的探测精度被限制在SQL。若真空态一端输入压缩态^［55-56］，可以提供超越SQL的相位测量精度，从而开启了对非经典光学态在相位测量上的量子精密测量优势的研究。当一端输入压缩态另一端输入相干态时，量子态为

| α〉 | r〉 = {\hat{D}}_{a} (α) {\hat{S}}_{b} (r) | 0〉 | 0〉

，（19）

式中： $| r〉 = 1 / \sqrt[]{c o s h | r |} \sum_{n = 0}^{\infty} t a n h^{n} | r | \sqrt[]{(2 n)!} / (2^{n} n!) | 2 n〉$ 。

该量子态经过BS后产生的量子态的量子Fisher信息为^{［1，57-58］}

Q_{f}^{s q} = | α |^{2} e^{2 r} + s i n h^{2} r

。（20）

如固定相干态与压缩态的总平均光子数为N，即 $| α |^{2} + s i n h^{2} r = N$ ，则针对二者平均光子数的比例进行优化，其量子Fisher信息式（20）可以达到 $N^{2}$ 量级，且该精度可以由光子数可分辨探测^［59］或平衡零差探测达到^［60］。而当输入两个端口的量子态为两个压缩态 $| r〉 | r〉$ 时（每一个压缩态的平均光子数 $s i n h^{2} r = N / 2$ ），该量子态可以达到的最终量子极限精度为

Δ ϕ \geq \frac{1}{\sqrt[]{N (N + 2)}} \approx \frac{1}{N}

，（21）

也可以达到HL^［61］。

基于上述原理，多个课题组利用压缩光，在实验上验证了超越SQL的相位测量精度^［62-67］。

上述讨论的方案之中，用到的光学干涉仪为SU（2）型干涉仪。如将SU（2）型干涉仪中两个BS替换为参量放大器，利用非线性过程产生非经典光学态，也可以提升相位测量精度，这种干涉仪称为SU（1，1）型干涉仪。该种干涉仪最早由Yurke等^［4］提出，然而该方案由于入射为真空态，因而平均光子数较低，仅在原理上可以达到HL。直到Plick等^［68］与Ou^［69］提出相干态入射的SU（1，1）型干涉仪才将该方案推向应用，并在原子与光学系统中实现^［70-77］。

除了压缩态外，还存在可以达到HL的最大纠缠态，称为NOON态。上述光学干涉仪的基本理论揭示了相位参数对应的产生算符（哈密顿量）为粒子数算符 $\hat{n}$ ，而由量子精密测量的基础理论可知，想要达到HL，最优的入射态为 $(| 0〉 + | N〉) / \sqrt[]{2}$ 。2022年，Wang等^［78］在超导系统中实现了不同Fock态的叠加。然而，光学系统中确定性地产生真空态与N光子Fock态的叠加非常困难，因此考虑一种相对容易产生的等效量子态，即NOON态^［79-80］：

\frac{| N 0〉 + | 0 N〉}{\sqrt[]{2}}

。（22）

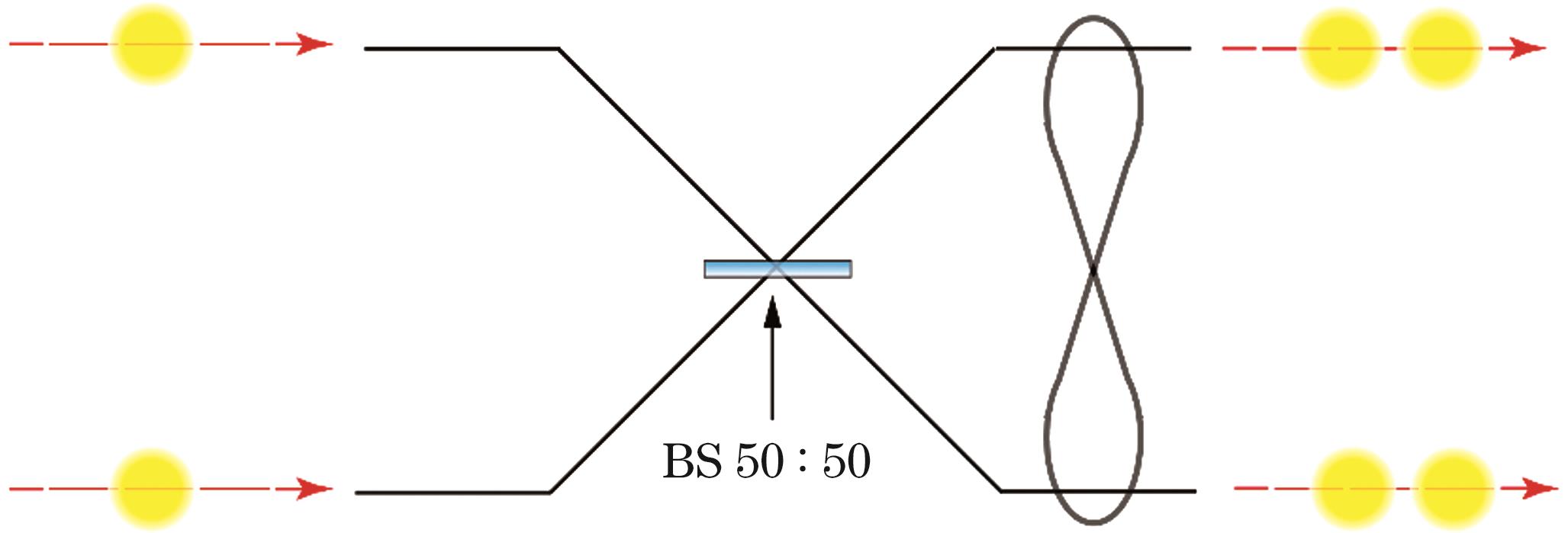
容易证明，该量子态可以达到HL。特别地，当N=2时，两光子NOON态可以确定性地由两光子干涉产生，即Hong-Ou-Mandel干涉（HOMI）^［81］。如图5所示，两个全同光子打入50∶50的BS两端，则出射的光子将同时存在于透射路或反射路。因此可以形成两光子在两个路径上的最大纠缠态

\frac{| 02〉 - | 20〉}{\sqrt[]{2}}

。（23）

图 5. Hong-Ou-Mandel干涉的基本原理

Fig. 5. Fundamental principle of Hong-Ou-Mandel interference

下载图片查看所有图片

利用HOMI产生路径^［82-83］和偏振^［84］最大纠缠态已经在实验上得到验证。然而，除了两光子NOON态外，更高光子的NOON态目前还无法确定性地产生。2004年，Mitchell等^［85］首次在实验上通过后选择实现了3光子NOON态。之后，Takeuchi课题组Nagata等^［86］与Zeilinger课题组Walther等^［87］分别产生了路径纠缠和偏振纠缠的4光子NOON态。更高光子的NOON态可以由相干态与压缩态干涉产生，Silberberg课题组Afek等^［88］利用该方法产生了5光子NOON态。

除了MZI外，光学干涉仪还有其他不同种类，如Michelson干涉仪、Sagnac干涉仪等，如图6所示。不同种类的干涉仪虽然原理都是利用光学干涉效应测量相位，但结构各有优势，因而可以用于不同的科学任务。

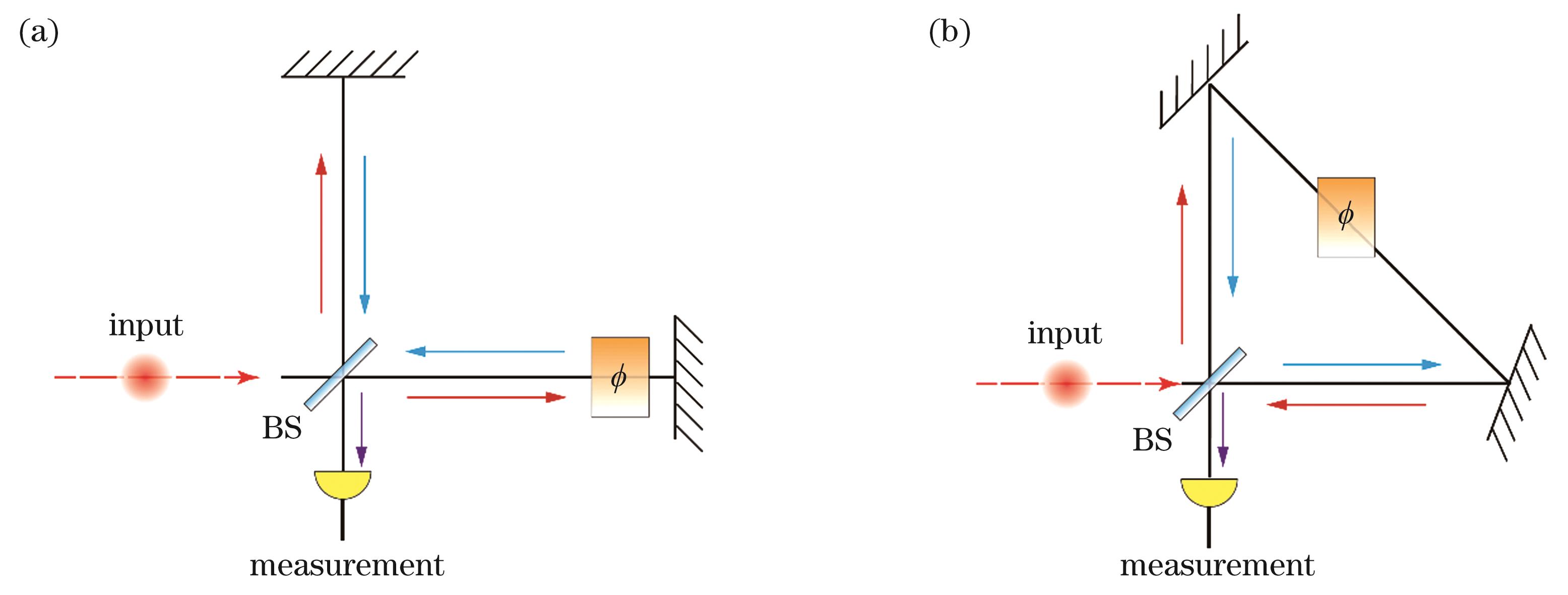
图 6. 不同类型的干涉仪结构。（a）Michelson干涉仪；（b）Sagnac干涉仪

Fig. 6. Structures of different types of interferometers. (a) Michelson interferometer; (b) Sagnac interferometer

下载图片查看所有图片

Michelson干涉仪的重要应用之一是引力波探测^{［67，89-92］}。宇宙中如黑洞合并等大事件的发生往往伴随时空畸变，从而辐射出引力波。当引力波来临时，会导致时空发生延展和收缩。利用类似于图6（a）中的Michelson干涉仪结构，干涉仪两臂上会产生相位差，干涉后的强度探测可以测量该相位差从而提取引力波的信息。引力波传播到地球后往往强度很弱（首次探测到的引力波强度用应变表示大约为3.4×10^-22［91］），甚至多数时候会低于探测器噪声。因此，用以探测引力波的Michelson干涉仪两臂长度要足够长，并且内部噪声要足够低。当干涉仪输入的光场为相干态时，对相位的探测精度为SQL，此时提升探测精度就需要增加激光强度以提升平均光子数。然而强激光同样会导致端镜受到的辐射压力变大，从而使干涉仪内部噪声增大。与MZI相似，当调整入射态为压缩态时，可以在不显著提升入射光强的情况下提升对引力波探测的灵敏度。2011年，激光干涉引力波天文台（LIGO）在600 m的干涉仪输入端注入压缩光的方式将干涉仪内部噪声减少了超过3.5 dB^［93］，然而该工作探测频率在700 Hz。2013年，LIGO进一步提升装置适用范围，将探测频率降低至150 Hz^［10］，并于2019年首次利用该方案探测到引力波^［94］。

还有一类特殊的干涉仪为Sagnac干涉仪，如图6（b）所示。Sagnac干涉仪的一个重要应用为量子陀螺^［95］。若干涉仪装置在整体旋转时，入射量子态在干涉仪内部按照不同方向传输的过程中会产生与装置的旋转速度线性相关的相位差，此时利用干涉效应可以对旋转速度参数进行精准测量^［96-97］。同样可以利用注入非经典光学态的方式实现对旋转速度参数的量子增强测量。如2010年Schnabel等^［98］利用在另一个端口注入压缩态的方式，将散粒噪声减少了4.5 dB。2022年Jiao等^［99］提出在有噪声环境下利用双模压缩态注入的方式，恢复旋转速度参数的超海森堡极限精度。2023年，Zhao等^［100］提出利用巢式SU（1，1）的结构将SU（1，1）干涉仪与Sagnac干涉仪相结合，增强对旋转速度的测量。

3.3　存在损耗的光学干涉仪中相位测量的量子极限

尽管NOON态对相位的测量具有经典光学态难以比拟的精度优势，然而若是外界存在噪声，如损耗或退相干等，则NOON态的精度会迅速降低。对于相干态来说，损耗的存在只会在SQL上附加一个系数而变为 $1 / \sqrt[]{η N}$ ，而NOON态则会直接影响比例，并且当光子数高时，NOON态对相位的测量精度甚至会差于SQL^［101］。损耗的一般模型如图7所示，此处的损耗存在于加载相位一端，并且损耗的模型可以由BS的模型来描述。

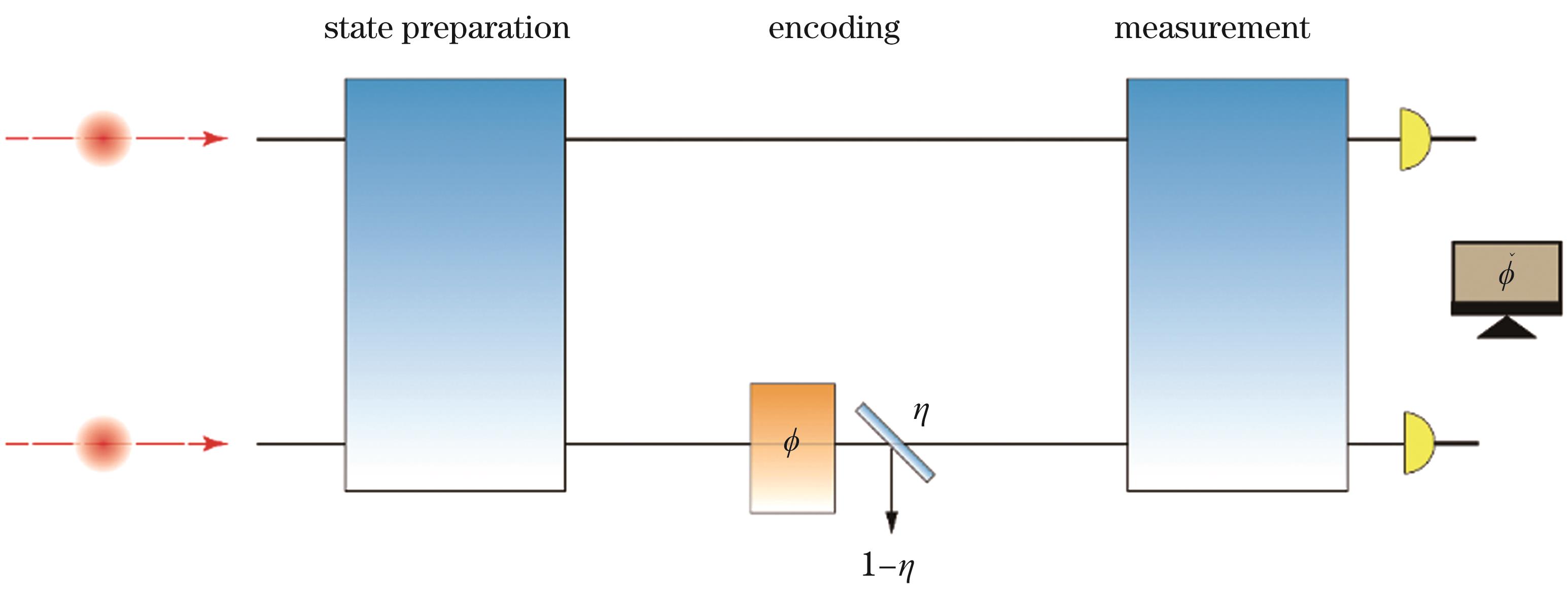
图 7. 存在损耗的光学干涉仪，加载相位的位置透过率为 $η$

Fig. 7. Lossy optical interferometer with transmissivity $η$ of encoding phase

下载图片查看所有图片

若考虑固定光子数为N的一般两模式量子态

| ψ_{N}〉 = \sum_{n = 0}^{N} c_{n} | n, N - n〉

。（24）

当 $c_{0} = c_{N} = 1 / \sqrt[]{2}$ ，其余系数为0时，该量子态即为NOON态。当无损耗时，该一般形式量子态对应的量子Fisher信息由式（9）计算得出为 $4 [\sum_{n = 0}^{N} n^{2} c_{n} - (\sum_{n = 0}^{N} n c_{n})^{2}]$ 。优化该形式得到的最优系数刚好为NOON态。当存在损耗时，量子态变为不同光子数态的直和^［102］，直和的各个量子态的光子数从0到N分别对应损耗到环境中不同数目的光子。当存在损耗时，NOON态的测量精度会有 $η^{N}$ 的降低，因此并不是式（23）中量子态的最优选择。Kacprowicz等^［103］在实验上验证了在有损耗情况下最优的两光子态对相位测量的最优精度。除了在干涉仪内部存在损耗外，态制备与探测端也都可能存在损耗，并且Datta等^［104］证明这两种损耗对于精度的影响是相同的。Spagnolo等^［105］在探测器存在损耗的条件下在实验上实现了对相位的精确测量。针对超越SQL实现相位测量的量子优越的问题，Resch等^［106］给出了系统损耗与光子的干涉对比度需要满足的关系：

η_{t o t a l} V^{2} N > 1

，（25）

式中： $η_{t o t a l}$ 代表整个系统的透过率，包括考虑了态制备与探测端的探测效率；V为光子的干涉对比度。

在上述条件下，真正意义上突破SQL的实验于2017年由Pryde课题组Slussarenko等^［107］完成。在他们的实验中，基于偏振的两光子NOON态，利用低损耗光学元件、高探测效率探测器、高对比度光源实现了对SQL的无条件突破，实验中 $η_{t o t a l} V^{2} N \approx$ 1.23。

NOON态不抗损耗、难以制备，因此研究者们除了致力于研究如何制备高光子数NOON态，也在研究替代NOON态的更抗损耗、易于制备的替代光学态。Holland与Burnett^［2］于1993年首次提出将两个相同光子数的Fock态 $| N / 2, N / 2〉$ 输入到BS的两端产生的量子态（称为HB态）可以达到HL，其形式为

| ψ_{H B}〉 = \sum_{n = 0}^{\frac{N}{2}} \frac{\sqrt[]{(2 n)! (N - 2 n)!}}{2^{N / 2} n! (N / 2 - n)!} | 2 n, N - 2 n〉

。（26）

2011年，Datta等^［104］证明了HB态在干涉仪存在损耗时，依旧能保持超越SQL的测量精度。多个课题组在实验上实现了多光子HB态并进行了相位测量实验^{［108-110］}。

上述方案都是在已知损耗的情况下，针对特定损耗提升相位测量精度的手段。若探测端与态制备阶段的损耗可以提前标定，已知损耗的情形是合理的，然而若加载相位的过程中存在无法提前标定的损耗，则损耗与相位均为系统中的未知参数。因此，在这种情况下问题变为针对损耗和相位的多参数估计问题，多参数量子精密测量将在下文详细介绍。针对损耗和相位联合测量的精度制约关系由Crowley等^［111］首次给出，他们同时给出了能够达到联合测量的最优精度的量子态。

3.4　多参数量子精密测量

上述量子精密测量的基础理论与应用都针对单一参数的幺正编码。然而，一般的物理过程往往包含不止一个参数。类似于单参数量子精密测量，利用量子资源对多个参数的精密测量同样具有量子优势^{［112-113］}。

考虑到待估计的d个未知参数 $x = (x_{1}, x_{2}, \dots, x_{d})^{T}$ ，类似于单参数量子精密测量的一般过程，首先准备一个初始态 $ρ_{0}$ 用于感知参数得到末态 $ρ_{x}$ ，针对末态进行测量 ${{\hat{E}}_{i}}$ 得到测量结果，得到测量结果i的概率为 $p (i | x) = T r [ρ_{x} {\hat{E}}_{i}]$ 。根据每一次的测量结果我们可以实现对这d个未知参数的估计，并利用协方差矩阵衡量多个参数估计精度：

σ = {\sum_{i} (x_{e s t} - x) (x_{e s t} - x)}^{T} p (i | x)

，（27）

其中协方差矩阵的对角项代表相应参数的估计方差，而非对角项则代表不同参数之间的关联。

根据概率分布可以计算得到Fisher信息矩阵 $F$ ，对应的矩阵元素为

F_{p q} = \sum_{i} \frac{1}{p (i | x)} \frac{\partial p (i | x)}{\partial x_{p}} \frac{\partial p (i | x)}{\partial x_{q}}

。（28）

$F$ 是d×d的半正定对称矩阵。同样的，根据量子态 $ρ_{x}$ 也可以计算其量子Fisher信息矩阵，其元素为

Q_{p q} = \sum_{m, n = 0} \frac{2 R e (〈ψ_{n} | \partial_{x_{p}} ρ_{x} | ψ_{m}〉 〈ψ_{m} | \partial_{x_{q}} ρ_{x} | ψ_{n}〉)}{λ_{m} + λ_{n}}

。（29）

若末态为纯态 $| ψ_{x}〉$ ，则量子Fisher信息可以简化为

Q_{p q} = 4 R e (〈\partial_{x_{p}} ψ_{x} | \partial_{x_{q}} ψ_{x}〉 - 〈\partial_{x_{p}} ψ_{x} | ψ〉 〈ψ | \partial_{x_{q}} ψ_{x}〉)

。（30）

协方差矩阵、Fisher信息矩阵与量子Fisher信息矩阵之间的相互关系可以由不等式给出：

σ \geq \frac{F^{- 1}}{ν} \geq \frac{Q^{- 1}}{ν}

。（31）

式（31）中第一个不等式与单参数情形相同，合适的估计方式总可以饱和该不等式。然而第二个不等式，即Fisher信息与量子Fisher信息的相等关系需要满足弱对易条件^［26］：

T r [ρ_{x} [{\hat{L}}_{x_{p}}, {\hat{L}}_{x_{q}}]] = 0, \forall p, q

。（32）

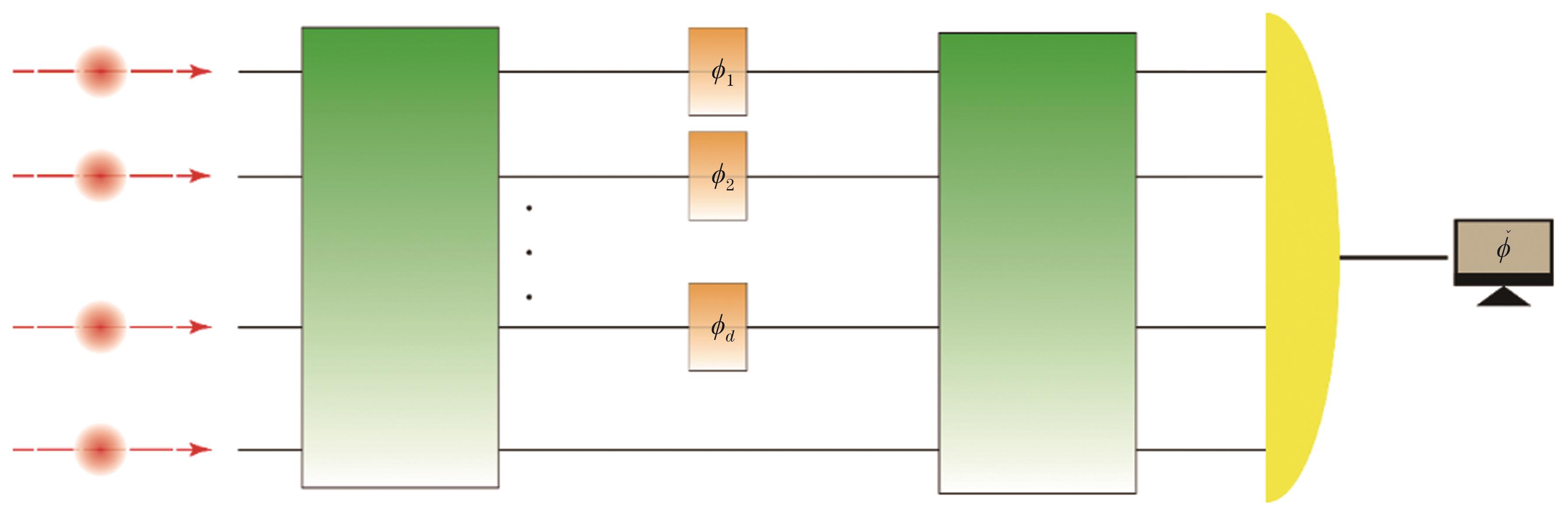
多参数量子精密测量目前也有众多应用，其中最为广泛的应用是针对多个相位进行联合测量。多相位的耦合过程（如图8所示）可以由幺正演化来描述： $U (ϕ) = e x p (- i \sum_{k = 1}^{d} {\hat{n}}_{k} ϕ_{k})$ ，其中 ${\hat{n}}_{k}$ 代表不同模式上的粒子数算符。

图 8. 多相位估计示意图

Fig. 8. Schematic of multiple phases estimation

下载图片查看所有图片

由于不同模式之间的粒子数算符相互对易，因此多相位量子精密测量问题中的量子Fisher信息往往都可以达到。多相位量子精密测量的优越性在于利用量子资源对多个相位的联合估计会超越将资源平分到每一个相位最终得到的各个相位的精度之和。Humphreys等^［113］首先讨论了多相位联合估计的精度问题。他们考虑当利用N个光子估计d个相位时，若每个相位都采用N/d光子NOON态时，能够达到的各个相位方差之和为 $d^{3} / N^{2}$ 。然而，利用多光子多模式纠缠态能够对各个相位测量达到的最小方差为 ${(1 + \sqrt[]{d})}^{2} d / (4 N^{2})$ ，相比于各个相位的同时测量，该精度有显著提升。达到最小方差的量子态为多模式NOON态：

| ψ_{o p t i m a l}〉 = β_{1} (| N, 0, \dots, 0〉 + | 0, N, \dots, 0〉 + \dots + | 0, \dots, N, 0〉) + β_{2} | 0, \dots, 0, N〉

，（33）

式中： $β_{1} = 1 / \sqrt[]{d + \sqrt[]{d}}$ ； $β_{2} = \sqrt[]{d / (d + \sqrt[]{d})}$ 。

2021年，Hong等^［114］在实验上利用基于SPDC产生的光子偏振纠缠态在BS上的干涉产生了均匀权重（ $β_{1} = 1 / 2$ ）的四模式两光子NOON态用于估计三个相位，该量子态同样具有超越单独估计各个相位精度之和的测量精度。2022年，Hong等^［115］又基于后选择的方式，从上述四模式两光子NOON态中挑选三个模式并对相对权重进行了调整，从而实现了与式（33）相同的对两个相位最优的量子态制备。Polino等^［116］在光芯片上首次实现了利用双光子对两个相位的联合测量。而后该课题组又利用单光子输入与贝叶斯自适应反馈算法实现了多个相位的联合测量^［117］。

除了针对多个相位的同时估计外，实际应用中往往还关注多个相位的整体组合，如平均值等的测量。因此，这种分布式传感也是近些年来研究的重点^［118］。对于需要感知的d个不同的相位，考虑其任意叠加

\bar{ϕ} = \sum_{j} w_{j} ϕ_{j}

。（34）

分布式传感的任务就是利用量子资源针对该任意叠加的相位进行量子增强测量。Ge等^［119］证明利用非纠缠态输入线性光网络可以达到 $2 / [N (N + 2)]$ 的方差下限。Gross等^［120］从信息几何的角度出发，通过分析叠加后相位的产生算符给出了最优入射态为多模式纠缠态。2021年，Pan课题组Liu等^［121］在实验上利用六光子偏振纠缠态实现分布式传感，误差相较于SQL降低了2.7 dB。除了利用光子数纠缠态提升分布式传感的精度外，利用压缩态提升传感精度也有相对应的研究^{［122-123］}。对分布式传感的研究也被拓展到对多个线性方程的同时估计^［124］。

针对相位的多参数量子精密测量除了多相位外，还有针对相位和损耗的联合估计。上文提到的针对相位和损耗的弱对易条件并不满足，因此损耗和相位的量子Fisher信息矩阵给出的精度无法达到。2019年Albarelli等^［125］利用凸优化算法给出了当弱对易条件不满足时多个参数能够达到的最终测量极限精度，即Holevo Cramér-Rao下界（HCRB）^{［18，126-129］}。该工作同时以损耗与相位为例，给出了单光子同时测量损耗与相位的联合方差下界。然而HCRB是针对多个拷贝的联合测量，原则上混合态需要达到HCRB的测量是作用在无穷多拷贝量子态上的联合测量或称为纠缠测量^{［21，130-134］}。因此，寻找单一拷贝下对多个参数测量的最优测量是重要的研究方向。2021年，Conlon等^［135］提出用算法求解单一拷贝下多参数测量最优精度Nagaoka-Hayashi下界，并给出了达到损耗与相位联合估计精度最优的测量方案。

除了损耗与相位外，另一个影响相位估计精度的是相位本身的涨落，相位涨落本身会导致退相干^{［136-139］}。若在量子比特［ $c o s (θ / 2) | 0〉 + s i n (θ / 2) | 1〉$ ］中，相位本身加载的过程中服从中心相位为 $ϕ_{0}$ ，标准差为 $Δ$ 的高斯分布，则该量子态会发生退相干，退相干系数与 $Δ$ 相关，则末态为

ρ_{f} = (\begin{matrix} c o s^{2} (\frac{θ}{2}) & s i n \frac{θ}{2} c o s \frac{θ}{2} e x p (- i ϕ_{0} - Δ^{2}) \\ c o s \frac{θ}{2} s i n \frac{θ}{2} e x p (i ϕ_{0} - Δ^{2}) & s i n^{2} (\frac{θ}{2}) \end{matrix})

。（35）

针对参数 $ϕ_{0}$ 与 $Δ$ ，只有当 $θ = π / 2$ 时弱对易条件才能满足。2014年，Vidrighin等^［140］在单一拷贝的情况下实现了对这二者的联合估计。由HCRB可知，该量子态在多拷贝的联合测量下可以提升对这两个参数的测量精度，Barbier课题组Roccia等^［141］针对两个量子比特非确定的纠缠测量给出了验证，并证明在他们的测量装置中，对相位和涨落参数具有超越单一拷贝的测量精度。

3.5　光量子精密测量的其他应用

除了光子的偏振自由度和光子数自由度外，光子还有轨道角动量^{［142-144］}、空间模式、时间频率^{［145-151］}自由度等。利用光子的其余自由度也可以实现精密测量，例如利用光子的轨道角动量提升对旋转参数的测量^［152］，利用厄米-高斯模式测量光束位移与旋转等^［153］。

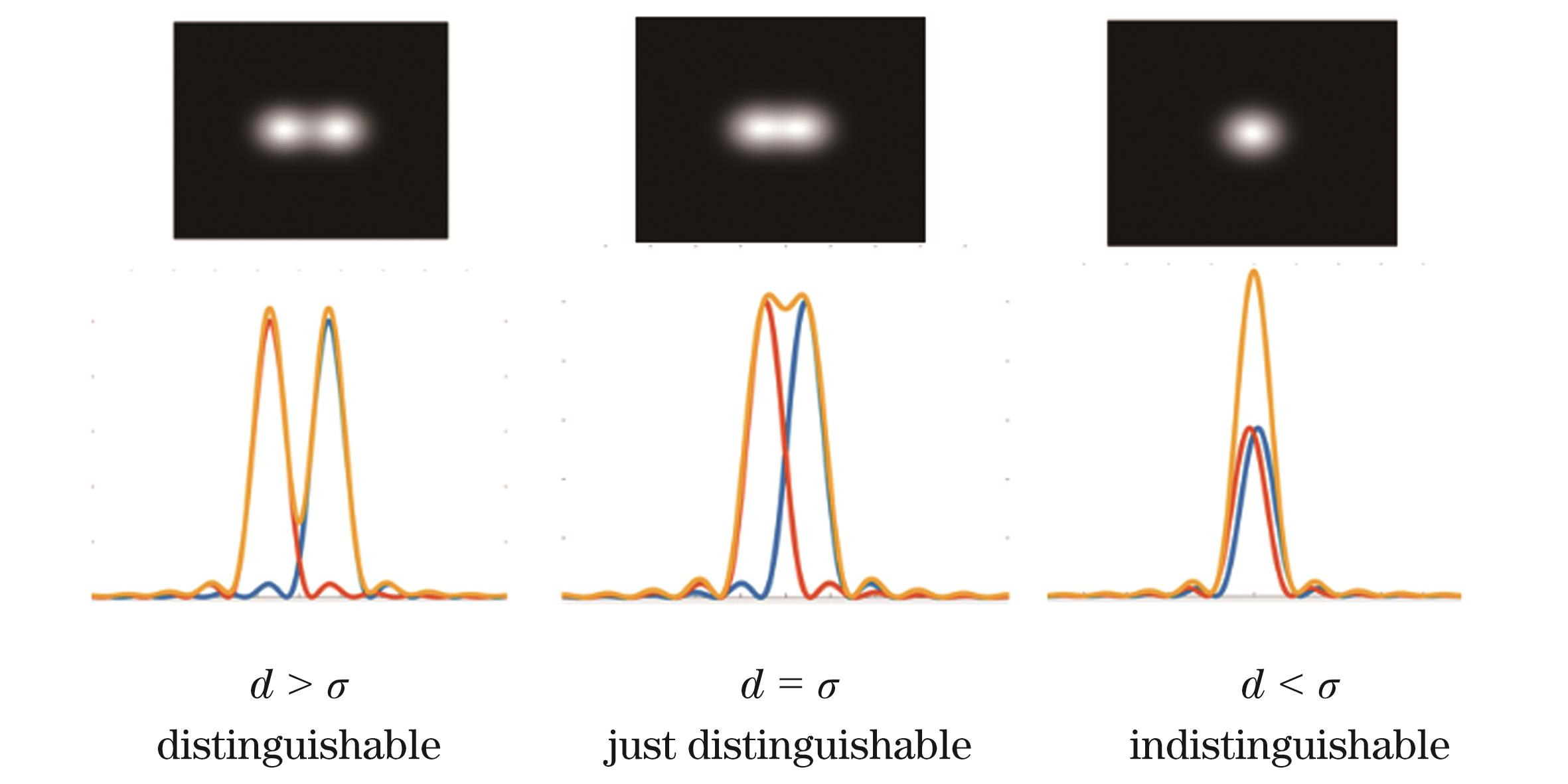
光子作为人类感知外界信息的载体，用于成像是其重要作用之一。在经典成像问题中，瑞利判据给出了系统的最终分辨率极限，即两非相干点光源的分离距离相比于该系统的点扩散函数的大小关系发生改变时，分别对应着可分辨、恰好可分辨以及不可分辨，如图9所示。2016年，Tsang等^［154］针对该问题进行了量子建模，得到两个非相干点光源的量子态为

ρ_{s} = \frac{1}{2} (| ψ_{-}〉 〈ψ_{-} | + | ψ_{+}〉 〈ψ_{+} |)

，（36）

式中： $| ψ_{\pm}〉 = \int d x ψ (x \pm s / 2) {\hat{a}}^{†} (x) | 0〉$ 。

图 9. 经典成像系统中的Rayleigh判据

Fig. 9. Rayleigh criterion in classical imaging systems

下载图片查看所有图片

传统的测量方案是直接将该量子态投影到位置 $| x〉$ 上，可以得到其经典强度探测的Fisher信息。Tsang等^［154］指出，当分离距离参数s减小时，经典测量的Fisher信息会趋近于0，这个结论与瑞利判据相符。然而，通过计算该量子态的量子Fisher信息，发现其针对分离参数的量子极限精度不受分离距离的影响，始终保持定值，并且通过空间模式解复用的测量方案可以达到该量子极限。随后相关研究人员将该问题拓展到三维分辨^{［155-158］}、非等光强点光源分辨^{［159-161］}、多点光源^［162］以及具有部分相干性点光源分辨^{［163-167］}的问题中去。对于非相干点光源分辨问题的量子建模启发了一系列针对非相干成像问题的新型量子测量方案。

2016年，Paúr等^［168］利用干涉全息图实现了对两个非相干点光源距离的估计突破经典极限，并达到了量子极限。Tham等^［169］则通过附加相位的方法提升针对分离参数的测量精度。此外还有双光子干涉^［170］、外差探测^［171］、翻折干涉^［172］等新型探测手段提升分离参数的估计精度。上述实验方案往往只能将量子态投影到少数几个模式中，因而无法进行真正的成像。Treps课题组Rouvière等^{［173-174］}利用多平面转换技术，将光场投影到多个厄米-高斯模式上，并用于非相干点光源分辨中。

除成像外，利用光子的多自由度对其他物理系统进行量子模拟，从而模拟系统在量子精密测量领域的应用也是一个重要的研究方向。2019年，Hou等^［175］利用光子的偏振和路径自由度制备模式之间的最大纠缠态，利用最优控制的方式实现了对磁场系统参数的模拟测量，并使其测量精度接近HL。2021年，他们又将该问题拓展到多个参数，并实现了没有精度制约关系的多参数测量精度极限，方差有13.27 dB的提升^［176］。

4　结语

量子精密测量是量子力学在信息技术领域的重要应用，与量子计算、量子保密通信并称三大量子科技，是未来量子技术发展的重要研究方向。

本文重点回顾了光量子精密测量的基本原理与相关应用，重点针对光学相位参数的量子增强测量方案进行了总结和分析。量子精密测量的一般步骤是：态制备、参数耦合、测量。提升参数估计精度可以针对上述步骤的每个方面进行优化，这也是量子精密测量研究的重要逻辑。

作为测量光学相位的重要科学装置，光学干涉仪是光量子精密测量中的常见装置。针对光学干涉仪中的相位测量问题，在态制备过程中利用纠缠、压缩等量子资源可以使相位测量方差随粒子数以 $N^{2}$ 的比例减少，实现超越标准量子极限达到海森堡极限的目标。本文还回顾了当干涉仪存在损耗时，相关研究工作如何提升相位测量精度的努力，其中包括利用具有噪声鲁棒性的量子态测量相位以及将损耗一并考虑看作多参数估计问题。除单一相位参数外，多相位、多相位线性组合、相位与损耗、相位与相位涨落的估计等问题近些年来也受到广泛关注。相关工作为相位精密测量的实际应用提供了巨大推力。除了相位测量外，光量子精密测量还在成像、模拟等领域发挥重要作用，并有望在未来真正推广到工程应用中去。

参考文献

[1] Pezzé L, Smerzi A. Mach-Zehnder interferometry at the Heisenberg limit with coherent and squeezed-vacuum light[J]. Physical Review Letters, 2008, 100(7): 073601.

[2] Holland M J, Burnett K. Interferometric detection of optical phase shifts at the Heisenberg limit[J]. Physical Review Letters, 1993, 71(9): 1355-1358.

[3] Ou Z Y. Fundamental quantum limit in precision phase measurement[J]. Physical Review A, 1997, 55(4): 2598-2609.

[4] Yurke B, McCall S L, Klauder J R. SU(2) and SU(1,1) interferometers[J]. Physical Review A, 1986, 33(6): 4033-4054.

[5] Chen G, Aharon N, Sun Y N, et al. Heisenberg-scaling measurement of the single-photon Kerr non-linearity using mixed states[J]. Nature Communications, 2018, 9: 93.

[6] Chen G, Zhang L J, Zhang W H, et al. Achieving Heisenberg-scaling precision with projective measurement on single photons[J]. Physical Review Letters, 2018, 121(6): 060506.

[7] Zhang L J, Datta A, Walmsley I A. Precision metrology using weak measurements[J]. Physical Review Letters, 2015, 114(21): 210801.

[8] Xu L, Liu Z X, Datta A, et al. Approaching quantum-limited metrology with imperfect detectors by using weak-value amplification[J]. Physical Review Letters, 2020, 125(8): 080501.

[9] Abadie J, Abbott B P, Abbott R, et al. A gravitational wave observatory operating beyond the quantum shot-noise limit[J]. Nature Physics, 2011, 7: 962-965.

[10] Aasi J, Abadie J, Abbott B P, et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light[J]. Nature Photonics, 2013, 7: 613-619.

[11] Degen C L, Reinhard F, Cappellaro P. Quantum sensing[J]. Reviews of Modern Physics, 2017, 89(3): 035002.

[12] Pezzè L, Smerzi A, Oberthaler M K, et al. Quantum metrology with nonclassical states of atomic ensembles[J]. Reviews of Modern Physics, 2018, 90(3): 035005.

[13] Polino E, Valeri M, Spagnolo N, et al. Photonic quantum metrology[J]. AVS Quantum Science, 2020, 2(2): 024703.

[14] Liu J, Yuan H D, Lu X M, et al. Quantum Fisher information matrix and multiparameter estimation[J]. Journal of Physics A: Mathematical and Theoretical, 2020, 53(2): 023001.

[15] Braunstein S L, Caves C M. Statistical distance and the geometry of quantum states[J]. Physical Review Letters, 1994, 72(22): 3439-3443.

[16] Fujiwara A. Strong consistency and asymptotic efficiency for adaptive quantum estimation problems[J]. Journal of Physics A: Mathematical and Theoretical, 2011, 44(7): 079501.

[17] Gill R D, Massar S. State estimation for large ensembles[J]. Physical Review A, 2000, 61(4): 042312.

[18] Hayashi M, Matsumoto K. Asymptotic performance of optimal state estimation in qubit system[J]. Journal of Mathematical Physics, 2008, 49(10): 102101.

[19] Giovannetti V, Lloyd S, Maccone L. Quantum metrology[J]. Physical Review Letters, 2006, 96(1): 010401.

[20] Giovannetti V, Lloyd S, Maccone L. Advances in quantum metrology[J]. Nature Photonics, 2011, 5: 222-229.

[21] Hou Z B, Tang J F, Shang J W, et al. Deterministic realization of collective measurements via photonic quantum walks[J]. Nature Communications, 2018, 9: 1414.

[22] Perarnau-Llobet M, Bäumer E, Hovhannisyan K V, et al. No-go theorem for the characterization of work fluctuations in coherent quantum systems[J]. Physical Review Letters, 2017, 118(7): 070601.

[23] Wu K D, Bäumer E, Tang J F, et al. Minimizing backaction through entangled measurements[J]. Physical Review Letters, 2020, 125(21): 210401.

[24] Gisin N, Popescu S. Spin flips and quantum information for antiparallel spins[J]. Physical Review Letters, 1999, 83(2): 432-435.

[25] Tang J F, Hou Z B, Shang J W, et al. Experimental optimal orienteering via parallel and antiparallel spins[J]. Physical Review Letters, 2020, 124(6): 060502.

[26] Demkowicz-Dobrzański R, Górecki W, Guţă M. Multi-parameter estimation beyond quantum Fisher information[J]. Journal of Physics A: Mathematical and Theoretical, 2020, 53(36): 363001.

[27] Ji Z F, Wang G M, Duan R Y, et al. Parameter estimation of quantum channels[J]. IEEE Transactions on Information Theory, 2008, 54(11): 5172-5185.

[28] de Burgh M, Bartlett S D. Quantum methods for clock synchronization: beating the standard quantum limit without entanglement[J]. Physical Review A, 2005, 72(4): 042301.

[29] Higgins B L, Berry D W, Bartlett S D, et al. Entanglement-free Heisenberg-limited phase estimation[J]. Nature, 2007, 450(7168): 393-396.

[30] Braun D, Adesso G, Benatti F, et al. Quantum-enhanced measurements without entanglement[J]. Reviews of Modern Physics, 2018, 90(3): 035006.

[31] Escher B M, de Matos Filho R L, Davidovich L. General framework for estimating the ultimate precision limit in noisy quantum-enhanced metrology[J]. Nature Physics, 2011, 7: 406-411.

[32] Escher B M, de Matos Filho R L, Davidovich L. Quantum metrology for noisy systems[J]. Brazilian Journal of Physics, 2011, 41(4): 229-247.

[33] Demkowicz-Dobrzański R, Kołodyński J, Guţă M. The elusive Heisenberg limit in quantum-enhanced metrology[J]. Nature Communications, 2012, 3: 1063.

[34] Walmsley I A. Quantum optics: science and technology in a new light[J]. Science, 2015, 348(6234): 525-530.

[35] Pan J W, Chen Z B, Lu C Y, et al. Multiphoton entanglement and interferometry[J]. Reviews of Modern Physics, 2012, 84(2): 777-838.

[36] O’Brien J L, Furusawa A, Vučković J. Photonic quantum technologies[J]. Nature Photonics, 2009, 3: 687-695.

[37] Kwiat P G, Mattle K, Weinfurter H, et al. New high-intensity source of polarization-entangled photon pairs[J]. Physical Review Letters, 1995, 75(24): 4337-4341.

[38] Ou Z Y, Pereira S F, Kimble H J, et al. Realization of the Einstein-Podolsky-Rosen paradox for continuous variables[J]. Physical Review Letters, 1992, 68(25): 3663-3666.

[39] Bouwmeester D, Pan J W, Mattle K, et al. Experimental quantum teleportation[J]. Nature, 1997, 390(6660): 575-579.

[40] Furusawa A, Sorensen J L, Braunstein S L, et al. Unconditional quantum teleportation[J]. Science, 1998, 282(5389): 706-709.

[41] Flamini F, Spagnolo N, Sciarrino F. Photonic quantum information processing: a review[J]. Reports on Progress in Physics, 2019, 82(1): 016001.

[42] Slussarenko S, Pryde G J. Photonic quantum information processing: a concise review[J]. Applied Physics Reviews, 2019, 6(4): 041303.

[43] Ono T, Okamoto R, Takeuchi S. An entanglement-enhanced microscope[J]. Nature Communications, 2013, 4: 2426.

[44] Brambilla E, Caspani L, Jedrkiewicz O, et al. High-sensitivity imaging with multi-mode twin beams[J]. Physical Review A, 2008, 77(5): 053807.

[45] Gregory T, Moreau P A, Toninelli E, et al. Imaging through noise with quantum illumination[J]. Science Advances, 2020, 6(6): eaay2652.

[46] Moreau P A, Toninelli E, Gregory T, et al. Imaging with quantum states of light[J]. Nature Reviews Physics, 2019, 1: 367-380.

[47] Berchera I R, Degiovanni I P. Quantum imaging with sub-Poissonian light: challenges and perspectives in optical metrology[J]. Metrologia, 2019, 56(2): 024001.

[48] Genovese M. Real applications of quantum imaging[J]. Journal of Optics, 2016, 18(7): 073002.

[49] Samantaray N, Ruo-Berchera I, Meda A, et al. Realization of the first sub-shot-noise wide field microscope[J]. Light, Science & Applications, 2017, 6(7): e17005.

[50] Giovannetti V, Lloyd S, Maccone L, et al. Sub-Rayleigh-diffraction-bound quantum imaging[J]. Physical Review A, 2009, 79(1): 013827.

[51] Tenne R, Rossman U, Rephael B, et al. Super-resolution enhancement by quantum image scanning microscopy[J]. Nature Photonics, 2019, 13: 116-122.

[52] Treps N, Andersen U, Buchler B, et al. Surpassing the standard quantum limit for optical imaging using nonclassical multimode light[J]. Physical Review Letters, 2002, 88(20): 203601.

[53] Kolobov M I. The spatial behavior of nonclassical light[J]. Reviews of Modern Physics, 1999, 71(5): 1539-1589.

[54] Caves C M. Quantum-mechanical noise in an interferometer[J]. Physical Review D, 1981, 23(8): 1693-1708.

[55] Braunstein S L, van Loock P. Quantum information with continuous variables[J]. Reviews of Modern Physics, 2005, 77(2): 513-577.

[56] Pirandola S, Bardhan B R, Gehring T, et al. Advances in photonic quantum sensing[J]. Nature Photonics, 2018, 12: 724-733.

[57] Ono T, Hofmann H F. Effects of photon losses on phase estimation near the Heisenberg limit using coherent light and squeezed vacuum[J]. Physical Review A, 2010, 81(3): 033819.

[58] Jarzyna M, Demkowicz-Dobrzański R. Quantum interferometry with and without an external phase reference[J]. Physical Review A, 2012, 85(1): 011801.

[59] Seshadreesan K P, Anisimov P M, Lee H, et al. Parity detection achieves the Heisenberg limit in interferometry with coherent mixed with squeezed vacuum light[J]. New Journal of Physics, 2011, 13(8): 083026.

[60] D’Ariano G M, Leonhardt U, Paul H. Homodyne detection of the density matrix of the radiation field[J]. Physical Review A, 1995, 52(3): R1801-R1804.

[61] Demkowicz-DobrzańskiR, JarzynaM, KołodyńskiJ. Quantum limits in optical interferometry[M]∥Progress in optics. Amsterdam: Elsevier, 2015: 345-435.

[62] Treps N, Grosse N, Bowen W, et al. A quantum laser pointer[J]. Science, 2003, 301(5635): 940-943.

[63] Grangier P, Slusher R E, Yurke B, et al. Squeezed-light-enhanced polarization interferometer[J]. Physical Review Letters, 1987, 59(19): 2153-2156.

[64] Xiao M, Wu L A, Kimble H J. Precision measurement beyond the shot-noise limit[J]. Physical Review Letters, 1987, 59(3): 278-281.

[65] McKenzie K, Shaddock D A, McClelland D E, et al. Experimental demonstration of a squeezing-enhanced power-recycled Michelson interferometer for gravitational wave detection[J]. Physical Review Letters, 2002, 88(23): 231102.

[66] Vahlbruch H, Chelkowski S, Hage B, et al. Demonstration of a squeezed-light-enhanced power- and signal-recycled Michelson interferometer[J]. Physical Review Letters, 2005, 95(21): 211102.

[67] Goda K, Miyakawa O, Mikhailov E E, et al. A quantum-enhanced prototype gravitational-wave detector[J]. Nature Physics, 2008, 4: 472-476.

[68] Plick W N, Dowling J P, Agarwal G S. Coherent-light-boosted, sub-shot noise, quantum interferometry[J]. New Journal of Physics, 2010, 12(8): 083014.

[69] Ou Z Y. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer[J]. Physical Review A, 2012, 85(2): 023815.

[70] Jing J T, Liu C J, Zhou Z F, et al. Realization of a nonlinear interferometer with parametric amplifiers[J]. Applied Physics Letters, 2011, 99(1): 011110.

[71] Hudelist F, Kong J, Liu C J, et al. Quantum metrology with parametric amplifier-based photon correlation interferometers[J]. Nature Communications, 2014, 5: 3049.

[72] Anderson B E, Gupta P, Schmittberger B L, et al. Phase sensing beyond the standard quantum limit with a variation on the SU(1,1) interferometer[J]. Optica, 2017, 4(7): 752-756.

[73] Manceau M, Leuchs G, Khalili F, et al. Detection loss tolerant supersensitive phase measurement with an SU(1,1) interferometer[J]. Physical Review Letters, 2017, 119(22): 223604.

[74] Guo X S, Li X Y, Liu N N, et al. Quantum information tapping using a fiber optical parametric amplifier with noise figure improved by correlated inputs[J]. Scientific Reports, 2016, 6: 30214.

[75] Lukens J M, Pooser R C, Peters N A. A broadband fiber-optic nonlinear interferometer[J]. Applied Physics Letters, 2018, 113(9): 091103.

[76] Liu Y H, Li J M, Cui L, et al. Loss-tolerant quantum dense metrology with SU(1,1) interferometer[J]. Optics Express, 2018, 26(21): 27705-27715.

[77] Lukens J M, Peters N A, Pooser R C. Naturally stable Sagnac-Michelson nonlinear interferometer[J]. Optics Letters, 2016, 41(23): 5438-5441.

[78] Wang W, Chen Z J, Liu X, et al. Quantum-enhanced radiometry via approximate quantum error correction[J]. Nature Communications, 2022, 13: 3214.

[79] Lee H, Kok P, Dowling J P. A quantum Rosetta Stone for interferometry[J]. Journal of Modern Optics, 2002, 49(14/15): 2325-2338.

[80] Bollinger J J, Itano W M, Wineland D J, et al. Optimal frequency measurements with maximally correlated states[J]. Physical Review A, 1996, 54(6): R4649-R4652.

[81] Hong C K, Ou Z Y, Mandel L. Measurement of subpicosecond time intervals between two photons by interference[J]. Physical Review Letters, 1987, 59(18): 2044-2046.

[82] Ou Z Y, Zou X Y, Wang L J, et al. Experiment on nonclassical fourth-order interference[J]. Physical Review A, 1990, 42(5): 2957-2965.

[83] Rarity J G, Tapster P R, Jakeman E, et al. Two-photon interference in a Mach-Zehnder interferometer[J]. Physical Review Letters, 1990, 65(11): 1348-1351.

[84] Kuzmich A, Mandel L. Sub-shot-noise interferometric measurements with two-photon states[J]. Quantum and Semiclassical Optics: Journal of the European Optical Society Part B, 1998, 10(3): 493-500.

[85] Mitchell M W, Lundeen J S, Steinberg A M. Super-resolving phase measurements with a multiphoton entangled state[J]. Nature, 2004, 429(6988): 161-164.

[86] Nagata T, Okamoto R, O’Brien J L, et al. Beating the standard quantum limit with four-entangled photons[J]. Science, 2007, 316(5825): 726-729.

[87] Walther P, Pan J W, Aspelmeyer M, et al. De Broglie wavelength of a non-local four-photon state[J]. Nature, 2004, 429(6988): 158-161.

[88] Afek I, Ambar O, Silberberg Y. High-NOON states by mixing quantum and classical light[J]. Science, 2010, 328(5980): 879-881.

[89] Schnabel R, Mavalvala N, McClelland D E, et al. Quantum metrology for gravitational wave astronomy[J]. Nature Communications, 2010, 1: 121.

[90] Abbott B P, Abbott R, Abbott T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 061102.

[91] Abbott B P, Abbott R, Abbott T D, et al. GW151226: observation of gravitational waves from a 22-solar-mass binary black hole coalescence[J]. Physical Review Letters, 2016, 116(24): 241103.

[92] Vahlbruch H, Wilken D, Mehmet M, et al. Laser power stabilization beyond the shot noise limit using squeezed light[J]. Physical Review Letters, 2018, 121(17): 173601.

[93] Abadie J, Abbott B P, Abbott R, et al. A gravitational wave observatory operating beyond the quantum shot-noise limit[J]. Nature Physics, 2011, 7: 962-965.

[94] Tse M, Yu H C, Kijbunchoo N, et al. Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy[J]. Physical Review Letters, 2019, 123(23): 231107.

[95] WangW, XiaJ L, XuY X. Research on integrated optical gyroscope[C]∥2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, December 10-12, 2008, Shenzhen, China. New York: IEEE Press, 2008.

[96] Khial P P, White A D, Hajimiri A. Nanophotonic optical gyroscope with reciprocal sensitivity enhancement[J]. Nature Photonics, 2018, 12: 671-675.

[97] Post E J. Sagnac effect[J]. Reviews of Modern Physics, 1967, 39(2): 475-493.

[98] Mehmet M, Eberle T, Steinlechner S, et al. Demonstration of a quantum-enhanced fiber Sagnac interferometer[J]. Optics Letters, 2010, 35(10): 1665-1667.

[99] Jiao L, An J-H. Noisy quantum gyroscope[J]. Photonics Research, 2023, 11(2): 150.

[100] Zhao W, Tang X, Guo X S, et al. Quantum entangled Sagnac interferometer[J]. Applied Physics Letters, 2023, 122(6): 064003.

[101] Dorner U, Demkowicz-Dobrzanski R, Smith B J, et al. Optimal quantum phase estimation[J]. Physical Review Letters, 2009, 102(4): 040403.

[102] Demkowicz-Dobrzanski R, Dorner U, Smith B J, et al. Quantum phase estimation with lossy interferometers[J]. Physical Review A, 2009, 80(1): 013825.

[103] Kacprowicz M, Demkowicz-Dobrzański R, Wasilewski W, et al. Experimental quantum-enhanced estimation of a lossy phase shift[J]. Nature Photonics, 2010, 4: 357-360.

[104] Datta A, Zhang L J, Thomas-Peter N, et al. Quantum metrology with imperfect states and detectors[J]. Physical Review A, 2011, 83(6): 063836.

[105] Spagnolo N, Vitelli C, Lucivero V G, et al. Phase estimation via quantum interferometry for noisy detectors[J]. Physical Review Letters, 2012, 108(23): 233602.

[106] Resch K J, Pregnell K L, Prevedel R, et al. Time-reversal and super-resolving phase measurements[J]. Physical Review Letters, 2007, 98(22): 223601.

[107] Slussarenko S, Weston M M, Chrzanowski H M, et al. Unconditional violation of the shot-noise limit in photonic quantum metrology[J]. Nature Photonics, 2017, 11: 700-703.

[108] Xiang G Y, Hofmann H F, Pryde G J. Optimal multi-photon phase sensing with a single interference fringe[J]. Scientific Reports, 2013, 3: 2684.

[109] Xiang G Y, Higgins B L, Berry D W, et al. Entanglement-enhanced measurement of a completely unknown optical phase[J]. Nature Photonics, 2011, 5: 43-47.

[110] Jin R B, Fujiwara M, Shimizu R, et al. Detection-dependent six-photon Holland-Burnett state interference[J]. Scientific Reports, 2016, 6: 36914.

[111] Crowley P J D, Datta A, Barbieri M, et al. Tradeoff in simultaneous quantum-limited phase and loss estimation in interferometry[J]. Physical Review A, 2014, 89(2): 023845.

[112] Szczykulska M, Baumgratz T, Datta A. Multi-parameter quantum metrology[J]. Advances in Physics: X, 2016, 1(4): 621-639.

[113] Humphreys P C, Barbieri M, Datta A, et al. Quantum enhanced multiple phase estimation[J]. Physical Review Letters, 2013, 111(7): 070403.

[114] Hong S, Ur Rehman J, Kim Y S, et al. Quantum enhanced multiple-phase estimation with multi-mode N00N states[J]. Nature Communications, 2021, 12: 5211.

[115] Hong S, Rehman J U, Kim Y S, et al. Practical sensitivity bound for multiple phase estimation with multi-mode N00N$N00N$ states[J]. Laser & Photonics Reviews, 2022, 16(9): 2100682.

[116] Polino E, Riva M, Valeri M, et al. Experimental multiphase estimation on a chip[J]. Optica, 2019, 6(3): 288-295.

[117] Valeri M, Polino E, Poderini D, et al. Experimental adaptive Bayesian estimation of multiple phases with limited data[J]. NPJ Quantum Information, 2020, 6: 92.

[118] Zhang Z S, Zhuang Q T. Distributed quantum sensing[J]. Quantum Science and Technology, 2021, 6(4): 043001.

[119] Ge W C, Jacobs K, Eldredge Z, et al. Distributed quantum metrology with linear networks and separable inputs[J]. Physical Review Letters, 2018, 121(4): 043604.

[120] Gross J A, Caves C M. One from many: estimating a function of many parameters[J]. Journal of Physics A: Mathematical and Theoretical, 2021, 54(1): 014001.

[121] Liu L Z, Zhang Y Z, Li Z D, et al. Distributed quantum phase estimation with entangled photons[J]. Nature Photonics, 2021, 15: 137-142.

[122] Guo X S, Breum C R, Borregaard J, et al. Distributed quantum sensing in a continuous-variable entangled network[J]. Nature Physics, 2020, 16: 281-284.

[123] Zhuang Q T, Zhang Z S, Shapiro J H. Distributed quantum sensing using continuous-variable multipartite entanglement[J]. Physical Review A, 2018, 97(3): 032329.

[124] Rubio J, Knott P A, Proctor T J, et al. Quantum sensing networks for the estimation of linear functions[J]. Journal of Physics A: Mathematical and Theoretical, 2020, 53(34): 344001.

[125] Albarelli F, Friel J F, Datta A. Evaluating the Holevo Cramér-Rao bound for multiparameter quantum metrology[J]. Physical Review Letters, 2019, 123(20): 200503.

[126] Matsumoto K. A new approach to the Cramér-Rao-type bound of the pure-state model[J]. Journal of Physics A: Mathematical and General, 2002, 35(13): 3111-3123.

[127] Yang Y X, Chiribella G, Hayashi M. Attaining the ultimate precision limit in quantum state estimation[J]. Communications in Mathematical Physics, 2019, 368(1): 223-293.

[128] Jun S. Explicit formula for the Holevo bound for two-parameter qubit-state estimation problem[J]. Journal of Mathematical Physics, 2016, 57(4): 042201.

[129] Sidhu J S, Ouyang Y K, Campbell E T, et al. Tight bounds on the simultaneous estimation of incompatible parameters[J]. Physical Review X, 2021, 11(1): 011028.

[130] Linden N, Massar S, Popescu S. Purifying noisy entanglement requires collective measurements[J]. Physical Review Letters, 1998, 81(15): 3279-3282.

[131] Yuan Y, Hou Z B, Tang J F, et al. Direct estimation of quantum coherence by collective measurements[J]. NPJ Quantum Information, 2020, 6: 46.

[132] Wu K D, Yuan Y, Xiang G Y, et al. Experimentally reducing the quantum measurement back action in work distributions by a collective measurement[J]. Science Advances, 2019, 5(3): eaav4944.

[133] Conlon L O, Vogl T, Marciniak C D, et al. Approaching optimal entangling collective measurements on quantum computing platforms[J]. Nature Physics, 2023, 19: 351-357.

[134] Cox K C, Greve G P, Weiner J M, et al. Deterministic squeezed states with collective measurements and feedback[J]. Physical Review Letters, 2016, 116(9): 093602.

[135] Conlon L O, Suzuki J, Lam P K, et al. Efficient computation of the Nagaoka-Hayashi bound for multiparameter estimation with separable measurements[J]. NPJ Quantum Information, 2021, 7: 110.

[136] Ragy S, Jarzyna M, Demkowicz-Dobrzański R. Compatibility in multiparameter quantum metrology[J]. Physical Review A, 2016, 94(5): 052108.

[137] Altorio M, Genoni M G, Vidrighin M D, et al. Weak measurements and the joint estimation of phase and phase diffusion[J]. Physical Review A, 2015, 92(3): 032114.

[138] Szczykulska M, Baumgratz T, Datta A. Reaching for the quantum limits in the simultaneous estimation of phase and phase diffusion[J]. Quantum Science and Technology, 2017, 2(4): 044004.

[139] KnyshS I, DurkinG A. Estimation of phase and diffusion: combining quantum statistics and classical noise[EB/OL]. (2013-07-01) [2023-09-08]. https:∥arxiv.org/abs/1307.0470.

[140] Vidrighin M D, Donati G, Genoni M G, et al. Joint estimation of phase and phase diffusion for quantum metrology[J]. Nature Communications, 2014, 5: 3532.

[141] Roccia E, Gianani I, Mancino L, et al. Entangling measurements for multiparameter estimation with two qubits[J]. Quantum Science and Technology, 2018, 3(1): 01LT01.

[142] Qassim H, Miatto F M, Torres J P, et al. Limitations to the determination of a Laguerre-Gauss spectrum via projective, phase-flattening measurement[J]. Journal of the Optical Society of America B, 2014, 31(6): A20-A23.

[143] Bouchard F, Valencia N H, Brandt F, et al. Measuring azimuthal and radial modes of photons[J]. Optics Express, 2018, 26(24): 31925-31941.

[144] Bavaresco J, Herrera Valencia N, Klöckl C, et al. Measurements in two bases are sufficient for certifying high-dimensional entanglement[J]. Nature Physics, 2018, 14: 1032-1037.

[145] Marcikic I, de Riedmatten H, Tittel W, et al. Long-distance teleportation of qubits at telecommunication wavelengths[J]. Nature, 2003, 421(6922): 509-513.

[146] Schreiber A, Gábris A, Rohde P P, et al. A 2D quantum walk simulation of two-particle dynamics[J]. Science, 2012, 336(6077): 55-58.

[147] Lorz L, Meyer-Scott E, Nitsche T, et al. Photonic quantum walks with four-dimensional coins[J]. Physical Review Research, 2019, 1(3): 033036.

[148] Zhong T, Zhou H C, Horansky R D, et al. Photon-efficient quantum key distribution using time-energy entanglement with high-dimensional encoding[J]. New Journal of Physics, 2015, 17(2): 022002.

[149] Nunn J, Wright L J, Söller C, et al. Large-alphabet time-frequency entangled quantum key distribution by means of time-to-frequency conversion[J]. Optics Express, 2013, 21(13): 15959-15973.

[150] Steinlechner F, Ecker S, Fink M, et al. Distribution of high-dimensional entanglement via an intra-city free-space link[J]. Nature Communications, 2017, 8: 15971.

[151] Gianani I, Sbroscia M, Barbieri M. Measuring the time-frequency properties of photon pairs: a short review[J]. AVS Quantum Science, 2020, 2(1): 011701.

[152] Eriksson M, Goldberg A Z, Hiekkamäki M, et al. Sensing rotations with multiplane light conversion[J]. Physical Review Applied, 2023, 20(2): 024052.

[153] Xia B K, Huang J Z, Li H J, et al. Toward incompatible quantum limits on multiparameter estimation[J]. Nature Communications, 2023, 14: 1021.

[154] Tsang M, Nair R, Lu X M. Quantum theory of superresolution for two incoherent optical point sources[J]. Physical Review X, 2016, 6(3): 031033.

[155] Yu Z X, Prasad S. Quantum limited superresolution of an incoherent source pair in three dimensions[J]. Physical Review Letters, 2018, 121(18): 180504.

[156] Napoli C, Piano S, Leach R, et al. Towards superresolution surface metrology: quantum estimation of angular and axial separations[J]. Physical Review Letters, 2019, 122(14): 140505.

[157] Wang B, Xu L, Li J C, et al. Quantum-limited localization and resolution in three dimensions[J]. Photonics Research, 2021, 9(8): 1522-1530.

[158] Prasad S, Yu Z X. Quantum-limited superlocalization and superresolution of a source pair in three dimensions[J]. Physical Review A, 2019, 99(2): 022116.

[159] Řehaček J, Hradil Z, Stoklasa B, et al. Multiparameter quantum metrology of incoherent point sources: towards realistic superresolution[J]. Physical Review A, 2017, 96(6): 062107.

[160] Řeháček J, Hradil Z, Koutný D, et al. Optimal measurements for quantum spatial superresolution[J]. Physical Review A, 2018, 98(1): 012103.

[161] Prasad S. Quantum limited super-resolution of an unequal-brightness source pair in three dimensions[J]. Physica Scripta, 2020, 95(5): 054004.

[162] Bisketzi E, Branford D, Datta A. Quantum limits of localisation microscopy[J]. New Journal of Physics, 2019, 21(12): 123032.

[163] Hradil Z, Řeháček J, Sánchez-Soto L, et al. Quantum Fisher information with coherence[J]. Optica, 2019, 6(11): 1437-1440.

[164] Larson W, Saleh B E A. Resurgence of Rayleigh’s curse in the presence of partial coherence[J]. Optica, 2018, 5(11): 1382-1389.

[165] Tsang M, Nair R. Resurgence of Rayleigh’s curse in the presence of partial coherence: comment[J]. Optica, 2019, 6(4): 400-401.

[166] Larson W, Saleh B E A. Resurgence of Rayleigh’s curse in the presence of partial coherence: reply[J]. Optica, 2019, 6(4): 402-403.

[167] Wang B, Xu L, Xia H K, et al. Quantum-limited resolution of partially coherent sources[J]. Chinese Optics Letters, 2023, 21(4): 042601.

[168] Paúr M, Stoklasa B, Hradil Z, et al. Achieving the ultimate optical resolution[J]. Optica, 2016, 3(10): 1144-1147.

[169] Tham W-K, Ferretti H, Steinberg A M. Beating Rayleigh’s curse by imaging using phase information[J]. Physical Review Letters, 2017, 118(7): 070801.

[170] Parniak M, Borówka S, Boroszko K, et al. Beating the Rayleigh limit using two-photon interference[J]. Physical Review Letters, 2018, 121(25): 250503.

[171] Yang F, Tashchilina A, Moiseev E S, et al. Far-field linear optical superresolution via heterodyne detection in a higher-order local oscillator mode[J]. Optica, 2016, 3(10): 1148-1152.

[172] Tang Z S, Durak K, Ling A. Fault-tolerant and finite-error localization for point emitters within the diffraction limit[J]. Optics Express, 2016, 24(19): 22004.

[173] RouvièreC, RanaD B, GrateauA, et al. Ultra-sensitive separation estimation of optical sources[EB/OL]. (2023-06-20) [2023-08-09]. https:∥arxiv.org/abs/2306.11916.

[174] Boucher P, Fabre C, Labroille G, et al. Spatial optical mode demultiplexing as a practical tool for optimal transverse distance estimation[J]. Optica, 2020, 7(11): 1621-1626.

[175] Hou Z B, Wang R J, Tang J F, et al. Control-enhanced sequential scheme for general quantum parameter estimation at the Heisenberg limit[J]. Physical Review Letters, 2019, 123(4): 040501.

[176] Hou Z B, Tang J F, Chen H Z, et al. Zero-trade-off multiparameter quantum estimation via simultaneously saturating multiple Heisenberg uncertainty relations[J]. Science Advances, 2021, 7(1): eabd2986.

3.2　光学干涉仪中的标准量子极限与海森堡极限

3.3　存在损耗的光学干涉仪中相位测量的量子极限

3.4　多参数量子精密测量

3.5　光量子精密测量的其他应用

4　结语

王犇, 张利剑. 光量子精密测量研究进展（特邀）[J]. 中国激光, 2024, 51(1): 0112001. Ben Wang, Lijian Zhang. Progress in Photonics Quantum Metrology (Invited)[J]. Chinese Journal of Lasers, 2024, 51(1): 0112001.

光量子精密测量研究进展（特邀）下载： 781次创刊五十周年特邀

1　引言

2　量子精密测量的基本原理

2.1　量子精密测量的一般过程

图 1. 量子精密测量的一般过程

Fig. 1. General process of quantum metrology

2.2　量子参数估计理论

2.3　基于量子资源的量子增强精密测量

图 2. 针对未知参数测量的4种不同的并行方案。（a）经典-经典方案；（b）经典-量子方案；（c）量子-经典方案；（d）量子-量子方案

Fig. 2. Four different parallel strategies for estimation of unknown parameter. (a) Classical-classical strategy; (b) classical-quantum strategy; (c) quantum-classical strategy; (d) quantum-quantum strategy

表 1. 五种关键指标的相互关系

Table 1. Interrelationship of five key quantities

图 3. 串行方案

Fig. 3. Sequential strategy

3　光量子精密测量及其应用

3.1　光学干涉仪

图 4. Mach-Zehnder干涉仪的一般结构

Fig. 4. General construction of Mach-Zehnder interferometer

3.2　光学干涉仪中的标准量子极限与海森堡极限

图 5. Hong-Ou-Mandel干涉的基本原理

Fig. 5. Fundamental principle of Hong-Ou-Mandel interference

图 6. 不同类型的干涉仪结构。（a）Michelson干涉仪；（b）Sagnac干涉仪

Fig. 6. Structures of different types of interferometers. (a) Michelson interferometer; (b) Sagnac interferometer

3.3　存在损耗的光学干涉仪中相位测量的量子极限

图 7. 存在损耗的光学干涉仪，加载相位的位置透过率为 $η$

Fig. 7. Lossy optical interferometer with transmissivity $η$ of encoding phase

3.4　多参数量子精密测量

图 8. 多相位估计示意图

Fig. 8. Schematic of multiple phases estimation

3.5　光量子精密测量的其他应用

图 9. 经典成像系统中的Rayleigh判据

Fig. 9. Rayleigh criterion in classical imaging systems

4　结语

Article Outline

关于本站 Cookie 的使用提示

全站搜索

光量子精密测量研究进展（特邀） 下载： 781次创刊五十周年特邀

1 引言

2 量子精密测量的基本原理

2.1 量子精密测量的一般过程

图 1. 量子精密测量的一般过程

Fig. 1. General process of quantum metrology

2.2 量子参数估计理论

2.3 基于量子资源的量子增强精密测量

图 2. 针对未知参数测量的4种不同的并行方案。（a）经典-经典方案；（b）经典-量子方案；（c）量子-经典方案；（d）量子-量子方案

Fig. 2. Four different parallel strategies for estimation of unknown parameter. (a) Classical-classical strategy; (b) classical-quantum strategy; (c) quantum-classical strategy; (d) quantum-quantum strategy

表 1. 五种关键指标的相互关系

Table 1. Interrelationship of five key quantities

图 3. 串行方案

Fig. 3. Sequential strategy

3 光量子精密测量及其应用

3.1 光学干涉仪

图 4. Mach-Zehnder干涉仪的一般结构

Fig. 4. General construction of Mach-Zehnder interferometer

3.2 光学干涉仪中的标准量子极限与海森堡极限

图 5. Hong-Ou-Mandel干涉的基本原理

Fig. 5. Fundamental principle of Hong-Ou-Mandel interference

图 6. 不同类型的干涉仪结构。（a）Michelson干涉仪；（b）Sagnac干涉仪

Fig. 6. Structures of different types of interferometers. (a) Michelson interferometer; (b) Sagnac interferometer

3.3 存在损耗的光学干涉仪中相位测量的量子极限

图 7. 存在损耗的光学干涉仪，加载相位的位置透过率为η

Fig. 7. Lossy optical interferometer with transmissivity η of encoding phase

3.4 多参数量子精密测量

图 8. 多相位估计示意图

Fig. 8. Schematic of multiple phases estimation

3.5 光量子精密测量的其他应用

图 9. 经典成像系统中的Rayleigh判据

Fig. 9. Rayleigh criterion in classical imaging systems

4 结语

Article Outline

相关论文

相关资讯

关于本站 Cookie 的使用提示

全站搜索

光量子精密测量研究进展（特邀）下载： 781次创刊五十周年特邀

1　引言

2　量子精密测量的基本原理

2.1　量子精密测量的一般过程

2.2　量子参数估计理论

2.3　基于量子资源的量子增强精密测量

3　光量子精密测量及其应用

3.1　光学干涉仪

3.2　光学干涉仪中的标准量子极限与海森堡极限

3.3　存在损耗的光学干涉仪中相位测量的量子极限

图 7. 存在损耗的光学干涉仪，加载相位的位置透过率为 $η$

Fig. 7. Lossy optical interferometer with transmissivity $η$ of encoding phase

3.4　多参数量子精密测量

3.5　光量子精密测量的其他应用

4　结语