1 Introduction

Imaging through multimode fibers (MMFs) of tens to hundreds of micrometers enables high-resolution imaging by a hair-thin instrument. It provides minimally invasive high-resolution imaging for locations deep inside living organisms1 without traumatic tissue slices.2 Its broad applications include in vivo endoscopes,3^–5 optical tweezers over cellular area,6^,7 and remote time-of-flight 3D depth sensing.8

MMF imaging is achieved by exploiting the property of transmission matrix (TM). With the TM, one can collect the feedback signal after rapidly scanning foci on the sample5^,9 or directly inverse the scattering process.10^,11 However, the calibration of TM requires measuring the transmitted complex fields after sending probing incident complex fields. With both amplitude and phase, the complex fields cannot be measured directly by a camera. Conventionally, external reference methods12^–14 build a complicated experimental setup to interferometrically measure the transmitted complex field with an external reference beam. These methods suffer from phase instability of the reference beam, easily caused by mechanical variation and thermal drift. The internal reference methods9^,15^,16 set parts of the modulation modes as an internal reference. It reduces the number of effective modulation modes and uses speckle reference, which contains dark reference points.1^,16 Its retrieved TM has the phase offset error, excluding applications that require 3D focusing.6 Therefore, it is desirable to develop a simple and stable method to measure the full TM in MMF imaging.

The reference-less TM retrieval methods computationally recover the TM from the intensity images of the transmitted complex fields measured by a reference-less experimental setup17 [Fig. 1(a)]. This provides a promising solution to robustly measure the TM in MMF imaging. However, the application of reference-less TM retrieval in MMF imaging still faces issues of long computational time and phase offset error. Algorithms based on the Bayesian approach,17^,18 Gerchberg–Saxton,19 semi-definite programming,20 Kalman filter,21 prVAMP,22 and reweighted amplitude flow23 have been proposed for reference-less TM retrieval. When the TM is large, the computational time of these algorithms could be hours.19^,22 Another issue is that the TM acquired by the reference-less TM retrieval has the error of phase offset.6 The reference-less TM retrieval only maps the incident fields with the intensity images at one fixed camera plane, causing the loss of relative phase information between different pixels. The transmitted complex field predicted using the acquired TM with the phase offset error has correct amplitudes but wrong phases. It causes failure of generating 3D light patterns, such as 3D foci or light sheet, which is essential in volumetric imaging24 and light-sheet imaging by MMF.25

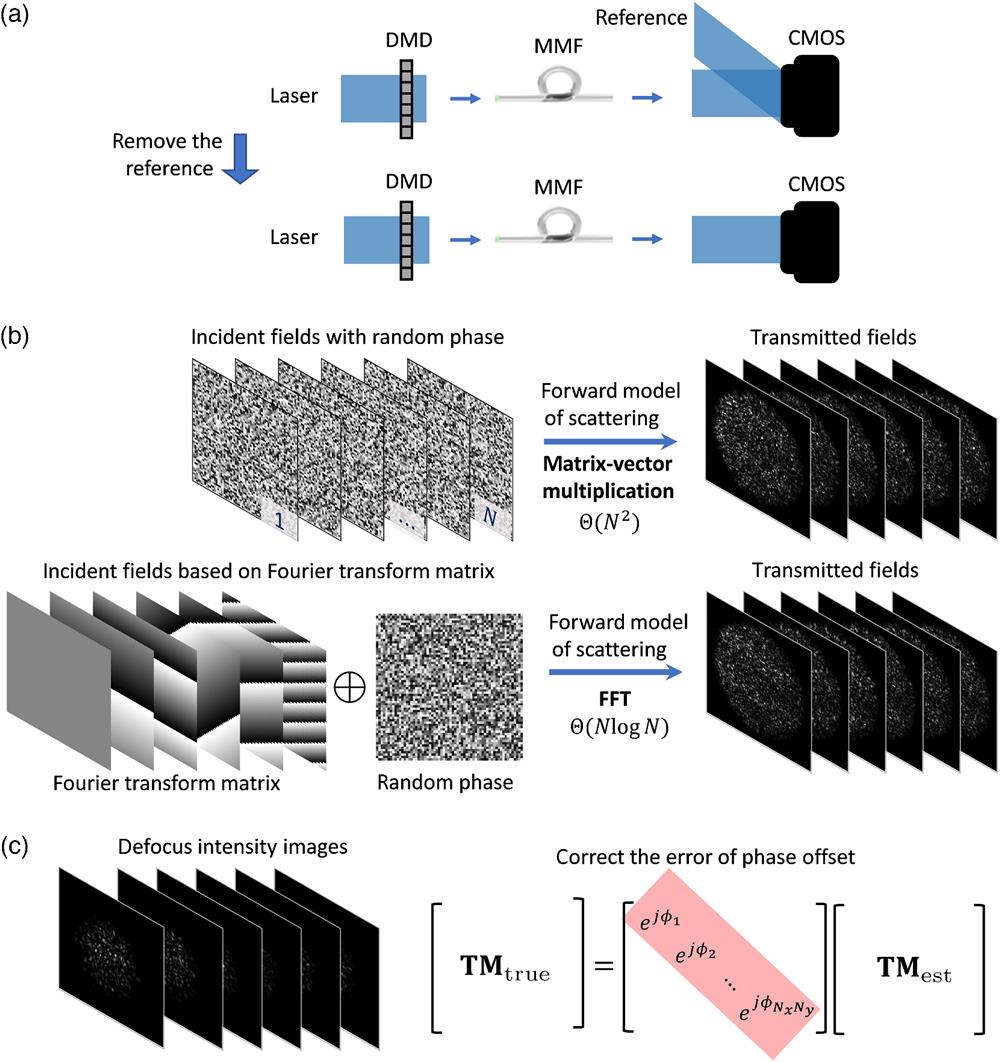
Fig. 1. TM retrieval with fast Fourier transform (FFT) and phase correction from intensity measurements without reference. (a) Comparison of data acquisition between the reference-less methods and the reference-based methods. The reference-based methods measure the complex fields with a reference beam, while the reference-less methods take only intensity without any reference, leading to a simpler and more stable experimental setup. (b) Computational efficiency improvement using FFT. In the conventional methods, the incident fields are directly generated with random phases, and the forward model of scattering has to be computed by matrix–vector multiplication. Our method designs the incident fields based on the Fourier transform matrix. Thus the forward model of scattering can be computed by FFT, which significantly improves computational efficiency. It also allows the inverse algorithm of TM retrieval to be implemented with FFT. (c) Correction of the error of phase offset using defocus intensity images. The estimated TM from the intensity images measured at one defocus plane has the error of phase offset. Our algorithm corrects the phase errors using the defocus intensity images.

下载图片 查看所有图片

Here we propose a fast and phase-offset-error-free reference-less TM retrieval method and demonstrate with experimental setup of MMF imaging. First, we design the probing incident complex fields with Fourier transform matrix and develop a nonlinear optimization algorithm to solve the TM from the intensity-only measurements. Compared to the scheme of random probing incident fields,19^–21 our scheme allows the inverse algorithm to be implemented with FFT [Fig. 1(b)], which greatly reduces the computational complexity. Second, our method measures a set of intensity images at a defocus plane from the distal end of the MMF and develops an algorithm to recover the phase offset from the defocus intensity images [Fig. 1(c)]. The simulation shows the TM retrieval algorithm with FFT has a 1200× speedup in computational time compared to that of the TM retrieval algorithm without FFT. The proposed TM retrieval method recovers TM for an MMF of 0.22 NA and 50μm diameter with 112.9 s. We build the experimental setup with MMF and verify the proposed methods by evaluating the foci in both 2D and 3D.

In addition to MMF imaging, TM measurement is important to applications that require characterizing the scattering property. The applications range from imaging through scattering media or tissue,26 high-capacity communication through optical fiber,27 optical computing systems,28^,29 quantum networks,30^,31 and thin-lens imaging by nano-optics,32 to holographic display with scattering media.33 As an alternative to the interferometry-based external reference methods, reference-less TM retrieval provides a simple and robust way to acquire the TM in these applications. However, the issues of long computational time and phase offset error commonly exist, especially when the TM is large. Our method may be adapted to solve the issues of reference-less TM retrieval for these applications.

2 Methods

2.1 Experimental Setup

The reference-less experimental setup is shown in Fig. 2. An MMF of 0.22 NA and 50μm diameter (ChunHui CCS50/125H-F-F-1) is used. It aims to generate incident complex fields impinging on the proximal end of the MMF and measure the intensity images of the transmitted complex fields of the MMF. A collimated laser of 488 nm (Precilasers SF-488-0.5-CW) is directed on a digital micromirror device (DMD, Vialux v9501). It displays the binary hologram obtained by the Lee hologram method.34 A set of half-wave plates and quarter-wave plates interposed between the DMD and the polarization beam splitter PBS1 turns the light reflected from the DMD into circular polarized light. The s and p lights from PBS1 pass through the mirrors M2 and M3 separately, combine by the polarization beam splitter PBS2, and impinge on the iris after being Fourier-transformed by lens L3. The s and p lights are programmed with different carrier frequencies on the binary hologram, which determines the locations the −1st diffraction order on the iris. Tuning M2 and M3 shifts the −1st diffraction order of the s and p lights through the pinhole on the iris. The telescope system formed by lens L4 and the objective lens OBJ1 (Olympus 10× NA 0.25) focuses the light emitted from the iris on the proximal end of the MMF. Thus the incident complex fields with desired phases are generated for both polarizations. Dual polarization modulation allows better control of the transmitted complex fields, resulting in scanning foci of improved quality for MMF imaging.13

Fig. 2. Experimental setup. The light-modulation module on the left of the MMF simultaneously generates the incident complex fields for both polarizations, while the calibration module on the right measures the intensity distribution of the transmitted complex fields. The abbreviations are defined as follows: L1 to L5, lens; DMD, digital micromirror device; M1 to M3, mirror; HWP, half-wave plate; QWP, quarter-wave plate; PBS1-2, polarization beam splitter; OBJ1-2, objective lens; LP, linear polarizer; CMOS, complementary metal oxide semiconductor.

下载图片 查看所有图片

The 4f system formed by the objective lens OBJ2 (Olympus 20× NA 0.25) and the lens L5 magnifies the transmitted complex field. A CMOS camera (Basler acA720-520um) captures the intensity image after the light passes through a linear polarizer. The synchronization of the DMD (refresh rate of 16.7 kHz) and the CMOS camera enables measuring the intensity images at a high frame rate up to 525frame/s. By moving the OBJ2 with a stage (Thorlabs CT1P), the CMOS camera captures the intensity images at a defocus plane.

2.2 TM Retrieval

Our method recovers the TM from the intensity images measured from the reference-less experimental setup in Fig. 2. The data-acquisition measures the intensity images of the transmitted complex fields for TM retrieval after sending in the phase-only incident complex fields generated by modulating the DMD. Next, we develop an efficient nonlinear optimization algorithm to recover the TM from the intensity measurements.

2.2.1 Pixel-wise inverse problem

The intensity images are denoted as In(x,y), where n=1,…,N, N is the total number of the measured intensity images, and x,y are the spatial coordinates. Each image contains Nx×Ny pixels. The incident complex field is raster-scanned into a vector ejθn, which has Nk modulation modes for both polarizations. The forward model of the intensity measurement is written as In=|Tejθn|2,(1)where In is a vector raster-scanned from In(x,y), T is the transmission matrix (Nx*Ny×Nk), and |·| takes absolute square of the complex numbers inside.

The optimization problem of retrieving the TM from the intensity images is formulated as minT∑n‖In−|Tejθn|2‖22,(2)where |·|22 is the squared L2 norm of the vector inside. The cost function is the sum of the squared error between the intensity measurements and the intensity predicted by the forward model. The optimization problem solves T by minimizing the cost function.

The large number of unknown in T makes the optimization problem in Eq. (2) difficult to solve directly. However, it can be broken down into Nx*Ny smaller optimization problems. Each problem is formulated based on the intensity measurement at one single pixel, mintkf(tk)=‖Ik−|Qtk|2‖22,(3)where Ik=[I1kI2k⋮INk],Q=[ejθ1Tejθ2T⋮ejθNT].(4)

Here the column vector tk is the transpose of the kth row of T, Ink is the kth element of In, T denotes transpose, and k=1,…,Nx*Ny. The vector Ik contains all of the measurements at the same pixel indexed by k on the intensity images. The matrix Q is the so-called probing matrix; each row of Q is one of the incident fields. Each optimization problem recovers one row of T from the measurements at the corresponding pixel. Thus the whole TM can be recovered by solving these small pixel-wise optimization problems independently.

2.2.2 Inverse algorithm with a designed probing matrix

Conventional reference-less TM retrieval methods19^–21 set the phases of the probing matrix Q as random numbers. It means that the incident fields are modulated with random phases in these methods. By contrast, our method designs the matrix Q with Fourier transform matrix, Q=[Kdiag(ejψ1)Kdiag(ejψ2)⋮Kdiag(ejψM)],(5)where K is the Fourier transform matrix, ejψm is a Nk by 1 column vector with its phase set as random numbers, diag(ejψm) is a diagonal matrix with its diagonal entries from ejψm, and m=1,…,M. The incident complex field has Nkx×Nky modulation modes for each polarization, so we have Nk=2Nkx*Nky. The total number of measured intensity images is N=M*Nk, which is M-fold of the size of the unknown complex variable, tk. We set M≥3, since the complex variable in the inverse problem contains both real and imaginary parts. The matrix Q consists of M square matrix in the form of Kdiag(ejψm), where K is the 2D Fourier transform matrix for Nkx×2Nky matrix. Since K is a pure phase matrix, the probing matrix Q remains as pure phase. So it can be loaded into the phase modulator to generate desired incident fields. When the phases of the probing matrix Q are random,19^–21 the multiplication of Q with a vector has to be computed with matrix–vector multiplication. Our method designs the probing matrix Q with the Fourier transform matrix, so the matrix–vector multiplication related to Q can be computed with FFT or inverse FFT (for its complex transpose QH). This advantage can be exploited to accelerate the algorithm for TM retrieval.

The optimization problem in Eq. (3) recovers the complex unknown from the intensity measurement and can be viewed as a phase-retrieval problem. We solve the optimization problem using the nonlinear optimization phase-retrieval method,35 which has been developed for phase retrieval from defocus intensity images. It derives the derivative for the complex variable and adopts the limited memory Broyden–Fletcher–Goldfarb—Shanno (L-BFGS) method36^,37 to solve the phase-retrieval problem. The optimization is initialized by backpropagation, $$\begin{gathered} t0k=(QHQ)−1QHIk \\ =1MQHIk, \end{gathered}$$(6)where Ik takes the element-wise square root of the vector Ik, and H denotes the complex transpose. Since KH is the inverse Fourier transform matrix, the matrix–vector multiplication in QHIk can be computed with FFT. We derive the first derivative of f(tk) with respect to tk as (more details in Appendix A) ∂f∂tkH=−4QHdiag(Qtk)(Ik−|Qtk|2),(7)∂fH∂tk=∂fT∂txk+j∂fT∂tyk,(8)where txk and tyk are the real and imaginary parts of tk. The matrix–vector multiplication related to Q in Eq. (7) can be computed with FFT.

The procedure of the algorithm to solve the optimization problem in Eq. (3) is summarized in Algorithm 1. The algorithm has inputs of the intensity measurements at kth pixel Ik and random phase vectors for the probing matrix ejψm. It recovers one row of the TM, tk. The estimation is initialized by Eq. (6). After obtaining the error [Eq. (3)] and gradient [Eq. (7)], the algorithm updates the estimate of tk iteratively according to the L-BFGS method. The update iteration stops when a preset maximum iteration number is reached. The matrix–vector multiplication related to Q in Eqs. (3), (6), and (7) can be efficiently computed with FFT, reducing the computational complexity from Θ(NNk) to Θ(NlogNk). It also has the benefit of memory efficiency, since there is no need to explicitly store the big matrix Q when solving the inverse problem.

2.2.3 Recovery of the whole TM

One may apply the method in Algorithm 1 on all the Nx*Ny optimization problems in the form of Eq. (3) and recover the entire TM. However, this could be unnecessary due to the physical properties of the MMF. There is negligible transmitted light on the pixels outside the distal end of the fiber. The complex field at the distal end of the MMF has highest frequency limited by NA/λ, where NA is the numerical aperture of the MMF, and λ is the wavelength. Therefore, we design a preprocessing procedure to reduce the number of effective pixels, which in turn brings down the number of optimization problems. First, we half-sample the measured intensity images by only keeping the pixels of the odd indices in the images. Without loss of generality, we assume that the pixel size of the measured intensity images, psintensity, meets the Nyquist sampling theory, psintensity≤λ/4NA.(9)

So, the pixel size of the half-sampled images has psfield=psintensity*2. It meets the sampling requirement of the transmitted complex field, psfield≤λ/2NA.(10)The half-sample step reduces the number of the optimization problems by a factor of 4. Second, from the half-sampled intensity images, we obtain a binary fiber mask, which masks out the MMF region. The pixels within the distal end of the MMF have a value of 1, while the pixels outside of the MMF have a value of 0. For the pixels in the zero-value region, the vectors tk are directly set to zeros, without solving the optimization problem of Eq. (3). At the end, our TM retrieval method only solves the optimization problems from the half-sampled intensity images for the pixels inside the distal end of the fiber. Thus the number of optimization problems is greatly reduced.

The full procedure of the TM retrieval method is summarized in Fig. 3. The optimization problems of Eq. (3) are independent. So our method solves these optimization problems in parallel with a computer of multiple CPU cores, which can be easily implemented by parfor on MATLAB.

Fig. 3. Full procedure of the TM retrieval method. The intensity images are measured at one fixed camera plane.

下载图片 查看所有图片

2.3 Phase Correction

The optimization problem in Eq. (3) has the issue of phase ambiguity. It means multiplying an optimal solution of the optimization problem with an arbitrary phase term, ejϕ0 still gives an optimal solution. The phase ambiguity leads to the error of phase offset between the estimated TM and the true TM. It has Ttrue=diag(ejϕ)Test,(11)where Ttrue is the true TM, Test is the estimated TM, and the vector ejϕ is the phase offset (size Nxhalf*Nyhalf×1). Note that Nxhalf and Nyhalf are the size of the half-sampled intensity image, due to the preprocessing step in Fig. 3.

In order to generate foci at the measurement plane of the intensity images, the incident complex fields are modulated with phases of the conjugate of the estimated TM row by row. The phase offset error of Test still allows pixel-wise constructive interference, resulting in the generation of 2D scanning foci at the measurement plane. However, to generate foci at other focal planes, the incident complex fields are modulated with a free-space-propagated version of Test. The phase offset error causes random error in the propagated TM, leading to failure of generating 3D distributed foci at other focal planes.

To solve the issue of phase ambiguity, we propose a phase correction method after Test has been obtained by the TM retrieval method in Fig. 3. Our method corrects the phase offset using multiple defocus intensity images. After applying random phases to modulate the incident fields, our method measures intensity images at a defocus plane that is zd away from the distal end of the MMF (z=0). The defocus intensity images results from free-space propagation of the transmitted complex field at the distal end of the fiber. These defocus intensity images capture the phase information of the transmitted complex fields. Therefore, it is possible to invert the phase offset of the estimated TM from the defocus intensity images.

We build the forward model for the inverse problem of the phase offset recovery from the defocus intensity images. The defocus intensity images are denoted with Ind(x,y,zd), where nd=1,…,Nd. Each intensity image has a size of Nx×Ny with pixel size of psintensity. From Eq. (11), the transmitted complex field at the distal end of the MMF can be expressed as cnd=diag(Testejθnd)ejϕ,(12)where ejθnd is raster-scanned from the corresponding incident complex field of the defocus intensity image, Ind(x,y,zd). Note that the transmitted complex field predicted by the estimated TM has a size of Nxhalf×Nyhalf with pixel size of psfield. The vector cnd is the raster-scanned form of the transmitted complex field.

The complex field at the defocus plane and the transmitted complex field at the distal end of the MMF are related by defocus propagation. The forward model of the defocus intensity can be expressed as Ind=|K2HPdiag(h)K1diag(Testejθnd)ejϕ|2,(13)where the vector Ind is raster-scanned from Ind(x,y,zd), K1 is the Fourier transform matrix for the Nxhalf×Nyhalf matrix, h is the defocus propagation kernel (more in Appendix B), P is for zero padding in the frequency domain, and K2H is the inverse Fourier transform matrix for the Nx×Ny matrix. The measured intensity has a size of Nx×Ny, whereas the transmitted complex field has a size of Nxhalf×Nyhalf. The zero padding here adds zeros in the frequency domain, which results in doubling the number of pixels in both dimensions. It has the effect of reversing the half-sample step in Fig. 3.

The optimization problem of solving the phase offset from the defocus intensity images is formulated as minϕg(ϕ)=∑nd‖Ind−|Andejϕ|2‖22,(14)where And=K2HPdiag(h)K1diag(Testejθnd). The cost function is defined as the squared error between the measured defocus intensity and the intensity predicted with the phase offset.

The first derivative of the optimization problem in Eq. (14) is derived as ∂g∂ϕH=∑ndreal[−4diag(−je−jϕ)AndHdiag(Andejϕ)⁢(Ind−|Andejϕ|2)].(15)

More details can be found in Appendix C. The matrix–vector multiplication related to And in Eqs. (14) and (15) can be computed with FFT, without explicitly forming the big matrices. With the cost function in Eq. (14) and the first derivative in Eq. (15), our method uses the L-BFGS method36^,37 to recover the phase offset from the defocus intensity images.

3 Results for TM Retrieval Using Intensity Images at One Measurement Plane

In this section, we verify the TM retrieval algorithm using intensity images measured at one fixed plane (Fig. 3) by both simulations and experiments. In the simulation, a TM of size 9216×8192 was used to generate simulated data. The TM had been measured experimentally by the off-axis holography method13 with an external reference beam, for an MMF of 0.22 NA and 50μm diameter. The incident complex fields had 64×64 phase modulation modes for each polarization. The matrix K in the probing matrix was set as the Fourier transform matrix for a 64×128 matrix. The transmitted complex fields at the distal end were sampled with 96×96pixels. We simulated seven datasets with M=3 to 9, where M is the total number of Kdiag(ejψm) in Eq. (5).

We ran the TM retrieval algorithm on each of the simulated datasets. The entire TM was recovered by applying the method in Algorithm 1 on all of the 9216 pixels, without the preprocessing step in Fig. 3. For each dataset, the optimization problems were solved in a parallel manner on a computer with 32 CPU cores (Intel Xeon Gold 5218 2.3 GHz). For the dataset of M=8, it took 376.4 s to retrieve the entire TM of size 9216×8192. Figure 4 compares the error of the recovered TM using the datasets of different measurement sizes. It shows the root-mean-square error (RMSE) of both amplitude [Fig. 4(a)] and phase [Fig. 4(b)] of the recovered TM. Each row of the recovered TM is compared with its true value, and the errors of all of the 9216 rows are organized in 96×96 grids, which are shown in Fig. 4. The phase error is obtained by subtracting the phase of each row of the recovered TM with the true values after removing the constant phase offset [Eq. (11)]. For M=3, most rows of the recovered TM have large errors. For M=4 to 6, a few of the rows of the recovered TM have large errors; there are random bright spots (meaning large errors) in the images at the top row of Figs. 4(a) and 4(b). However, these speckles disappear as M increases. The error of the recovered TM becomes negligibly small for M=7 to 9. The plots on the bottom left on Figs. 4(a) and 4(b) show the RMSE of both amplitude and phase of the recovered TM converge to zero for M=7 to 9. The simulation demonstrates the proposed TM retrieval method is able to efficiently recover the TM from the intensity images measured at one imaging plane with negligible errors.

Fig. 4. Error of recovered TM using the simulated datasets. (a) Normalized amplitude error of the recovered TM for datasets of different M. The errors of M=3 to 5 share the same color bar on the top right, while the errors of other data sets share the color bar on the bottom. The plot at the bottom left shows the RMSE of amplitude of the recovered TM. (b) Phase error of the recovered TM for data sets of different M. The errors of M=3 to 5 share the top right color bar, while the errors of the other data sets share the bottom color bar. The plot shows the RMSE of phase of the recovered TM for different M.

下载图片 查看所有图片

Table 1 shows the speedup of computational time by the proposed TM retrieval with FFT. The central 32×32pixels of the 96×96pixels of the dataset of M=8 were used to access the computational time of the TM retrieval algorithms. The TM retrieval algorithm without FFT replaces the FFT in Algorithm 1 with matrix–vector multiplication. The TM retrieval algorithm without FFT recovers the 1024×8192 TM with 43,664.1 s (12.1 h). However, the proposed TM retrieval algorithm implemented with FFT recovers the same-sized TM with 35.4 s. For the proposed algorithm, each row of the TM takes 0.035 s on average. Using FFT, the proposed TM retrieval algorithm achieves 1200× speedup.

In the experiment, we used an MMF of 0.22 NA and 50μm diameter. The illumination was laser of 488 nm. The DMD achieved 64×64 phase modulation for each polarization, resulting in 8192 modes in total. We tested the TM retrieval algorithm for the cases of M=4 to 8. Each case followed the procedure in Fig. 3 to recover the TM. For each case, we generated the probing matrix with random phase vectors and Fourier transform matrix by Eq. (5). The matrix K was set as the Fourier transform matrix for a 64×128 matrix. The phase of the probing matrix was loaded into the DMD, and a series of M*8192 images [Fig. 5(a)] were measured. Each image has 128×128pixels, with a pixel size of 0.47μm. The preprocessing step half-sampled the measured images and obtained images of 64×64 [Fig. 5(b)]. From the sum image of the preprocessed images, we calculated the fiber mask [Fig. 5(c)], which covers 99.9% of the total energy. The white region of the mask indicates the distal end of the MMF fiber. Only for the pixels inside the fiber mask, the TM was retrieved by Algorithm 1 from the preprocessed images of each dataset.

Fig. 5. Comparison of the foci generated using the recovered TM and the TM measured by the off-axis holography method. (a) Series of measured speckle intensity images. We give an example of the measured images using the data set of M=7. (b) Prepossessing step half-samples the measured 128×128 images into 64×64 images. (c) Binary fiber mask (M=7). The white region of the mask indicates the distal end of the MMF fiber. (d) Recovered PR of M=4 to 8 and the recovered PR of the holography method. For the cases of M=7 and 8, the PR of the foci is near to that of the case of holography. The number inside the image is the average of the top 2000 PR. (e) Histogram of the top 2000 PR. The TM of M=8 has 1424 foci that have PRs higher than 0.60, whereas the holography method has 1266 foci above 0.60. (f) Sum projection of selected foci.

下载图片 查看所有图片

Here we give an example of the case of M=7. The probing matrix has a size of 57,344×8192. The preprocessed intensity images contain 57,344 images of size 64×64. The number of pixels inside the white region of the fiber mask is 2286, so the retrieved TM has size of 2286×8192. For each selected pixel, an optimization problem in the form of Eq. (3) is formulated; it has inputs of the intensity measurement at the corresponding pixel (a vector of 57,344×1) and the random phase vectors used to generate the probing matrix. All these 2286 optimization problems were solved in parallel on the computer with 32 CPU cores. For the case of M=7, the computer takes 112.9 s to solve the optimization problems in TM retrieval.

The accuracy of the recovered TM was tested by the ability to generate foci at the measurement plane. After the TM was retrieved for each case, we uploaded the phase of the conjugate complex of the recovered TM into the phase modulator, sequentially modulated the incident field with its phase row by row, and measured the generated intensity images. When the displayed phase of a row of the retrieved TM matches with the true TM of the imaging system, a focus is generated at the camera. In order to evaluate the quality of the focus, we measured two images (128×128pixels) for each focus with an exposure time of 70 and 1400μs (over exposure at the focus) and calculated the power ratio (PR) of the focus by combining these two images. The PR is the ratio of the signal to the total energy.1 The signal is the sum of the 7×7pixels near the peak of the focus using the 70μs image, while the total energy is the sum of the signal and the background (outside the 7×7pixels), which is calculated using the 1400μs image. The PR reflects the quality of the focus, and hence experimentally shows the correctness of the retrieved TM. We measured a TM by the off-axis holography method with an external reference beam and acquired the corresponding focal images. The result by the holography method acts as a reference for our method. Figure 5(d) shows the PR of the foci of cases of different M and the holography method. For the cases M=4 to 6, there are several foci that have a low PR. However, for the cases of M=7,8, the overall quality of the foci is near to that of the holography method. The average PR of the case of M=8 is 0.64, which is slightly lower than that of the case of holography (0.651). Figures 5(e) and 5(f) further compare the cases of M=8 and holography by showing the distribution of the PR and a sum projection of several selected foci. The TM retrieval method by M=8 has more foci of PR above 0.60 than that of the holography method. And hence, the accuracy of the TM recovered by our proposed reference-less method is validated by comparing with the holography method.

4 Results for TM Retrieval with Phase Correction

In this section, we validate the TM retrieval algorithm with phase correction. For simulation, we used a simulated TM of size 16,384×9216 for an MMF with 0.22 NA and 100μm diameter, generated by solving Maxwell’s equations.38 The transmitted complex fields of the MMF are sampled by 128×128 grids with a pixel size of 1.1667μm, and the wavelength of illumination is 532 nm. We designed a probing matrix with 2D Fourier transform matrix for a 96×96 matrix and M=9. A series of 82,944 images of size 128×128 were generated at the distal end of the fiber (z=0μm). Then we simulated 50 defocus images [Fig. 6(a)] at zd=50μm away from the distal end of the MMF. Each image has 256×256pixels with a pixel size of 0.5833μm. The incident complex fields were obtained by 50 random phases, and the defocus intensity images were generated by Eq. (13).

Fig. 6. Simulation for the TM retrieval algorithm with phase correction. (a) Defocus intensity images measured for the phase correction. (b) Recovered phase offset by the phase correction algorithm. (c) Amplitude error and phase error of the recovered TM with phase correction. The amplitude error is obtained by subtracting the amplitudes of the corrected TM with the true TM. The phase error is the difference between the phases of the corrected TM and the true TM after removing a constant phase offset. The RMSE of all rows of the TM are organized in 128×128 grids, corresponding to the distal end of the MMF. The numbers inside the images are the RMSE over all rows.

下载图片 查看所有图片

We first followed the preprocessing step and the optimization step of the procedure in Fig. 3 to recover the TM from the simulated data. In the preprocessing step, the half-sample step was not performed, since the pixel size already meets the sampling requirement of the complex field. A fiber mask was generated, resulting 6668 selected pixels inside the white region. For the selected pixels, the optimization problems in the form of Eq. (3) were solved, and the rows of the recovered TM corresponding to the black region in the mask were set to zeros. Thus a recovered TM was obtained but has the error of phase offset, since the measured intensity images were at one fixed plane. Next, the phase offset was solved from the defocus images and the recovered TM by the phase-correction algorithm. The computational time for the TM retrieval and the phase correction was 332.9 and 85.2 s, respectively. Figure 6(b) shows the recovered phase offset by the algorithm. Finally, we compensated the phase offset error of the recovered TM using the recovered phase. The amplitude and phase RMSE of the recovered TM with phase correction is 6.4×10−10 and 3.9×10−5, respectively. The error between the recovered TM with phase correction and the true TM is small, as shown in Fig. 6(c).

We further validated the TM algorithm with phase correction by experimentally displaying 3D foci. In the experiment, we used an MMF of 50μm diameter and 0.22 NA, and illumination wavelength of 488 nm. The phase modulation on DMD had 64×64 modes for each polarization. We designed a probing matrix using Fourier transform matrix for a 64×128 matrix, and M=8. After modulating the DMD with the phase of the probing matrix, we sequentially measured 65,536 intensity images at the distal end of the MMF (z=0μm). Each image has 192×192 pixels with a pixel size of 0.4182μm. In order to correct the phase offset, we measured 50 images of 192×192 at 40μm away from the distal end [Fig. 7(a)]. The defocus images were measured after applying 50 random phases on the phase modulator.

Fig. 7. Correction of the phase offset error in the TM using defocus intensity images. (a) Stack of defocus images. (b) Recovered phase offset by the phase correction algorithm. (c) The intensity images generated using the TM with the error of phase offset and the recovered TM with phase correction. The top row shows the measured intensity images using the TM with the error of phase offset. The foci scattered at large defocus distances. The bottom row shows the measured intensity images using the recovered TM with phase correction. The top row images of −40, −60, −80, and −100μm share the top color bar, whereas the other images share the bottom color bar.

下载图片 查看所有图片

We first recovered a TM from the intensity images measured at z=0μm by the proposed method in Fig. 3. In the preprocessing step, we half-sampled the images to a size of 96×96 and generated a fiber mask, which has 3015 pixels inside the white region of the mask. By solving the optimization problems, the TM retrieval algorithm obtained a TM with the error of the phase offset. Next, the algorithm of phase correction recovered the phase offset [Fig. 7(b)] from the defocus intensity images. The recovered phase offset was used to correct the error of phase offset in the recovered TM. The computational time for the algorithm of TM retrieval and the algorithm of phase correction were 199.3 and 20.6 s, respectively.

We tested the recovered TM by generating 3D foci on the imaging system. The propagated TM at a defocus distance could be obtained by adding the recovered TM at z=0μm with a free-space defocus propagation. We generated the two sets of propagated TMs at z=0,−20,−40,−60,−80, and −100μm, using the recovered TM with the error of phase offset and the recovered TM with phase correction. We sequentially applied the phases of complex conjugate of the propagated TM to the DMD and measured intensity images at the corresponding defocus distances. Figure 7(c) compares the intensity images measured at different defocus distances for the foci at the center of the images. For the case of the TM with phase error, the focus could be seen at the image center for z=0μm, but it quickly scattered into random patterns at other defocus distances [top row of Fig. 7(c)]. The phase offset error causes the failure in generating 3D foci. In contrast, the propagated TM generated using the recovered TM with phase correction successfully generated the foci at defocus distances [bottom row of Fig. 7(c)]. As the defocus distances increase from 0 to 100μm, the PRs of the foci reduce from 0.60 to 0.51. The decrease of focus brightness could be caused by the defocus propagation. It adds more correlation for the rows of propagated TM corresponding to the neighborhood pixels. Figure 8 shows the sum projection of selected foci at different defocus distances generated by the recovered TM with phase correction. This validates the algorithm of the TM retrieval with phase correction.

Fig. 8. Sum projection of selected foci measured at different defocus distances.

下载图片 查看所有图片

5 Discussion

The optimization problem in Eq. (3) is a phase-retrieval problem. The cost function of the phase-retrieval problem is formulated based on intensity difference, which is suitable for the assumption that the intensity measurements are polluted by Gaussian noise. With the assumption of Poisson noise, the cost function can be formulated with amplitude difference.39 Many algorithms have been proposed for the phase-retrieval problem, including gradient descent,40 Gerchberg–Saxton,41 Kalman filtering,42 L-BFGS,35^,43 modified Gauss Newton,35 Wirtinger flow,44 prVBEM,45 PhaseLift,46 reweighted amplitude flow,47 and PhaseMax.48 The L-BFGS method is a second-order optimization method, which was shown to converge faster than the first-order methods, such as gradient descent or Gerchberg–Saxton in phase retrieval from defocus images35 and Fourier ptychography.39 In this work, we used the intensity-based cost function and the L-BFGS method. A fair assessment of the formulation of the cost function and the optimal choice of the algorithm for the phase-retrieval problem in the TM retrieval is outside the scope of this work.

This work proposed to design the probing matrix Q (N×Nk) with the Fourier transform matrix. Using FFT, the computational complexity of the matrix–vector multiplication related to Q and QH reduces from Θ(NNk) to Θ(NlogNk). Here we give an example of the number of modulation modes Nk=8192 and the number of measurements N=65,536. The matrix Q has a size of 65,536×8192. The computational complexity reduces from Θ(65,536×8192) to Θ(65,536×13), and it is memory-efficient without storing Q. The computation related to the probing matrix Q is mostly inevitable in the algorithms of the phase-retrieval problem in TM retrieval. For example, gradient descent-based algorithms have to compute the cost function and gradient descent. The computational complexity of these algorithms is lower-bounded by Θ(NNk), due the matrix–vector multiplication related to Q. It is higher than that of our proposed method using FFT Θ(NlogNk). However, applying the similar FFT-based scheme in these algorithms could further reduce the computational complexity.

6 Conclusion

We have proposed a fast and phase-offset-error-free method for reference-less TM retrieval. By designing the probing incident complex fields with a Fourier transform matrix, the FFT-based TM retrieval algorithm achieves orders of magnitude of improvement in computational complexity [Θ(NlogNk)] versus [Θ(NNk)]. Further, the algorithm corrects the error of phase offset in the TM retrieval using the defocus intensity images. We have tested the proposed TM retrieval method by both simulations and experiments with MMF. It has been experimentally demonstrated 1200× speedup in recovering the TM of size 2286×8192 with 112.9 s for the MMF of 0.22 NA and 50μm diameter by the computer of 32 CPU cores. This work validated the method by evaluating 2D and 3D foci with the experimental setup using MMF. With the advantage of computational efficiency and the correction of phase offset, the method may be adapted to efficiently calibrate the TM of scattering media or imaging systems without reference for applications, such as diffusers,22 optical communication,49 3D holography displays,33 quantum networks,30^,31 optical computing system,28 and thin lens imaging system.32

7 Appendix A: Derivation of the First Derivative in the TM Retrieval

The optimization problem to recover one row of the TM is expressed as mintkf(tk)=‖Ik−|Qtk|2‖22.(16)

Next, we define F=Ik−|Qtk|2,(17)f(tk)=FHF,(18)where F is a vector. According to the chain rule, the first derivative of the cost function can be written as $$\begin{gathered} ∂f∂tk=−∂f∂F∂F∂tk \\ =−∂f∂F∂|Qtk|2∂tk \\ =−4FHdiag(conj(Qtk))Q. \end{gathered}$$(19)

Thus we have the Hermitian of the first derivative as $$\begin{gathered} ∂f∂tkH=−4QHdiag(Qtk)F \\ =−4QHdiag(Qtk)(Ik−|Qtk|2). \end{gathered}$$(20)

8 Appendix B: Defocus Propagation

According to the theory of angular spectrum propagation,50 the defocus propagation kernel in frequency domain is expressed as h(u,v,zd)=exp[j2πλ1−(λu)2−(λv)2zd]p(u,v),(21)where λ is the wavelength of the illumination, u and v are the spatial frequency coordinates, and p(u,v) is the pupil of the imaging system. The pupil is written as P(u,v)={1,λu2+v2≤NA,0,λu2+v2>NA.(22)

The vector h is raster-scanned from h(u,v,zd).

9 Appendix C: Derivation of the First Derivative in the Algorithm of Phase Correction

The optimization of solving the phase offset from the defocus intensity images is rewritten as minϕg(ϕ)=∑nd‖Ind−|Andejϕ|2‖22,(23)where And=K2HPdiag(h)K1diag(Testejθnd). Next, we define Gnd=Ind−|Andejϕ|2,(24)gnd=GndHGnd.(25)

Using the chain rule, we have $$\begin{gathered} ∂gnd∂ejϕ=−∂gnd∂Gnd∂Gnd∂ejϕ \\ =−∂gnd∂Gnd∂|Andejϕ|2∂ejϕ \\ =−4GndHdiag[conj(Andejϕ)]And. \end{gathered}$$(26)

We can have ∂ejϕ∂ϕ=diag(jejϕ).(27)

By combining Eqs. (26) and (27), we can get ∂gnd∂ϕ=real{−4GndHdiag[conj(Andejϕ)]Anddiag(jejϕ)}.(28)

It is easy to obtain ∂gndH∂ϕ=real[−4diag(−je−jϕ)AndHdiag(Andejϕ)⁢(Ind−|Andejϕ|2)].(29)

So, we have $$\begin{gathered} ∂gH∂ϕ=∑nd∂gndH∂ϕ \\ =∑ndreal[−4diag(−je−jϕ)AndHdiag(Andejϕ)⁢(Ind−|Andejϕ|2)]. \end{gathered}$$(30)

Jingshan Zhong is an associate research scientist at Zhejiang Lab, China. He received his BS degree in electronic science and technology from the University of Science and Technology of China, Hefei, China and his PhD in electrical and electronic engineering from Nanyang Technological University, Singapore, in 2010 and 2015, respectively. He got his postdoc training from the Computational Imaging Lab at UC Berkeley, advised by Prof. Laura Waller. His research interests include phase imaging, light-field imaging, imaging through scattering, signal processing, numerical optimization, and machine learning.

Zhong Wen obtained his BS degree from Dalian University of Technology in 2016. He is currently pursuing his PhD in optical engineering at Zhejiang University. His research interests include endoscopy imaging and computational imaging.

Quanzhi Li received his BS degree in electronic science and technology from Harbin Institute of Technology in 2021. He is currently pursuing his PhD in optical engineering at Zhejiang University. His research interests include multimode fiber imaging and computational imaging.

Qilin Deng is a graduate student at Zhejiang University. He completed his undergraduate studies at Jiangnan University, Wuxi, China, earning his BS degree with honors in 2020. His research interests focus on computational imaging, optics, and fiber imaging.

Qing Yang received her PhD from the College of Materials Science and Engineering, Zhejiang University, China, in 2006. She worked as a visiting scientist in the Department of Materials Science and Engineering, Georgia Institute of Technology, United States, from 2009 to 2012. She worked as a visiting scientist at the University of Cambridge, United Kingdom, in 2018. Currently, she is a professor at the College of Optical Science and Engineering of Zhejiang University. She is also the director of the Research Center for Humanoid Sensing, Zhejiang Lab, Hangzhou, China. Her research focuses on micro/nanophotonics, nanomaterials, and endoscopy imaging.