1. Introduction

Terahertz (THz) waves, which possess a frequency range spanning from 0.1 to 10 THz, will be used for information transmission in future communication technologies^[1,2]. Moreover, owing to their distinctive electromagnetic characteristics, these materials have also been extensively employed in spectral detection and nondestructive testing^[3,4]. In the last 20 years, significant attention has been directed into the development of functional devices operating in the THz frequency range, with the aim of generating and manipulating THz waves^[5]. Several methods have been proven for the generation of THz pulses, such as photoconductive antennas^[6], nonlinear crystals^[7], air plasma^[8], epsilon-near-zero (ENZ) materials^[9], and spintronics films^[10,11]. On the other hand, the manipulation of THz waves has been achieved by the utilization of artificial electromagnetic structures such as metamaterials^[12–14] and metasurfaces^[15–18], which have been adapted from different frequency bands. Metalenses^[19–21], metagratings^[22], and coding metasurfaces^[23] have been established with the purpose of exerting precise control over THz waves by manipulation techniques.

However, the commonly adopted THz lenses in current imaging and communication systems are still founded on the conventional design of a convex circular lens. Although metal and dielectric metalenses have been extensively utilized as high-gain transmitting antennas in the microwave and high-performance practicable systems in the optical bands^[24–27], respectively, there are a few obvious obstacles at THz band. In the microwave band, ohm loss in metal metasurfaces is typically negligible. However, in the THz range, it cannot be ignored and influences performance. In the meantime, THz dielectric metalenses are typically silicon-based and necessitate 100-µm-thick deep silicon etching^[28], a manufacturing challenge. Furthermore, the size of THz devices is typically around 10 mm, which is only approximately 10 times the wavelength. This means that the accuracy of performance prediction based solely on geometric optics design is also limited.

Recently, multilevel diffractive lenses, which can be treated as a kind of diffractive optical element (DOE), have been proven to have the same performance as metalenses^[29,30]. To achieve high performance, however, multiple phase levels and multiple depth levels are required, which significantly increases fabrication complexity and presents considerable obstacles if multiple pattern lithography is utilized.

Here, we propose an inverse design method to build a THz multilevel diffractive lens via three-dimensional (3D) printing to overcome this complexity. 3D printing, also known as additive manufacturing, has been extensively developed over the past decade due to its great potential for producing more customized devices^[31–33]. It refers to the process of creating 3D objects layer by layer from a computer-aided design (CAD) model, which is ideal for constructing multilevel diffractive lenses. It permits the precise fabrication of the numerous required layers, thereby allowing for greater flexibility in processing the height of the diffractive structure. By integrating vectorial electromagnetic simulation in a cylindrical coordinate system with particle swarm optimization (PSO) or differential evolution (DE), the printed structures can be optimized layer by layer. As shown in Fig. 1, compared with conventional Teflon lenses, the 3D-printed lens is lighter and smaller. In addition, the optical performance can be accurately predicted due to rigorous electromagnetic wave calculations.

Fig. 1. Lenses used in a THz communication system. (a) Conventional THz lens made by Teflon; (b) 3D printed THz multilevel lens.

下载图片 查看所有图片

2. Methodology

The flow of design and optimization is depicted in Fig. 2(a). Initial model input parameters (height profile) are derived from the theoretical calculations for the conventional Fresnel lens. For a lens intended for focusing, the phase profile should be arranged according to the equation, ϕML(x,y)=2πλ0(f−x2+y2+f2),(1)where λ0 is the design wavelength, x and y are the coordinates of each pixel, and f is the focal length. As for a multilevel lens, the height level should adhere to the equation, hML(r)=λ02π(n−1)ϕML(r),(2)where r=x2+y2, and n is the refractive index of the lens at the wavelength λ0.

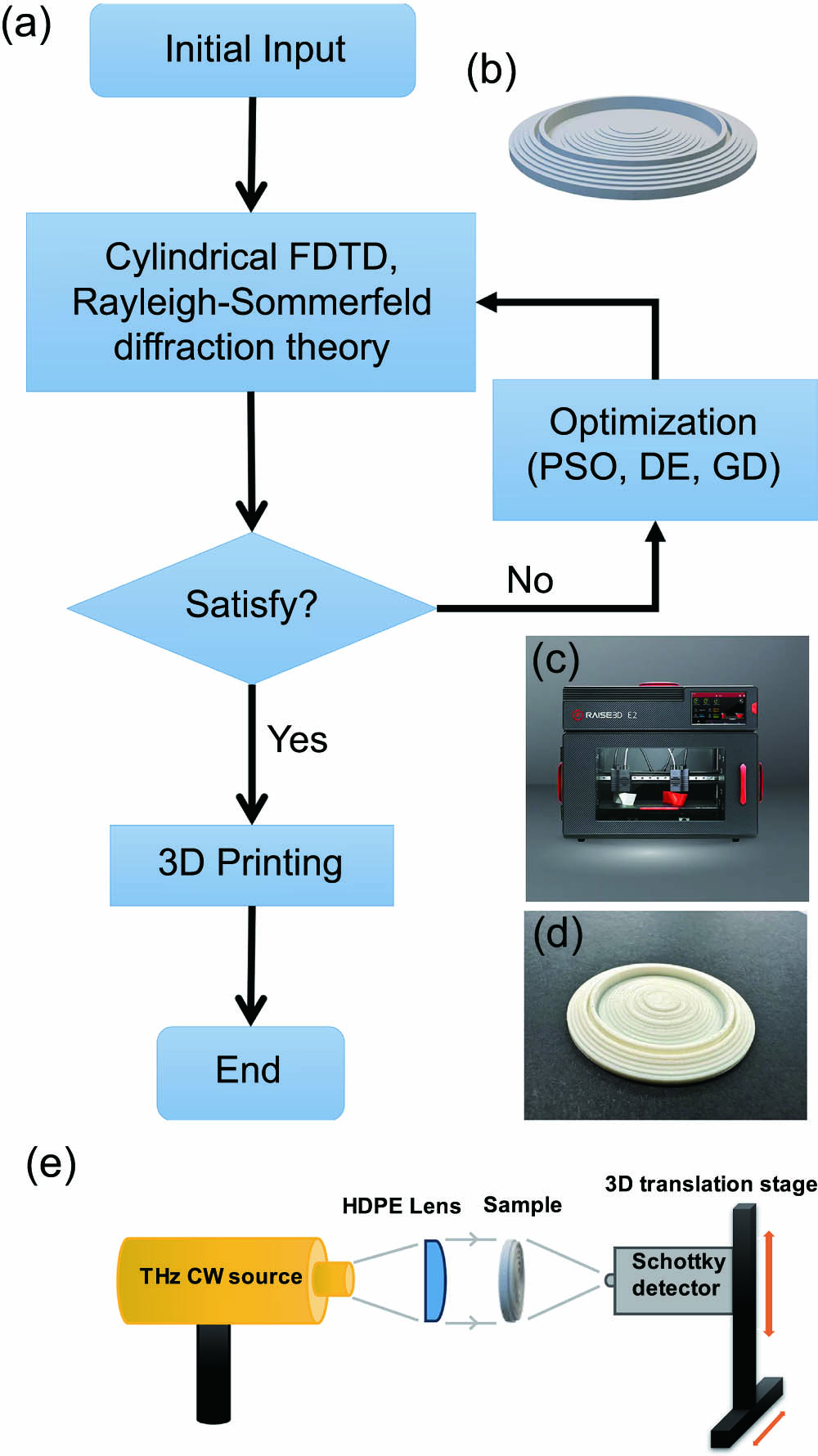
Fig. 2. Design, optimization, fabrication, and characterization process of 3D-printed THz multilevel diffractive lens. (a) Optimization flow; (b) multilevel lens profile designed using theoretical calculation; (c) 3D printer (RAISE3D N2) was used in the fabrication. (d) The multilevel diffractive lens is fabricated using 3D printing technology. (e) Configuration for focusing characterization experiments. PSO, particle swarm optimization; DE, differential evolution; GD, gradient descent.

下载图片 查看所有图片

A material of polylactic acid (PLA) was used for the 3D printed lens. Between 0.11 and 0.17 THz, PLA has a refractive index of approximately 1.57. The 3D printer (RAISE3D N2) has a resolution of 0.2 mm, so the height printing accuracy of the lenses is noted to be 0.2 mm. The accuracy of the x–y plane of the lenses was set to 1 mm. Consequently, the height profile is computed using Eqs. (1) and (2), slicing at this level of precision.

A finite-difference time-domain (FDTD) simulation is then used to examine the electric near-field distribution of the lens when THz waves pass through it. In order to reduce simulation time, a cylindrical FDTD method^[34] is introduced to simulate the lens due to its perfect central symmetry. Then, the far-field distribution is calculated using the Rayleigh–Sommerfeld diffraction theory, with inputs from the near field.

The Rayleigh–Sommerfeld diffraction theory can be used in an isotropic, homogeneous linear medium for light propagation and diffraction^[35,36]. With near-field data calculated by cylindrical FDTD, the far-field data could be solved along the direction of light propagation. We use the angular spectrum method to calculate the Rayleigh–Sommerfeld integral. The propagation of the light can be solved like A(α,β,z)=A(α,β,0)G(α,β,z),(3)where A(α,β,z) is the fast Fourier transformation (FFT) of the light field at a distance z along the propagation direction, and G(α,β,z)=ejk2−α2−β2z is the optical transfer function of the linear homogeneous isotropic medium. Using the cylindrical FDTD and Rayleigh–Sommerfeld diffraction theory, the simulation time for light propagation through a lens is reduced to a few seconds.

If the obtained performance satisfies the desired specifications for a multilevel lens, the design is deemed acceptable and can proceed to the fabrication stage using the 3D printer (RAISE3D N2) depicted in Fig. 2(c). However, if the performance does not satisfy the desired criteria, the design is optimized to achieve a satisfactory outcome. Multiple methods, such as DE, PSO, and gradient descent (GD), are used to optimize multilevel lenses. In different instances, the penalty function of optimization may assume various forms. For the case of a simple focusing lens at 0.14 THz, the penalty function is illustrated as follows: F(HML)=1−E2(0,f)∑r=−radiusradiusE2(r,f)−∑r=−radiusradiusE2(r,f)∑z=02f∑r=−radiusradiusE2(r,z),(4)where HML is a height array that indicates the height arrangement, E2(r,z) is the electric intensity distribution in the cylindrical coordinate, and f is the focal length aimed for.

In order to evaluate the performance of the fabricated lenses, a single-frequency radiation source operating at 0.14 THz (utilizing IMPATT diodes) was employed to illuminate the sample. The radiation was collimated using an HDPE lens, and the resulting field distribution after passing through the sample was measured using a Schottky detector. The Schottky detector was mounted on a 3D translation stage with a step size of 0.5 mm, as illustrated in Fig. 2(e).

3. Results

To showcase the design methodology, three different types of THz multilevel diffractive lenses have been designed and fabricated. A lens with a focal length of 100 mm and a frequency of 0.14 THz was designed to supplant the conventional lens in a communication system. Additionally, a 0.89 numerical aperture (NA) chromatic multilevel lens was designed for 0.14 THz. In addition, a multilevel achromatic lens in the WR-6.5 band (0.11–0.17 THz) was created.

3.1. Lens applied in THz communication system

As previously mentioned, 3D-printed THz multilevel diffractive lenses offer various advantages. Consequently, this section aims to demonstrate their potential to replace conventional lenses in THz communication systems. Figures 3(a) and 3(b) are the height level arrangements of the lens designed using Eq. (2) based on the 6-level phase and the optimized method with a 21-level phase, respectively. In Figs. 3(c) and 3(d), the simulated electric field distribution of two lenses at the focal length plane (x–y section) and r–z section was depicted. The optimized version features a higher electric field. Figures 3(e) and 3(f) depict the experimental outcomes, which correspond well to the simulation. To comprehensively assess the performance of the optimized lens, it is integrated into a self-built THz communication system for testing, replacing the traditional Teflon lens commonly used in such systems. The eye diagrams depicted in Figs. 3(i) and 3(j) demonstrate that the optimized lenses exhibit similar performance. Additionally, the bit error ratio (BER), illustrated in Fig. 3(g), is virtually identical and approaches zero for both types of lenses, while that of the 6-level phase lenses reaches above 10−5. This indicates that the optimized lenses achieve comparable and error-free communication capabilities.

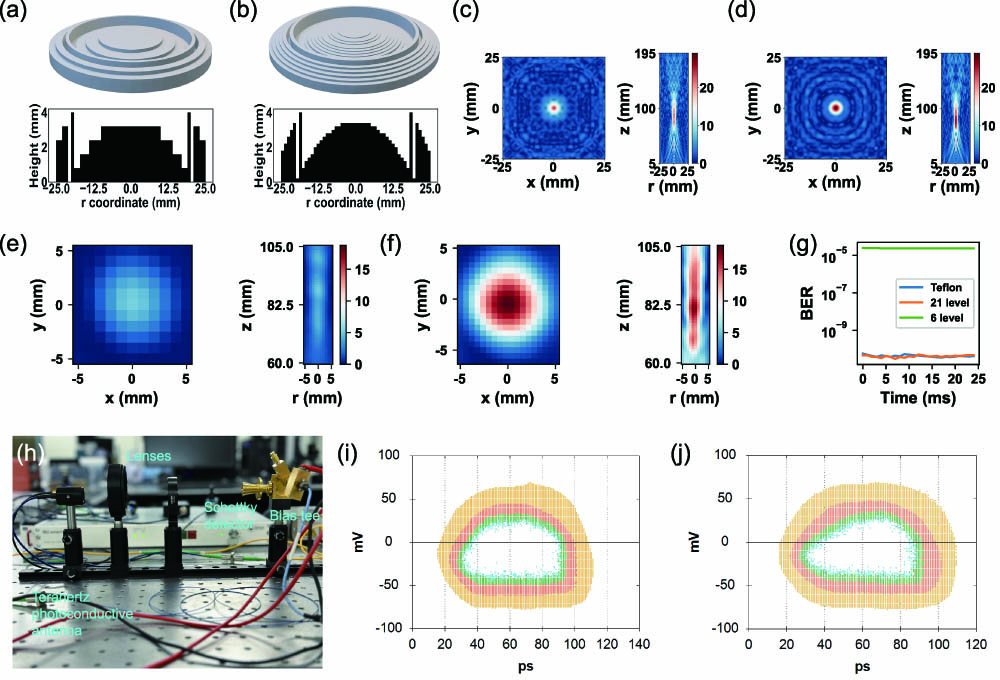
Fig. 3. Simulation and experiment results of THz lenses. (a), (b) Structures of the 6-level lens and 21-level lens, respectively; (c), (d) simulation results of the 6-level lens and 21-level lens, respectively; (e), (f) experiment results of the 6-level lens and 21-level lens, respectively; (g) BER tested through the THz communication system, comparing the performance of Teflon and two different multilevel 3D printed PLA lens; (h) picture of the THz communication system used; (i), (j) eye contour of the THz communication system using Teflon and 21-level 3D printed PLA lens, respectively.

下载图片 查看所有图片

3.2. High NA lenses

In the area of imaging applications, the significance of high NA lenses cannot be overstated, as they enable the capture of more intricate and higher-resolution information. The objective of this section is to provide evidence that 3D-printed THz multilevel diffractive lenses can achieve a high NA, making them well-suited for integration into advanced THz imaging systems. To this end, a high NA lens operating at a frequency of 0.14 THz was designed and fabricated using 3D printing technology. With a diameter of 40 mm and a focal length of 10 mm, the lens’s optimization function utilized in this study aligns with the one described in the methodology section, achieving an NA of approximately 0.9. Figure 4(a) depicts the designed height profile and the fabricated sample of the lens. The simulation results in Fig. 4(b) display the electric field distribution at the focal length plane (x–y section) and r–z section, affirming the lens’s exceptional focusing performance. The experimental outcomes of the lens can be observed in Fig. 4(c), which illustrates the electric field distribution at three different planes: z=9, 10, and 11 mm. Conversely, when utilizing the lens, the peak energy intensity increased to 0.016 at the z=9mm plane and further rose to 0.028 and 0.027 at the z=10 and 11 mm planes, respectively. Figures 4(d) and 4(e) showcase the profiles of the focal spots, providing visual evidence that the focal length of the fabricated sample aligns with the optimized design.

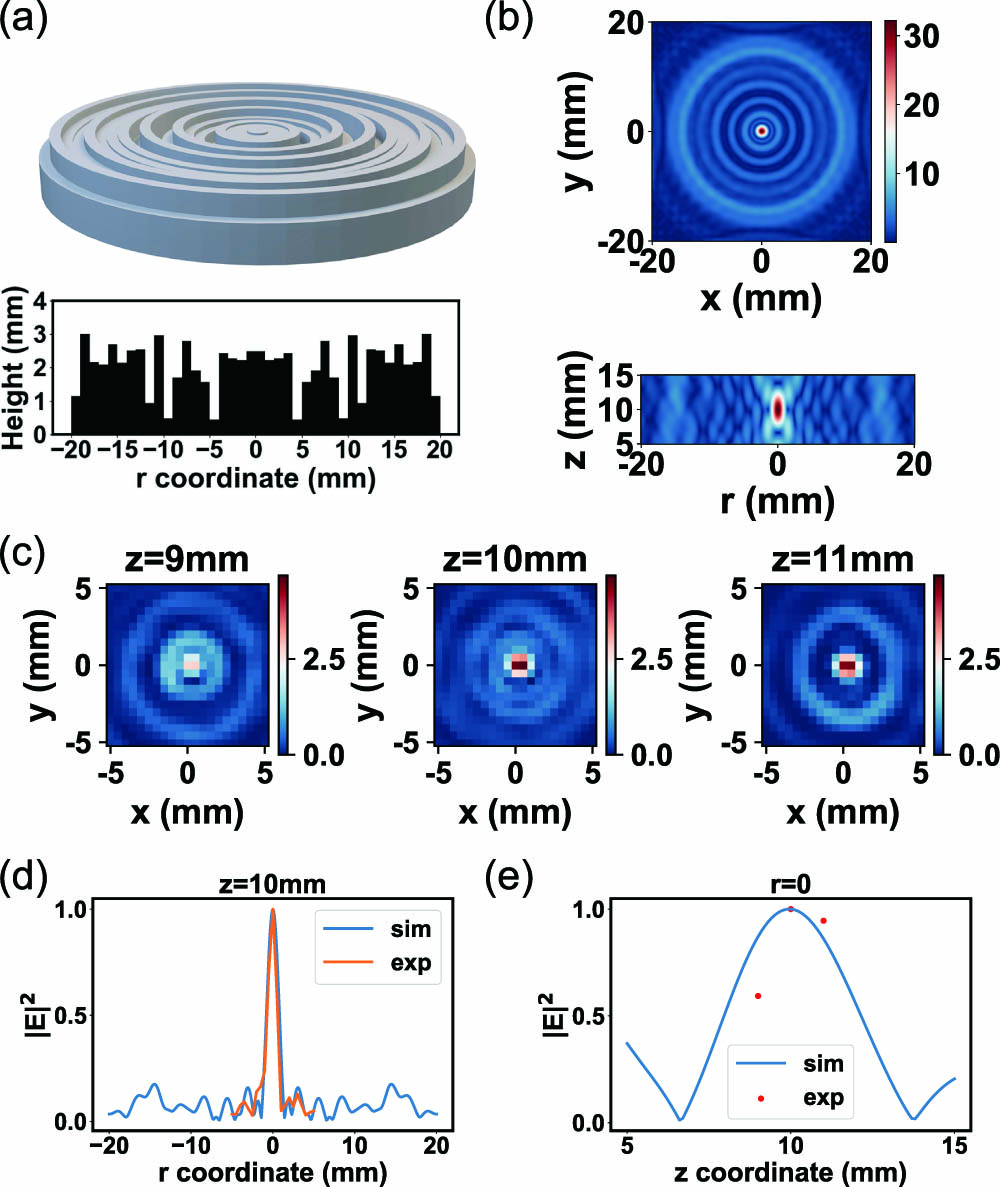
Fig. 4. Simulation and experiment results of high NA THz lens. (a) Structure of high NA THz multilevel lens; (b) power distribution of the lens on the x–y plane and r–z plane; (c) experiment results of multilevel lens received around focal length; (d), (e) illustration of simulation and experiment results along the r coordinate and z coordinate, respectively.

下载图片 查看所有图片

3.3. Achromatic lenses

In the current THz system, conventional convex lenses typically suffer from chromatic aberration. For instance, conducting a frequency mapping multiplexing experiment without an achromatic lens is challenging^[37]. However, in this section, we present theoretical evidence that 3D printed multilevel diffractive lenses have the potential to be achromatic. The penalty function isF(HML)=∑freq=0.11THz0.17THz(ffreq−f)2,(5)where freq is the frequency simulated, ffreq is the focal length under the specified frequency, and f is the focal length aimed for. The achromatic lens was optimized based on the high NA chromatic lens, with a diameter of 40 mm and a focal length of around 10 mm, ranging from 0.11 to 0.17 THz. As the simulation results show in Figs. 5(a) and 5(b), Fig. 5(a) displays the performance of high NA chromatic lens at 0.11 to 0.17 THz; meanwhile, Fig. 5(b) shows the high NA achromatic lens.

Fig. 5. Simulation results of THz chromatic and achromatic multilevel lens. (a), (b) Simulation results ranging from 0.11 to 0.17 THz of the chromatic and achromatic lens, respectively; (c) structure of the achromatic lens optimized; (d), (e) simulation results ranging from 0.11 to 0.17 THz on z coordinate of both chromatic and achromatic lens, respectively.

下载图片 查看所有图片

The structure of the achromatic lens is illustrated in Fig. 5(c), and the chromatic lens is the same as the lens in Fig. 4(b). Figure 5(d) shows the focal length of the chromatic lens shifting for different frequencies. The electric field distribution along the z coordinate of the achromatic lens ranging from 0.11 to 0.17 THz is also illustrated in Fig. 5(e), which shows a perfect achromatic focusing performance around the focal length of 10 mm.

4. Conclusion

The multilevel THz lens, fabricated using 3D printing technology, offers several notable advantages over conventional lenses. First, its thin structure allows for a compact and lightweight design, enabling efficient integration into THz imaging systems. Second, the fabrication process is relatively simple, using a common 3D printer, which makes production cost-effective and easily scalable. Additionally, the design process is quick and easy, saving valuable time in lens development. Furthermore, these lenses exhibit satisfactory performance, meeting the desired requirements and effectively fulfilling their intended functionality. Overall, the combination of these advantages makes 3D-printed multilevel THz lenses an appealing choice in terms of performance and cost-effectiveness. It is important to note that the method currently applies to the WR-6.5 band using fused deposition modeling with PLA. However, there is potential for scaling down the technology to operate in the optical band by utilizing two-photon polymerization technology.